5.3: Resolver sistemas de equações por eliminação

Objetivos de

Ao final desta seção, você poderá:

• Resolva um sistema de equações por eliminação
• Resolva aplicações de sistemas de equações por eliminação
• Escolha o método mais conveniente para resolver um sistema de equações lineares

Nota

Antes de começar, faça este teste de prontidão.

1. Simplifique −5 (6−3a).
   Se você perdeu esse problema, revise o Exercício 1.10.43.
2. Resolva a equação\(\frac{1}{3}x+\frac{5}{8}=\frac{31}{24}\).
   Se você perdeu esse problema, revise o Exercício 2.5.1.

Resolvemos sistemas de equações lineares por representação gráfica e por substituição. A representação gráfica funciona bem quando os coeficientes variáveis são pequenos e a solução tem valores inteiros. A substituição funciona bem quando podemos resolver facilmente uma equação para uma das variáveis e não ter muitas frações na expressão resultante.

O terceiro método de resolução de sistemas de equações lineares é chamado de Método de Eliminação. Quando resolvemos um sistema por substituição, começamos com duas equações e duas variáveis e o reduzimos a uma equação com uma variável. Isso também é o que faremos com o método de eliminação, mas teremos uma maneira diferente de chegar lá.

Resolva um sistema de equações por eliminação

O Método de Eliminação é baseado na Propriedade de Adição da Igualdade. A Propriedade de Adição da Igualdade diz que quando você adiciona a mesma quantidade aos dois lados de uma equação, você ainda tem igualdade. Estenderemos a Propriedade de Adição de Igualdade para dizer que quando você adiciona quantidades iguais aos dois lados de uma equação, os resultados são iguais.

Para qualquer expressão a, b, c e d,

\[\begin{array}{lc} \text{ if } & a=b \\ \text { and } & c=d \\ \text { then } &a+c =b+d \end{array}\]

Para resolver um sistema de equações por eliminação, começamos com as duas equações na forma padrão. Em seguida, decidimos qual variável será mais fácil de eliminar. Como podemos decidir? Queremos que os coeficientes de uma variável sejam opostos, para que possamos somar as equações e eliminar essa variável.

Observe como isso funciona quando adicionamos essas duas equações:

\[\begin{array}{l} 3x+y=5 \\ \underline{2x-y=0} \\ 5x\quad\quad=5\end{array}\]

Os y's somam a zero e temos uma equação com uma variável.

Vamos tentar outro:

\[\left\{\begin{array}{l}{x+4 y=2} \\ {2 x+5 y=-2}\end{array}\right.\]

Desta vez, não vemos uma variável que possa ser eliminada imediatamente se somarmos as equações.

Mas se multiplicarmos a primeira equação por −2, criaremos os coeficientes de x opostos. Devemos multiplicar cada termo em ambos os lados da equação por −2.

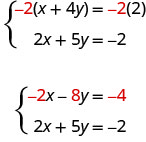
Agora vemos que os coeficientes dos termos x são opostos, então x será eliminado quando adicionarmos essas duas equações.

Adicione você mesmo as equações — o resultado deve ser −3 y = −6. E isso parece fácil de resolver, não é? Aqui está o que seria.

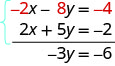
Faremos mais uma:

\[\left\{\begin{array}{l}{4 x-3 y=10} \\ {3 x+5 y=-7}\end{array}\right.\]

Não parece que possamos fazer com que os coeficientes de uma variável sejam opostos multiplicando uma das equações por uma constante, a menos que usemos frações. Então, em vez disso, teremos que multiplicar as duas equações por uma constante.

Podemos fazer com que os coeficientes de x sejam opostos se multiplicarmos a primeira equação por 3 e a segunda por −4, então obtemos 12 x e −12 x.

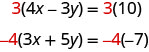
Isso nos dá essas duas novas equações:

\[\left\{\begin{aligned} 12 x-9 y &=30 \\-12 x-20 y &=28 \end{aligned}\right.\]

Quando adicionamos essas equações,

\[\[\left\{\begin{array}{r}{12 x-9 y=30} \\ {\underline{-12 x-20 y=28}} \\\end{array}\right.\\\quad\qquad {-29 y=58}\]\]

os x's são eliminados e temos apenas −29 y = 58.

Depois de obtermos uma equação com apenas uma variável, nós a resolvemos. Em seguida, substituímos esse valor em uma das equações originais para resolver a variável restante. E, como sempre, verificamos nossa resposta para garantir que seja uma solução para ambas as equações originais.

Agora veremos como usar a eliminação para resolver o mesmo sistema de equações que resolvemos por meio de gráficos e por substituição.

Exercício\(\PageIndex{1}\): How to Solve a System of Equations by Elimination

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)

Responda

Exercício\(\PageIndex{2}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x-3 y=7}\end{array}\right.\)

Responda

(2, −1)

Exercício\(\PageIndex{3}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{4 x+y=-5} \\ {-2 x-2 y=-2}\end{array}\right.\)

Responda

(−2,3)

As etapas estão listadas abaixo para facilitar a referência.

COMO RESOLVER UM SISTEMA DE EQUAÇÕES POR ELIMINAÇÃO.

1. Escreva as duas equações na forma padrão. Se algum coeficiente for fracionário, limpe-o.
2. Faça os coeficientes de uma variável oposta.
   • Decida qual variável você eliminará.
   • Multiplique uma ou ambas as equações para que os coeficientes dessa variável sejam opostos.
3. Adicione as equações resultantes da Etapa 2 para eliminar uma variável.
4. Resolva a variável restante.
5. Substitua a solução da Etapa 4 em uma das equações originais. Em seguida, resolva a outra variável.
6. Escreva a solução como um par ordenado.
7. Verifique se o par ordenado é uma solução para ambas as equações originais.

Primeiro, faremos um exemplo em que podemos eliminar uma variável imediatamente.

Exercício\(\PageIndex{4}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{x+y=10} \\ {x-y=12}\end{array}\right.\)

Responda

Ambas as equações estão na forma padrão.
Os coeficientes de y já são opostos.
Adicione as duas equações para eliminar y. A equação resultante tem apenas 1 variável, x.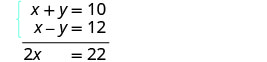
Resolva x, a variável restante. Substitua x = 11 em uma das equações originais.
Resolva para a outra variável, y.
Escreva a solução como um par ordenado.	O par ordenado é (11, −1).
Verifique se o par ordenado é uma solução para ambas as equações originais. \(\begin{array}{rllrll} x+y &=&10 &x-y&=&12\\ 11+(-1) &\stackrel{?}{=}&10 & 11-(-1) &\stackrel{?}{=}&12\\ 10 &=&10 \checkmark & 12 &=&12 \checkmark \end{array}\)
	A solução é (11, −1).

Exercício\(\PageIndex{5}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{2 x+y=5} \\ {x-y=4}\end{array}\right.\)

Responda

(3, −1)

Exercício\(\PageIndex{6}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{x+y=3} \\ {-2 x-y=-1}\end{array}\right.\)

Responda

(−2,5)

No Exercício\(\PageIndex{7}\), seremos capazes de fazer os coeficientes de uma variável oposta multiplicando uma equação por uma constante.

Exercício\(\PageIndex{7}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{3 x-2 y=-2} \\ {5 x-6 y=10}\end{array}\right.\)

Responda

Ambas as equações estão na forma padrão.
Nenhum dos coeficientes é oposto.
Podemos fazer os coeficientes de y opostos multiplicando a primeira equação por −3.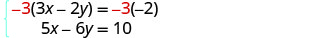
Simplifique.
Adicione as duas equações para eliminar y.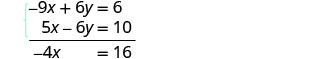
Resolva a variável restante, x. Substitua x = −4 em uma das equações originais.
Resolva para y.
Escreva a solução como um par ordenado.	O par ordenado é (−4, −5).
Verifique se o par ordenado é uma solução para ambas as equações originais. \(\begin{array}{rllrll} 3x-2y &=&-2 &5x-6y&=&10\\ 3(-4)-2(-5) &\stackrel{?}{=}&-2 & 5(-4)-6(-5) &\stackrel{?}{=}&10\\ -12+10&\stackrel{?}{=}&-2 &-20+30&\stackrel{?}{=}&10\\-2 &=&-2 \checkmark & 10 &=&10 \checkmark \end{array}\)
	A solução é (−4, −5).

Exercício\(\PageIndex{8}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{4 x-3 y=1} \\ {5 x-9 y=-4}\end{array}\right.\)

Responda

(1,1)

Exercício\(\PageIndex{9}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{3 x+2 y=2} \\ {6 x+5 y=8}\end{array}\right.\)

Responda

(−2,4)

Agora vamos fazer um exemplo em que precisamos multiplicar as duas equações por constantes para fazer com que os coeficientes de uma variável sejam opostos.

Exercício\(\PageIndex{10}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{4 x-3 y=9} \\ {7 x+2 y=-6}\end{array}\right.\)

Responda

Neste exemplo, não podemos multiplicar apenas uma equação por qualquer constante para obter coeficientes opostos. Portanto, multiplicaremos estrategicamente as duas equações por uma constante para obter os opostos.

Ambas as equações estão na forma padrão. Para obter coeficientes opostos de y, multiplicaremos a primeira equação por 2 e a segunda equação por 3.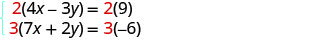
Simplifique.
Adicione as duas equações para eliminar y.
Resolva para x. Substitua x = 0 em uma das equações originais.
Resolva para y.
Escreva a solução como um par ordenado.	O par ordenado é (0, −3).
Verifique se o par ordenado é uma solução para ambas as equações originais. \(\begin{array}{rllrll} 4x-3y &=&9 &7x+2y&=&-6\\ 4(0)-3(-3) &\stackrel{?}{=}&9 & 7(0)+2(-3) &\stackrel{?}{=}&-6\\9 &=&9 \checkmark & -6 &=&-6 \checkmark \end{array}\)
	A solução é (0, −3).

Exercício\(\PageIndex{11}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right.\)

Responda

(1,3)

Exercício\(\PageIndex{12}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{7 x+8 y=4} \\ {3 x-5 y=27}\end{array}\right.\)

Responda

(4, −3)

Quando o sistema de equações contém frações, primeiro eliminaremos as frações multiplicando cada equação por seu LCD.

Exercício\(\PageIndex{13}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{x+\frac{1}{2} y=6} \\ {\frac{3}{2} x+\frac{2}{3} y=\frac{17}{2}}\end{array}\right.\)

Responda

Neste exemplo, ambas as equações têm frações. Nosso primeiro passo será multiplicar cada equação pelo LCD para limpar as frações.

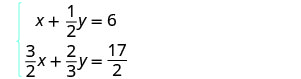
Para limpar as frações, multiplique cada equação pelo LCD.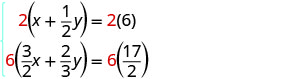
Simplifique.
Agora estamos prontos para eliminar uma das variáveis. Observe que ambas as equações estão na forma padrão.
Podemos eliminar y multiplicando a equação superior por −4.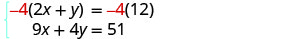
Simplifique e acrescente. Substitua x = 3 em uma das equações originais.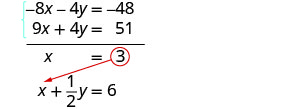
Resolva para y.
Escreva a solução como um par ordenado.	O par pedido é (3, 6).
Verifique se o par ordenado é uma solução para ambas as equações originais. \(\begin{array}{rllrll} x+\frac{1}{2}y &=&6 &\frac{3}{2}x+\frac{2}{3}y&=&\frac{17}{2}\\ 3+\frac{1}{2}(6) &\stackrel{?}{=}&6 &\frac{3}{2}(3) + \frac{2}{3}(6)&\stackrel{?}{=}&\frac{17}{2}\\ 3 + 3 &\stackrel{?}{=}&6 & \frac{9}{2 }+4 &\stackrel{?}{=} & \frac{17}{2}\\ 6 &=&6 \checkmark & \frac{9}{2} + \frac{8}{2} &\stackrel{?}{=} & \frac{17}{2}\\ && & \frac{17}{2} &=&\frac{17}{2} \checkmark \end{array}\)
	A solução é (3, 6).

Exercício\(\PageIndex{14}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{\frac{1}{3} x-\frac{1}{2} y=1} \\ {\frac{3}{4} x-y=\frac{5}{2}}\end{array}\right.\)

Responda

(6,2)

Exercício\(\PageIndex{15}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{x+\frac{3}{5} y=-\frac{1}{5}} \\ {-\frac{1}{2} x-\frac{2}{3} y=\frac{5}{6}}\end{array}\right.\)

Responda

(1, −2)

Nos Sistemas de Equações por Representação Gráfica, vimos que nem todos os sistemas de equações lineares têm um único par ordenado como solução. Quando as duas equações eram realmente a mesma reta, havia infinitas soluções. Chamamos isso de sistema consistente. Quando as duas equações descreveram retas paralelas, não havia solução. Chamamos isso de sistema inconsistente.

Exercício\(\PageIndex{16}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{3 x+4 y=12} \\ {y=3-\frac{3}{4} x}\end{array}\right.\)

Responda

\(\begin{array} {ll} & \left\{\begin{aligned} 3 x+4 y &=12 \\ y &=3-\frac{3}{4} x \end{aligned}\right. \\\\\text{Write the second equation in standard form.} & \left\{\begin{array}{l}{3 x+4 y=12} \\ {\frac{3}{4} x+y=3}\end{array}\right.\\ \\ \text{Clear the fractions by multiplying thesecond equation by 4.} & \left\{\begin{aligned} 3 x+4 y &=12 \\ 4\left(\frac{3}{4} x+y\right) &=4(3) \end{aligned}\right. \\\\ \text{Simplify.} & \left\{\begin{array}{l}{3 x+4 y=12} \\ {3 x+4 y=12}\end{array}\right.\\\\ \text{To eliminate a variable, we multiply thesecond equation by −1.} & \left\{\begin{array}{c}{3 x+4 y=12} \\ \underline{-3 x-4 y=-12} \end{array}\right.\\ &\qquad\qquad\quad 0=0 \\ \text{Simplify and add.} \end{array}\)

Essa é uma afirmação verdadeira. As equações são consistentes, mas dependentes. Seus gráficos seriam a mesma linha. O sistema tem infinitas soluções.

Depois de limparmos as frações na segunda equação, você notou que as duas equações eram iguais? Isso significa que temos linhas coincidentes.

Exercício\(\PageIndex{17}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{5 x-3 y=15} \\ {y=-5+\frac{5}{3} x}\end{array}\right.\)

Responda

infinitas soluções

Exercício\(\PageIndex{18}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{x+2 y=6} \\ {y=-\frac{1}{2} x+3}\end{array}\right.\)

Responda

infinitas soluções

Exercício\(\PageIndex{19}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{-6 x+15 y=10} \\ {2 x-5 y=-5}\end{array}\right.\)

Responda

\(\begin{array} {ll} \text{The equations are in standard form.}& \left\{\begin{aligned}-6 x+15 y &=10 \\ 2 x-5 y &=-5 \end{aligned}\right. \\\\ \text{Multiply the second equation by 3 to eliminate a variable.} & \left\{\begin{array}{l}{-6 x+15 y=10} \\ {3(2 x-5 y)=3(-5)}\end{array}\right. \\\\ \text{Simplify and add.} & \left\{\begin{aligned}{-6 x+15 y =10} \\ \underline{6 x-15 y =-15} \end{aligned}\right. \\ & \qquad \qquad \quad0\neq 5 \end{array}\)

Essa afirmação é falsa. As equações são inconsistentes e, portanto, seus gráficos seriam linhas paralelas.

O sistema não tem uma solução.

Exercício\(\PageIndex{20}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{-3 x+2 y=8} \\ {9 x-6 y=13}\end{array}\right.\)

Responda

sem solução

Exercício\(\PageIndex{21}\)

Resolva o sistema por eliminação. \(\left\{\begin{array}{l}{7 x-3 y=-2} \\ {-14 x+6 y=8}\end{array}\right.\)

Responda

sem solução

Resolva aplicações de sistemas de equações por eliminação

Alguns problemas de aplicação se traduzem diretamente em equações na forma padrão, então usaremos o método de eliminação para resolvê-los. Como antes, usamos nossa Estratégia de Solução de Problemas para nos ajudar a manter o foco e a organização.

Exercício\(\PageIndex{22}\)

A soma de dois números é 39. A diferença deles é 9. Encontre os números.

Responda

\(\begin{array} {ll} \textbf{Step 1. Read}\text{ the problem}& \\ \textbf{Step 2. Identify} \text{ what we are looking for.} & \text{We are looking for two numbers.} \\\textbf{Step 3. Name} \text{ what we are looking for.} & \text{Let n = the first number.} \\ & \text{ m = the second number} \\\textbf{Step 4. Translate} \text{ into a system of equations.}& \\ & \text{The sum of two numbers is 39.} \\ & n+m=39\\ & \text{Their difference is 9.} \\ & n−m=9 \\ \\ \text{The system is:} & \left\{\begin{array}{l}{n+m=39} \\ {n-m=9}\end{array}\right. \\\\ \textbf{Step 5. Solve} \text{ the system of equations. } & \\ \text{To solve the system of equations, use} \\ \text{elimination. The equations are in standard} \\ \text{form and the coefficients of m are} & \\ \text{opposites. Add.} & \left\{\begin{array}{l}{n+m=39} \\ \underline{n-m=9}\end{array}\right. \\ &\quad 2n\qquad=48 \\ \\\text{Solve for n.} & n=24 \\ \\ \text{Substitute n=24 into one of the original} &n+m=39 \\ \text{equations and solve form.} & 24+m=39 \\ & m=15 \\ \textbf{Step 6. Check}\text{ the answer.} & \text{Since 24+15=39 and 24−15=9, the answers check.}\\ \textbf{Step 7. Answer} \text{ the question.} & \text{The numbers are 24 and 15.} \end{array}\)

Exercício\(\PageIndex{23}\)

A soma de dois números é 42. A diferença deles é 8. Encontre os números.

Responda

Os números são 25 e 17.

Exercício\(\PageIndex{24}\)

A soma de dois números é −15. A diferença deles é −35. Encontre os números.

Responda

Os números são −25 e 10.

Exercício\(\PageIndex{25}\)

Joe para em uma lanchonete todos os dias a caminho do trabalho. Na segunda-feira, ele comeu um pedido de batatas fritas médias e dois refrigerantes pequenos, que tinham um total de 620 calorias. Terça-feira, ele comeu dois pedidos de batatas fritas médias e um refrigerante pequeno, totalizando 820 calorias. Quantas calorias existem em uma ordem de batatas fritas médias? Quantas calorias em um pequeno refrigerante?

Responda

Etapa 1. Leia o problema.
Etapa 2. Identifique o que estamos procurando.	Estamos procurando o número de calorias em uma ordem de batatas fritas médias e em um pequeno refrigerante.
Etapa 3. Diga o que estamos procurando.	Seja f = o número de calorias em 1 ordem de batatas fritas médias. s = o número de calorias em 1 refrigerante pequeno.
Etapa 4. Traduza em um sistema de equações:	uma batata frita média e dois refrigerantes pequenos tinham um total de 620 calorias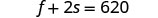
	duas batatas fritas médias e um refrigerante pequeno tinham um total de 820 calorias.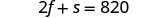
Nosso sistema é: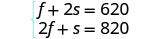
Etapa 5. Resolva o sistema de equações. Para resolver o sistema de equações, use a eliminação. As equações estão na forma padrão. Para obter coeficientes opostos de f, multiplique a equação superior por −2.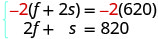
Simplifique e acrescente.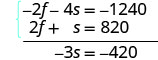
Resolva por s.
Substitua s = 140 em uma das equações originais e resolva f.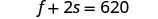
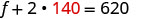
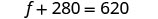
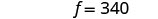
Etapa 6. Verifique a resposta.	Verifique se esses números fazem sentido no problema e se são soluções para ambas as equações. Deixamos isso para você!
Etapa 7. Responda à pergunta.	O refrigerante pequeno tem 140 calorias e as batatas fritas 340 calorias.

Exercício\(\PageIndex{26}\)

Malik para no supermercado para comprar um saco de fraldas e 2 latas de fórmula. Ele gasta um total de $37. Na semana seguinte, ele para e compra 2 sacos de fraldas e 5 latas de fórmula por um total de $87. Quanto custa um saco de fraldas? Quanto custa uma lata de fórmula?

Responda

O saco de fraldas custa $11 e a lata de fórmula custa $13.

Exercício\(\PageIndex{27}\)

Para obter sua ingestão diária de frutas durante o dia, Sasha come uma banana e 8 morangos na quarta-feira para uma contagem de calorias de 145. Na quarta-feira seguinte, ela come duas bananas e 5 morangos, totalizando 235 calorias para a fruta. Quantas calorias existem em uma banana? Quantas calorias tem um morango?

Responda

Há 105 calorias em uma banana e 5 calorias em um morango.

Escolha o método mais conveniente para resolver um sistema de equações lineares

Quando você tiver que resolver um sistema de equações lineares em uma aula de matemática posterior, geralmente não será informado sobre qual método usar. Você precisará tomar essa decisão sozinho. Então, você deve escolher o método mais fácil de fazer e minimizar suas chances de cometer erros.

Exercício\(\PageIndex{28}\)

Para cada sistema de equações lineares, decida se seria mais conveniente resolvê-lo por substituição ou eliminação. Explique sua resposta.

1. \(\left\{\begin{array}{l}{3 x+8 y=40} \\ {7 x-4 y=-32}\end{array}\right.\)
2. \(\left\{\begin{array}{l}{5 x+6 y=12} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)

Responda

1. \(\left\{\begin{array}{l}{3 x+8 y=40} \\ {7 x-4 y=-32}\end{array}\right.\)

Como as duas equações estão na forma padrão, usar a eliminação será mais conveniente.

2. \(\left\{\begin{array}{l}{5 x+6 y=12} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)

Como uma equação já foi resolvida para y, usar a substituição será mais conveniente.

Exercício\(\PageIndex{29}\)

Para cada sistema de equações lineares, decida se seria mais conveniente resolvê-lo por substituição ou eliminação. Explique sua resposta.

1. \(\left\{\begin{array}{l}{4 x-5 y=-32} \\ {3 x+2 y=-1}\end{array}\right.\)
2. \(\left\{\begin{array}{l}{x=2 y-1} \\ {3 x-5 y=-7}\end{array}\right.\)

Responda

1. Como as duas equações estão na forma padrão, usar a eliminação será mais conveniente.
2. Como uma equação já foi resolvida para xx, usar a substituição será mais conveniente.

Exercício\(\PageIndex{30}\)

Para cada sistema de equações lineares, decida se seria mais conveniente resolvê-lo por substituição ou eliminação. Explique sua resposta.

1. \(\left\{\begin{array}{l}{y=2 x-1} \\ {3 x-4 y=-6}\end{array}\right.\)
2. \(\left\{\begin{array}{l}{6 x-2 y=12} \\ {3 x+7 y=-13}\end{array}\right.\)

Responda

1. Como uma equação já está resolvida para yy, usar a substituição será mais conveniente;
2. Como as duas equações estão na forma padrão, usar a eliminação será mais conveniente.

Nota

Acesse esses recursos on-line para obter instruções e práticas adicionais com a resolução de sistemas de equações lineares por eliminação.

• Sistemas instrucionais de equações de resolução de vídeo por eliminação
• Resolução instrucional de vídeos por eliminação
• Sistemas instrucionais de resolução de vídeo por eliminação

Conceitos-chave

• Para resolver um sistema de equações por eliminação
  1. Escreva as duas equações na forma padrão. Se algum coeficiente for fracionário, limpe-o.
  2. Faça os coeficientes de uma variável oposta.
     • Decida qual variável você eliminará.
     • Multiplique uma ou ambas as equações para que os coeficientes dessa variável sejam opostos.
  3. Adicione as equações resultantes da Etapa 2 para eliminar uma variável.
  4. Resolva a variável restante.
  5. Substitua a solução da Etapa 4 em uma das equações originais. Em seguida, resolva a outra variável.
  6. Escreva a solução como um par ordenado.
  7. Verifique se o par ordenado é uma solução para ambas as equações originais.