1.11: Sistemas de medição
- Page ID
- 184462
Ao final desta seção, você poderá:
- Faça conversões de unidades no sistema dos EUA
- Use unidades de medida mistas no sistema dos EUA
- Faça conversões de unidades no sistema métrico
- Use unidades de medida mistas no sistema métrico
- Converta entre os sistemas métricos de medição dos EUA e os sistemas métricos
- Conversão entre temperaturas em Fahrenheit e Celsius
Uma introdução mais completa aos tópicos abordados nesta seção pode ser encontrada no capítulo Pré-álgebra, As propriedades dos números reais.
Faça conversões de unidades no sistema dos EUA
Existem dois sistemas de medição comumente usados em todo o mundo. A maioria dos países usa o sistema métrico. Os EUA usam um sistema de medição diferente, geralmente chamado de sistema dos EUA. Examinaremos primeiro o sistema dos EUA.
O sistema de medição dos EUA usa unidades de polegada, pé, jarda e milha para medir o comprimento e libra e tonelada para medir o peso. Para capacidade, as unidades usadas são xícara, caneca, litro e galões. Tanto o sistema americano quanto o sistema métrico medem o tempo em segundos, minutos e horas.
As equivalências das medidas são mostradas na Tabela\(\PageIndex{1}\). A tabela também mostra, entre parênteses, as abreviações comuns para cada medição.
| Sistema de Medição dos EUA | |
|---|---|
| \(\begin{array} {llll} {} &{\text{1 foot (ft.)}} &{=} &{\text{12 inches (in.)}} \\ {\textbf{Length}} &{\text{1 yard (yd.)}} &{=} &{\text{3 feet (ft.)}} \\ {} &{\text{1 mile (mi.)}} &{=} &{\text{5280 feet (ft.)}} \end{array}\) | \(\begin{array} {llll} {} &{\text{3 teaspoons (t)}} &{=} &{\text{1 tablespoon (T)}} \\ {} &{\text{16 tablespoons (T)}} &{=} &{\text{1 cup (C)}} \\ {} &{\text{1 cup (C)}} &{=} &{\text{8 fluid ounces (fl.oz.)}} \\ {\textbf{Volume}} &{\text{1 pint (pt.)}} &{=} &{\text{2 cups (C)}} \\ {} &{\text{1 quart (qt.)}} &{=} &{\text{2 pints (ft.)}} \\ {} &{\text{1 gallon (gal)}} &{=} &{\text{4 quarts (qt.)}} \end{array}\) |
|
\(\begin{array} {llll} {\textbf{Weight}} &{\text{1 pound (lb.)}} &{=} &{\text{16 ounces (oz.)}} \\ {} &{\text{1 ton}} &{=} &{\text{2000 pounds (lb.)}} \end{array}\) |
\(\begin{array} {llll} {} &{\text{1 minute (min)}} &{=} &{\text{60 seconds (sec)}} \\ {} &{\text{1 hour (hr)}} &{=} &{\text{60 minutes (min)}} \\ {\textbf{Time}} &{\text{1 day}} &{=} &{\text{24 hours (hr)}} \\ {} &{\text{1 week (wk)}} &{=} &{\text{7 days}} \\ {} &{\text{1 year (yr)}} &{=} &{\text{365 days}} \end{array}\) |
Em muitas aplicações reais, precisamos converter entre unidades de medida, como pés e jardas, minutos e segundos, quartos e galões, etc. Usaremos a propriedade de identidade da multiplicação para fazer essas conversões. Vamos reafirmar a propriedade de identidade da multiplicação aqui para facilitar a referência.
\(\begin{array} { l l } { \text {For any real number } a : } & { a \cdot 1 = a \quad 1 \cdot a = a } \\ { \textbf{1} \text { is the } \textbf{multiplicative identity } } \end{array}\)
Para usar a propriedade de identidade da multiplicação, escrevemos 1 em um formulário que nos ajudará a converter as unidades. Por exemplo, suponha que desejemos mudar polegadas para pés. Sabemos que 1 pé é igual a 12 polegadas, então escreveremos 1 como a fração\(\frac{\text{1 foot}}{\text{12 inches}}\). Quando multiplicamos por essa fração, não alteramos o valor, apenas alteramos as unidades.
Mas\(\frac{\text{12 inches}}{\text{1 foot}}\) também é igual a 1. Como decidimos se devemos multiplicar por\(\frac{\text{1 foot}}{\text{12 inches}}\) ou\(\frac{\text{12 inches}}{\text{1 foot}}\)? Escolhemos a fração que fará com que as unidades que queremos converter se dividam. Trate as palavras unitárias como fatores e “divida” as unidades comuns como fazemos com fatores comuns. Se quisermos converter 6666 polegadas em pés, qual multiplicação eliminará as polegadas?

As polegadas se dividem e deixam apenas pés. O segundo formulário não tem nenhuma unidade que se dividirá e, portanto, não nos ajudará.
Mary Anne tem 66 polegadas de altura. Converta a altura dela em pés.
- Responda
-




Lexie tem 30 polegadas de altura. Converta a altura dela em pés.
- Resposta
-
2,5 pés
Rene comprou uma mangueira de 18 metros de comprimento. Converta o comprimento em pés.
- Resposta
-
54 pés
- Multiplique a medida a ser convertida por 1; escreva 1 como uma fração relacionando as unidades dadas e as unidades necessárias.
- Multiplique.
- Simplifique a fração.
- Simplifique.
Quando usamos a propriedade de identidade da multiplicação para converter unidades, precisamos ter certeza de que as unidades das quais queremos mudar se dividirão. Normalmente, isso significa que queremos que a fração de conversão tenha essas unidades no denominador.
Ndula, um elefante no San Diego Safari Park, pesa quase 3,2 toneladas. Converta o peso dela em libras.
- Resposta
-
Vamos converter 3,2 toneladas em libras. Usaremos a propriedade de identidade da multiplicação, escrevendo 1 como a fração\(\frac{\text{2000 pounds}}{\text{1 ton}}\).
\(\text{3.2 tons}\) Multiplique a medida a ser convertida por 1. \(\text{3.2 tons} \cdot 1\) Escreva 1 como uma fração relacionada a toneladas e libras. \(\text{3.2 tons} \cdot \frac{\text{2000 pounds}}{\text{1 ton}}\) Simplifique. 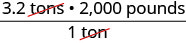
Multiplique. 6400 libras Ndula pesa quase 6400 libras.
O SUV de Arnold pesa cerca de 4,3 toneladas. Converta o peso em libras.
- Resposta
-
8600 libras
O navio de cruzeiro Carnival Destiny pesa 51000 toneladas. Converta o peso em libras.
- Resposta
-
102000000 libras
Às vezes, para converter de uma unidade para outra, podemos precisar usar várias outras unidades intermediárias, então precisaremos multiplicar várias frações.
Juliet vai com sua família para sua casa de verão. Ela ficará longe do namorado por 9 semanas. Converta o tempo em minutos.
- Resposta
-
Para converter semanas em minutos, converteremos semanas em dias, dias em horas e, em seguida, horas em minutos. Para fazer isso, multiplicaremos por fatores de conversão de 1.
9 semanas Escreva 1 como\(\frac{\text{7 days}}{\text{1 week}}\),\(\frac{\text{60 minutes}}{\text{1 hour}}\) e. \(\frac{\text{9 wk}}{\text{1}}\cdot\frac{\text{7 days}}{\text{1 wk}}\cdot\frac{\text{24 hr}}{\text{1 day}}\cdot\frac{\text{60 min}}{\text{1 hr}}\) Divida as unidades comuns. 
Multiplique. \(\frac{9\cdot7\cdot24\cdot60\text{ min}}{1\cdot1\cdot1\cdot1}\) Multiplique. 90.720 minutos Juliet e seu namorado ficarão separados por 90.720 minutos (embora possa parecer uma eternidade!).
A distância entre a Terra e a Lua é de cerca de 250.000 milhas. Converta esse comprimento em jardas.
- Resposta
-
440.000.000 jardas
Os astronautas da Expedição 28 na Estação Espacial Internacional passam 15 semanas no espaço. Converta o tempo em minutos.
- Resposta
-
151.200 minutos
Quantas onças estão em 1 galão?
- Resposta
-
Vamos converter galões em onças multiplicando por vários fatores de conversão. Consulte a tabela\(\PageIndex{1}\).
1 galão Multiplique a medida a ser convertida por 1. \(\frac{\text{1 gallon}}{\text{1}} \cdot \frac{\text{4 quarts}}{\text{1 gallon}} \cdot \frac{\text{2 pints}}{\text{1 quart}} \cdot \frac{\text{2 cups}}{\text{1 pint}} \cdot \frac{\text{8 ounces}}{\text{1 cup}}\) Use fatores de conversão para chegar à unidade certa.
Simplifique.
Multiplique. \(\frac{1\cdot 4\cdot 2\cdot 2\cdot 8\text{ ounces}}{1\cdot 1\cdot 1\cdot 1\cdot 1 }\) Simplifique. 128 onças
Quantas xícaras existem em 1 galão?
- Resposta
-
16 xícaras
Quantas colheres de chá há em 1 xícara?
- Resposta
-
48 colheres de chá
Use unidades de medida mistas no sistema dos EUA
Costumamos usar unidades de medida mistas em situações cotidianas. Suponha que Joe tenha 5 pés e 10 polegadas de altura, permaneça no trabalho por 7 horas e 45 minutos e depois coma um bife de 1 libra e 2 onças no jantar - todas essas medidas têm unidades mistas.
A realização de operações aritméticas em medições com unidades de medidas mistas requer cuidado. Certifique-se de adicionar ou subtrair unidades semelhantes!
Seymour comprou três bifes para um churrasco. Seus pesos eram 14 onças, 1 libra 2 onças e 1 libra 6 onças. Quantos quilos totais de bife ele comprou?
- Resposta
-
Adicionaremos os pesos dos bifes para encontrar o peso total dos bifes.
Adicione as onças. Em seguida, adicione os quilos. 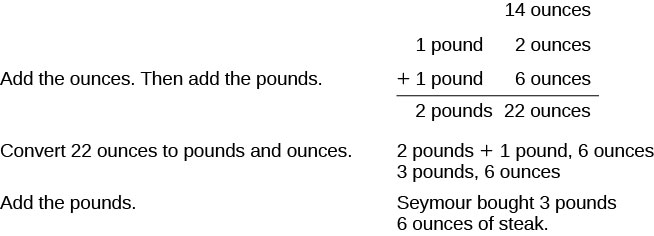
Converta 22 onças em libras e onças. 2 libras + 1 libra, 6 onças Adicione as libras. 3 libras, 6 onças Seymour comprou 3 libras e 6 onças de bife.
Laura deu à luz trigêmeos pesando 3 libras 3 onças, 3 libras 3 onças e 2 libras 9 onças. Qual foi o peso total ao nascer dos três bebês?
- Resposta
-
8 libras. 15 onças
Stan cortou duas peças de moldura de coroa para o quarto de sua família que tinham 8 pés 7 polegadas e 12 pés 11 polegadas. Qual foi o comprimento total da moldagem?
- Resposta
-
21 pés e 6 pol.
Anthony comprou quatro tábuas de madeira, cada uma com 6 pés e 4 polegadas de comprimento. Qual é o comprimento total da madeira que ele comprou?
- Resposta
-
Multiplicaremos o comprimento de uma prancha para encontrar o comprimento total.
Multiplique as polegadas e depois os pés. 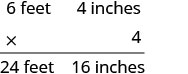
Converta as 16 polegadas em pés.
Adicione os pés.
Anthony comprou 25 pés e 4 polegadas de madeira.
Henri quer triplicar sua receita de molho de espaguete que usa 1 libra e 8 onças de perú moído. Quantos quilos de perú moído ele precisará?
- Resposta
-
4 libras. 8 onças.
Joellen quer dobrar uma solução de 5 galões e 3 litros. Quantos galões de solução ela terá ao todo?
- Resposta
-
11 galões 2 qt.
Faça conversões de unidades no sistema métrico
No sistema métrico, as unidades são relacionadas por potências de 10. As palavras da raiz de seus nomes refletem essa relação. Por exemplo, a unidade básica para medir o comprimento é um metro. Um quilômetro equivale a 1.000 metros; o prefixo quilo significa mil. Um centímetro é\(\frac{1}{100}\) de um metro, assim como um centavo é\(\frac{1}{100}\) de um dólar.
As equivalências das medidas no sistema métrico são mostradas na Tabela\(\PageIndex{2}\). As abreviações comuns para cada medição são fornecidas entre parênteses.
| Sistema Métrico de Medição | ||
|---|---|---|
| Comprimento | Missa | Capacidade |
| 1 quilômetro (km) = 1.000 m 1 hectômetro (hm) = 100 m 1 decâmetro (barragem) = 10 m 1 metro (m) = 1 m 1 decímetro (dm) = 0,1 m 1 centímetro (cm) = 0,01 m 1 milímetro (mm) = 0,001 m |
1 quilograma (kg) = 1.000 g 1 hectograma (hg) = 100 g 1 dekagram (dag) = 10 g 1 grama (g) = 1 g 1 decigrama (dg) = 0,1 g 1 centigrama (cg) = 0,01 g 1 miligrama (mg) = 0,001 g |
1 quilolitro (kL) = 1.000 L 1 hectolitro (hL) = 100 L 1 decalitro (DaL) = 10 L 1 litro (L) = 1 L 1 decilitro (dL) = 0,1 L 1 centilitro (cL) = 0,01 L 1 mililitro (mL) = 0,001 L |
| 1 metro = 100 centímetros 1 metro = 1.000 milímetros |
1 grama = 100 centigramas 1 grama = 1.000 miligramas |
1 litro = 100 centilitros 1 litro = 1.000 mililitros |
Para fazer conversões no sistema métrico, usaremos a mesma técnica que usamos no sistema dos EUA. Usando a propriedade de identidade da multiplicação, multiplicaremos por um fator de conversão de um para chegar às unidades corretas.
Você já correu uma corrida de 5K ou 10K? A duração dessas corridas é medida em quilômetros. O sistema métrico é comumente usado nos Estados Unidos quando se fala sobre a duração de uma corrida.
Nick correu uma corrida de 10 km. Quantos metros ele correu?
- Resposta
-
Vamos converter quilômetros em metros usando a propriedade de identidade da multiplicação.
10 quilômetros Multiplique a medida a ser convertida por 1. 
Escreva 1 como uma fração relacionada a quilômetros e metros. 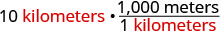
Simplifique. 
Multiplique. 10.000 metros Nick correu 10.000 metros.
Sandy completou sua primeira corrida de 5K! Quantos metros ela correu?
- Resposta
-
5.000 metros
Herman comprou um tapete de 2,5 metros de comprimento. Quantos centímetros tem o comprimento?
- Resposta
-
250 centímetros
O bebê recém-nascido de Eleanor pesava 3.200 gramas. Quantos quilos o bebê pesava?
- Resposta
-
Vamos converter gramas em quilogramas.

Multiplique a medida a ser convertida por 1. 
Escreva 1 como uma função que relaciona quilogramas e gramas. 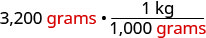
Simplifique. 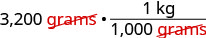
Multiplique. \(\frac{3,200 \text{ kilograms}}{1,000}\) Divida. 3,2 kg
O bebê pesava 3,2 kg.
O bebê recém-nascido de Kari pesava 2.800 gramas. Quantos quilos o bebê pesava?
- Resposta
-
2,8 quilogramas
Anderson recebeu um pacote marcado com 4.500 gramas. Quantos quilos pesava esse pacote?
- Resposta
-
4,5 quilogramas
Ao se familiarizar com o sistema métrico, você pode ver um padrão. Como o sistema é baseado em múltiplos de dez, os cálculos envolvem a multiplicação por múltiplos de dez. Aprendemos como simplificar esses cálculos apenas movendo o decimal.
Para multiplicar por 10, 100 ou 1.000, movemos o decimal para uma, duas ou três casas à direita, respectivamente. Para multiplicar por 0,1, 0,01 ou 0,001, movemos o decimal para a esquerda uma, duas ou três casas, respectivamente.
Podemos aplicar esse padrão quando fazemos conversões de medição no sistema métrico. No Exercício\(\PageIndex{25}\), trocamos 3.200 gramas para quilogramas multiplicando por\(\frac{1}{1000}\) (ou 0,001). Isso é o mesmo que mover as três casas decimais para a esquerda.
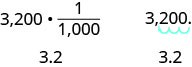
Converta
- 350 L em quilolitros
- 4,1 L a mililitros.
- Resposta
-
1. Vamos converter litros em quilolitros. Na Tabela\(\PageIndex{2}\), vemos que 1 quilolitro=1.000 litros.1 quilolitro=1.000 litros.
350 L Multiplique por 1, escrevendo 1 como uma fração relacionando litros a quilolitros. \(350 \text{ L}\frac{\text{1 kL}}{\text{1000L}}\) Simplifique. \(350 \not{\text{ L}}\frac{\text{1 kL}}{1000 \not\text{ L}}\) 
0,35 kL
2. Vamos converter litros em mililitros. Na tabela,\(\PageIndex{2}\) vemos que 1 litro = 1.000 mililitros.1 litro = 1.000 mililitros.
Multiplique por 1, escrevendo 1 como uma fração relacionando litros a mililitros. 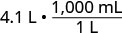
Simplifique. 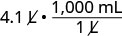
Mova as 3 unidades decimais para a direita. 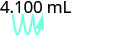

Converter:
- 725 L em quilolitros
- 6.3 L em mililitros
- Resposta
-
- 7.250 quilolitros
- 6.300 mililitros
Converter:
- 350 hL para litros
- 4,1 L a centilitros
- Resposta
-
- 35.000 litros
- 410 centilitros
Use unidades de medida mistas no sistema métrico
A realização de operações aritméticas em medições com unidades mistas de medidas no sistema métrico requer o mesmo cuidado que usamos no sistema dos EUA. Mas pode ser mais fácil por causa da relação das unidades com as potências de 10. Certifique-se de adicionar ou subtrair unidades semelhantes.
Ryland tem 1,6 metros de altura. Seu irmão mais novo tem 85 centímetros de altura. Quanto mais alto é Ryland do que seu irmão mais novo?
- Resposta
-
Podemos converter as duas medidas em centímetros ou metros. Como metros é a unidade maior, subtrairemos os comprimentos em metros. Convertemos 85 centímetros em metros movendo as 2 casas decimais para a esquerda.
\[\begin{array} { cc } { \text {Write the } 85 \text { centimeters as meters. } } & { 1.60 \mathrm { m } } \\ {} &{ \dfrac { - 0.85 \mathrm { m } } { 0.75 \mathrm { m } } } \end{array}\]
Ryland é 0,75 m0,75 m mais alto que seu irmão.
Mariella tem 1,58 metros de altura. A filha dela tem 75 centímetros de altura. Quanto mais alta é Mariella do que sua filha? Escreva a resposta em centímetros.
- Resposta
-
83 centímetros
A cerca ao redor do quintal de Hank tem 2 metros de altura. Hank tem 96 centímetros de altura. Quanto mais curto do que a cerca é Hank? Escreva a resposta em metros.
- Resposta
-
1,04 metros
A receita de sopa de lentilha de Dena exige 150 mililitros de azeite. Dena quer triplicar a receita. Quantos litros de azeite ela precisará?
- Resposta
-
Encontraremos a quantidade de azeite em mililitros e depois converteremos em litros.
\(\begin{array} { ll } {} & { \text { Triple } 150 \text{ mL}} \\ { \text { Translate to algebra. } } &{3\cdot 150 \text{ mL}} \\ { \text { Multiply. } } &{450\text{ mL}}\\ { \text { Convert to liters. } } &{450\cdot \frac{0.001\text{ L}}{1 \text{ ml}}} \\ { \text { Simplify. } } &{0.45 \text{ L}}\\ {} &{ \text { Dena needs 0.45 liters of olive oil. } } \end{array}\)
Uma receita do molho Alfredo exige 250 mililitros de leite. Renata está fazendo macarrão com molho Alfredo para uma grande festa e precisa multiplicar as quantidades da receita por 8. Quantos litros de leite ela precisará?
- Resposta
-
2 litros
Para fazer uma panela de baklava, Dorothea precisa de 400 gramas de massa filo. Se Dorothea planeja fazer 6 panelas de baklava, de quantos quilos de massa filo ela precisará?
- Resposta
-
2,4 quilogramas
Conversão entre os EUA e os sistemas métricos de medição
Muitas medições nos Estados Unidos são feitas em unidades métricas. Nosso refrigerante pode vir em frascos de 2 litros, nosso cálcio pode vir em cápsulas de 500 mg e podemos correr uma corrida de 5K. Para trabalhar facilmente em ambos os sistemas, precisamos ser capazes de converter entre os dois sistemas.
A tabela\(\PageIndex{3}\) mostra algumas das conversões mais comuns.
| Fatores de conversão entre sistemas americanos e métricos | ||
|---|---|---|
| Comprimento | Missa | Capacidade |
| \(\begin{array} { l l l } {1 \text{ in.}} & {=} &{2.54 \text{ cm}} \\ {1\text{ ft.}} &{=} &{0.305 \text{ m}} \\ {1 \text{ yd.}} & {=} &{0.914 \text{ m}} \\ {1\text{ mi.}} &{=} &{1.61 \text{ km}} \\ {1 \text{ m}} & {=} &{3.28 \text{ ft}} \end{array}\) | \(\begin{array} { l l l } {1 \text{ lb.}} & {=} &{0.45 \text{ kg}} \\ {1\text{ oz.}} &{=} &{28 \text{ g}} \\ {1 \text{ kg}} & {=} &{2.2 \text{ lb}} \end{array}\) | \(\begin{array} { l l l } {1 \text{ qt.}} & {=} &{0.95 \text{ L}} \\ {1\text{ fl. oz.}} &{=} &{30 \text{ ml}} \\ {1 \text{ L}} & {=} &{1.06 \text{ lb}} \end{array}\) |
A figura\(\PageIndex{3}\) mostra como polegadas e centímetros estão relacionados em uma régua.

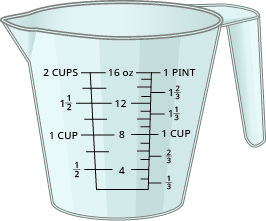
A figura\(\PageIndex{4}\) mostra as marcas de onça e mililitro em um copo medidor.
A figura\(\PageIndex{5}\) mostra como libras e quilos são marcados em uma balança de banheiro.

Fazemos conversões entre os sistemas da mesma forma que fazemos dentro dos sistemas, multiplicando por fatores de conversão unitários.
A garrafa de água de Lee contém 500 mL de água. Quantas onças estão na garrafa? Arredonde para o décimo mais próximo de uma onça.
- Resposta
-
\(\begin{array} { l l } {} & {500 \text{ mL}} \\ {\text{Multiplying by a unit conversion factor relating}} &{500\text{ milliliters}\cdot\frac{1\text{ ounce}}{30\text{ milliliters}}} \\ {\text{mL and ounces}} &{} \\ {\text{Simplify.}} &{\frac{50\text{ ounce}}{30}} \\ {\text{Divide.}} &{16.7\text{ ounces}} \\ {} &{\text{The water bottle has 16.7 ounces}} \end{array}\)
Quantos litros de refrigerante existem em uma garrafa de 2 litros?
- Resposta
-
2,12 quartos
Quantos litros existem em 4 litros de leite?
- Resposta
-
3,8 litros
Soleil estava em uma viagem de carro e viu uma placa que dizia que a próxima parada de descanso seria em 100 quilômetros. Quantos quilômetros até a próxima parada de descanso?
- Resposta
-
\(\begin{array} { l l } {} & {100 \text{ kilometers}} \\ {\text{Multiplying by a unit conversion factor relating}} &{100\text{ kilometers}\cdot\frac{1\text{ mile}}{1.61\text{ kilometers}}} \\ {\text{km and mi.}} &{} \\ {\text{Simplify.}} &{\frac{100\text{ miles}}{1.61}} \\ {\text{Divide.}} &{62\text{ miles}} \\ {} &{\text{Soleil will travel 62 miles.}} \end{array}\)
A altura do Monte Kilimanjaro é de 5.895 metros. Converta a altura em pés.
- Resposta
-
19.335,6 pés
A distância de voo de Nova York a Londres é de 5.586 quilômetros. Converta a distância em milhas.
- Resposta
-
3.469.57 milhas
Conversão entre temperaturas em Fahrenheit e Celsius
Você já esteve em um país estrangeiro e ouviu a previsão do tempo? Se a previsão for de 22°C, o que isso significa?
Os sistemas americano e métrico usam escalas diferentes para medir a temperatura. O sistema dos EUA usa graus Fahrenheit, escritos em °F. O sistema métrico usa graus Celsius, escrito em °C. A figura\(\PageIndex{6}\) mostra a relação entre os dois sistemas.
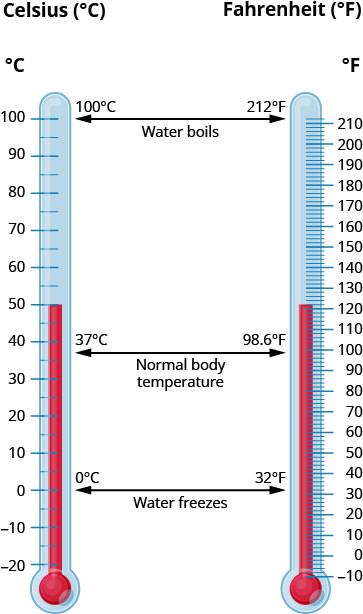
Para converter da temperatura Fahrenheit, F, para temperatura Celsius, C, use a fórmula
\[C = \frac { 5 } { 9 } ( F - 32 )\]
Para converter da temperatura Celsius, C, para a temperatura Fahrenheit, F, use a fórmula
\[F = \frac { 9 } { 5 } C + 32\]
Converta 50° Fahrenheit em graus Celsius.
- Resposta
-
Substituiremos 50° F na fórmula para encontrar C.
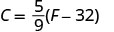

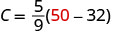
Simplifique entre parênteses. 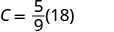
Multiplique. 
Então, descobrimos que 50° F é equivalente a 10° C.
Converta a temperatura em Fahrenheit em graus Celsius: 59° Fahrenheit.
- Resposta
-
15°C
Converta a temperatura em Fahrenheit em graus Celsius: 41° Fahrenheit.
- Resposta
-
5°C
Ao visitar Paris, Woody viu que a temperatura estava em 20° Celsius. Converta a temperatura em graus Fahrenheit.
- Resposta
-
Vamos substituir 20°C na fórmula para encontrar F.
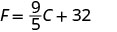

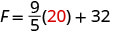
Multiplique. 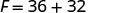
Adicionar. 
Então, descobrimos que 20° C é equivalente a 68° F.
Converta a temperatura Celsius em graus Fahrenheit: a temperatura em Helsinque, Finlândia, foi de 15° Celsius.
- Resposta
-
59°F
Converta a temperatura Celsius em graus Fahrenheit: a temperatura em Sydney, Austrália, foi de 10° Celsius.
- Resposta
-
50°F
Conceitos-chave
- Sistema Métrico de Medição
- Comprimento
1 quilômetro (km) = 1.000 m
1 hectômetro (hm) = 100 m
1 decâmetro (barragem) = 10 m
1 metro (m) = 1 m
1 decímetro (dm) = 0,1 m
1 centímetro (cm) = 0,01 m
1 milímetro (mm) = 0,001 m
1 metro = 100 centímetros
1 metro = 1.000 milímetros
- Missa
1 quilograma (kg) = 1.000 g
1 hectograma (hg) = 100 g
1 dekagrama (dag) = 10 g
1 grama (g) = 1 g
1 decigrama (dg) = 0,1 g
1 centigrama (cg) = 0,01 g
1 miligrama (mg) = 0,001 g
1 grama = 100 centigramas
1 grama = 1.000 miligramas
- Capacidade
1 quilolitro (kL) = 1.000 L
1 hectolitro (hL) = 100 L
1 decalitro (DaL) = 10 L
1 litro (L) = 1 L
1 decilitro (dL) = 0,1 L
1 centilitro (cL) = 0,01 L
1 mililitro (mL) = 0,001 L
1 litro = 100 centilitros
1 litro = 1.000 mililitros
- Conversão de temperatura
- Para converter da temperatura Fahrenheit, F, para temperatura Celsius, C, use a fórmula\(C=\frac{5}{9}(F−32)\)
- Para converter da temperatura Celsius, C, para a temperatura Fahrenheit, F, use a fórmula\(F=\frac{9}{5}C+32\)


