1.10: Propriedades dos números reais
- Page ID
- 184461
Ao final desta seção, você poderá:
- Use as propriedades comutativas e associativas
- Use a identidade e as propriedades inversas de adição e multiplicação
- Use as propriedades de zero
- Simplifique as expressões usando a propriedade distributiva
Uma introdução mais completa aos tópicos abordados nesta seção pode ser encontrada no capítulo Pré-álgebra, As propriedades dos números reais.
Use as propriedades comutativas e associativas
Pense em adicionar dois números, digamos, 5 e 3. A ordem em que os adicionamos não afeta o resultado, não é?
\[\begin{array} { cc } { 5 + 3 } & { 3 + 5 } \\ { 8 } & { 8 } \\ { 5 + 3 = } & { 3 + 5 } \end{array}\]
Os resultados são os mesmos.
Como podemos ver, a ordem em que adicionamos não importa!
Que tal multiplicar 5 por 3?
\[\begin{array} { c c } { 5 \cdot 3 } & { 3 \cdot 5 } \\ { 15 } & { 15 } \\ { 5 \cdot 3=} &{3 \cdot 5 } \end{array}\]
Novamente, os resultados são os mesmos!
A ordem em que multiplicamos não importa!
Esses exemplos ilustram a propriedade comutativa. Ao adicionar ou multiplicar, alterar a ordem dá o mesmo resultado.
\[\begin{array} { l l } { \textbf { of Addition } } & { \text { If } a , b \text { are real numbers, then } \quad a + b = b + a } \\ { \textbf { of Multiplication } } & { \text { If } a , b \text { are real numbers, then } \quad a \cdot b = b \cdot a } \end{array}\]
Ao adicionar ou multiplicar, alterar a ordem dá o mesmo resultado.
A propriedade comutativa tem a ver com a ordem. Se você alterar a ordem dos números ao adicionar ou multiplicar, o resultado será o mesmo.
E quanto à subtração? A ordem importa quando subtraímos números? 7−3 dá o mesmo resultado que 3−7?
\[\begin{array} { c c } { 7 - 3 } & { 3 - 7 } \\ { 4 } & { - 4 } \end{array}\]
\[\begin{aligned} 4 & \neq - 4 \\ 7 - 3 & \neq 3 - 7 \end{aligned}\]
Os resultados não são os mesmos.
Como a alteração da ordem da subtração não deu o mesmo resultado, sabemos que a subtração não é comutativa.
Vamos ver o que acontece quando dividimos dois números. A divisão é comutativa?
\[\begin{array} { cc} { 12 \div 4 } & { 4 \div 12 } \\ { \frac { 12 } { 4 } } & { \frac { 4 } { 12 } } \\ { 3 } & { \frac { 1 } { 3 } } \end{array}\]
\[\begin{aligned} 3 \neq & \frac { 1 } { 3 } \\ 12 \div 4 & \neq 4 \div 12 \end{aligned}\]
Os resultados não são os mesmos.
Como a alteração da ordem da divisão não deu o mesmo resultado, a divisão não é comutativa. As propriedades comutativas só se aplicam à adição e multiplicação!
- A adição e a multiplicação são comutativas.
- Subtração e divisão não são comutativas.
Se você fosse solicitado a simplificar essa expressão, como você faria isso e qual seria sua resposta?
\[7 + 8 + 2\]
Algumas pessoas pensariam que\(7+8\) é 15 e depois\(15+2\) 17. Outros podem começar com\(8+2\) marcas 10 e depois\(7+10\) 17.
De qualquer forma, dá o mesmo resultado. Lembre-se de que usamos parênteses como símbolos de agrupamento para indicar qual operação deve ser feita primeiro.
\[\begin{array} { ll } { \text{ Add } 7 + 8 . } & { ( 7 + 8 ) + 2 } \\ { \text { Add. } } & { 15 + 2 } \\ { \text { Add. } } & { 17 } \\ \\ { } & { 7 + ( 8 + 2 ) } \\ { \text { Add } 8 + 2 . } & { 7 + 10 } \\ { \text { Add. } } & { 77 } \\\\ { ( 7 + 8 ) + 2 = 7 + ( 8 + 2 ) } \end{array}\]
Ao adicionar três números, alterar o agrupamento dos números dá o mesmo resultado.
Isso também vale para a multiplicação.
\[\begin{array} { ll } { } & { (5\cdot \frac{1}{3})\cdot 3 } \\ { \text { Multiply. } 5\cdot \frac{1}{3} } & { \frac{5}{3}\cdot 3 } \\ { \text { Multiply. } } & { 5 } \\ \\ { } & { 5\cdot (\frac{1}{3}\cdot 3) } \\ { \text { Multiply. } \frac{1}{3}\cdot 3 } & { 5\cdot 1 } \\ { \text { Multiply. } } & { 5 } \\ \\ { (5\cdot \frac{1}{3})\cdot 3 = 5\cdot (\frac{1}{3}\cdot 3) } \end{array}\]
Ao multiplicar três números, alterar o agrupamento dos números dá o mesmo resultado.
Você provavelmente sabe disso, mas a terminologia pode ser nova para você. Esses exemplos ilustram a propriedade associativa.
\[\begin{array} { l l } { \textbf { of Addition } } & { \text { If } a , b , c \text { are real numbers, then } ( a + b ) + c = a + ( b + c ) } \\ { \textbf { of Multiplication } } & { \text { If } a , b , c \text { are real numbers, then } ( a \cdot b ) \cdot c = a \cdot ( b \cdot c ) } \end{array}\]
Ao adicionar ou multiplicar, alterar o agrupamento dá o mesmo resultado.
Vamos pensar novamente sobre a multiplicação\(5\cdot \frac{1}{3}\cdot 3\). Obtivemos o mesmo resultado nos dois sentidos, mas qual foi o mais fácil? Multiplicar\(\frac{1}{3}\) e 3 primeiro, conforme mostrado acima no lado direito, elimina a fração na primeira etapa. Usar a propriedade associativa pode facilitar a matemática!
A propriedade associativa tem a ver com agrupamento. Se mudarmos a forma como os números são agrupados, o resultado será o mesmo. Observe que são os mesmos três números na mesma ordem — a única diferença é o agrupamento.
Vimos que a subtração e a divisão não eram comutativas. Eles também não são associativos.
Ao simplificar uma expressão, é sempre uma boa ideia planejar quais serão as etapas. Para combinar termos semelhantes no próximo exemplo, usaremos a propriedade comutativa da adição para escrever os termos semelhantes juntos.
Simplifique:\(18p+6q+15p+5q\).
- Responda
-
\[\begin{array} { l l} {} &{18p+6q+15p+5q}\\ \\{ \text { Use the commutative property of addition } } &{} \\ { \text {to re-order so that like terms are together.} } &{18p+15p+ 6q+5q} \\ \\ {\text{Add like terms.}} &{33p + 11q} \end{array}\]
Simplifique:\(23r+14s+9r+15s\).
- Responda
-
\(32r+29s\)
Simplifique:\(37m+21n+4m−15n\).
- Responda
-
\(41m+6n\)
Quando precisamos simplificar a expressão algébrica s, muitas vezes podemos facilitar o trabalho aplicando primeiro a propriedade comutativa ou associativa, em vez de seguir automaticamente a ordem das operações. Ao adicionar ou subtrair frações, combine-as primeiro com um denominador comum.
Simplifique:\((\frac{5}{13} + \frac{3}{4}) + \frac{1}{4}\)
- Responda
-
\[\begin{array} { l l } {} &{(\frac{5}{13} + \frac{3}{4}) + \frac{1}{4}} \\{ \text { Notice that the last } 2 \text { terms have a } } \\ { \text { common denominator, so change the } } &{\frac { 5 } { 13 } + \left( \frac { 3 } { 4 } + \frac { 1 } { 4 } \right)}\\ { \text { grouping. } } &{}\\ \\ {\text{Add in parentheses first.}} &{\frac{5}{13} + (\frac{4}{4})} \\ \\ {\text{Simplify the fraction.}} &{\frac{5}{13} + 1} \\ \\ {\text{Add.}} &{1\frac{5}{13}} \\ \\ {\text{Convert to an improper fraction.}} &{\frac{18}{13}} \end{array}\]
Simplifique:\((\frac{7}{15} + \frac{5}{8}) + \frac{3}{8}\)
- Responda
-
\(1\frac{7}{15}\)
Simplifique:\((\frac{2}{9} + \frac{7}{12}) + \frac{5}{12}\)
- Responda
-
\(1\frac{2}{9}\)
Use a propriedade associativa para simplificar\(6(3x)\).
- Responda
-
Use a propriedade associativa da multiplicação,\((a\cdot b)\cdot c=a\cdot (b\cdot c)\), para alterar o agrupamento.
\[\begin{array} { ll } {} &{ 6 ( 3 x ) } \\ { \text { Change the grouping. } } &{(6\cdot 3)x} \\ { \text { Multiply in the parentheses. } } &{18} \end{array}\]
Observe que podemos multiplicar\(6\cdot 3\), mas não podemos multiplicar\(3x\) sem ter um valor para\(x\).
Use a propriedade associativa para simplificar\(8(4x)\).
- Responda
-
\(32x\)
Use a propriedade associativa para simplificar\(-9(7y)\).
- Responda
-
\(-63y\)
Use a identidade e as propriedades inversas de adição e multiplicação
O que acontece quando adicionamos 0 a qualquer número? Adicionar 0 não altera o valor. Por esse motivo, chamamos 0 de identidade aditiva.
Por exemplo,
\[\begin{array} { c c c } { 13 + 0 } & { - 14 + 0 } & { 0 + ( - 8 ) } \\ { 13 } & { - 14 } & { - 8 } \end{array}\]
Esses exemplos ilustram a propriedade de adição de identidade que afirma que, para qualquer número real\(a\),\(a+0=a\)\(0+a=a\) e.
O que acontece quando multiplicamos qualquer número por um? Multiplicar por 1 não altera o valor. Então, chamamos 1 de identidade multiplicativa.
Por exemplo,\[\begin{array} { r r r } { 43 \cdot 1 } & { - 27 \cdot 1 } & { 1 \cdot \frac { 3 } { 5 } } \\ { 43 } & { - 27 } & { \frac { 3 } { 5 } } \end{array}\]
Esses exemplos ilustram a propriedade de multiplicação de identidade que afirma que, para qualquer número real\(a\),\(a\cdot 1=a\)\(1\cdot a=a\) e.
Resumimos as propriedades de identidade abaixo.
\[\begin{array} { l l} { \textbf {of addition}\text{ For any real number } a : } &{ a + 0 = a \quad 0 + a = a } \\ { \textbf{0} \text { is the}\textbf{ additive identity } } \\ {\textbf {of multiplication}\text{ For any real number } a : } &{ a \cdot 1 = a \quad 1 \cdot a = a } \\ { \textbf{1}\text{ is the}\textbf{ multiplicative identity } } \end{array}\]

Observe que, em cada caso, o número que faltava era o oposto do número!
Nós chamamos de\(−a\). o inverso aditivo de a. O oposto de um número é seu inverso aditivo. Um número e seu oposto se somam a zero, que é a identidade aditiva. Isso leva à Propriedade Inversa de Adição, que indica para qualquer número real\(a, a+(−a)=0\). Lembre-se de que um número e seu oposto se somam a zero.
Qual número multiplicado por\(\frac{2}{3}\) dá a identidade multiplicativa, 1? Em outras palavras,\(\frac{2}{3}\) vezes o que resulta em 1?

Qual número multiplicado por 2 dá a identidade multiplicativa, 1? Em outras palavras, 2 vezes o que resulta em 1?

Observe que, em cada caso, o número que faltava era o inverso do número!
Chamamos\(\frac{1}{a}\) o inverso multiplicativo de a. O inverso de um número é seu inverso multiplicativo. Um número e seu recíproco se multiplicam por um, que é a identidade multiplicativa. Isso leva à Propriedade Inversa de Multiplicação, que afirma isso para qualquer número real\(a, a\neq 0, a\cdot \frac{1}{a}=1\).
Declararemos formalmente as propriedades inversas aqui:
\[\begin{array} { l l l } { \textbf { of addition } } &{ \text { For any real number } a,} &{a + (-a) = 0}\\{} &{-a \text{. is the}\textbf{ additive inverse} \text{ of }a} &{}\\ {} &{ \text { A number and its opposite add to zero. } }&{}\\ \\{ \textbf { of multiplication } } &{ \text { For any real number } a, a\neq 0} &{a\cdot \frac{1}{a} = 1}\\{} &{\frac{1}{a} \text{. is the}\textbf{ multiplicative inverse} \text{ of }a} &{}\\ {} &{ \text { A number and its reciprocal multiply to zero. } }&{} \end{array}\]
Encontre o inverso aditivo de
- \(\frac{5}{8}\)
- \(0.6\)
- \(-8\)
- \(-\frac{4}{3}\)
- Responda
-
Para encontrar o inverso do aditivo, encontramos o oposto.
- O inverso aditivo de\(\frac{5}{8}\) é o oposto de\(\frac{5}{8}\). O inverso aditivo de\(\frac{5}{8}\) é\(-\frac{5}{8}\)
- O inverso aditivo de\(0.6\) é o oposto de\(0.6\). O inverso aditivo de\(0.6\) é\(-0.6\).
- O inverso aditivo de\(-8\) é o oposto de\(-8\). Escrevemos o oposto de\(-8\) as\(-(-8)\) e depois simplificamos para\(8\). Portanto, o inverso aditivo de\(-8\) é\(8\).
- O inverso aditivo de\(-\frac{4}{3}\) é o oposto de\(-\frac{4}{3}\). Escrevemos isso como\(-(-\frac{4}{3})\) e depois simplificamos para\(\frac{4}{3}\). Assim, o inverso aditivo de\(-\frac{4}{3}\) é\(\frac{4}{3}\).
Encontre o inverso aditivo de
- \(\frac{7}{9}\)
- \(1.2\)
- \(-14\)
- \(-\frac{9}{4}\)
- Resposta
-
- \(-\frac{7}{9}\)
- \(-1.2\)
- \(14\)
- \(\frac{9}{4}\)
Encontre o inverso aditivo de
- \(\frac{7}{13}\)
- \(8.4\)
- \(-46\)
- \(-\frac{5}{2}\)
- Resposta
-
- \(-\frac{7}{13}\)
- \(-8.4\)
- \(46\)
- \(\frac{5}{2}\)
Encontre o inverso multiplicativo de
- \(9\)
- \(-\frac{1}{9}\)
- \(0.9\)
- Resposta
-
Para encontrar o inverso multiplicativo, encontramos o recíproco.
- O inverso multiplicativo de\(9\) é o inverso de\(9\), que é\(\frac{1}{9}\). Portanto, o inverso multiplicativo de\(9\) é\(\frac{1}{9}\).
- O inverso multiplicativo de\(-\frac{1}{9}\) é o inverso de\(-\frac{1}{9}\), que é\(−9\). Assim, o inverso multiplicativo de\(-\frac{1}{9}\) é\(-9\).
- Para encontrar o inverso multiplicativo de\(0.9\), primeiro\(0.9\) convertemos em uma fração,\(\frac{9}{10}\). Em seguida, encontramos o recíproco da fração. O recíproco de\(\frac{9}{10}\) é\(\frac{10}{9}\). Então, o inverso multiplicativo de\(0.9\) é\(\frac{10}{9}\).
Encontre o inverso multiplicativo de
- \(4\)
- \(-\frac{1}{7}\)
- \(0.3\)
- Resposta
-
- \(\frac{1}{4}\)
- \(-7\)
- \(\frac{10}{3}\)
Encontre o inverso multiplicativo de
- \(18\)
- \(-\frac{4}{5}\)
- \(0.6\)
- Resposta
-
- \(\frac{1}{18}\)
- \(-\frac{5}{4}\)
- \(\frac{5}{3}\)
Use as propriedades de Zero
A propriedade de adição de identidade diz que quando adicionamos 0 a qualquer número, o resultado é o mesmo número. O que acontece quando multiplicamos um número por 0? Multiplicar por 0 torna o produto igual a zero.
Para qualquer número real a.
\[a \cdot 0 = 0 \quad 0 \cdot a = 0\]
O produto de qualquer número real e 0 é 0.
E quanto à divisão envolvendo zero? O que é\(0\div 3\)? Pense em um exemplo real: se não houver biscoitos no pote de biscoitos e 3 pessoas quiserem compartilhá-los, quantos biscoitos cada pessoa recebe? Não há cookies para compartilhar, então cada pessoa recebe 0 cookies. Então,
\[0\div 3 = 0\]
Podemos verificar a divisão com o fato de multiplicação relacionado.
\[12 \div 6 = 2 \text { because } 2 \cdot 6 = 12\]
Então, sabemos\(0\div 3=0\) porque\(0\cdot 3=0\).
Para qualquer número real a, exceto\(0, \frac{0}{a}=0\)\(0\div a=0\) e.
Zero dividido por qualquer número real, exceto zero é zero.
Agora pense em dividir por zero. Qual é o resultado da divisão de 4 por 0? Pense no fato relacionado à multiplicação:\(4\div 0=?\) meios\(?\cdot 0=4\). Existe um número que multiplicado por 0 dá 4? Como qualquer número real multiplicado por 0 dá 0, não há número real que possa ser multiplicado por 0 para obter 4.
Concluímos que não há resposta para\(4\div 0\) e, portanto, dizemos que a divisão por 0 é indefinida.
Para qualquer número real a, exceto\(0, \frac{a}{0}\) e\(a\div 0\) são indefinidos.
A divisão por zero é indefinida.
Resumimos as propriedades de zero abaixo.
Multiplicação por Zero: Para qualquer número real a,
\[a \cdot 0 = 0 \quad 0 \cdot a = 0 \quad \text { The product of any number and } 0 \text { is } 0\]
Divisão de Zero, Divisão por Zero: Para qualquer número real\(a, a\neq 0\)
\[\begin{array} { l l } { \frac { 0 } { a } = 0 } & { \text { Zero divided by any real number, except itself is zero. } } \\ { \frac { a } { 0 } \text { is undefined } } & { \text { Division by zero is undefined. } } \end{array}\]
Simplifique:
- \(-8\cdot 0\)
- \(\frac{0}{-2}\)
- \(\frac{-32}{0}\)
- Resposta
-
- \[\begin{array} { cc } { } &{-8\cdot 0}\\{\text{The product of any real number and 0 is 0}} &{0}\end{array}\]
- \[\begin{array} { ll } { } &{\frac{0}{-2}}\\{\text{Zero divided by any real number, except}} &{} \\ {\text{itself, is 0}} &{0}\end{array}\]
- \[\begin{array} { ll } { } &{\frac{-32}{0}}\\ {\text{Division by 0 is undefined.}} &{\text{undefined}} \end{array}\]
Simplifique:
- \(-14\cdot 0\)
- \(\frac{0}{-6}\)
- \(\frac{-2}{0}\)
- Resposta
-
- \(0\)
- \(0\)
- indefinida
Simplifique:
- \(0(-17)\)
- \(\frac{0}{-10}\)
- \(\frac{-5}{0}\)
- Resposta
-
- \(0\)
- \(0\)
- indefinida
Agora praticaremos o uso das propriedades de identidades, inversas e zero para simplificar expressões.
Simplifique:
- \(\frac{0}{n + 5}\), onde\(n\neq −5\)
- \(\frac{10 - 3p}{0}\)onde\(10 - 3p \neq 0\)
- Resposta
-
- \[\begin{array} { ll } { } &{\frac{0}{n + 5}}\\ {\text { Zero divided by any real number except }} &{0} \\ { \text { itself is } 0.} &{} \end{array}\]
- \[\begin{array} { ll } { } &{\frac{10 - 3p}{0}}\\ {\text { Division by 0 is undefined }} &{\text{undefined}} \end{array}\]
Simplifique:\(−84n+(−73n)+84n\).
- Resposta
-
\[\begin{array} { l l } { } &{−84n+(−73n)+84n} \\ { \text { Notice that the first and third terms are } } &{}\\ { \text { opposites; use the commutative property of } } &{- 84 n + 84 n + ( - 73 n ) } \\ { \text { addition to re-order the terms. } } &{} \\ \\ { \text { Add left to right. } } &{0 + (-73)}\\ \\{ \text { Add. } } &{-73n} \end{array}\]
Simplifique:\(−27a+(−48a)+27a\).
- Resposta
-
\(−48a\)
Simplifique:\(39x+(−92x)+(−39x)\).
- Resposta
-
\(−92x\)
Agora veremos como reconhecer os recíprocos é útil. Antes de multiplicar da esquerda para a direita, procure por recíprocos — o produto deles é 1.
Simplifique:\(\frac{7}{15}\cdot\frac{8}{23}\cdot\frac{15}{7}\)
- Resposta
-
\[\begin{array} { l l } { } &{\frac{7}{15}\cdot\frac{8}{23}\cdot\frac{15}{7}} \\ { \text { Notice that the first and third terms are } } &{}\\ { \text { reciprocals, so use the commutative } } &{\frac{7}{15}\cdot\frac{15}{7}\cdot\frac{8}{23}} \\ { \text { property of multiplication to re-order the } } &{} \\ { \text { factors. } } &{}\\ \\{ \text { Multiply left to right. } } &{1\cdot\frac{8}{23}} \\\\{\text{Multiply.}} &{\frac{8}{23}}\end{array}\]
Simplifique:\(\frac{9}{16}\cdot\frac{5}{49}\cdot\frac{16}{9}\)
- Resposta
-
\(\frac{5}{49}\)
Simplifique:\(\frac{6}{17}\cdot\frac{11}{25}\cdot\frac{17}{6}\)
- Resposta
-
\(\frac{11}{25}\)
Simplifique:
- \(\frac{0}{m + 7}\), onde\(m \neq -7\)
- \(\frac{18 - 6c}{0}\), onde\(18 - 6c \neq 0\)
- Resposta
-
- 0
- indefinida
Simplifique:
- \(\frac{0}{d - 4}\), onde\(d \neq 4\)
- \(\frac{15 - 4q}{0}\), onde\(15 - 4q \neq 0\)
- Resposta
-
- 0
- indefinida
Simplifique:\(\frac{3}{4}\cdot\frac{4}{3}(6x + 12)\)
- Resposta
-
\[\begin{array} { l l } { } &{\frac{3}{4}\cdot\frac{4}{3}(6x + 12)} \\ { \text { There is nothing to do in the parentheses, } } &{}\\ { \text { so multiply the two fractions first—notice, } } &{1(6x + 12)} \\ { \text { they are reciprocals. } } &{} \\ \\{ \text { Simplify by recognizing the multiplicative } } &{} \\{\text{ identity.}} &{6x + 12} \end{array}\]
Simplifique:\(\frac{2}{5}\cdot\frac{5}{2}(20y + 50)\)
- Resposta
-
\(20y + 50\)
Simplifique:\(\frac{3}{8}\cdot\frac{8}{3}(12z + 16)\)
- Resposta
-
\(12z + 16\)
Simplifique as expressões usando a propriedade distributiva
Suponha que três amigos estejam indo ao cinema. Cada um deles precisa de $9,25, ou seja, 9 dólares e 1 quarto, para pagar seus ingressos. De quanto dinheiro eles precisam juntos?
Você pode pensar nos dólares separadamente dos trimestres. Eles precisam de 3 vezes $9, então $27, e 3 vezes 1 quarto, então 75 centavos. No total, eles precisam de $27,75. Se você pensar em fazer as contas dessa maneira, você está usando a propriedade distributiva.
\[\begin{array} { rr } {\text { If } a , b , c \text { are real numbers, then }} &{a ( b + c ) = a b + a c} \\ \\{ \text { Also,} } &{( b + c ) a = b a + c a} \\ {} &{a ( b - c ) = a b - a c } &{} \\{} &{( b - c ) a = b a - c a } \end{array}\]
Voltando aos nossos amigos do cinema, pudemos encontrar a quantia total de dinheiro que eles precisam assim:
\[\begin{array} { c } { 3 ( 9.25 ) } \\ { 3 ( 9 + 0.25 ) } \\ { 3 ( 9 ) + 3 ( 0.25 ) } \\ { 27 + 0.75 } \\ \\ { 27.75 } \end{array}\]
Em álgebra, usamos a propriedade distributiva para remover parênteses à medida que simplificamos as expressões.
Por exemplo, se formos solicitados a simplificar a expressão\(3(x+4)\), a ordem das operações diz que devemos trabalhar primeiro entre parênteses. Mas não podemos adicionar x e 4, pois eles não são como termos. Então, usamos a propriedade distributiva, conforme mostrado no Exercício\(\PageIndex{31}\).
Simplifique:\(3(x+4)\).
- Resposta
-
\[\begin{array} { l l } { } & { 3 ( x + 4 ) } \\ { \text { Distribute. } } & { 3 \cdot x + 3 \cdot 4 } \\ { \text { Multiply. } } & { 3 x + 12 } \end{array}\]
Simplifique:\(4(x+2)\).
- Resposta
-
\(4x + 8\)
Simplifique:\(6(x+7)\).
- Resposta
-
\(6x + 42\)
Alguns estudantes acham útil desenhar setas para lembrá-los de como usar a propriedade distributiva. Então, a primeira etapa do Exercício\(\PageIndex{31}\) ficaria assim:
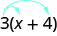
Simplifique:\(8(\frac{3}{8}x+\frac{1}{4})\).
- Resposta
-
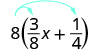
Distribuir. 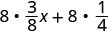
Multiplique. 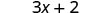
Simplifique:\(6(\frac{5}{6}y+\frac{1}{2})\).
- Resposta
-
\(5y + 3\)
Simplifique:\(12(\frac{1}{3}n+\frac{3}{4})\).
- Resposta
-
\(4n + 9\)
Usar a propriedade distributiva, conforme mostrado no Exercício,\(\PageIndex{37}\) será muito útil quando resolvermos aplicações de dinheiro em capítulos posteriores.
Simplifique:\(100(0.3+0.25q)\).
- Resposta
-
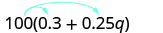
Distribuir. 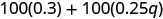
Multiplique. 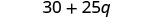
Simplifique:\(100(0.7+0.15p)\).
- Resposta
-
\(70 + 15p\)
Simplifique:\(100(0.04+0.35d)\).
- Resposta
-
\(4 + 35d\)
Quando distribuímos um número negativo, precisamos ter muito cuidado para corrigir os sinais!
Simplifique:\(−2(4y+1)\).
- Resposta
-
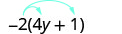
Distribuir. 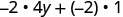
Multiplique. 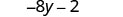
Simplifique:\(−3(6m+5)\).
- Resposta
-
\(−18m-15)\)
Simplifique:\(−6(8n+11)\).
- Resposta
-
\(−48n- 66)\)
Simplifique:\(−11(4-3a)\).
- Resposta
-
Distribuir. 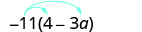
Multiplique. 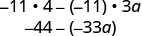
Simplifique. 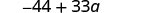
Observe que você também pode escrever o resultado como\(33a−44\). Você sabe por quê?
Simplifique:\(−5(2-3a)\).
- Resposta
-
\(10+ 15a\)
Simplifique:\(−7(8-15y)\).
- Resposta
-
\(-56 + 105y\)
O exercício\(\PageIndex{46}\) mostrará como usar a propriedade distributiva para encontrar o oposto de uma expressão.
Simplifique:\(−(y+5)\).
- Resposta
-
\[\begin{array} { ll } {} &{-(y + 5)} \\ \\{ \text {Multiplying by -1 results in the opposite.} } &{-1( y + 5 )} \\ \\ {\text{Distribute.}} &{-1\cdot y + (-1)\cdot 5}\\ \\{\text{Simplify.}} &{-y + (-5)} \\ \\ {} &{-y - 5} \end{array}\]
Simplifique:\(−(z-11)\).
- Resposta
-
\(-z + 11\)
Simplifique:\(−(x -4)\).
- Resposta
-
\(-x + 4\)
Haverá momentos em que precisaremos usar a propriedade distributiva como parte da ordem das operações. Comece examinando os parênteses. Se a expressão dentro dos parênteses não puder ser simplificada, a próxima etapa seria multiplicar usando a propriedade distributiva, que remove os parênteses. Os próximos dois exemplos ilustrarão isso.
Simplifique:\(8−2(x + 3)\).
Certifique-se de seguir a ordem das operações. A multiplicação vem antes da subtração, então vamos distribuir o 2 primeiro e depois subtrair.
- Resposta
-
\[\begin{array} { ll } {} &{8−2(x + 3)} \\ \\{ \text {Distribute.} } &{8−2\cdot x -2\cdot 3} \\ \\ {\text{Multiply.}} &{8 - 2x - 6}\\ \\{\text{Combine like terms.}} &{-2x + 2} \end{array}\]
Simplifique:\(9−3(x + 2)\).
- Resposta
-
\(3 - 3x\)
Simplifique:\(7x−5(x + 4)\).
- Resposta
-
\(2x - 20\)
Simplifique:\(4(x - 8)−(x + 3)\).
- Resposta
-
\[\begin{array} { ll } {} &{4(x - 8)−(x + 3)} \\ \\{ \text {Distribute.} } &{4x - 32 - x - 3} \\ \\{\text{Combine like terms.}} &{3x - 35} \end{array}\]
Simplifique:\(6(x - 9)−(x + 12)\).
- Resposta
-
\(5x - 66\)
Simplifique:\(8(x - 1)-(x + 5)\).
- Resposta
-
\(7x - 13\)
Todas as propriedades dos números reais que usamos neste capítulo estão resumidas na Tabela\(\PageIndex{1}\).
| Propriedade comutativa | |
| de adição Se a, b são números reais, então de multiplicação Se a, b são números reais, então |
\(a+b=b+a\) \(a\cdot b=b\cdot a\) |
| Propriedade associativa | |
| de adição Se a, b, c são números reais, então de multiplicação Se a, b, c são números reais, então |
\((a+b)+c=a+(b+c)\) \((a\cdot b)\cdot c=a\cdot (b\cdot c)\) |
| Propriedade distributiva | |
| Se a, b, c são números reais, então | \(a(b+c)=ab+ac\) |
| Propriedade de identidade | |
|
de adição Para qualquer número real a: de multiplicação Para qualquer número real a: |
\(a+0=a\) \(0+a=a\) \(1·a=a\) |
| Propriedade inversa | |
| de adição Para qualquer número real a, \(−a\) é o inverso aditivo de a da multiplicação Para qualquer número real\(a,a\neq 0\) \(\frac{1}{a}\) é o inverso multiplicativo de a |
\(a+(−a)=0\) \(a\cdot\frac{1}{a}=1\) |
| Propriedades do Zero | |
|
Para qualquer número real a, Para qualquer número real\(a,a\neq 0\) |
\(a\cdot 0=0\) \(0\cdot a=0\) \(\frac{0}{a} = 0\) |
Conceitos-chave
- Propriedade comutativa de
- Adição: Se a, b são números reais, então\(a+b=b+a\).
- Multiplicação: Se a, b são números reais, então\(a\cdot b=b\cdot a\). Ao adicionar ou multiplicar, alterar a ordem dá o mesmo resultado.
- Propriedade associativa de
- Adição: Se a, b, c são números reais, então\((a+b)+c=a+(b+c)\).
- Multiplicação: Se a, b, c são números reais, então\((a\cdot b)\cdot c=a\cdot (b\cdot c)\).
Ao adicionar ou multiplicar, alterar o agrupamento dá o mesmo resultado.
- Propriedade distributiva: Se a, b, c são números reais, então
- \(a(b+c)=ab+ac\)
- \((b+c)a=ba+ca\)
- \(a(b-c)=ab-ac\)
- \((b+c)a=ba-ca\)
- Propriedade de identidade
- de adição: Para qualquer número real a:\(a+0=a\)
0 é a identidade aditiva - da multiplicação: Para qualquer número real a:\(a\cdot 1=a \quad 1·a=a\)
1 1 é a identidade multiplicativa
- de adição: Para qualquer número real a:\(a+0=a\)
- Propriedade inversa
- de adição: Para qualquer número real\(a, a+(−a)=0\). Um número e seu oposto se somam a zero. \(−a\)é o inverso aditivo de a.
- de multiplicação: Para qualquer número real\(a,(a\neq 0)a\cdot\frac{1}{a}=1\). Um número e seu recíproco se multiplicam por um. \(\frac{1}{a}\)é o inverso multiplicativo de a.
- Propriedades do Zero
- Para qualquer número real a,
\(a\cdot 0=0 \quad 0·a=0\) — O produto de qualquer número real e 0 é 0. - \(\frac{0}{a}=0\)for\(a\neq 0\) — Zero dividido por qualquer número real, exceto que zero é zero.
- \(\frac{a}{0}\)é indefinido — A divisão por zero é indefinida.
- Para qualquer número real a,


