Skip to main content
Global

1.9: Os números reais

  1. Last updated
  2. Save as PDF
  • Page ID
    184450

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    objetivos de aprendizagem

    Ao final desta seção, você poderá:

    • Simplifique expressões com raízes quadradas
    • Identifique números inteiros, números racionais, números irracionais e números reais
    • Localize frações na reta numérica
    • Localize números decimais na reta numérica
    Nota

    Uma introdução mais completa aos tópicos abordados nesta seção pode ser encontrada nos capítulos de Pré-álgebra, Decimais e Propriedades de Números Reais.

    Simplifique expressões com raízes quadradas

    Lembre-se de que quando um número\(n\) é multiplicado por si mesmo, nós o escrevemos\(n^{2}\) e lemos “\(n\)ao quadrado”. O resultado é chamado de quadrado de\(n\). Por exemplo,

    \[\begin{array} { l l } { 8 ^ { 2 } } & { \text { read '8 squared' } } \\ { 64 } & { 64 \text { is called the square of } 8 \text { . } } \end{array}\]

    Da mesma forma, 121 é o quadrado de 11, porque\(11^{2}\) é 121.

    QUADRADO DE UM NÚMERO

    Se\(n^{2}=m\), então\(m\) é o quadrado de\(n\).

    Nota

    Fazer a atividade de Matemática Manipulativa “Números Quadrados” ajudará você a desenvolver uma melhor compreensão dos números quadrados perfeitos.

    Complete a tabela a seguir para mostrar os quadrados dos números de contagem de 1 a 15.

    Há uma tabela com duas linhas e 17 colunas. A primeira linha é lida da esquerda para a direita Number, n, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 e 15. A segunda linha é lida da esquerda para a direita Quadrado, n ao quadrado, em branco, em branco, em branco, em branco, em branco, 64, em branco, em branco, 121, em branco, em branco, em branco e em branco.
    Figura\(\PageIndex{1}\)

    Os números na segunda linha são chamados de números quadrados perfeitos. Será útil aprender a reconhecer os números quadrados perfeitos.

    Os quadrados dos números contados são números positivos. E quanto aos quadrados dos números negativos? Sabemos que quando os sinais de dois números são iguais, o produto deles é positivo. Portanto, o quadrado de qualquer número negativo também é positivo.

    \[( - 3 ) ^ { 2 } = 9 \quad ( - 8 ) ^ { 2 } = 64 \quad ( - 11 ) ^ { 2 } = 121 \quad ( - 15 ) ^ { 2 } = 225\]

    Você notou que esses quadrados são iguais aos quadrados dos números positivos?

    Às vezes, precisaremos observar a relação entre números e seus quadrados ao contrário. Porque\(10^{2}=100\), dizemos que 100 é o quadrado de 10. Também dizemos que 10 é uma raiz quadrada de 100. Um número cujo quadrado é mm é chamado de raiz quadrada de\(m\).

    RAIZ QUADRADA DE UM NÚMERO

    Se\(n^{2}=m\), então\(n\) é uma raiz quadrada de\(m\).

    Observe\((−10)^{2}=100\) também, então também\(−10\) é uma raiz quadrada de\(100\). Portanto, ambos\(10\) e\(−10\) são raízes quadradas de\(100\).

    Então, todo número positivo tem duas raízes quadradas — uma positiva e uma negativa. E se quiséssemos apenas a raiz quadrada positiva de um número positivo? O sinal radical,\(\sqrt{m}\), indica a raiz quadrada positiva. A raiz quadrada positiva é chamada de raiz quadrada principal. Quando usamos o sinal radical, isso sempre significa que queremos a raiz quadrada principal.

    Também usamos o sinal radical para a raiz quadrada de zero. Porque\(0^{2}=0, \sqrt{0}=0\). Observe que zero tem apenas uma raiz quadrada.

    NOTAÇÃO DE RAIZ QUADRADA

    \(\sqrt{m}\)é lido “a raiz quadrada de\(m\)”

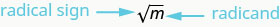
    Uma raiz quadrada é dada, com uma seta para o sinal radical (parece uma marca de verificação com uma linha horizontal que se estende de sua extremidade longa) denotada como sinal radical e uma seta para o número abaixo do sinal radical, que está marcado como radicando.

    Se\(m = n^{2}\), então\(\sqrt{m} = n\), para\(n\geq 0\).

    A raiz quadrada de\(m\)\(\sqrt{m}\),, é o número positivo cujo quadrado é\(m\).

    Como 10 é a raiz quadrada principal de 100, escrevemos\(\sqrt{100}=10\). Talvez você queira preencher a tabela a seguir para ajudá-lo a reconhecer raízes quadradas.

    Há uma tabela com duas linhas e 15 colunas. A primeira linha diz da esquerda para a direita raiz quadrada de 1, raiz quadrada de 4, raiz quadrada de 9, raiz quadrada de 16, raiz quadrada de 25, raiz quadrada de 36, raiz quadrada de 49, raiz quadrada de 64, raiz quadrada de 81, raiz quadrada de 100, raiz quadrada de 121, raiz quadrada de 144, raiz quadrada de 169, raiz quadrada de 196 e raiz quadrada de 225. A segunda linha consiste em todos os espaços em branco, exceto pela décima célula abaixo da raiz quadrada de 100, que diz 10.
    Figura\(\PageIndex{2}\)
    Exercício\(\PageIndex{1}\)

    Simplifique:

    1. \(\sqrt{25}\)
    2. \(\sqrt{121}\)
    Responda
    1. \[\begin{array} {ll} {} &{\sqrt{25}} \\ {\text {Since }5^{2} = 25} &{5} \end{array}\]
    2. \[\begin{array} {ll} {} &{\sqrt{121}} \\ {\text {Since }11^{2} = 121} &{11} \end{array}\]
    Exercício\(\PageIndex{2}\)

    Simplifique:

    1. \(\sqrt{36}\)
    2. \(\sqrt{169}\)
    Responda
    1. 6
    2. 13
    Exercício\(\PageIndex{3}\)

    Simplifique:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    Responda
    1. 4
    2. 14

    Sabemos que todo número positivo tem duas raízes quadradas e o sinal radical indica o positivo. Nós escrevemos\(\sqrt{100)=10\). Se quisermos encontrar a raiz quadrada negativa de um número, colocamos um negativo na frente do sinal radical. Por exemplo,\(-\sqrt{100)=-10\). Lemos\(-\sqrt{100)\) como “o oposto da raiz quadrada de 10”.

    Exercício\(\PageIndex{4}\)

    Simplifique:

    1. \(-\sqrt{9}\)
    2. \(-\sqrt{144}\)
    Responda
    1. \[\begin{array} {ll} {} &{-\sqrt{9}} \\ {\text {The negative is in front of the radical sign.}} &{-3} \end{array}\]
    2. \[\begin{array} {ll} {} &{-\sqrt{144}} \\ {\text {The negative is in front of the radical sign.}} &{-12} \end{array}\]
    Exercício\(\PageIndex{5}\)

    Simplifique:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    Responda
    1. −2
    2. −15
    Exercício\(\PageIndex{6}\)

    Simplifique:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    Responda
    1. −9
    2. −10

    Identifique números inteiros, números racionais, números irracionais e números reais

    Já descrevemos números como números de contagem s, números inteiros s e números inteiros. Qual é a diferença entre esses tipos de números?

    \[\begin{array} { l l } { \text { Counting numbers } } & { 1,2,3,4 , \ldots } \\ { \text { Whole numbers } } & { 0,1,2,3,4 , \ldots } \\ { \text { Integers } } & { \dots - 3 , - 2 , - 1,0,1,2,3 , \ldots } \end{array}\]

    Que tipo de números obteríamos se começássemos com todos os inteiros e depois incluíssemos todas as frações? Os números que teríamos formam o conjunto de números racionais. Um número racional é um número que pode ser escrito como uma proporção de dois inteiros.

    NÚMERO RACIONAL

    Um número racional é um número da forma\(\dfrac{p}{q}\), onde p e q são números inteiros e\(q \neq 0\)

    Um número racional pode ser escrito como a proporção de dois números inteiros.

    Todas as frações assinadas, como\(\dfrac{4}{5}\),,\(-\dfrac{7}{8}\),\(\dfrac{13}{4}\),\(-\dfrac{20}{3}\) são números racionais. Cada numerador e cada denominador são um número inteiro.

    Os números inteiros são números racionais? Para decidir se um número inteiro é um número racional, tentamos escrevê-lo como uma proporção de dois inteiros. Cada número inteiro pode ser escrito como uma proporção de números inteiros de várias maneiras. Por exemplo, 3 é equivalente a\(\dfrac{3}{1}\),\(-\dfrac{6}{2}\),\(\dfrac{9}{3}\),\(\dfrac{12}{4}\),\(-\dfrac{15}{5} \ldots\)

    Uma maneira fácil de escrever um número inteiro como uma proporção de números inteiros é escrevê-lo como uma fração com o denominador um.

    \[3 = \frac { 3 } { 1 } \quad - 8 = - \frac { 8 } { 1 } \quad 0 = \frac { 0 } { 1 }\]

    Como qualquer número inteiro pode ser escrito como a proporção de dois inteiros, todos os números inteiros são números racionais! Lembre-se de que os números contados e os números inteiros também são inteiros e, portanto, eles também são racionais.

    E quanto aos decimais? Eles são racionais? Vamos dar uma olhada em alguns para ver se podemos escrever cada um deles como a proporção de dois números inteiros.

    Já vimos que números inteiros são números racionais. O número inteiro\(−8\) pode ser escrito como decimal\(−8.0\). Então, claramente, alguns decimais são racionais.

    Pense no decimal\(7.3\). Podemos escrevê-lo como uma proporção de dois números inteiros? Porque\(7.3\) significa que\(7\dfrac{3}{10}\) podemos escrevê-lo como uma fração imprópria,\(\dfrac{73}{10}\). Então\(7.3\) é a proporção dos números inteiros\(73\)\(10\) e. É um número racional.

    Em geral, qualquer decimal que termine após um número de dígitos (como\(7.3\) ou\(−1.2684\)) é um número racional. Podemos usar o valor posicional do último dígito como denominador ao escrever o decimal como uma fração.

    Exercício\(\PageIndex{7}\)

    Escreva como a proporção de dois números inteiros:

    1. −27
    2. 7.31
    Responda
    1. \[\begin{array} {ll} {} &{-27} \\ {\text {Write it as a fraction with denominator 1.}} &{\dfrac{-27}{1}} \end{array}\]
    2. \[\begin{array} {ll} {} &{7.31} \\ {\text {Write is as a mixed number. Remember.}} &{} \\ {\text {7 is the whole number and the decimal}} &{7\dfrac{31}{100}} \\ {\text {part, 0.31, indicates hundredths.}} &{} \\ {\text{Convert to an improper fraction.}} &{\dfrac{731}{100}} \end{array}\]

    Então, vemos que −27 e 7,31 são ambos números racionais, pois podem ser escritos como a proporção de dois inteiros.

    Exercício\(\PageIndex{8}\)

    Escreva como a proporção de dois números inteiros:

    1. −24
    2. 3,57
    Responda
    1. \(\dfrac{-24}{1}\)
    2. \(\dfrac{357}{100}\)
    Exercício\(\PageIndex{9}\)

    Escreva como a proporção de dois números inteiros:

    1. −19
    2. 8.41
    Responda
    1. \(\dfrac{-19}{1}\)
    2. \(\dfrac{841}{100}\)
    Vejamos a forma decimal dos números que sabemos serem racionais.

    Vimos que todo inteiro é um número racional, já que\(a = \dfrac{a}{1}\) para qualquer inteiro,\(a\). Também podemos transformar qualquer número inteiro em decimal adicionando um ponto decimal e um zero.

    \[\begin{array} { l l l l l l l } { \text { Integer } } & { - 2 } & { - 1 } & { 0 } & { 1 } & { 2 } & { 3 } \\ { \text { Decimal form } } & { - 2.0 } & { - 1.0 } & { 0.0 } & { 1.0 } & { 2.0 } & { 3.0 } \\ { } & { \text { These decimal numbers stop. } } \end{array}\]

    Também vimos que cada fração é um número racional. Veja a forma decimal das frações que consideramos acima.

    \[\begin{array} { l l l l } { \text { Ratio of integers } } & { \frac { 4 } { 5 } } & { - \frac { 7 } { 8 } } & { \frac { 13 } { 4 } } & { - \frac { 20 } { 3 } } \\ { \text { The decimal form } } & { 0.8 } & { - 0.875 } & { 3.25 } & { - 6.666 \dots } \\ { } & { } & { } & { - 6.\overline{6} } \\ { } & { \text { These decimal either stop or repeat. } } \end{array}\]

    O que esses exemplos nos dizem?

    Cada número racional pode ser escrito como uma proporção de números inteiros\(\dfrac{p}{q}\), (, onde p e q são números inteiros e\(q\neq 0\)) e como um decimal que para ou se repete.

    Aqui estão os números que analisamos acima, expressos como uma proporção de números inteiros e como um decimal:

    Frações Números inteiros
    Número \(\frac{4}{5}\) \(\frac{7}{8}\) \(\frac{13}{4}\) \(-\frac{20}{3}\) −2 −1 0 1 2 3
    Proporção de números inteiros \(\frac{4}{5}\) \(\frac{7}{8}\) \(\frac{13}{4}\) \(-\frac{20}{3}\) \(-\frac{2}{1}\) \(-\frac{1}{1}\) \(\frac{0}{1}\) \(\frac{1}{1}\) \(\frac{2}{1}\) \(\frac{3}{1}\)
    Forma decimal 0,8 −0,875 3,25 \(−6.\overline{6}\) −2,0 −1,0 0,0 1,0 2.0 3,0
    Tabela\(\PageIndex{1}\)
    NÚMERO RACIONAL

    Um número racional é um número da forma\(\frac{p}{q}\), onde p e q são números inteiros e\(q\neq 0\)

    Sua forma decimal para ou se repete.

    Existem números decimais que não param nem se repetem? Sim!

    O número\(\pi\) (a letra grega pi, pronunciada “torta”), que é muito importante na descrição de círculos, tem uma forma decimal que não para nem se repete.

    \[\pi =3.141592654\ldots\]

    Podemos até criar um padrão decimal que não pare nem se repita, como

    \[2.01001000100001\ldots\]

    Números cuja forma decimal não para ou se repete não podem ser escritos como uma fração de números inteiros. Chamamos esses números de irracionais.

    NÚMERO IRRACIONAL

    Um número irracional é um número que não pode ser escrito como a proporção de dois inteiros.

    Sua forma decimal não para e não se repete.

    Vamos resumir um método que podemos usar para determinar se um número é racional ou irracional.

    RACIONAL OU IRRACIONAL?

    Se a forma decimal de um número

    • repete ou para, o número é racional.
    • não repete e não para, o número é irracional.
    Exercício\(\PageIndex{10}\)

    Dada a\(0.58\overline{3}, 0.47, 3.605551275\ldots\) lista de números

    1. números racionais
    2. números irracionais.
    Responda
    1. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{\text{The 3 repeats in }0.58\overline{3}.} \\ {} &{\text {The decimal 0.47 stops after the 7.}}\\ {} &{\text {So } 0.58\overline{3} \text{ and } 0.47 \text{are rational}} \end{array}\]
    2. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{3.605551275\ldots\text{has no repeating block of}} \\ {} &{\text {digits and it does not stop.}}\\ {} &{\text {So } 3.605551275\ldots \text{ is irrational.}} \end{array}\]
    Exercício\(\PageIndex{11}\)

    Para os números fornecidos, liste o

    1. números racionais
    2. números irracionais:\(0.29, 0.81\overline{6}, 2.515115111….\)
    Responda
    1. \(0.29, 0.81\overline{6}\)
    2. \(2.515115111….\)
    Exercício\(\PageIndex{12}\)

    Para os números fornecidos, liste o

    1. números racionais
    2. números irracionais:\(2.6\overline{3}, 0.125, 0.418302…\)
    Responda
    1. \(2.6\overline{3}, 0.125\)
    2. \(0.418302…\)
    Exercício\(\PageIndex{13}\)

    Para cada número fornecido, identifique se é racional ou irracional:

    1. \(\sqrt{36}\)
    2. \(\sqrt{44}\)
    Responda
    1. Reconheça que 36 é um quadrado perfeito, já que\(6^{2} = 36\). Então\(\sqrt{36} = 6\), portanto,\(\sqrt{36}\) é racional.
    2. Lembre-se disso\(6^{2} = 36\) e\(7^{2} = 49\), portanto, não\(44\) é um quadrado perfeito. Portanto, a forma decimal de nunca se\(\sqrt{44}\) repetirá e nunca parará, então\(\sqrt{44}\) é irracional.
    Exercício\(\PageIndex{14}\)

    Para cada número fornecido, identifique se é racional ou irracional:

    1. \(\sqrt{81}\)
    2. \(\sqrt{17}\)
    Responda
    1. racional
    2. irracional
    Exercício\(\PageIndex{15}\)

    Para cada número fornecido, identifique se é racional ou irracional:

    1. \(\sqrt{116}\)
    2. \(\sqrt{121}\)
    Responda
    1. irracional
    2. racional

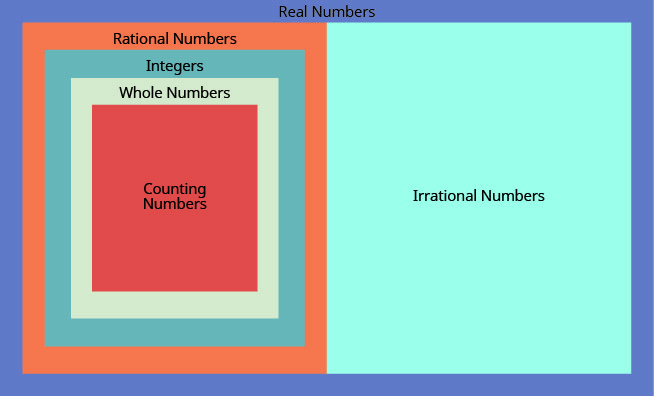
    Vimos que todos os números contados são números inteiros, todos os números inteiros são números inteiros e todos os números inteiros são números racionais. Os números irracionais são números cuja forma decimal não para e não se repete. Quando juntamos os números racionais e os números irracionais, obtemos o conjunto dos números reais s.

    NÚMERO REAL

    Um número real é um número que é racional ou irracional.

    Todos os números que usamos na álgebra elementar são números reais. \(\PageIndex{3}\)A figura ilustra como os conjuntos de números que discutimos nesta seção se encaixam.

    Esta figura consiste em um diagrama de Venn. Para começar, há um grande retângulo marcado com números reais. A metade direita do retângulo consiste em números irracionais. A metade esquerda consiste em números racionais. Dentro do retângulo de números racionais, existem números inteiros..., menos 2, menos 1, 0, 1, 2,... Dentro do retângulo de números inteiros, existem números inteiros 0, 1, 2, 3,... Dentro do retângulo de números inteiros, há números de contagem 1, 2, 3,...
    Figura\(\PageIndex{3}\): Este gráfico mostra os conjuntos de números que compõem o conjunto de números reais. O termo “números reais” parece estranho para você? Existem números que não sejam “reais” e, em caso afirmativo, quais poderiam ser?

    Podemos simplificar\(\sqrt{-25}\)? Existe um número cujo quadrado é\(−25\)?

    \[(\quad)^{2}=−25?\]

    Nenhum dos números com os quais lidamos até agora tem um quadrado que seja\(−25\). Por quê? Qualquer número positivo ao quadrado é positivo. Qualquer número negativo ao quadrado é positivo. Então, dizemos que não há um número real igual\(\sqrt{-25}\) a.

    A raiz quadrada de um número negativo não é um número real.

    Exercício\(\PageIndex{16}\)

    Para cada número fornecido, identifique se é um número real ou não:

    1. \(\sqrt{-169}\)
    2. \(-\sqrt{64}\)
    Responda
    1. Não existe um número real cujo quadrado seja\(−169\). Portanto, não\(\sqrt{-169}\) é um número real.
    2. Como o negativo está na frente do radical,\(-\sqrt{64}\) é\(−8\), já que\(−8\) é um número real,\(-\sqrt{64}\) é um número real.
    Exercício\(\PageIndex{17}\)

    Para cada número fornecido, identifique se é um número real ou não:

    1. \(\sqrt{-196}\)
    2. \(-\sqrt{81}\)
    Responda
    1. não é um número real
    2. número real
    Exercício\(\PageIndex{18}\)

    Para cada número fornecido, identifique se é um número real ou não:

    1. \(-\sqrt{49}\)
    2. \(\sqrt{-121}\)
    Responda
    1. número real
    2. não é um número real
    Exercício\(\PageIndex{19}\)

    Dados os números\(−7, \frac{14}{5}, 8, \sqrt{5}, 5.9, \sqrt{64}\), liste os

    1. números inteiros
    2. inteiros
    3. números racionais
    4. números irracionais
    5. números reais
    Responda
    1. Lembre-se de que os números inteiros são 0, 1, 2, 3,... e 8 é o único número inteiro fornecido.
    2. Os números inteiros são os números inteiros, seus opostos e 0. Portanto, o número inteiro 8 é um número inteiro e −7 é o oposto de um número inteiro, então também é um número inteiro. Além disso, observe que 64 é o quadrado de 8 então\(-\sqrt{64} = -8\). Então, os números inteiros são\(−7, 8, \sqrt{64}\).
    3. Como todos os números inteiros são racionais, então\(-7, 8, -\sqrt{64}\) são racionais. Os números racionais também incluem frações e decimais que se repetem ou param, portanto\(\frac{14}{5}\) e\(5.9\) são racionais. Portanto, a lista de números racionais é\(−7, \frac{14}{5}, 8, 5.9, \sqrt{64}\)
    4. Lembre-se de que 5 não é um quadrado perfeito, então\(\sqrt{5}\) é irracional.
    5. Todos os números listados são números reais.
    Exercício\(\PageIndex{20}\)

    Para os números fornecidos, liste os

    1. números inteiros
    2. inteiros
    3. números racionais
    4. números irracionais
    5. números reais:\(−3, -\sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    Responda
    1. \(4, \sqrt{49}\).
    2. \(−3, 4, \sqrt{49}\)
    3. \(−3, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    4. \( -\sqrt{2}\)
    5. \(−3, \sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    Exercício\(\PageIndex{21}\)

    Para os números fornecidos, liste os

    1. números inteiros
    2. inteiros
    3. números racionais
    4. números irracionais
    5. números reais:\(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)
    Responda
    1. \(6, \sqrt{121}\).
    2. \(−\sqrt{25}, −1, 6, \sqrt{121}\)
    3. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}\)
    4. \(2.041975…\)
    5. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)

    Localize frações na reta numérica

    A última vez que olhamos para a reta numérica, ela tinha apenas números inteiros positivos e negativos. Agora queremos incluir a fração s e decimais nela.

    Nota

    Fazer a atividade de Matemática Manipulativa “Linha Numérica Parte 3” ajudará você a desenvolver uma melhor compreensão da localização das frações na reta numérica.

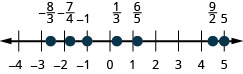
    Vamos começar com frações e localizar\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) e\(\frac{8}{3}\) na reta numérica.

    Começaremos com os números inteiros 3 e −5. porque eles são os mais fáceis de traçar. Veja a Figura\(\PageIndex{4}\).

    As frações apropriadas listadas são\(\frac{1}{5}\text{ and } -\frac{4}{5}\). Sabemos que a fração adequada\(\frac{1}{5}\) tem valor menor que um e, portanto, estaria localizada entre 0 e 1. O denominador é 5, então dividimos a unidade de 0 a 1 em 5 partes iguais\(\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}\). Nós planejamos\(\frac{1}{5}\). Veja a Figura\(\PageIndex{4}\).

    Da mesma forma,\(-\frac{4}{5}\) está entre 0 e −1. Depois de dividir a unidade em 5 partes iguais, traçamos\(-\frac{4}{5}\). Veja a Figura\(\PageIndex{4}\).

    Finalmente, veja as frações impróprias\(\frac{7}{4}, -\frac{9}{2}, \frac{8}{3}\). São frações nas quais o numerador é maior que o denominador. Localizar esses pontos pode ser mais fácil se você alterar cada um deles para um número misto. Veja a Figura\(\PageIndex{4}\).

    \[\frac { 7 } { 4 } = 1 \frac { 3 } { 4 } \quad - \frac { 9 } { 2 } = - 4 \frac { 1 } { 2 } \quad \frac { 8 } { 3 } = 2 \frac { 2 } { 3 }\]

    A figura\(\PageIndex{4}\) mostra a reta numérica com todos os pontos traçados.

    Há uma linha numérica mostrada que vai de menos 6 a 6 positivo. Da esquerda para a direita, os números marcados são menos 5, menos 9/2, menos 4/5, 1/5, 4/5, 8/3 e 3. O número negativo 9/2 está a meio caminho entre menos 5 e menos 4. O número negativo 4/5 está ligeiramente à direita de menos 1. O número 1/5 está ligeiramente à direita de 0. O número 4/5 está ligeiramente à esquerda de 1. O número 8/3 está entre 2 e 3, mas um pouco mais próximo de 3.
    Figura\(\PageIndex{4}\)
    Exercício\(\PageIndex{22}\)

    Localize e rotule o seguinte em uma linha numérica:\(4, \frac{3}{4}, -\frac{1}{4}, -3, \frac{6}{5}, -\frac{5}{2}\)\(\frac{7}{3}\) e.

    Responda

    Localize e plote os números inteiros, 4, −3.

    Localize\(\frac{3}{4}\) primeiro a fração adequada. A fração\(\frac{3}{4}\) está entre 0 e 1. Divida a distância entre 0 e 1 em quatro partes iguais e, em seguida, traçamos\(\frac{3}{4}\). Trama semelhante\(-\frac{1}{4}\).

    Agora localize as frações impróprias\(\frac{6}{5}\),\(-\frac{5}{2}\),\(\frac{7}{3}\). É mais fácil plotá-los se os convertermos em números mistos e depois plotá-los conforme descrito acima:\(\frac{6}{5} = 1\frac{1}{5}\),\(-\frac{5}{2} = -2\frac{1}{2}\),\(\frac{7}{3} = 2\frac{1}{3}\).

    Há uma linha numérica mostrada que vai de menos 6 a 6 positivo. Da esquerda para a direita, os números marcados são menos 3, menos 5/2, menos 1/4, 3/4, 6/5, 7/3 e 4. O número negativo 5/2 está a meio caminho entre menos 3 e menos 2. O número menos 1/4 está ligeiramente à esquerda de 0. O número 3/4 está ligeiramente à esquerda de 1. O número 6/5 está ligeiramente à direita de 1. O número 7/3 está entre 2 e 3, mas um pouco mais próximo de 2.

    Exercício\(\PageIndex{23}\)

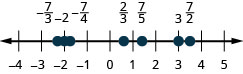
    Localize e rotule o seguinte em uma linha numérica:\(-1, \frac{1}{3}, \frac{6}{5}, -\frac{7}{4}, \frac{9}{2}, 5\)\(-\frac{8}{3}\) e.

    Responda

    Há uma linha numérica mostrada que vai de menos 4 a 5 positivo. Da esquerda para a direita, os números marcados são menos 8/3, menos 7/4, menos 1, 1/3, 6/5, 9/2 e 5. O número negativo 8/3 está entre menos 3 e menos 2, mas um pouco mais próximo de menos 3. O número negativo 7/4 está ligeiramente à direita de menos 2. O número 1/3 está ligeiramente à direita de 0. O número 6/5 está ligeiramente à direita de 1. O número 9/2 está a meio caminho entre 4 e 5.

    Exercício\(\PageIndex{24}\)

    Localize e rotule o seguinte em uma linha numérica:\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\)\(\frac{8}{3}\) e.

    Responda

    Há uma linha numérica mostrada que vai de menos 4 a 5 positivo. Da esquerda para a direita, os números marcados são menos 7/3, menos 2, menos 7/4, 2/3, 7/5, 3 e 7/2. O número negativo 7/3 está entre menos 3 e menos 2, mas um pouco mais próximo de menos 2. O número negativo 7/4 está ligeiramente à direita de menos 2. O número 2/3 está ligeiramente à esquerda de 1. O número 7/5 está entre 1 e 2, mas mais próximo de 1. O número 7/2 está a meio caminho entre 3 e 4.

    No Exercício\(\PageIndex{25}\), usaremos os símbolos de desigualdade para ordenar frações. Nos capítulos anteriores, usamos a linha numérica para ordenar números.

    • \(a < b\)“a é menor que b” quando a está à esquerda de b na reta numérica
    • \(a > b\)“a é maior que b” quando a está à direita de b na reta numérica

    À medida que avançamos da esquerda para a direita em uma reta numérica, os valores aumentam.

    Exercício\(\PageIndex{25}\)

    Ordene cada um dos seguintes pares de números, usando\(<\) ou\(>\). Pode ser útil consultar a Figura\(\PageIndex{5}\).

    1. \(−\frac{2}{3}\text{___}-1\)
    2. \(−3\frac{1}{2}\text{___}-3\)
    3. \(−\frac{3}{4}\text{___}-\frac{1}{4}\)
    4. \(−2\text{___}-\frac{8}{3}\)
    Há uma linha numérica mostrada que vai de menos 4 a positivo 4. Da esquerda para a direita, os números marcados são menos 3 e 1/2, menos 3, menos 8/3, menos 2, menos 1, menos 3/4, menos 2/3 e menos 1/4. O número negativo 3 e 1/2 está entre menos 4 e menos 3 O número negativo 8/3 está entre menos 3 e menos 2, mas mais próximo de menos 3. Os números menos 3/4, menos 2/3 e menos 1/4 estão todos entre menos 1 e 0.
    Figura\(\PageIndex{5}\)
    Responda

    Tenha cuidado ao pedir números negativos.

    1. \(\begin{array} { r r } { } & { - \frac { 2 } { 3 } \text{ ___ } -1 } \\ { - \frac { 2 } { 3 } \text { is to the right of } - 1 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
    2. \(\begin{array} { r r } { } & { - 3\frac { 1 } { 2 } \text{ ___ } -3 } \\ { - 3\frac { 1 } { 2 } \text { is to the right of } - 3 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
    3. \(\begin{array} { r r } { } & { - \frac { 3 } { 4 } \text{ ___ } -\frac{1}{4} } \\ { - \frac { 3 } { 4 } \text { is to the right of } - \frac{1}{4} \text { on the number line. } } & { - \frac{3}{4} < - \frac{1}{4} } \end{array}\)
    4. \(\begin{array} { r r } { } & { - \-2 \text{ ___ } -\frac{8}{3} } \\ { -2 \text { is to the right of } - \frac{8}{3} \text { on the number line. } } & { -2 > -\frac{8}{3} } \end{array}\)
    Exercício\(\PageIndex{26}\)

    Ordene cada um dos seguintes pares de números, usando\(<\) ou\(>\).

    1. \(−\frac{1}{3}\text{___}-1\)
    2. \(−1\frac{1}{2}\text{___}-2\)
    3. \(−\frac{2}{3}\text{___}-\frac{1}{3}\)
    4. \(−3\text{___}-\frac{7}{3}\)
    Responda
    1. \(>\)
    2. \(>\)
    3. \(<\)
    4. \(<\)
    Exercício\(\PageIndex{27}\)

    Ordene cada um dos seguintes pares de números, usando\(<\) ou\(>\).

    1. \(−1\text{___}-\frac{2}{3}\)
    2. \(−2\frac{1}{4}\text{___}-2\)
    3. \(−\frac{3}{5}\text{___}-\frac{4}{5}\)
    4. \(−4\text{___}-\frac{10}{3}\)
    Responda
    1. \(<\)
    2. \(<\)
    3. \(>\)
    4. \(<\)

    Localize números decimais na reta numérica

    Como decimais são formas de frações, localizar decimais na reta numérica é semelhante a localizar frações na reta numérica.

    Exercício\(\PageIndex{28}\)

    Localize 0,4 na linha numérica.

    Responda

    Uma fração adequada tem valor menor que um. O número decimal\(0.4\) é equivalente a\(\frac{4}{10}\) uma fração própria, então\(0.4\) está localizado entre 0 e 1. Em uma reta numérica, divida o intervalo entre 0 e 1 em 10 partes iguais. Agora rotule as peças\(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0\). Escrevemos 0 como 0,0 e 1 e 1,0, para que os números estejam consistentemente em décimos. Finalmente, marque\(0.4\) na linha numérica. Veja a Figura\(\PageIndex{6}\).

    Há uma linha numérica mostrada que vai de 0,0 a 1. O único ponto dado é 0,4, que está entre 0,3 e 0,5.
    Figura\(\PageIndex{6}\)
    Exercício\(\PageIndex{29}\)

    Localize na linha numérica: 0,6.

    Responda

    Há uma linha numérica mostrada que vai de 0,0 a 1. O único ponto dado é 0,6, que está entre 0,5 e 0,7.

    Exercício\(\PageIndex{30}\)

    Localize na linha numérica: 0,9.

    Responda

    Há uma linha numérica mostrada que vai de 0,0 a 1. O único ponto dado é 0,9, que está entre 0,8 e 1.

    Exercício\(\PageIndex{31}\)

    Localize\(−0.74\) na linha numérica.

    Responda

    O decimal (−0,74\) é equivalente a\(-\frac{74}{100}\), então está localizado entre 0 e −1. Em uma reta numérica, marque e rotule os centésimos no intervalo entre 0 e −1. Veja a Figura\(\PageIndex{7}\).

    Há uma linha numérica mostrada que vai de menos 1,00 a 0,00. O único ponto dado é menos 0,74, que está entre menos 0,8 e menos 0,7.
    Figura\(\PageIndex{7}\)
    Exercício\(\PageIndex{32}\)

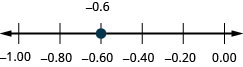
    Localize na reta numérica: −0,6.

    Responda

    Há uma linha numérica mostrada que vai de menos 1,00 a 0,00. O único ponto dado é menos 0,6, que está entre menos 0,8 e menos 0,4.

    Exercício\(\PageIndex{33}\)

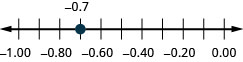
    Localize na reta numérica: −0,7.

    Responda

    Há uma linha numérica mostrada que vai de menos 1,00 a 0,00. O único ponto dado é menos 0,7, que está entre menos 0,8 e menos 0,6.

    Qual é maior, 0,04 ou 0,40? Se você pensa nisso como dinheiro, sabe que $0,40 (quarenta centavos) é maior que $0,04 (quatro centavos). Então,\(0.40 > 0.04\)

    Novamente, podemos usar a linha numérica para ordenar números.

    • \(a < b\)“a é menor que b” quando a está à esquerda de b na reta numérica
    • \(a > b\)“a é maior que b” quando a está à direita de b na reta numérica

    Onde estão 0,04 e 0,40 localizados na reta numérica? Veja a Figura\(\PageIndex{8}\).

    Há uma linha numérica mostrada que vai de menos 0,0 a 1,0. Da esquerda para a direita, estão marcados os pontos 0,04 e 0,4. O ponto 0,04 está entre 0,0 e 0,1. O ponto 0,4 está entre 0,3 e 0,5.
    Figura\(\PageIndex{8}\)

    Vemos que 0,40 está à direita de 0,04 na reta numérica. Essa é outra forma de demonstrar isso\(0.40 > 0.04\).

    Como 0,31 se compara a 0,308? Isso não se traduz em dinheiro para facilitar a comparação. Mas se convertermos 0,31 e 0,308 em frações, podemos dizer qual é maior.

      0,31 0,308
    Converta em frações. \(\frac{31}{100}\) \(\frac{308}{1000}\)
    Precisamos de um denominador comum para compará-los. . .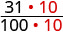
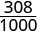      \(\frac{310}{1000}\) \(\frac{308}{1000}\)
    Tabela\(\PageIndex{2}\)

    Porque\(310 > 308\), nós sabemos disso\(\frac{310}{1000} > \frac{308}{1000}\). Portanto,\(0.31 > 0.308\).

    Observe o que fizemos na conversão\(0.31\) para uma fração — começamos com a fração\(\frac{31}{100}\) e terminamos com a fração equivalente. A\(\frac{310}{1000}\) conversão de\(\frac{310}{1000}\) volta para um decimal dá 0,310. Portanto, 0,31 é equivalente a 0,310. Escrever zeros no final de um decimal não altera seu valor!

    \[\frac { 31 } { 100 } = \frac { 310 } { 1000 } \quad \text { and } \quad 0.31 = 0.310\]

    Dizemos que 0,31 e 0,310 são decimais equivalentes.

    DECIMAIS EQUIVALENTES

    Dois decimais são equivalentes se forem convertidos em frações equivalentes.

    Usamos decimais equivalentes quando pedimos decimais.

    As etapas que tomamos para ordenar os decimais estão resumidas aqui.

    ORDENE DECIMAIS.
    1. Escreva os números um abaixo do outro, alinhando os pontos decimais.
    2. Verifique se os dois números têm o mesmo número de dígitos. Caso contrário, escreva zeros no final daquele com menos dígitos para fazer com que coincidam.
    3. Compare os números como se fossem números inteiros.
    4. Ordene os números usando o sinal de desigualdade apropriado.
    Exercício\(\PageIndex{34}\)

    Faça\(0.64 \text{ ___ } 0.6\) o pedido usando\(<\) ou\(>\).

    Responda

    \(\begin{array} { ll } { \text {Write the numbers one under the other, } } &{0.64} \\ { \text {lining up the decimal points. } } &{0.6} \\ \\ { \text {Add a zero to 0.6 to make it a decimal } } &{0.64} \\ {\text{with 2 decimal places.}} &{0.60} \\ {\text{Now they are both hundredths.}} &{} \\ \\ {\text{64 is greater than 60.}} &{64 > 60} \\ \\ {\text{64 hundredths is greater than 60 hundredths.}} &{0.64 > 0.60} \\ \\ {} &{0.64 > 0.6}\end{array}\)

    Exercício\(\PageIndex{35}\)

    Ordene cada um dos seguintes pares de números, usando\(<\) ou\(>\):\(0.42 \text{ ___ } 0.4\).

    Responda

    \(>\)

    Exercício\(\PageIndex{36}\)

    Ordene cada um dos seguintes pares de números, usando\(<\) ou\(>\):\(0.18 \text{ ___ } 0.1\).

    Responda

    \(>\)

    Exercício\(\PageIndex{37}\)

    Faça\(0.83 \text{ ___ } 0.803\) o pedido usando\(<\) ou\(>\).

    Responda

    \(\begin{array} { ll } {} &{0.83\text{ ___ }0.803} \\ \\{ \text {Write the numbers one under the other, } } &{0.83} \\ { \text {lining up the decimal points. } } &{0.803} \\ \\ { \text {They do not have the same number of} } &{0.830} \\ {\text{digits.}} &{0.803} \\ {\text{Write one zero at the end of 0.83.}} &{} \\ \\ {\text{Since 830 > 803, 830 hundredths is}} &{0.830 > 0.803} \\ {\text{greater than 803 thousandths.}} &{}\\ \\ {} &{0.83 > 0.803}\end{array}\)

    Exercício\(\PageIndex{38}\)

    Ordene cada um dos seguintes pares de números, usando\(<\) ou\(>\):\(0.76 \text{ ___ } 0.706\).

    Responda

    \(>\)

    Exercício\(\PageIndex{39}\)

    Ordene cada um dos seguintes pares de números, usando\(<\) ou\(>\):\(0.305 \text{ ___ } 0.35\).

    Responda

    \(<\)

    Quando ordenamos números decimais negativos, é importante lembrar como ordenar números inteiros negativos. Lembre-se de que números maiores estão à direita na reta numérica. Por exemplo, como −2 está à direita de -3 na reta numérica, sabemos disso\(−2>−3\). Da mesma forma, números menores ficam à esquerda na linha numérica. Por exemplo, como −9 está à esquerda de −6 na reta numérica, sabemos disso\(−9<−6\). Veja a Figura\(\PageIndex{9}\).

    Há uma linha numérica mostrada que vai de menos 10 a 0. Não há pontos dados e os hashmarks existem em cada número inteiro entre menos 10 e 0.
    Figura\(\PageIndex{9}\)

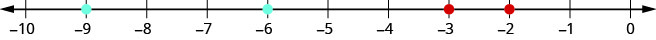
    Se ampliássemos o intervalo entre 0 e −1, conforme mostrado no Exercício\(\PageIndex{40}\), veríamos da mesma forma que\(−0.2>−0.3\)\(−0.9<−0.6\) e.

    Exercício\(\PageIndex{40}\)

    Use\(<\) ou\(>\) para fazer o pedido\(−0.1\text{ ___ }−0.8\).

    Responda

    \(\begin{array} { ll } {} &{-0.1 \text{ ___ } -0.8} \\ \\ { \text { Write the numbers one under the other, lining up the } } &{-0.1} \\ { \text { decimal points. } } &{-0.8} \\ { \text { They have the same number of digits. } } &{} \\ \\ { \text { since } - 1 > - 8 , - 1 \text { tenth is greater than } - 8 \text { tenths. } } &{-0.1 > -0.8} \end{array}\)

    Exercício\(\PageIndex{41}\)

    Peça o seguinte par de números, usando\(<\) ou\(>\):\(−0.3\text{ ___ }−0.5\).

    Responda

    \(>\)

    Exercício\(\PageIndex{42}\)

    Peça o seguinte par de números, usando\(<\) ou\(>\):\(−0.6\text{ ___ }−0.7\).

    Responda

    \(>\)

    Conceitos-chave

    • A notação de raiz quadrada
      \(\sqrt{m}\) é lida como “a raiz quadrada de”\(m\). Se\(m = n^{2}\), então\(\sqrt{m} = n\), para\(n \geq 0\).
    • Ordenar decimais
      1. Escreva os números um abaixo do outro, alinhando os pontos decimais.
      2. Verifique se os dois números têm o mesmo número de dígitos. Caso contrário, escreva zeros no final daquele com menos dígitos para fazer com que coincidam.
      3. Compare os números como se fossem números inteiros.
      4. Ordene os números usando o sinal de desigualdade apropriado.

    A prática leva à perfeição

    Simplifique expressões com raízes quadradas

    Nos exercícios a seguir, simplifique.