1.5: Multiplique e divida números inteiros
- Page ID
- 184428
Ao final desta seção, você poderá:
- Multiplique números inteiros
- Divida números inteiros
- Simplifique expressões com números inteiros
- Avalie expressões variáveis com números inteiros
- Traduza frases em inglês para expressões algébricas
- Use números inteiros em aplicativos
Uma introdução mais completa aos tópicos abordados nesta seção pode ser encontrada no capítulo Pré-álgebra, Inteiros.
Multiplique números inteiros
Como a multiplicação é uma abreviatura matemática para adição repetida, nosso modelo pode ser facilmente aplicado para mostrar a multiplicação de números inteiros. Vamos dar uma olhada nesse modelo concreto para ver quais padrões observamos. Usaremos os mesmos exemplos que usamos para adição e subtração. Aqui, usaremos o modelo apenas para nos ajudar a descobrir o padrão.
Lembramos que isso\(a\cdot b\) significa adicionar\(a,\, b\) horários. Aqui, estamos usando o modelo apenas para nos ajudar a descobrir o padrão.
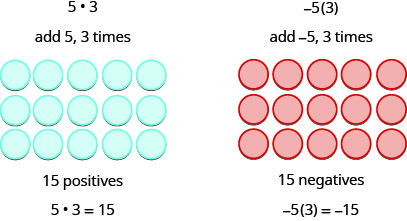
Os próximos dois exemplos são mais interessantes.
O que significa multiplicar\(5\) por\(−3\)? Isso significa subtrair\(5, 3\) vezes. Encarar a subtração como “tirar” significa tirar\(5, 3\) vezes. Mas não há nada para retirar, então começamos adicionando pares neutros no espaço de trabalho. Em seguida, tiramos\(5\) três vezes.
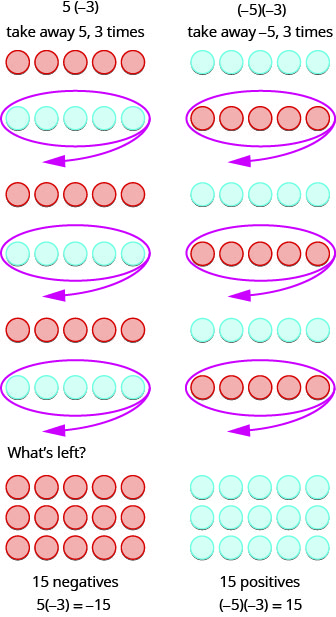
Em resumo:
\[\begin{array} {ll} {5 \cdot 3 = 15} &{-5(3) = -15} \\ {5(-3) = -15} &{(-5)(-3) = 15} \end{array}\]
Observe que, para a multiplicação de dois números assinados, quando:
- os sinais são os mesmos, o produto é positivo.
- os sinais são diferentes, o produto é negativo.
Vamos juntar tudo isso no gráfico abaixo.
Para multiplicação de dois números assinados:
| Mesmos sinais | Produto | Exemplo |
|---|---|---|
| Dois pontos positivos | Positivo | \(7\cdot 4 = 28\) |
| Dois negativos | Positivo | \(-8(-6) = 48\) |
| Sinais diferentes | Produto | Exemplo |
|---|---|---|
| Positivos\(\cdot\) negativos | Negativo | \(7(-9) = -63\) |
| \(\cdot\)Positivos negativos | Negativo | \(-5\cdot 10= -50\) |
Multiplique:
- \(-9\cdot 3\)
- \(-2(-5)\)
- \(4(-8)\)
- \(7\cdot 6\)
- Resposta
-
- \[\begin{array} {ll} {} &{-9\cdot 3} \\ {\text{Multiply, noting that the signs are different, so the product is negative.}} &{-27} \end{array}\]
- \[\begin{array} {ll} {} &{-2(-5)} \\ {\text{Multiply, noting that the signs are same, so the product is positive.}} &{10} \end{array}\]
- \[\begin{array} {ll} {} &{4(-8)} \\ {\text{Multiply, with different signs.}} &{-32} \end{array}\]
- \[\begin{array} {ll} {} &{7\cdot 6} \\ {\text{Multiply, with different signs.}} &{42} \end{array}\]
Multiplique:
- \(-6\cdot 8\)
- \(-4(-7)\)
- \(9(-7)\)
- \(5\cdot 12\)
- Resposta
-
- \(-48\)
- \(28\)
- \(-63\)
- \(60\)
Multiplique:
- \(-8\cdot 7\)
- \(-6(-9)\)
- \(7(-4)\)
- \(3\cdot 13\)
- Resposta
-
- \(-56\)
- \(54\)
- \(-28\)
- \(39\)
Quando multiplicamos um número por\(1\), o resultado é o mesmo número. O que acontece quando multiplicamos um número por\(−1\)? Vamos multiplicar um número positivo e depois um número negativo por\(−1\) para ver o que obtemos.
\[\begin{array} {lll} {} &{-1\cdot 4} &{-1(-3)}\\ {\text{Multiply.}} &{-4} &{3} \\ {} &{-4\text{ is the opposite of 4.}} &{3\text{ is the opposite of } -3} \end{array}\]
Cada vez que multiplicamos um número por\(−1\), obtemos o oposto!
MULTIPLICAÇÃO POR −1
\[−1a=−a\]
Multiplicar um número por\(−1\) dá o oposto.
Multiplique:
- \(-1 \cdot 7\)
- \(-1(-11)\)
- Resposta
-
- \[\begin{array} {ll} {} &{-1\cdot 7} \\ {\text{Multiply, noting that the signs are different}} &{-7} \\ {\text{so the product is negative.}} &{-7\text{ is the opposite of 7.}} \end{array}\]
- \[\begin{array} {ll} {} &{-1(-11)} \\ {\text{Multiply, noting that the signs are different}} &{11} \\ {\text{so the product is positive.}} &{11\text{ is the opposite of -11.}} \end{array}\]
Multiplique:
- \(-1\cdot 9\)
- \(-1\cdot(-17)\)
- Resposta
-
- \(-9\)
- \(17\)
Multiplique:
- \(-1\cdot 8\)
- \(-1\cdot(-16)\)
- Resposta
-
- \(-8\)
- \(16\)
Divida números inteiros
E quanto à divisão? A divisão é a operação inversa da multiplicação. Então,\(15\div 3=5\) porque\(5 \cdot 3 = 15\). Em palavras, essa expressão diz que\(15\) pode ser dividido em três grupos de cinco cada, porque somar cinco três vezes dá\(15\). Veja alguns exemplos de multiplicação de números inteiros para descobrir as regras para dividir números inteiros.
\[\begin{array} {ll} {5\cdot 3 = 15\text{ so }15\div 3 = 5} &{-5(3) = -15\text{ so }-15\div 3 = -5} \\ {(-5)(-3) = 15\text{ so }15\div (-3) = -5} &{5(-3) = -15\text{ so }-15\div (-3) = 5} \end{array}\]
A divisão segue as mesmas regras da multiplicação!
Para divisão de dois números assinados, quando:
- os sinais são os mesmos, o quociente é positivo.
- os sinais são diferentes, o quociente é negativo.
E lembre-se de que sempre podemos verificar a resposta de um problema de divisão multiplicando.
Para multiplicação e divisão de dois números assinados:
- Se os sinais forem os mesmos, o resultado será positivo.
- Se os sinais forem diferentes, o resultado será negativo.
| Mesmos sinais | Resultado |
|---|---|
| Dois pontos positivos | Positivo |
| Dois negativos | Positivo |
| Se os sinais forem os mesmos, o resultado será positivo. | |
| Sinais diferentes | Resultado |
|---|---|
| Positivo e negativo | Negativo |
| Negativo e positivo | Negativo |
| Se os sinais forem diferentes, o resultado será negativo. | |
- \(-27\div 3\)
- \(-100\div (-4)\)
- Resposta
-
- \[\begin{array} {ll} {} &{-27 \div 3} \\ {\text{Divide, with different signs, the quotient is}} &{-9} \\ {\text{negative.}} &{} \end{array}\]
- \[\begin{array} {ll} {} &{-100 \div (-4)} \\ {\text{Divide, with signs that are the same the}} &{25} \\ {\text{ quotient is negative.}} &{} \end{array}\]
Divida:
- \(-42\div 6\)
- \(-117\div (-3)\)
- Resposta
-
- \(-7\)
- \(39\)
Divida:
- \(-63\div 7\)
- \(-115\div (-5)\)
- Resposta
-
- \(-9\)
- \(23\)
Simplifique expressões com números inteiros
O que acontece quando há mais de dois números em uma expressão? A ordem das operações ainda se aplica quando os negativos são incluídos. Lembra da minha querida tia Sally?
Vamos tentar alguns exemplos. Simplificaremos expressões que usam todas as quatro operações com números inteiros: adição, subtração, multiplicação e divisão. Lembre-se de seguir a ordem das operações.
Simplifique:
\(7(-2)+4(-7)-6\)
- Resposta
-
\[\begin{array} {ll} {} &{7(-2)+4(-7)-6} \\ {\text{Multiply first.}} &{-14+(-28)-6} \\ {\text{Add.}} &{-42-6} \\{\text{Subtract}} &{-48} \end{array}\]
Simplifique:
\(8(-3)+5(-7)-4\)
- Resposta
-
\(-63\)
Simplifique:
\(9(-3)+7(-8)-1\)
- Resposta
-
\(-84\)
Simplifique:
- \((-2)^{4}\)
- \(-2^{4}\)
- Resposta
-
- \[\begin{array} {ll} {} &{(-2)^{4}} \\ {\text{Write in expanded form.}} &{(-2)(-2)(-2)(-2)} \\ {\text{Multiply}} &{4(-2)(-2)} \\{\text{Multiply}} &{-8(-2)} \\{\text{Multiply}} &{16} \end{array}\]
- \[\begin{array} {ll} {} &{-2^{4}} \\ {\text{Write in expanded form. We are asked to find the opposite of }2^{4}.} &{-(2\cdot 2\cdot 2 \cdot 2)} \\ {\text{Multiply}} &{-(4\cdot 2\cdot 2)} \\{\text{Multiply}} &{-(8\cdot 2)} \\{\text{Multiply}} &{-16} \end{array}\]
Observe a diferença nas partes (1) e (2). Em parte (1), o expoente significa elevar o que está entre parênteses, o\((−2)\) à\(4^{th}\) potência. Na parte (2), o expoente significa elevar apenas o\(2\) à\(4^{th}\) potência e, em seguida, tomar o oposto.
Simplifique:
- \((-3)^{4}\)
- \(-3^{4}\)
- Resposta
-
- \(81\)
- \(-81\)
Simplifique:
- \((-7)^{2}\)
- \(-7^{2}\)
- Resposta
-
- \(49\)
- \(-49\)
O próximo exemplo nos lembra de simplificar primeiro entre parênteses.
Simplifique:
\(12-3(9 - 12)\)
- Resposta
-
\[\begin{array} {llll} {} &{12-3(9 - 12)} \\ {\text{Subtract parentheses first}} &{12-3(-3)} \\ {\text{Multiply.}} &{12-(-9)} \\{\text{Multiply}} &{-(8\cdot 2)} \\{\text{Subtract}} &{21} \end{array}\]
Simplifique:
\(17 - 4(8 - 11)\)
- Resposta
-
\(29\)
Simplifique:
\(16 - 6(7 - 13)\)
- Resposta
-
\(52\)
Simplifique:
\(8(-9)\div (-2)^{3}\)
- Resposta
-
\[\begin{array} {ll} {} &{8(-9)\div(-2)^{3}} \\ {\text{Exponents first}} &{8(-9)\div(-8)} \\ {\text{Multiply.}} &{-72\div (-8)} \\{\text{Divide}} &{9} \end{array}\]
Simplifique:
\(12(-9)\div (-3)^{3}\)
- Resposta
-
\(4\)
Simplifique:
\(18(-4)\div (-2)^{3}\)
- Resposta
-
\(9\)
Simplifique:
\(-30\div 2 + (-3)(-7)\)
- Resposta
-
\[\begin{array} {ll} {} &{-30\div 2 + (-3)(-7)} \\ {\text{Multiply and divide left to right, so divide first.}} &{-15+(-3)(-7)} \\ {\text{Multiply.}} &{-15+ 21} \\{\text{Add}} &{6} \end{array}\]
Simplifique:
\(-27\div 3 + (-5)(-6)\)
- Resposta
-
\(21\)
Simplifique:
\(-32\div 4 + (-2)(-7)\)
- Resposta
-
\(6\)
Avalie expressões variáveis com números inteiros
Lembre-se de que avaliar uma expressão significa substituir um número pela variável na expressão. Agora podemos usar números negativos e números positivos.
Quando\(n=−5\), avalie:
- \(n+1\)
- \(−n+1\).
- Resposta
-
- \[\begin{array} {ll} {} &{n+ 1} \\ {\text{Substitute}-5\text{ for } n} &{-5+1} \\ {\text{Simplify.}} &{-4} \end{array}\]
- \[\begin{array} {ll} {} &{-n+ 1} \\ {\text{Substitute}-5\text{ for } n} &{-(-5)+1} \\ {\text{Simplify.}} &{-4} \\{\text{Add.}} &{6} \end{array}\]
Quando\(n=−8\), avalie:
- \(n+2\)
- \(−n+2\).
- Resposta
-
- \(-6\)
- \(10\)
Quando\(y=−9\), avalie:
- \(y+8\)
- \(−y+8\).
- Resposta
-
- \(-1\)
- \(17\)
Avalie\((x+y)^{2}\) quando\(x = -18\)\(y = 24\) e.
- Resposta
-
\[\begin{array} {ll} {} &{(x+y)^{2}} \\ {\text{Substitute }-18\text{ for }x \text{ and } 24 \text{ for } y} &{(-18 + 24)^{2}} \\ {\text{Add inside parentheses}} &{(6)^{2}} \\{\text{Simplify.}} &{36} \end{array}\]
Avalie\((x+y)^{2}\) quando\(x = -15\)\(y = 29\) e.
- Resposta
-
\(196\)
Avalie\((x+y)^{3}\) quando\(x = -8\)\(y = 10\) e.
- Resposta
-
\(8\)
Avalie\(20 -z \) quando
- \(z = 12\)
- \(z = -12\)
- Resposta
-
- \[\begin{array} {ll} {} &{20 - z} \\ {\text{Substitute }12\text{ for }z.} &{20 - 12} \\ {\text{Subtract}} &{8} \end{array}\]
- \[\begin{array} {ll} {} &{20 - z} \\ {\text{Substitute }-12\text{ for }z.} &{20 - (-12)} \\ {\text{Subtract}} &{32} \end{array}\]
Avalie\(17 - k\) quando
- \(k = 19\)
- \(k = -19\)
- Resposta
-
- \(-2\)
- \(36\)
Avalie\(-5 - b\) quando
- \(b = 14\)
- \(b = -14\)
- Resposta
-
- \(-19\)
- \(9\)
Avalie:
\(2x^{2} + 3x + 8\)quando\(x = 4\).
- Resposta
-
Substituto\(4\) para\(x\). Use parênteses para mostrar a multiplicação.
\[\begin{array} {ll} {} &{2x^{2} + 3x + 8} \\ {\text{Substitute }} &{2(4)^{2} + 3(4) + 8} \\ {\text{Evaluate exponents.}} &{2(16) + 3(4) + 8} \\ {\text{Multiply.}} &{32 + 12 + 8} \\{\text{Add.}} &{52} \end{array}\]
Avalie:
\(3x^{2} - 2x + 6\)quando\(x =-3\).
- Resposta
-
\(39\)
Avalie:
\(4x^{2} - x - 5\)quando\(x = -2\).
- Resposta
-
\(13\)
Traduza frases em expressões com números inteiros
Nosso trabalho anterior traduzindo inglês para álgebra também se aplica a frases que incluem números positivos e negativos.
Traduza e simplifique: a soma de\(8\) e\(−12\), aumentada em\(3\).
- Resposta
-
\[\begin{array} {ll} {} &{\text{the } \textbf{sum} \text{of 8 and -12, increased by 3}} \\ {\text{Translate.}} &{[8 + (-12)] + 3} \\ {\text{Simplify. Be careful not to confuse the}} &{(-4) + 3} \\{\text{brackets with an absolute value sign.}} \\{\text{Add.}} &{-1} \end{array}\]
Traduza e simplifique: a soma de\(9\) e\(−16\), aumentada em\(4\).
- Resposta
-
\((9 + (-16)) + 4 - 3\)
Traduza e simplifique: a soma de\(-8\) e\(−12\), aumentada em\(7\).
- Resposta
-
\((-8 + (-12)) + 7 - 13\)
Quando introduzimos pela primeira vez os símbolos de operação, vimos que a expressão pode ser lida de várias maneiras. Eles estão listados na tabela abaixo.
| \(a−b\) |
|---|
| \ (a−b\)” data-valign="top">\(a\) menos\(b\) a diferença de\(a\) e\(b\) \(b\) subtraída de\(a\) \(b\) menos de\(a\) |
Tenha cuidado para colocar a e b na ordem correta!
Traduza e depois simplifique
- a diferença de\(13\) e\(−21\)
- subtrair\(24\) de\(−19\).
- Responda
-
- \[\begin{array} {ll} {} &{\text{the } \textbf{difference } \text{of 13 and -21}} \\ {\text{Translate.}} &{13 - (-21)} \\ {\text{Simplify.}} &{34} \end{array}\]
- \[\begin{array} {ll} {} &\textbf{subtract }24 \textbf{ from }-19 \\ {\text{Translate.}} &{-19 - 24} \\ {\text{Remember, subtract b from a means }a - b} &{} \\{\text{Simplify.}} &{-43} \end{array}\]
Traduza e simplifique
- a diferença de\(14\) e\(−23\)
- subtrair\(21\) de\(−17\).
- Responda
-
- \(14 - (-23); 37\)
- \(-17 - 21; -38\)
Traduza e simplifique
- a diferença de\(11\) e\(−19\)
- subtrair\(18\) de\(−11\).
- Responda
-
- \(11 - (-19); 30\)
- \(-11 - 18; -29\)
Mais uma vez, nosso trabalho anterior de tradução de inglês para álgebra é transferido para frases que incluem multiplicação e divisão de números inteiros. Lembre-se de que a palavra-chave para multiplicação é “produto” e para divisão é “quociente”.
Traduza para uma expressão algébrica e simplifique, se possível: o produto de\(−2\)\(14\) e.
- Responda
-
\[\begin{array} {ll} {} &{\text{the product of }-2 \text{ and } 14} \\ {\text{Translate.}} &{(-2)(14)} \\{\text{Simplify.}} &{-28} \end{array}\]
Traduza para uma expressão algébrica e simplifique, se possível: o produto de\(−5\)\(12\) e.
- Responda
-
\(-5(12); -60\)
Traduza para uma expressão algébrica e simplifique, se possível: o produto de\(8\)\(-13\) e.
- Responda
-
\(-8(13); -104\)
Traduza para uma expressão algébrica e simplifique, se possível: o quociente de\(−56\)\(−7\) e.
- Responda
-
\[\begin{array} {ll} {} &{\text{the quotient of }-56 \text{ and } -7} \\ {\text{Translate.}} &{-56\div(-7)} \\{\text{Simplify.}} &{8} \end{array}\]
Traduza para uma expressão algébrica e simplifique, se possível: o quociente de\(−63\)\(−9\) e.
- Responda
-
\(-63\div (-9); 7\)
Traduza para uma expressão algébrica e simplifique, se possível: o quociente de\(−72\)\(−9\) e.
- Responda
-
\(-72\div (-9); 8\)
Use números inteiros em aplicativos
Vamos delinear um plano para resolver aplicativos. É difícil encontrar algo se não sabemos o que estamos procurando ou como chamá-lo! Então, quando resolvemos um aplicativo, primeiro precisamos determinar o que o problema está solicitando que encontremos. Em seguida, escreveremos uma frase que forneça as informações para encontrá-la. Vamos traduzir a frase em uma expressão e depois simplificá-la para obter a resposta. Finalmente, resumimos a resposta em uma frase para garantir que ela faça sentido.
Como aplicar uma estratégia para resolver aplicativos com números inteiros
A temperatura em Urbana, Illinois, certa manhã, era de\(11\) graus. No meio da tarde, a temperatura havia caído para\(−9\) graus. Qual foi a diferença das temperaturas da manhã e da tarde?
- Responda
-
Etapa 1. Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas. Etapa 2. Identifique o que devemos encontrar. a diferença das temperaturas da manhã e da tarde Etapa 3. Escreva uma frase que forneça as informações para encontrá-la. a diferença de\(11\) e\(-9\) Etapa 4. Traduza a frase para uma expressão. \(11 - (-9)\) Etapa 5. Simplifique a expressão. \(20\) Etapa 6. Escreva uma frase completa que responda à pergunta. A diferença nas temperaturas foi de 20 graus.
A temperatura em Anchorage, Alasca, em uma manhã, era de\(15\) graus. No meio da tarde, a temperatura havia caído para\(30\) graus abaixo de zero. Qual foi a diferença nas temperaturas da manhã e da tarde?
- Responda
-
A diferença nas temperaturas foi de\(45\) graus.
A temperatura em Denver era de\(−6\) graus na hora do almoço. Ao pôr do sol, a temperatura havia caído para\(−15\) graus. Qual foi a diferença nas temperaturas da hora do almoço e do pôr do sol?
- Responda
-
A diferença nas temperaturas foi de\(9\) graus.
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas
- Identifique o que devemos encontrar.
- Escreva uma frase que forneça as informações para encontrá-la.
- Traduza a frase para uma expressão.
- Simplifique a expressão.
- Responda à pergunta com uma frase completa.
O time de futebol Mustangs recebeu três pênaltis no terceiro quarto. Cada pênalti deu a eles uma perda de quinze jardas. Qual é o número de jardas perdidas?
- Responda
-
Etapa 1. Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas. Etapa 2. Identifique o que devemos encontrar. o número de jardas perdidas Etapa 3. Escreva uma frase que forneça as informações para encontrá-la. três vezes uma penalidade\(15\) de -jarda Etapa 4. Traduza a frase para uma expressão. \(3(-15)\) Etapa 5. Simplifique a expressão. \(-45\) Etapa 6. Escreva uma frase completa que responda à pergunta. A equipe perdeu\(45\) jardas.
Os Bears jogaram mal e tiveram sete pênaltis no jogo. Cada penalidade resultou em uma perda de\(15\) jardas. Qual é o número de jardas perdidas devido às penalidades?
- Responda
-
Os Bears perderam\(105\) jardas.
Bill usa o caixa eletrônico no campus porque é conveniente. No entanto, cada vez que ele o usa, é cobrada uma taxa de $2. No mês passado, ele usou o caixa eletrônico oito vezes. Quanto foi a taxa total dele pelo uso do caixa eletrônico?
- Responda
-
Uma taxa de $16 foi deduzida de sua conta corrente.
Conceitos chave
- Multiplicação e divisão de dois números assinados
- Mesmos sinais: o produto é positivo
- Sinais diferentes — o produto é negativo
- Estratégia para aplicativos
- Identifique o que você deve encontrar.
- Escreva uma frase que forneça as informações para encontrá-la.
- Traduza a frase para uma expressão.
- Simplifique a expressão.
- Responda à pergunta com uma frase completa.


