1.4: Adicionar e subtrair números inteiros
- Page ID
- 184482
- Use negativos e opostos
- Simplifique: expressões com valor absoluto
- Adicionar números inteiros
- Subtraia números inteiros
Uma introdução mais completa aos tópicos abordados nesta seção pode ser encontrada no capítulo Pré-álgebra, Inteiros.
Use negativos e opostos
Nosso trabalho até agora incluiu apenas os números de contagem e os números inteiros. Mas se você já experimentou uma temperatura abaixo de zero ou sacou acidentalmente sua conta corrente, você já está familiarizado com números negativos. Números negativos são números menores que\(0\). Os números negativos estão à esquerda de zero na reta numérica. Veja a Figura\(\PageIndex{1}\).
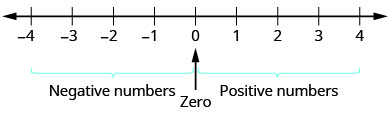
As setas nas extremidades da linha numérica indicam que os números continuam para sempre. Não há maior número positivo e não há menor número negativo.
Zero é um número positivo ou negativo? Números maiores que zero são positivos e números menores que zero são negativos. Zero não é positivo nem negativo.
Considere como os números são ordenados na reta numérica. Indo da esquerda para a direita, os números aumentam de valor. Indo da direita para a esquerda, os números diminuem em valor. Veja a Figura\(\PageIndex{2}\).
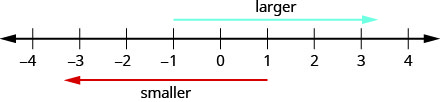
Fazer a atividade de matemática manipulativa “Linha numérica - parte 2” ajudará você a desenvolver uma melhor compreensão dos números inteiros.
Lembre-se de que usamos a notação:
\(a \lt b\)(leia “\(a\)é menor que\(b\)”) quando\(a\) está à\(b\) esquerda da reta numérica.
\(a \gt b\)(leia “\(a\)é maior que\(b\)”) quando\(a\) está à\(b\) direita da reta numérica.
Agora precisamos estender a reta numérica que mostrava os números inteiros para incluir também números negativos. Os números marcados por pontos na Figura\(\PageIndex{3}\). são chamados de números inteiros. Os números inteiros são os números\(...−3, −2, −1, 0, 1, 2, 3…\)
Ordene cada um dos seguintes pares de números usando\(<\) ou\(>\):
- \(14 \; \_\_\_\; 6\)
- \(-1\; \_\_\_ \;9\)
- \(-1\; \_\_\_ -4\)
- \(\;\; 2 \;\_\_\_ -20\)
Solução:
Pode ser útil consultar a linha numérica mostrada.
Figura\(\PageIndex{4}\)
\ (\ begin {align*} 1. \ quad & 14\;\ _\ _\ _\; 6\\ [4pt]
& 14 > 6 &&\ text {\(14\)está à\(6\) direita da reta numérica.}\\ [8pt]
2. \ quad & -1\;\ _\ _\ _\; 9\\ [4pt]
& -1 < 9 &&\ text {\(-1\)está à\(9\) esquerda da reta numérica.}\\ [8pt]
3. \ quad & -1\;\ _\ _\ _-4\\ [4pt]
& -1 > -4 &&\ text {\(-1\)está à\(-4\) direita da reta numérica.}\\ [8pt]
4. \ quad & 2\;\ _\ _\ _-20\\ [4pt]
& 2 > -20 &&\ text {\(2\)está à\(-20\) direita da reta numérica.} \
\ end {align*}\)
Experimente\(\PageIndex{1}\)
Ordene cada um dos seguintes pares de números, usando\(<\) or \(>\):
- \(15 \; \_\_\_\; 7\)
- \(-2 \; \_\_\_\; 5\)
- \(-3 \; \_\_\_\; -7\)
- \(5 \; \_\_\_\; -17\)
- Answer
-
- \(<\)
- \(>\)
- \(<\)
- \(>\)
Try It \(\PageIndex{2}\)
Ordene cada um dos seguintes pares de números usando\(<\) ou\(>\):
- \(8 \; \_\_\_\; 13\)
- \(3 \; \_\_\_\; -4\)
- \(-5 \; \_\_\_\; -2\)
- \(9 \; \_\_\_\; -21\)
- Responda
-
- \(<\)
- \(>\)
- \(<\)
- \(>\)
Você deve ter notado que, na reta numérica, os números negativos são uma imagem espelhada dos números positivos, com zero no meio. Como os números\(2\)\(−2\) estão à mesma distância de zero, eles são chamados de s opostos. O oposto de\(2\) é\(−2\) e o oposto de\(−2\) é\(2\).
O oposto de um número é o número que está à mesma distância de zero na reta numérica, mas no lado oposto de zero.
A figura\(\PageIndex{5}\) ilustra a definição.
Às vezes, em álgebra, o mesmo símbolo tem significados diferentes. Assim como algumas palavras em inglês, o significado específico fica claro ao observar como ele é usado. Você viu o símbolo “\(−\)” usado de três maneiras diferentes.
\ [\ begin {align*} &10 − 4\ quad\ text {Entre dois números, indica a operação de}\ textit {subtração}.\\ &\ qquad\ qquad\ text {Lemos} 10 - 4\,\ text {como “} 10\,\ text {minus}\, 4. \ text {”}\\ [5pt]
&-8\ quad\ text {Na frente de um número, indica um}\ textit {negativo}\ text {número.}\\ &\ qquad\ qquad\ text {Lemos} -8\ text {como “menos oito”.}\\ [5pt]
&-x\ quad\ text {Na frente de uma variável, indica o}\ textit {oposto.}\\ &\ qquad\ qquad\ text {Lemos} -x\ text {como “o oposto de} x\ text {”}\\ [5pt]
&- (-2)\ quad\ text {Aqui há dois sinais “−”.} \\
&\ qquad\ qquad\ text {O que está entre parênteses nos diz que o número é negativo} 2. \\
&\ qquad\ qquad\ text {Aquele fora dos parênteses nos diz para pegar o}\ textit {oposto}\ text {of} −2. \\
&\ qquad\ qquad\ text {Lemos} − (−2)\ text {como “o oposto de menos dois”.} \ end {align*}\]
\(−a\)significa o oposto do número\(a\).
A notação\(−a\) é lida como “o oposto de”\(a\).
Encontre:
- o oposto de\(7\)
- o oposto de\(−10\)
- o oposto de\(−(−6)\)
Solução:
1. \( \quad −7\)está à\(0\) mesma distância de\(7\), mas no lado oposto de\(0\). O oposto de\(7\) nós\(-7\).
2. \( \quad 10\)está à\(0\) mesma distância de\(−10\), mas no lado oposto de\(0\). O oposto de\(-10\) nós\(10\).
3. \(\quad\)O oposto de\(-(-6)\) nós\(-6\).
Experimente\(\PageIndex{3}\)
Encontre:
- o oposto de\(4\)
- the opposite of \(−3\)
- \(−(−1)\)
- Answer
-
- \(-4\)
- \(3\)
- \(1\)
Try It \(\PageIndex{4}\)
Encontre:
- o oposto de\(8\)
- o oposto de\(−5\)
- \(−(−5)\)
- Responda
-
- \(-8\)
- \(5\)
- \(5\)
Nosso trabalho com opostos nos dá uma maneira de definir os números inteiros. Os números inteiros e seus opostos são chamados de números inteiros. Os números inteiros são os números\(…−3,−2,−1,0,1,2,3…\)
Os números inteiros e seus opostos são chamados de números inteiros.
Os números inteiros são os números
\[…−3,−2,−1,0,1,2,3… \nonumber \]
Ao avaliar o oposto de uma variável, devemos ter muito cuidado. Sem saber se a variável representa um número positivo ou negativo, não sabemos se −x−x é positivo ou negativo. Podemos ver isso em Example\(\PageIndex{1}\).
Avalie
- \(-x\), quando\(x = 8\)
- \(-x\), quando\(x = -8\)
Solução:
-
-x 
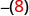
Escreva o oposto de 8. -8 -
-x 
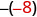
Escreva o oposto de -8. 8
Experimente\(\PageIndex{5}\)
Avalie\(-n\), when
- \(n = 4\)
- \(n = -4\)
- Answer
-
- \(-4\)
- \(4\)
Try It \(\PageIndex{6}\)
Avalie\(-m\), quando
- \(m = 11\)
- \(m = -11\)
- Responda
-
- \(-11\)
- \(11\)
Simplifique: expressões com valor absoluto
Vimos que números como\(2\) e\(−2\) são opostos porque estão à mesma distância da\(0\) reta numérica. Ambos estão a duas unidades de\(0\). A distância entre\(0\) e qualquer número na reta numérica é chamada de valor absoluto desse número.
O valor absoluto de um número é sua distância da\(0\) reta numérica.
O valor absoluto de um número\(n\) é escrito como\(|n|\).
Por exemplo,
- \(−5\)está a\(5\) unidades de distância\(0\), então\(|−5|=5\).
- \(5\)está a\(5\) unidades de distância\(0\), então\(|5|=5\).
A figura\(\PageIndex{6}\) ilustra essa ideia.
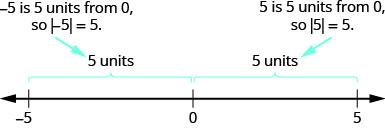
O valor absoluto de um número nunca é negativo (porque a distância não pode ser negativa). O único número com valor absoluto igual a zero é o próprio número zero, porque a distância de\(0\) até\(0\) na reta numérica é zero unidades.
\(|n| \geq 0\)para todos os números
Os valores absolutos são sempre maiores ou iguais a zero!
Os matemáticos dizem com mais precisão: “os valores absolutos são sempre não negativos”. Não negativo significa maior ou igual a zero.
Simplifique:
- \(|3|\)
- \(|-44|\)
- \(|0|\)
Solução:
O valor absoluto de um número é a distância entre o número e zero. A distância nunca é negativa, então o valor absoluto nunca é negativo.
- \( |3| = 3\)
- \(|-44| = 44\)
- \( |0| = 0\)
Experimente\(\PageIndex{7}\)
Simplifique:
- \(|4|\)
- \(|-28|\)
- \(|0|\)
- Answer
-
- \(4\)
- \(28\)
- \(0\)
Try It \(\PageIndex{8}\)
Simplifique:
- \(|-13|\)
- \(|47|\)
- Responda
-
- \(13\)
- \(47\)
No próximo exemplo, vamos ordenar expressões com valores absolutos. Lembre-se de que números positivos são sempre maiores do que números negativos!
\(<, >, \text{or} =\)Preencha cada um dos seguintes pares de números:
- \(|−5| \; {\underline{\hspace {2 em}}} \;−|−5|\)
- \(8 \;{\underline{\hspace {2 em}}} \;−|−8|\)
- \(-9 \;{\underline{\hspace {2 em}}} \;−|−9|\)
- \(-(-16) \;{\underline{\hspace {2 em}}}\; −|−16|\)
Solução:
\(\begin{array} {llll} {\text{Simplification}} &{|-5|} & {\underline{\hspace {2 em}}} &{-|-5|} \\ {\text{Order.}} &{5} &{\underline{\hspace {2 em}}} &{-5} \\ {} &{5} &{>} &{-5} \\ {} &{|-5|} &{>} &{-|-5|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{8} & {\underline{\hspace {2 em}}} &{-|-8|} \\ {\text{Order.}} &{8} &{\underline{\hspace {2 em}}} &{-8} \\ {} &{8} &{>} &{-8} \\ \text{so }\\ {} & {|8|} &{>} &{-|-8|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{-9} & {\underline{\hspace {2 em}}} &{-|-9|} \\ {\text{Order.}} &{-9} &{\underline{\hspace {2 em}}} &{-9} \\ {} &{-9} &{=} &{-9} \\ \text{so } \\ {} & {-9} &{=} &{-|-9|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{-(-16)} & {\underline{\hspace {2 em}}} &{-|16|} \\ {\text{Order.}} &{16} &{\underline{\hspace {2 em}}} &{-16} \\ {} &{16} &{>} &{-16} \\ \text{so } \\ {} & {-(-16)} &{>} &{-|-16|} \\ \end{array}\)
Experimente\(\PageIndex{9}\)
Preencha\(<, >, \text{or} =\) for each of the following pairs of numbers:
- \(|−9| \;{\underline{\hspace {2 em}}} \; −|−9|\)
- \(2 \;{\underline{\hspace {2 em}}} \; −|−2|\)
- \(-8 \;{\underline{\hspace {2 em}}} \; −|−8|\)
- \(-(-9) \;{\underline{\hspace {2 em}}} \; −|−9|\)
- Answer
-
- \(>\)
- \(>\)
- \(<\)
- \(>\)
Try It \(\PageIndex{10}\)
\(<, >, \text{or} =\)Preencha cada um dos seguintes pares de números:
- \(7 \;{\underline{\hspace {2 em}}} \; −|−7|\)
- \(-(-10) \;{\underline{\hspace {2 em}}} \; −|−10|\)
- \(|-4| \;{\underline{\hspace {2 em}}} \; −|−4|\)
- \(-1 \;{\underline{\hspace {2 em}}} \; |−1|\)
- Responda
-
- \(>\)
- \(>\)
- \(>\)
- \(<\)
Agora adicionamos barras de valor absoluto à nossa lista de símbolos de agrupamento. Quando usamos a ordem das operações, primeiro simplificamos o máximo possível dentro das barras de valor absoluto e, em seguida, tomamos o valor absoluto do número resultante.
\[\begin{array} {llll} {\text{Parentheses}} &{()} & {\text{Braces}} & {\{\}} \\ {\text{Brackets}} &{[\space]} &{\text{Absolute}} &{|\space|} \\ \end{array} \nonumber\]
No próximo exemplo, simplificaremos primeiro as expressões dentro das barras de valor absoluto, assim como fazemos com parênteses.
Simplifique:\(24 - |19 - 3(6 - 2)|\)
Solução:
\[\begin{array} {ll} {} &{24 - |19 - 3(6 - 2)|} \\ {\text{Work inside parentheses first: subtract } 2\space \text{from } 6} &{24 - |19 - 3(4)|} \\ {\text{Multiply }3(4)} &{24 - |19 - 12|} \\ {\text{Subtract inside the absolute value bars. }} &{24 - |7|} \\ {\text{Take the absolute value.}} &{24 - 7} \\ {\text{Subtract.}} &{17} \end{array}\nonumber\]
Experimente\(\PageIndex{11}\)
Simplifique:\(19 - |11 - 4(3 - 1)|\)
- Answer
-
\(16\)
Try It \(\PageIndex{12}\)
Simplifique:\(9 - |8 - 4(7 - 5)|\)
- Responda
-
\(9\)
Avalie:
- \(|x|\)quando\(x = -35\)
- \(|y|\)quando\(y = -20\)
- \(-|u|\)quando\(u = 12\)
- \(-|p|\)quando\(p = -14\)
Solução:
1. \(|x|\)quando\(x = -35\)
\(\begin{array} {ll} {} &{|x|} \\ {\text{Substitute } -35 \space \text{for }x} &{|-35|} \\ {\text{Take the absolute value.}} &{35} \end{array}\)
2. \(|y|\)quando\(y = -20\)
\(\begin{array} {ll} {} &{|-y|} \\ {\text{Substitute } -20 \space \text{for }y} &{|-(-20)|} \\ {\text{Simplify}} &{|20|} \\ {\text{Take the absolute value.}} &{20} \end{array}\)
3. \(-|u|\)quando\(u = 12\)
\(\begin{array} {ll} {} &{-|u|} \\ {\text{Substitute } 12 \space \text{for }u} &{|-12|} \\ {\text{Take the absolute value.}} &{-12} \end{array}\)
4. \(-|p|\)quando\(p = -14\)
\(\begin{array} {ll} {} &{-|p|} \\ {\text{Substitute } -14 \space \text{for }p} &{-|-14|} \\ {\text{Take the absolute value.}} &{-14} \end{array}\)
Experimente\(\PageIndex{13}\)
Avalie:
- \(|x|\) when \(x = -17\)
- \(|y|\) when \(y = -39\)
- \(-|m|\) when \(m = 22\)
- \(-|p|\) when \(p = -11\)
- Answer
-
- \(17\)
- \(39\)
- \(-22\)
- \(-11\)
Try It \(\PageIndex{14}\)
Avalie:
- \(|y|\)quando\(y = -23\)
- \(|-y|\)quando\(y = -21\)
- \(-|n|\)quando\(n = 37\)
- \(-|q|\)quando\(q = -49\)
- Responda
-
- \(23\)
- \(21\)
- \(-37\)
- \(-49\)
Adicionar números inteiros
A maioria dos estudantes se sente confortável com os fatos de adição e subtração para números positivos. Mas fazer adição ou subtração com números positivos e negativos pode ser mais desafiador.
Fazer a atividade de matemática manipulativa “Adição de números assinados” ajudará você a desenvolver uma melhor compreensão da adição de números inteiros.”
Usaremos dois contadores de cores para modelar a adição e a subtração de negativos para que você possa visualizar os procedimentos em vez de memorizar as regras.
Deixamos que uma cor (azul) represente o positivo. A outra cor (vermelha) representará os negativos. Se tivermos um contador positivo e um contador negativo, o valor do par será zero. Eles formam um par neutro. O valor desse par neutro é zero.
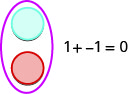
Usaremos os contadores para mostrar como adicionar os quatro fatos de adição usando os números\(5, −5\)\(3,−3\) e.
\[\begin{array} {llll} {5 + 3} &{-5 + (-3)} &{-5 + 3} &{5 + (-3)} \end{array} \nonumber \]
Para adicionar\(5+3\), percebemos que isso\(5+3\) significa a soma de\(5\)\(3\) e.
| Começamos com\(5\) pontos positivos. |  |
| E então adicionamos\(3\) pontos positivos. |  |
| Agora temos\(8\) pontos positivos. A soma de\(5\) e\(3\) é\(8\). |  |
Agora vamos adicionar\(−5 + (−3)\). Observe as semelhanças com o último exemplo\(5 + 3 = 8\).
Para adicionar\(−5 + (−3)\), percebemos que isso significa a soma de\(−5\)\(−3\) e.
| Começamos com\(5\) negativos. |  |
| E então adicionamos\(3\) negativos. |  |
| Agora temos o\(8\) negativo. A soma de\(-5\) e\(-3\) é\(-8\). |  |
De que forma esses dois primeiros exemplos foram semelhantes?
- O primeiro exemplo adiciona\(5\) pontos\(3\) positivos e positivos — ambos positivos.
- O segundo exemplo adiciona\(5\)\(3\) negativos e negativos — ambos negativos.
Em cada caso, obtivemos\(8\) —\(8\) positivos ou\(8\) negativos.
Quando os sinais eram os mesmos, os contadores eram todos da mesma cor, então os adicionamos.
Adicionar:
- \(1 + 4\)
- \(-1 + (-4)\)
Solução:
1. 
\(1\)positivo mais\(4\) positivo é\(5\) positivo.
2. 
\(1\)negativo mais\(4\) negativo é\(5\) negativo.
Experimente\(\PageIndex{15}\)
Adicionar:
- \(2 + 4\)
- \(-2 + (-4)\)
- Answer
-
- \(6\)
- \(-6\)
Try It \(\PageIndex{16}\)
Adicionar:
- \(2 + 5\)
- \(-2 + (-5)\)
- Responda
-
- \(7\)
- \(-7\)
Então, o que acontece quando os sinais são diferentes? Vamos adicionar\(−5+3\). Percebemos que isso significa a soma de\(−5\)\(3\) e. Quando os contadores eram da mesma cor, nós os colocamos em uma fileira. Quando os contadores são de uma cor diferente, nós os alinhamos um embaixo do outro.
| \(-5 + 3\)significa a soma de\(-5\)\(3\) e. | |
| Começamos com\(5\) negativos. |  |
| E então adicionamos\(3\) pontos positivos. |  |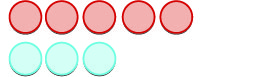
| Removemos todos os pares neutros. |  |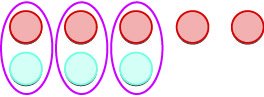
| Ainda temos\(2\) negativos. |  |
| A soma de\(-5\) e\(3\) é\(-2\). | \(-5 + 3 = 2\) |
Observe que houve mais negativos do que positivos, então o resultado foi negativo.
Vamos agora adicionar a última combinação,\(5+(−3)\).
| \(5 + (-3)\)significa a soma de\(-5\)\(-3\) e. | |
| Começamos com\(5\) pontos positivos. |  |
| E então adicionamos\(3\) negativos. |  |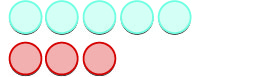
| Removemos todos os pares neutros. |  |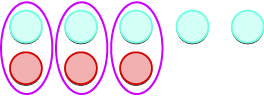
| Ainda temos\(2\) pontos positivos. |  |
| A soma de\(5\) e\(-3\) é\(2\). | \(5 + (-3) = 2\) |
Quando usamos contadores para modelar a adição de números inteiros positivos e negativos, é fácil ver se há mais contadores positivos ou mais negativos. Então, sabemos se a soma será positiva ou negativa.
Adicionar:
- \(-1 + 5\)
- \(1 + (-5)\)
Solução:
1. \(-1 + 5\)
Há mais pontos positivos, então a soma é positiva.
Então,\(-1 + 5 = 4\).
2. \(1 + (-5)\)
Há mais negativos, então a soma é negativa.
Então,\(1 + (-5) = -4\)
Experimente\(\PageIndex{17}\)
Adicionar:
- \(-2 + 4\)
- \(2 + (-4)\)
- Answer
-
- \(2\)
- \(-2\)
Try It \(\PageIndex{18}\)
Adicionar:
- \(-2 + 5\)
- \(2 + (-5)\)
- Responda
-
- \(3\)
- \(-3\)
Agora que adicionamos pequenos números inteiros positivos e negativos com um modelo, podemos visualizar o modelo em nossas mentes para simplificar problemas com qualquer número.
Quando você precisa adicionar números como\(37+(−53)\), você realmente não quer ter que contar contadores\(37\) azuis e contadores\(53\) vermelhos. Com o modelo em mente, você consegue visualizar o que faria para resolver o problema?
Imagine balcões\(37\) azuis com contadores\(53\) vermelhos alinhados embaixo. Como haveria mais contadores vermelhos (negativos) do que azuis (positivos), a soma seria negativa. Quantos contadores vermelhos mais existiriam? Porque\(53−37=16\) há\(16\) mais contadores vermelhos.
Portanto, a soma de\(37+(−53)\) é\(−16\).
\[37+(−53)=−16\nonumber\]
Vamos tentar outro. Vamos adicionar\(−74+(−27)\). Novamente, imagine\(74\) contadores vermelhos e\(27\) mais contadores vermelhos, então teríamos contadores\(101\) vermelhos. Isso significa que a soma é\(−101\).
\[−74+(−27)=−101\nonumber\]
Vamos analisar novamente os resultados da adição das diferentes combinações de\(5,−5\)\(3, -3\) e.
\[\begin{array} {ll} {5 + 3=8} &{-5 + (-3)=-8} \\{\text{both positive, sum positive}} &{\text{both positive, sum positive}} \end{array}\nonumber\]
Quando os sinais são iguais, os contadores seriam todos da mesma cor, então adicione-os.
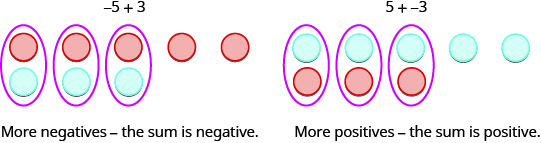
\[\begin{array} {ll} {5 + 3=-2} &{-5 + (-3)=2} \\{\text{different signs, more negatives, sum negative}} &{\text{different signs, more positives, sum positive}} \end{array}\nonumber\]
Quando os sinais são diferentes, alguns dos contadores formariam pares neutros, então subtraia para ver quantos restam.
Visualize o modelo ao simplificar as expressões nos exemplos a seguir.
Simplifique:
- \(19 + (-47)\)
- \(-14 + (-36)\)
Solução:
1. Como os sinais são diferentes, subtraímos\(19\) de\(47\). A resposta será negativa porque há mais pontos negativos do que positivos.
\(\text{Add.} \qquad 19 + (-47) = -28\)
2. Como os sinais são os mesmos, adicionamos. A resposta será negativa porque há mais pontos negativos do que positivos.
\(\text{Add.} \qquad-14 + (-36) = -50\)
Experimente\(\PageIndex{19}\)
Simplifique:
- \(-31 + (-19)\)
- \(15 + (-32)\)
- Answer
-
- \(-50\)
- \(-17\)
Try It \(\PageIndex{20}\)
Simplifique:
- \(-42 + (-28)\)
- \(25 + (-61)\)
- Responda
-
- \(-70\)
- \(-36\)
As técnicas usadas até agora se estendem a problemas mais complicados, como os que vimos antes. Lembre-se de seguir a ordem das operações!
Simplifique:
\(-5 + 3(-2 + 7)\)
Solução:
\[\begin{array} {ll} {} &{-5 + 3(-2 + 7)} \\ {\text{Simplify inside the parenthesis}} &{-5 + 3(5)} \\{\text{Multiply}} &{-5 + 15} \\{\text{add left to right}} &{10} \end{array}\nonumber\]
Experimente\(\PageIndex{21}\)
Simplifique:
\(-2 + 5(-4 + 7)\)
- Answer
-
\(13\)
Try It \(\PageIndex{22}\)
Simplifique:
\(-4 + 2(-3 + 5)\)
- Responda
-
\(0\)
Subtraia números inteiros
Fazer a atividade de matemática manipulativa “Subtração de números assinados” ajudará você a desenvolver uma melhor compreensão da subtração de números inteiros.
Continuaremos a usar contadores para modelar a subtração. Lembre-se de que os contadores azuis representam números positivos e os contadores vermelhos representam números negativos.
Talvez quando você era mais jovem, você lesse “\(5−3\)” como “\(5\)levar embora”\(3\). Quando você usa contadores, você pode pensar em subtração da mesma maneira!
Vamos modelar os quatro fatos de subtração usando os números\(5\)\(3\) e.
\[\begin{array} {llll} {5 - 3} &{-5 - (-3))} &{-5 -3} &{5 - (-3)} \end{array}\nonumber\]
Para subtrair\(5−3\), reafirmamos o problema como “\(5\)retirar”\(3\).
| Começamos com\(5\) pontos positivos. |  |
| Nós “tiramos” os\(3\) pontos positivos. |  |
| Ainda temos\(2\) pontos positivos. | |
| A diferença de\(5\) e\(3\) é\(2\). | \(2\) |
Agora vamos subtrair\(−5−(−3)\). Observe as semelhanças com o último exemplo\(5−3=2\).
Para subtrair\(−5−(−3)\), reafirmamos isso como “\(–5\)retirar\(–3\)”
| Começamos com\(5\) negativos. |  |
|
Nós “eliminamos”\(3\) os negativos. |
 |
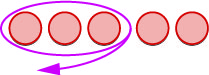| Ainda temos\(2\) negativos. | |
| A diferença de\(-5\) e\(-3\) é\(-2\). |
\(-2\) |
Observe que esses dois exemplos são muito parecidos: no primeiro exemplo, subtraímos 3 positivos de 5 positivos e terminamos com 2 positivos.
No segundo exemplo, subtraímos 3 negativos de 5 negativos e terminamos com 2 negativos.
Cada exemplo usava contadores de apenas uma cor, e o modelo de subtração “take away” era fácil de aplicar.
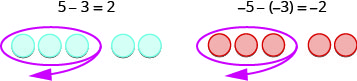
Subtrair:
- \(7 - 5\)
- \(-7 - (-5)\)
Solução:
- \[\begin{array} {ll} {7 - 5} \\ {2}&{\text{Take }5\space \text{positives from }7 \space \text{positives and get }2\space \text{positives}} & \end{array}\nonumber\]
- \[\begin{array} {ll} {-7 - (-5)} \\ {-2} &{\text{Take }5\space \text{negatives from }7 \space \text{negatives and get }2\space \text{negatives}} \end{array}\nonumber\]
Experimente\(\PageIndex{23}\)
Subtrair:
- \(6 - 4\)
- \(-6 - (-4)\)
- Answer
-
- \(2\)
- \(-2\)
Try It \(\PageIndex{24}\)
Subtrair:
- \(7 - 4\)
- \(-7 - (-4)\)
- Responda
-
- \(3\)
- \(-3\)
O que acontece quando temos que subtrair um número positivo e um negativo? Precisaremos usar contadores brancos e vermelhos, bem como alguns pares neutros. Adicionar um par neutro não altera o valor. É como trocar quartos por níquel — o valor é o mesmo, mas parece diferente.
- Para subtrair\(−5−3\), reafirmamos isso como “\(−5\)take away\(3\)”.
Começamos com\(5\) negativos. Precisamos retirar os\(3\) pontos positivos, mas não temos nenhum positivo para tirar.
Lembre-se de que um par neutro tem valor zero. Se adicionarmos\(0\) ao\(5\) seu valor, ainda é\(5\). Adicionamos pares neutros aos\(5\) negativos até obtermos\(3\) pontos positivos a serem eliminados.
| \(-5 -3\)significa\(-5\) levar embora\(3\) | |
| Começamos com\(5\) negativos. |  |
| Agora adicionamos os neutros necessários para obter\(3\) pontos positivos. |  |
| Nós removemos os\(3\) pontos positivos. |  |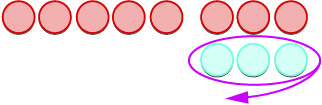
| Ficamos com\(8\) os negativos. |  |
| A diferença de\(-5\) e\(3\) é\(-8\). | \(-5 - 3 = -8\) |
E agora, o quarto caso,\(5−(−3)\). Começamos com\(5\) pontos positivos. Precisamos eliminar os\(3\) negativos, mas não há negativos a serem retirados. Então, adicionamos pares neutros até termos\(3\) negativos a serem eliminados.
| \(5 -(-3)\)significa\(5\) levar embora\(-3\) | |
| Começamos com\(5\) pontos positivos. |  |
| Agora adicionamos os pares de neutros necessários. |  |
| Nós removemos os\(3\) negativos. |  |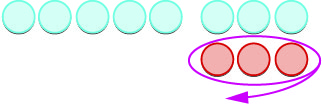
| Ficamos com\(8\) pontos positivos. |  |
| A diferença de\(5\) e\(-3\) é\(8\). | \(5 - (-3) = 8\) |
Subtrair:
- \(-3 -1\)
- \(3 - (-1)\)
Solução:
1.
|
Pegue 1 positivo do único par neutro adicionado. |
  |
\(\begin{array} {l} {-3 -1} \\ {-4} \end{array}\) |
|
Pegue 1 negativo do único par neutro adicionado. |
  |
\(\begin{array} {l} {3 - (-1)} \\ {4} \end{array}\) |
Experimente\(\PageIndex{25}\)
Subtrair:
- \(-6 -4\)
- \(6 - (-4)\)
- Answer
-
- \(-10\)
- \(10\)
Try It \(\PageIndex{26}\)
Subtrair:
- \(-7-4\)
- \(7 - (-4)\)
- Responda
-
- \(-11\)
- \(11\)
Você notou que a subtração de números assinados pode ser feita adicionando o oposto? No Exercício\(\PageIndex{33}\),\(−3−1\) é o mesmo\(−3+(−1)\) e\(3−(−1)\) é o mesmo que\(3+1\). Muitas vezes você verá essa ideia, a propriedade de subtração, escrita da seguinte forma:
\[a−b=a+(−b) \nonumber\]
Subtrair um número é o mesmo que somar seu oposto.
Veja esses dois exemplos.
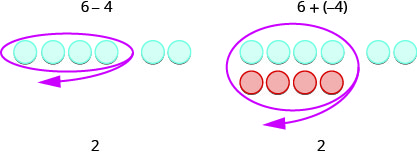
Claro, quando você tem um problema de subtração que tem apenas números positivos, por exemplo\(6−4\), você simplesmente faz a subtração. Você já sabia como subtrair há\(6−4\) muito tempo. Mas saber disso\(6−4\) dá a mesma resposta que\(6+(−4)\) ajuda quando você está subtraindo números negativos. Certifique-se de entender como\(6−4\) e de\(6+(−4)\) dar os mesmos resultados!
Simplifique:
- \(13 - 8 \space \text{and } 13 + (-8)\)
- \(-17 - 9 \space \text{and } -17 + (-9)\)
Solução:
- \(\begin{array} {llll} {\text{Subtract.}} &{13 - 8} &{\text{and}} &{13 + (-8)} \\ {} &{5} &{} &{5} \end{array}\)
- \(\begin{array} {llll} {\text{Subtract.}} &{-17 - 9} &{\text{and}} &{-17 + (-9)} \\ {} &{-26} &{} &{-26} \end{array}\)
Experimente\(\PageIndex{27}\)
Simplifique:
- \(21 - 13 \space \text{and } 21 + (-13)\)
- \(-11 - 7 \space \text{and } -11 + (-7)\)
- Answer
-
- \(8\)
- \(-18\)
Try It \(\PageIndex{28}\)
Simplifique:
- \(15 - 7 \space \text{and } 15 + (-7)\)
- \(-14 - 8 \space \text{and } -14 + (-8)\)
- Responda
-
- \(8\)
- \(-22\)
Veja o que acontece quando subtraímos um negativo.
Subtrair um número negativo é como adicionar um número positivo!
Muitas vezes você verá isso escrito como\(a−(−b)=a+b\).
Isso também funciona para outros números? Vamos fazer o exemplo a seguir e ver.
Simplifique:
- \(9 - (-15) \space \text{and } 9 + 15\)
- \(-7 - (-4) \space \text{and } -7 + 4\)
Solução:
- \(\begin{array} {lll} {} &{9 - (-15)} &{9 + 15} \\ {\text{Subtract}} &{24} &{24} \end{array}\)
- \(\begin{array} {lll} {} &{-7 - (-4)} &{-7 + 4} \\ {\text{Subtract}} &{-3} &{-3} \end{array}\)
Experimente\(\PageIndex{29}\)
Simplifique:
- \(6 - (-13) \space \text{and } 6 + 13\)
- \(-5 - (-1) \space \text{and } -5 + 1\)
- Answer
-
- \(19\)
- \(-4\)
Try It \(\PageIndex{30}\)
Simplifique:
- \(4 - (-19) \space \text{and } 4 + 19\)
- \(-4 - (-7) \space \text{and } -4 + 7\)
- Responda
-
- \(23\)
- \(3\)
Vamos analisar novamente os resultados da subtração das diferentes combinações de\(5,−5\)\(3,−3\) e.
\[\begin{array} {l} {5 - 3} &{-5 - (-3)} \\ {2} &{-2} \\ {5\space\text{positives take away }3\space\text{positives}} &{5\space\text{negatives take away }3\space\text{negatives}} \\ {2\space\text{positives}} &{2\space\text{negatives}} \end{array}\nonumber\]
Quando houver contadores suficientes da cor para remover, subtraia.
\[\begin{array} {l} {-5 - 3} &{5 - (-3)} \\ {-8} &{8} \\ {5\space\text{negatives, want to take away }3\space\text{positives}} &{5\space\text{positives, want to take away }3\space\text{negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}} \end{array}\nonumber\]
Quando não houvesse contadores suficientes da cor para retirar, adicione.
O que acontece quando há mais de três números inteiros? Nós apenas usamos a ordem das operações normalmente.
Simplifique:
\(7 - (-4 -3) - 9\)
Solução:
\[ \begin{array} {ll} {} &{7 - (-4 - 3) - 9} \\ {\text{Simplify inside the parenthesis first.}} &{7 - (-7) - 9} \\ {\text{Subtract left to right.}} &{14 - 9} \\ {\text{Subtract}} &{5} \end{array}\nonumber\]
Experimente\(\PageIndex{31}\)
Simplifique:
\(8−(−3−1)−9\)
- Answer
-
\(3\)
Try It \(\PageIndex{32}\)
Simplifique:
\(12−(−9−6)−14\)
- Responda
-
\(12\)
Acesse esses recursos on-line para obter instruções adicionais e praticar a adição e a subtração de números inteiros. Você precisará habilitar o Java em seu navegador para usar os aplicativos.
Conceitos-chave
- Adição de números inteiros positivos e negativos
\[\begin{array} {ll} {5 + 3} &{-5+(-3)} \\ {8} &{-8} \\ {\text{both positive,}} &{\text{both negative,}} \\ {\text{sum positive}} &{\text{sum negative}} \end{array}\nonumber\]
\[\begin{array} {ll} {-5 + 3} &{5+(-3)} \\ {-2} &{2} \\ {\text{different signs,}} &{\text{different signs,}} \\ {\text{more negatives}} &{\text{more positives}} \\ {\text{sum negative}} &{\text{sum positive}} \end{array}\nonumber\]
- Propriedade de valor absoluto:
\(|n| \geq 0\)para todos os números. Os valores absolutos são sempre maiores ou iguais a zero!
- Subtração de números inteiros
\[\begin{array} {ll} {5 - 3} &{-5-(-3)} \\ {2} &{-2} \\ {5\space\text{positives}} &{5\space\text{negatives}} \\ {\text{take away 3 positives}} &{\text{take away 3 negatives}} \\ {\text{2 positives}} &{\text{2 negatives}} \end{array}\nonumber\]
\[\begin{array} {ll} {-5 - 3} &{5-(-3)} \\ {-8} &{8} \\ {\text{5 negatives, want to}} &{\text{5 positives, want to}} \\ {\text{subtract 3 positives}} &{\text{subtract 3 negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}}\end{array}\nonumber\]
- Propriedade de subtração: subtrair um número é o mesmo que adicionar seu oposto.
Glossário
- valor absoluto
- O valor absoluto de um número é sua distância de 0 na reta numérica. O valor absoluto de um número nn é escrito como |n|.
- números inteiros
- Os números inteiros e seus opostos são chamados de números inteiros:\(...−3, −2, −1, 0, 1, 2, 3...\)
- oposto
- O oposto de um número é o número que está à mesma distância de zero na reta numérica, mas no lado oposto de zero: −\(a\) significa o oposto do número. A notação −\(a\) é lida como “o oposto de”\(a\).