Skip to main content
Global

1.2: Introdução aos números inteiros

  1. Last updated
  2. Save as PDF
  • Page ID
    184429

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de
    • Ao final desta seção, você poderá:
    • Use o valor posicional com números inteiros
    • Identifique múltiplos e aplique testes de divisibilidade
    • Encontre fatorizações primárias e múltiplos menos comuns

    Ao começarmos nosso estudo da álgebra elementar, precisamos atualizar algumas de nossas habilidades e vocabulário. Este capítulo se concentrará em números inteiros, inteiros, frações, decimais e números reais. Também começaremos nosso uso de notação algébrica e vocabulário.

    Use o valor posicional com números inteiros

    Os números mais básicos usados em álgebra são os números que usamos para contar objetos em nosso mundo:\(1, 2, 3, 4\), e assim por diante. Eles são chamados de números de contagem s. Os números de contagem também são chamados de números naturais. Se adicionarmos zero aos números de contagem, obteremos o conjunto de números inteiros s.

    • Contando números:\(1, 2, 3, …\)
    • Números inteiros:\(0, 1, 2, 3, …\)

    A notação “\(…\)” é chamada de elipse e significa “e assim por diante”, ou que o padrão continua indefinidamente.

    Podemos visualizar números de contagem e números inteiros em uma reta numérica (veja a Figura\(\PageIndex{1}\)).

    Uma linha numérica horizontal com setas em cada extremidade e valores de zero a seis corre ao longo da parte inferior do diagrama. Uma segunda linha horizontal com uma seta voltada para a esquerda fica acima da primeira e se estende de zero a três. Essa linha é rotulada como “menor”. Uma terceira linha horizontal com uma seta voltada para a direita fica acima das duas primeiras, mas vai de três a seis e é rotulada como “maior”.
    Figura\(\PageIndex{1}\): Os números na reta numérica ficam maiores à medida que vão da esquerda para a direita e menores à medida que vão da direita para a esquerda. Embora essa linha numérica mostre apenas os números\(0\) inteiros\(6\), os números continuam sem fim.

    Fazer a atividade de Matemática Manipulativa “Linha Numérica - Parte 1” ajudará você a desenvolver uma melhor compreensão da contagem de números e dos números inteiros.

    Nosso sistema numérico é chamado de sistema de valor posicional, porque o valor de um dígito depende de sua posição em um número. A figura\(\PageIndex{2}\) mostra os valores posicionais. Os valores posicionais são separados em grupos de três, chamados de períodos. Os períodos são um, milhares, milhões, bilhões, trilhões e assim por diante. Em um número escrito, as vírgulas separam os pontos.

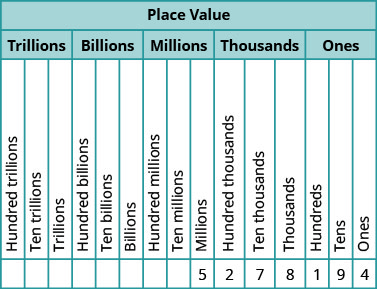
    Esta figura é uma tabela que ilustra o número 5.278.194 dentro do sistema de valor posicional. A tabela é mostrada com uma linha de cabeçalho, chamada “Valor posicional”, dividida em uma segunda linha de cabeçalho chamada “Trilhões”, “Bilhões”, “Milhões”, “Milhares” e “Unidades”. Sob o cabeçalho “Trilhões”, há três colunas rotuladas, escritas de baixo para cima, que dizem “Cem trilhões”, “Dez trilhões” e “Trilhões”. Sob o cabeçalho “Bilhões”, há três colunas rotuladas, escritas de baixo para cima, que dizem “Cem bilhões”, “Dez bilhões” e “Bilhões”. Sob o cabeçalho “Milhões”, há três colunas rotuladas, escritas de baixo para cima, que dizem “Cem milhões”, “Dez milhões” e “Milhões”. Sob o cabeçalho “Milhares”, há três colunas rotuladas, escritas de baixo para cima, que dizem “Cem milhares”, “Dez milhares” e “Milhares”. Sob o cabeçalho “Unidades”, há três colunas rotuladas, escritas de baixo para cima, que dizem “Centenas”, “Dezenas” e “Unidades”. Da esquerda para a direita, abaixo das colunas denominadas “Milhões”, “Cem milhares”, “Dez milhares”, “Milhares”, “Centenas”, “Dezenas” e “Unidades”, estão os seguintes valores: 5, 2, 7, 8, 1, 9, 4. Isso significa que existem 5 milhões, duzentos milhares, 7 dez milhares, 8 milhares, cem, 9 dezenas e 4 unidades no número cinco milhões duzentos e setenta e nove mil cento e noventa e quatro.
    Figura\(\PageIndex{2}\): O número\(5278194\) é mostrado no gráfico. O dígito\(5\) está na casa dos milhões. O dígito\(2\) está na casa das centenas de milhares. O dígito\(7\) está na casa dos dez milhares. O dígito\(8\) está na casa dos milhares. O dígito\(1\) está na casa das centenas. O dígito\(9\) está na casa das dezenas. O dígito\(4\) está no lugar das unidades.
    Exercício\(\PageIndex{1}\)

    No número\(63407218\), encontre o valor posicional de cada dígito:

    1. \(7\)
    2. \(0\)
    3. \(1\)
    4. \(6\)
    5. \(3\)
    Resposta

    Coloque o número na tabela de valores posicionais:

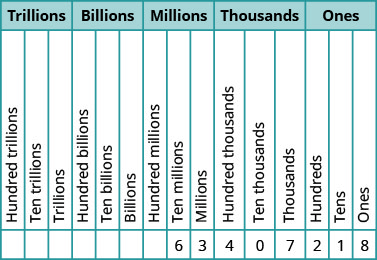
    Esta figura é uma tabela que ilustra o número 63.407.218 dentro do sistema de valor posicional. A tabela é mostrada com uma linha de cabeçalho, chamada “Valor posicional”, dividida em uma segunda linha de cabeçalho chamada “Trilhões”, “Bilhões”, “Milhões”, “Milhares” e “Unidades”. Sob o cabeçalho “Trilhões”, há três colunas rotuladas, escritas de baixo para cima, que dizem “Cem trilhões”, “Dez trilhões” e “Trilhões”. Sob o cabeçalho “Bilhões”, há três colunas rotuladas, escritas de baixo para cima, que dizem “Cem bilhões”, “Dez bilhões” e “Bilhões”. Sob o cabeçalho “Milhões”, há três colunas rotuladas, escritas de baixo para cima, que dizem “Cem milhões”, “Dez milhões” e “Milhões”. Sob o cabeçalho “Milhares”, há três colunas rotuladas, escritas de baixo para cima, que dizem “Cem milhares”, “Dez milhares” e “Milhares”. Sob o cabeçalho “Unidades”, há três colunas rotuladas, escritas de baixo para cima, que dizem “Centenas”, “Dezenas” e “Unidades”. Da esquerda para a direita, abaixo das colunas rotuladas “Dez milhões”, “Milhões”, “Cem milhares”, “Dez milhares”, “Milhares”, “Centenas”, “Dezenas” e “Unidades”, estão os seguintes valores: 6, 3, 4, 0, 7, 2, 1, 8. Isso significa que existem 6 dez milhões, 3 milhões, quatrocentos milhares, 0 dez milhares, 7 milhares, 2 centenas, 1 dez e 8 unidades no número sessenta e três milhões, quatrocentos e sete mil, duzentos e dezoito.
    1. O\(7\) está na casa dos milhares.
    2. O\(0\) está no lugar dos dez mil.
    3. O\(1\) está no lugar das dezenas.
    4. O\(6\) está na casa dos dez milhões.
    5. O\(3\) está na casa dos milhões.
    Exercício\(\PageIndex{2}\)

    Para o número\(27493615\), encontre o valor posicional de cada dígito:

    1. 2
    2. 1
    3. 4
    4. 7
    5. 5
    Resposta
    1. dez milhões
    2. dez
    3. cem milhares
    4. milhões
    5. uns
    Exercício\(\PageIndex{3}\)

    Para o número\(519711641328\), encontre o valor posicional de cada dígito:

    1. 9
    2. 4
    3. 2
    4. 6
    5. 7
    Resposta
    1. bilhões
    2. dez milhares
    3. dez
    4. cem milhares
    5. cem milhões

    Ao preencher um cheque, você escreve o número em palavras e também em dígitos. Para escrever um número em palavras, escreva o número em cada período, seguido pelo nome do período, sem o s no final. Comece pela esquerda, onde os períodos têm o maior valor. O período único não tem nome. As vírgulas separam os pontos, então, sempre que houver uma vírgula no número, coloque uma vírgula entre as palavras (veja a Figura\(\PageIndex{3}\)). O número\(74218369\) está escrito como setenta e quatro milhões, duzentos e dezoito mil, trezentos e sessenta e nove.

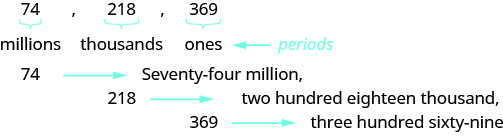
    Nesta figura, os números 74, 218 e 369 estão listados em uma linha, separados por vírgulas. Cada número tem um colchete abaixo dele com a palavra “milhões” escrita abaixo do número 74, “milhares” escrita abaixo do número 218 e “uns” escrita abaixo do número 369. Uma seta voltada para a esquerda aponta para essas três palavras, rotulando-as de “pontos”. Uma linha abaixo está o número “74”, uma seta para a direita e as palavras “Setenta e quatro milhões” seguidas por uma vírgula. A próxima linha abaixo é o número “218”, uma seta voltada para a direita e as palavras “duzentos e dezoito mil” seguidas por uma vírgula. Na linha inferior está o número “369”, uma seta voltada para a direita e as palavras “trezentos e sessenta e nove”.
    Figura\(\PageIndex{3}\)
    NOMEIE UM NÚMERO INTEIRO EM PALAVRAS.
    1. Comece à esquerda e nomeie o número em cada período, seguido pelo nome do período.
    2. Coloque vírgulas no número para separar os pontos.
    3. Não nomeie o ponto final.
    Exercício\(\PageIndex{4}\)

    Nomeie o número\(8165432098710\) usando palavras.

    Resposta

    Nomeie o número em cada período, seguido pelo nome do período.

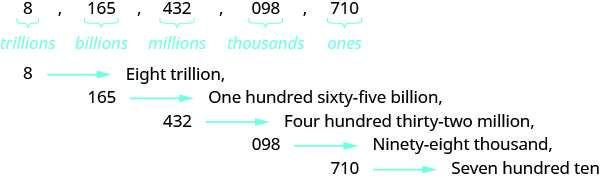
    Nesta figura, os números 8, 165, 432, 098 e 710 estão listados em uma linha, separados por vírgulas. Cada número tem um colchete horizontal abaixo com a palavra “trilhões” escrita abaixo do número 8, “bilhões” escrita abaixo do número 165, “milhões” escrita abaixo do número 432, “milhares” escrita abaixo do número 098 e “unidades” escrita abaixo do número 710. Uma linha abaixo está o número 8, uma seta voltada para a direita e as palavras “Oito trilhões” seguidas por uma vírgula. Na próxima linha abaixo está o número 165, uma seta voltada para a direita e as palavras “Cento e sessenta e cinco bilhões” seguidas por uma vírgula. Na próxima linha abaixo está o número 432, uma seta voltada para a direita e as palavras “Quatrocentos e trinta e dois milhões” seguidas por uma vírgula. Na próxima linha abaixo está o número “098”, uma seta voltada para a direita e as palavras “Noventa e oito mil” seguidas por uma vírgula. Na linha inferior está o número 710, uma seta voltada para a direita e as palavras “Setecentos e dez”.

    Coloque as vírgulas para separar os pontos.

    Então,\(8165432098710\) é nomeado como oito trilhões, cento e sessenta e cinco bilhões, quatrocentos e trinta e dois milhões, noventa e oito mil, setecentos e dez.

    Exercício\(\PageIndex{5}\)

    Nomeie o número 9.258.137.904.0619.258.137.904.061 usando palavras.

    Resposta

    nove trilhões, duzentos e cinquenta e oito bilhões, cento e trinta e sete milhões, novecentos e quatro mil, sessenta e um

    Exercício\(\PageIndex{6}\)

    Nomeie o número 17.864.325.619.00417.864.325.619.004 usando palavras.

    Resposta

    dezessete trilhões, oitocentos e sessenta e quatro bilhões, trezentos e vinte e cinco milhões, seiscentos e dezenove mil e quatro

    Agora vamos reverter o processo escrevendo os dígitos do nome do número. Para escrever o número em dígitos, primeiro procuramos as palavras-chave que indicam os pontos. É útil desenhar três espaços em branco para os períodos necessários e, em seguida, preenchê-los com os números, separando os períodos com vírgulas.

    ESCREVA UM NÚMERO INTEIRO USANDO DÍGITOS.
    1. Identifique as palavras que indicam períodos. (Lembre-se de que aquele período nunca tem nome.)
    2. Desenhe três espaços em branco para indicar o número de vagas necessárias em cada período. Separe os pontos por vírgulas.
    3. Nomeie o número em cada período e coloque os dígitos na posição correta do valor posicional.
    Exercício\(\PageIndex{7}\)

    Escreva nove bilhões, duzentos e quarenta e seis milhões, setenta e três mil, cento e oitenta e nove como um número inteiro usando dígitos.

    Resposta

    Identifique as palavras que indicam períodos.
    Com exceção do primeiro período, todos os outros períodos devem ter três vagas. Desenhe três espaços em branco para indicar o número de vagas necessárias em cada período. Separe os pontos por vírgulas.
    Em seguida, escreva os dígitos em cada período.

    Uma imagem tem duas linhas de texto. As linhas superiores dizem “nove bilhões”, seguido por uma vírgula, e “duzentos e quarenta e seis milhões”, também seguido por uma vírgula. As palavras “bilhão” e “milhão” estão sublinhadas e cada frase tem um colchete embaixo. As linhas inferiores dizem “setenta e três mil”, seguido por uma vírgula e “cento e oitenta e nove”. A palavra “mil” está sublinhada e cada frase tem um colchete embaixo.

    O número é 9.246.073.189.
    Exercício\(\PageIndex{8}\)

    Escreva o número dois bilhões, quatrocentos e sessenta e seis milhões, setecentos e quatorze mil, cinquenta e um como um número inteiro usando dígitos.

    Resposta

    2.466.714.051

    Exercício\(\PageIndex{9}\)

    Escreva o número onze bilhões, novecentos e vinte e um milhões, oitocentos e trinta mil, cento e seis como um número inteiro usando dígitos.

    Resposta

    11.921 830,106

    Em 2013, o Departamento de Censo dos EUA estimou a população do estado de Nova York em 19.651.127. Podemos dizer que a população de Nova York era de aproximadamente 20 milhões. Em muitos casos, você não precisa do valor exato; um número aproximado é bom o suficiente.

    O processo de aproximação de um número é chamado de arredondamento. Os números são arredondados para um valor posicional específico, dependendo da precisão necessária. Dizer que a população de Nova York é de aproximadamente 20 milhões significa que arredondamos para a casa dos milhões.

    Exercício\(\PageIndex{10}\) How to Round Whole Numbers

    Arredonde 23.658 para a centena mais próxima.

    Resposta

    Essa figura é uma tabela que tem três colunas e quatro linhas. A primeira coluna é uma coluna de cabeçalho e contém os nomes e números de cada etapa. A segunda coluna contém mais instruções escritas. A terceira coluna contém os números correspondentes às etapas e instruções escritas. Na linha superior, a primeira célula diz: “Etapa 1. Localize o valor posicional fornecido com uma seta. Todos os dígitos à esquerda não mudam.” Na segunda célula, as instruções dizem: “Localize a casa das centenas em 23.658”. Na terceira célula, há o número 23.658 com uma seta apontando para o dígito 6, rotulando-o como “centenas de lugares”.Uma linha abaixo, as instruções na primeira célula dizem: “Etapa 2. Sublinhe o dígito à direita do valor posicional fornecido.” Na segunda célula, as instruções dizem: “Sublinhe o 5, que está à direita da casa das centenas”. Na terceira célula, há o número 23.658 novamente, a mesma seta apontando para o dígito 6, rotulando-o como a casa das centenas. O 5 também está sublinhado nesta célula.Uma linha abaixo, a primeira célula diz: “Etapa 3. Esse dígito é maior ou igual a 5? Sim — adicione 1 ao dígito no valor posicional fornecido. Não, não altere o dígito no valor posicional fornecido.” Na segunda célula, as instruções dizem: “Adicione 1 ao 6 na casa das centenas, já que 5 é maior ou igual a 5”. A terceira célula contém o número 23.658 novamente, com uma seta apontando para o dígito 6 e o texto “adicionar 1”. Há também um colchete sob os dígitos 5 e 8, com uma seta apontando para eles e o texto “substituir por 0s”.Na linha inferior, a primeira célula diz: “Etapa 4. Substitua todos os dígitos à direita do valor posicional fornecido por zeros. Então, 23.700 são arredondados para a centena mais próxima.” Na segunda célula, as instruções dizem: “Substitua todos os dígitos à direita da casa das centenas por zeros”. A terceira célula contém o número 23.700, que alcançamos arredondando o número 23.658 para a centena mais próxima.

    Exercício\(\PageIndex{11}\)

    Arredonde para a centena mais próxima: 17.852.

    Resposta

    17.900

    Exercício\(\PageIndex{12}\)

    Arredonde para a centena mais próxima: 468.751.

    Resposta

    468.800

    NÚMEROS INTEIROS REDONDOS.
    1. Localize o valor posicional fornecido e marque-o com uma seta. Todos os dígitos à esquerda da seta não mudam.
    2. Sublinhe o dígito à direita do valor posicional fornecido.
    3. Esse dígito é maior ou igual a 5?
      • Sim — adicione 11 ao dígito no valor posicional fornecido.
      • Não — não altere o dígito no valor posicional fornecido.
    4. Substitua todos os dígitos à direita do valor posicional fornecido por zeros.
    Exercício\(\PageIndex{13}\)

    Arredonde 103.978103.978 para o mais próximo:

    1. cem
    2. mil
    3. dez mil
    Resposta
    1.
    Localize a casa das centenas em 103.978. .
    Sublinhe o dígito à direita da casa das centenas. .
    Como 7 é maior ou igual a 5, adicione 1 ao 9. Substitua todos os dígitos à direita da casa das centenas por zeros. .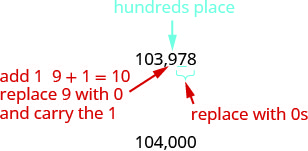
      Então, 104.000 é 103.978 arredondado para a centena mais próxima.
    2.
    Localize a casa dos milhares e sublinhe o dígito à direita da casa dos milhares. .
    Como 9 é maior ou igual a 5, adicione 1 ao 3. Substitua todos os dígitos à direita da casa das centenas por zeros. .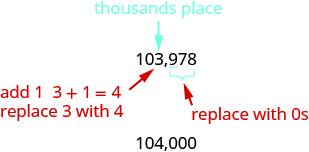
      Então, 104.000 é 103.978 arredondado para o milhar mais próximo.
    3.
    Localize a casa dos dez milhares e sublinhe o dígito à direita da casa dos dez milhares. .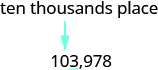
    Como 3 é menor que 5, deixamos o 0 como está e substituímos os dígitos à direita por zeros. .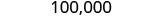
      Então, 100.000 é 103.978 arredondado para os dez mil mais próximos.
    Exercício\(\PageIndex{14}\)

    Arredonde 206.981 para o mais próximo: 1,cento e 2. mil 3. dez mil.

    Resposta
    1. 207.000
    2. 207.000
    3. 210.000
    Exercício\(\PageIndex{15}\)

    Arredonde 784.951 para o mais próximo: 1,cento e 2. mil 3. dez mil.

    Resposta
    1. 785.000
    2. 785.000
    3. 780.000

    Identifique múltiplos e aplique testes de divisibilidade

    Os números 2, 4, 6, 8, 10 e 12 são chamados de múltiplos de 2. Um múltiplo de 2 pode ser escrito como o produto de um número de contagem e 2.

    Um diagrama composto por duas linhas de números. A linha superior diz “2, 4, 6, 8, 10, 12”, seguida por uma elipse. Abaixo de 2 é 2 vezes 1, abaixo de 4 é 2 vezes 2, abaixo de 6 é 2 vezes 3, abaixo de 8 é 2 vezes 4, abaixo de 10 é 2 vezes 5 e abaixo de 12 está 2 vezes 6.
    Figura\(\PageIndex{4}\)

    Da mesma forma, um múltiplo de 3 seria o produto de um número de contagem e 3.

    Um diagrama composto por duas linhas de números. A linha superior diz “3, 6, 9, 12, 15, 18", seguida por uma elipse. Abaixo de 3 é 3 vezes 1, abaixo de 6 é 3 vezes 2, abaixo de 9 é 3 vezes 3, abaixo de 12 é 3 vezes 4, abaixo de 15 é 3 vezes 5 e abaixo de 18 é 3 vezes 6.
    Figura\(\PageIndex{5}\)

    Podemos encontrar os múltiplos de qualquer número continuando esse processo.

    Nota

    Fazer a atividade de Matemática Manipulativa “Múltiplos” ajudará você a desenvolver uma melhor compreensão dos múltiplos.

    A tabela\(\PageIndex{1}\) mostra os múltiplos de 2 a 9 para os primeiros 12 números de contagem.

    Número de contagem 1 2 3 4 5 6 7 8 9 10 11 12
    Múltiplos de 2 2 4 6 8 10 12 14 16 18 20 22 24
    Múltiplos de 3 3 6 9 12 15 18 21 24 27 30 33 36
    Múltiplos de 4 4 8 12 16 20 24 28 32 36 40 44 48
    Múltiplos de 5 5 10 15 20 25 30 35 40 45 50 55 60
    Múltiplos de 6 6 12 18 24 30 36 42 48 54 60 66 72
    Múltiplos de 7 7 14 21 28 35 42 49 56 63 70 77 84
    Múltiplos de 8 8 16 24 32 40 48 56 64 72 80 88 96
    Múltiplos de 9 9 18 27 36 45 54 63 72 81 90 99 108
    Múltiplos de 10 10 20 30 40 50 60 70 80 90 100 110 120
    Tabela\(\PageIndex{1}\)
    MÚLTIPLO DE UM NÚMERO

    Um número é um múltiplo de\(n\) se for o produto de um número de contagem\(n\) e.

    Outra forma de dizer que 15 é múltiplo de 3 é dizer que 15 é divisível por 3. Isso significa que quando dividimos 3 em 15, obtemos um número de contagem. Na verdade,\(15\div 3\) é 5, então 15 é\(5\cdot3\).

    DIVISÍVEL POR UM NÚMERO

    Se um número\(m\) for múltiplo de\(n\), então\(m\) é divisível por\(n\)

    Veja os múltiplos de\(5\) na Tabela\(\PageIndex{1}\). Todos eles terminam em 5 ou 0. Números com o último dígito de 5 ou 0 são divisíveis por 5. Procurando outros padrões na Tabela\(\PageIndex{1}\) que mostrem múltiplos dos números de 2 a 9, podemos descobrir os seguintes testes de divisibilidade:

    TESTES DE DIVISIBILIDADE

    Um número é divisível por:

    • 2 se o último dígito for 0, 2, 4, 6 ou 8.
    • 3 se a soma dos dígitos for divisível por 3.
    • 5 se o último dígito for 5 ou 0.
    • 6 se for divisível por 2 e 3.
    • 10 se terminar com 0.
    Exercício\(\PageIndex{16}\)

    5625 é divisível por 2? Por 3? Por 5? Até 6? Por 10?

    Resposta

    \[\begin{array} {ll} {\text{Is 5625 divisible by 2?}} &{} \\ {\text{Does it end in 0, 2, 4, 6, or 8?}} &{\text{No.}} \\ {} &{\text{5625 is not divisible by 2.}} \end{array}\]

    \[\begin{array} {ll} {\text{Is 5625 divisible by 3?}} &{} \\ {\text{What is the sum of the digits?}} &{5 + 6 + 2 + 5 = 18} \\ {\text{Is the sum divisible by 3?}} &{\text{Yes, 5625 is divisible by 3.}} \end{array}\]

    \[\begin{array} {ll} {\text{Is 5625 divisible by 5 or 10?}} &{} \\ {\text{What is the last digit? It is 5.}} &{\text{5625 is divisible by 5 but not by 10.}} \end{array}\]

    \[\begin{array} {ll} {\text{Is 5625 divisible by 6?}} &{} \\ {\text{Is it divisible by both 2 and 3?}} &{\text{No, 5625 is not divisible by 2, so 5625 is }} \\ {} &{\text{not divisible by 6.}}\end{array}\]

    Exercício\(\PageIndex{17}\)

    Determine se 4.962 é divisível por 2, por 3, por 5, por 6 e por 10.

    Resposta

    por 2, 3 e 6

    Exercício\(\PageIndex{18}\)

    Determine se 3.765 é divisível por 2, por 3, por 5, por 6 e por 10.

    Resposta

    por 3 e 5

    Encontre fatorizações primárias e múltiplos menos comuns

    Em matemática, muitas vezes há várias maneiras de falar sobre as mesmas ideias. Até agora, vimos que se\(m\) for um múltiplo de\(n\), podemos dizer que\(m\) é divisível por\(n\). Por exemplo, como 72 é um múltiplo de 8, dizemos que 72 é divisível por 8. Como 72 é um múltiplo de 9, dizemos que 72 é divisível por 9. Podemos expressar isso ainda de outra forma.

    \(8\cdot 9=72\)Pois, dizemos que 8 e 9 são fatores de 72. Quando escrevemos\(72=8\cdot 9\), dizemos que fatoramos 72.

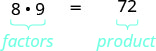
    Uma imagem mostra a equação 8 vezes 9 igual a 72. Escrito abaixo, a expressão 8 vezes 9 está um colchete e a palavra “fatores”, enquanto escrita abaixo de 72, é um colchete horizontal e a palavra “produto”.
    Figura\(\PageIndex{6}\)

    Outras formas de fatorar 72 são\(1\cdot 72\)\(2\cdot 36\)\(3\cdot 24\),,\(4\cdot 18\)\(6\cdot 12\) e. Setenta e dois têm muitos fatores: 1, 2, 3, 4, 6, 8, 9, 12, 18, 36 e 72.

    FATORES

    Se\(a\cdot b=m\), então\(a\) e\(b\) são fatores de\(m\).

    Alguns números, como 72, têm muitos fatores. Outros números têm apenas dois fatores.

    Nota

    Fazer a atividade de Matemática Manipulativa “Multiplicação e Fatoração de Modelos” ajudará você a desenvolver uma melhor compreensão da multiplicação e fatoração.

    NÚMERO PRIMO E NÚMERO COMPOSTO

    Um número primo é um número de contagem maior que 1, cujos únicos fatores são 1 e ele próprio.

    Um número composto é um número de contagem que não é primo. Um número composto tem fatores diferentes de 1 e ele próprio.

    Nota

    Fazer a atividade de Matemática Manipulativa “Números Primos” ajudará você a desenvolver uma melhor compreensão dos números primos.

    Os números de contagem de 2 a 19 estão listados na Figura\(\PageIndex{7}\), com seus fatores. Certifique-se de concordar com o rótulo “principal” ou “composto” para cada um!

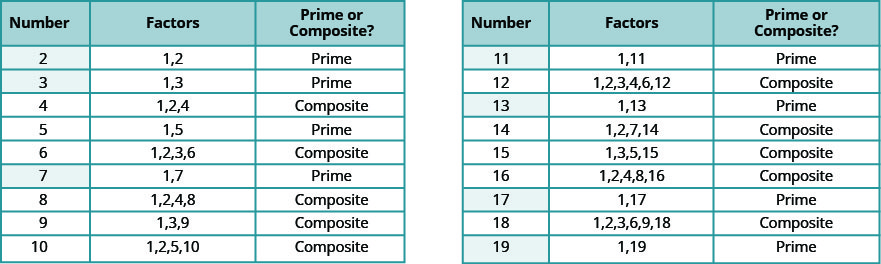
    Uma tabela é mostrada com onze linhas e sete colunas. A primeira linha é uma linha de cabeçalho e cada célula rotula o conteúdo da coluna abaixo dela. Na linha do cabeçalho, as três primeiras células são lidas da esquerda para a direita “Número”, “Fatores” e “Primo ou Composto?” A quarta coluna inteira está em branco. As últimas três células são lidas da esquerda para a direita “Número”, “Fator” e “Primo ou Composto?” novamente. Em cada linha subsequente, a primeira célula contém um número, a segunda contém seus fatores e a terceira indica se o número é primo ou composto. As três colunas à esquerda da coluna central em branco contêm essas informações para o número 2 a 10, e as três colunas à direita da coluna central em branco contêm essas informações para o número 11 a 19. No lado esquerdo da coluna em branco, na primeira linha abaixo da linha do cabeçalho, as células são lidas da esquerda para a direita: “2”, “1,2” e “Prime”. Na próxima linha, as células são lidas da esquerda para a direita: “3”, “1,3” e “Prime”. Na próxima linha, as células são lidas da esquerda para a direita: “4”, “1,2,4” e “Composto”. Na próxima linha, as células são lidas da esquerda para a direita: “5”, “1,5” e “Prime”. Na próxima linha, as células são lidas da esquerda para a direita: “6”, “1,2,3,6” e “Composto”. Na próxima linha, as células são lidas da esquerda para a direita: “7”, “1,7” e “Prime”. Na próxima linha, as células são lidas da esquerda para a direita: “8”, “1,2,4,8” e “Composto”. Na próxima linha, as células são lidas da esquerda para a direita: “9”, “1,3,9” e “Composto”. Na linha inferior, as células são lidas da esquerda para a direita: “10”, “1,2,5,10” e “Composto”. No lado direito da coluna em branco, na primeira linha abaixo da linha do cabeçalho, as células são lidas da esquerda para a direita: “11”, “1,11” e “Prime”. Na próxima linha, as células são lidas da esquerda para a direita: “12”, “1,2,3,4,6,12” e “Composto”. Na próxima linha, as células são lidas da esquerda para a direita: “13”, “1,13” e “Prime”. Na próxima linha, as células lêem da esquerda para a direita “14”, “1,2,7,14” e “Composto”. Na próxima linha, as células são lidas da esquerda para a direita: “15”, “1,3,5,15” e “Composto”. Na próxima linha, as células são lidas da esquerda para a direita: “16”, “1,2,4,8,16” e “Composto”. Na próxima linha, as células são lidas da esquerda para a direita, “17”, “1,17” e “Prime”. Na próxima linha, as células são lidas da esquerda para a direita, “18”, “1,2,3,6,9,18” e “Composto”. Na linha inferior, as células são lidas da esquerda para a direita: “19”, “1,19” e “Prime”.
    Figura\(\PageIndex{7}\)

    Os números primos menores que 20 são 2, 3, 5, 7, 11, 13, 17 e 19. Observe que o único número primo par é 2.

    Um número composto pode ser escrito como um produto exclusivo de números primos. Isso é chamado de fatoração primária do número. Encontrar a fatoração primária de um número composto será útil posteriormente neste curso.

    FATORAÇÃO PRIMÁRIA

    A fatoração primária de um número é o produto de números primos que é igual ao número.

    Para encontrar a fatoração primária de um número composto, encontre quaisquer dois fatores do número e use-os para criar duas ramificações. Se um fator for primo, essa ramificação estará completa. Circule aquele primo!

    Se o fator não for primo, encontre dois fatores do número e continue o processo. Depois que todos os ramos tiverem circulado números primos no final, a fatoração estará concluída. O número composto agora pode ser escrito como um produto de números primos.

    Exercício\(\PageIndex{19}\)

    Fator 48.

    Resposta

    Essa figura é uma tabela que tem três colunas e quatro linhas. A primeira coluna é uma coluna de cabeçalho e contém os nomes e números de cada etapa. A segunda coluna contém mais instruções escritas e um pouco de matemática. A terceira coluna contém a maior parte do trabalho matemático correspondente às etapas e instruções escritas. Na linha superior, a primeira célula diz: “Etapa 1. Encontre dois fatores cujo produto é o número fornecido. Use esses números para criar duas ramificações.” A segunda célula contém a equação algébrica 48 é igual a 2 vezes 24. Na terceira célula, há uma árvore fatorial com 48 na parte superior. Duas ramificações descem de 48 e terminam em 2 e 24, respectivamente.Uma linha abaixo, as instruções na primeira célula dizem: “Etapa 2. Se um fator for primo, essa ramificação estará completa. Circule o primo.” Na segunda célula, as instruções dizem: “2 é primo. Circule o primo.” Na terceira célula, a árvore de fatores da etapa 1 é repetida, mas a 2 na parte inferior da árvore agora está circulada.Uma linha abaixo, a primeira célula diz: “Etapa 3. Se um fator não for primo, escreva-o como produto de dois fatores e continue o processo.” Na segunda célula, as instruções dizem: “24 não é primo. Divida-o em mais dois fatores.” A terceira célula contém a árvore fatorial original, com 48 na parte superior e duas ramificações apontando para baixo terminando em 2, que está sublinhado, e 24. Mais duas ramificações descem de 24 e terminam em 4 e 6, respectivamente. Uma linha abaixo, as instruções no meio da célula dizem que “4 e 6 não são primos. Divida cada um deles em dois fatores.” Na célula à direita, a árvore de fatores é repetida mais uma vez. Dois ramos descem do 4 e terminam em 2 e 2. Ambos os 2s estão circulados. Mais dois galhos descem de 6 e terminam em 2 e 3, ambos circulados. As instruções à esquerda dizem que “2 e 3 são primos, então circule-os”.Na linha inferior, a primeira célula diz: “Etapa 4. Escreva o número composto como o produto de todos os números primos circulados.” A segunda célula é deixada em branco. A terceira célula contém a equação algébrica 48 é igual a 2 vezes 2 vezes 2 vezes 2 vezes 3.

    Dizemos que\(2\cdot 2\cdot 2\cdot 2\cdot 3\) é a fatoração primária de 48. Geralmente escrevemos os números primos em ordem crescente. Não se esqueça de multiplicar os fatores para verificar sua resposta!

    Se primeiro fatorássemos 48 de uma maneira diferente, por exemplo\(6\cdot 8\), o resultado ainda seria o mesmo. Conclua a fatoração primária e verifique isso por si mesmo.

    Exercício\(\PageIndex{20}\)

    Encontre a fatoração primária de 80.

    Resposta

    \(2\cdot 2\cdot 2\cdot 2\cdot 5\)

    Exercício\(\PageIndex{21}\)

    Encontre a fatoração primária de 60.

    Resposta

    \(2\cdot 2\cdot 3\cdot 5\)

    ENCONTRE A FATORAÇÃO PRIMÁRIA DE UM NÚMERO COMPOSTO.
    1. Encontre dois fatores cujo produto é o número fornecido e use esses números para criar duas ramificações.
    2. Se um fator for primo, essa ramificação estará completa. Circule o primo, como um broto na árvore.
    3. Se um fator não for primo, escreva-o como produto de dois fatores e continue o processo.
    4. Escreva o número composto como o produto de todos os números primos circulados.
    Exercício\(\PageIndex{22}\)

    Encontre a fatoração primária de 252.

    Resposta
    Etapa 1. Encontre dois fatores cujo produto é 252. 12 e 21 não são primos.

    Divida 12 e 21 em mais dois fatores. Continue até que todos os números primos sejam fatorados.    		 .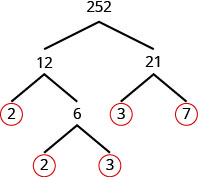
    Etapa 2. Escreva 252 como o produto de todos os números primos circulados.

    \(252=2\cdot 2\cdot 3\cdot 3\cdot 7\)
    Exercício\(\PageIndex{23}\)

    Encontre a fatoração primária de 126.

    Resposta

    \(2\cdot 3\cdot 3\cdot 7\)

    Exercício\(\PageIndex{24}\)

    Encontre a fatoração primária de 294.

    Resposta

    \(2\cdot 3\cdot 7\cdot 7\)

    Uma das razões pelas quais analisamos múltiplos e números primos é usar essas técnicas para encontrar o mínimo múltiplo comum de dois números. Isso será útil quando somarmos e subtrairmos frações com denominadores diferentes. Dois métodos são usados com mais frequência para encontrar o mínimo múltiplo comum e examinaremos os dois.

    O primeiro método é o Método de Listagem de Múltiplos. Para encontrar o mínimo múltiplo comum de 12 e 18, listamos os primeiros múltiplos de 12 e 18:

    Duas linhas de números são mostradas. A primeira linha começa com 12, seguida por dois pontos, depois 12, 24, 36, 48, 60, 72, 84, 96, 108 e uma elipse. 36, 72 e 108 estão escritos em negrito em vermelho. A segunda linha começa com 18, seguida por dois pontos, depois 18, 36, 54, 72, 90, 108 e uma elipse. Novamente, os números 36, 72 e 108 estão escritos em negrito em vermelho. Na linha abaixo está a frase “Múltiplos comuns”, dois pontos e os números 36, 72 e 108, escritos em vermelho. Uma linha abaixo está a frase “Least Common Multiple”, dois pontos e o número 36, escrito em azul.
    Figura\(\PageIndex{8}\)

    Observe que alguns números aparecem nas duas listas. Eles são os múltiplos comuns de 12 e 18.

    Vemos que os primeiros múltiplos comuns de 12 e 18 são 36, 72 e 108. Como 36 é o menor dos múltiplos comuns, nós o chamamos de múltiplo menos comum. Costumamos usar a abreviatura LCM.

    MÚLTIPLO MENOS COMUM

    O mínimo múltiplo comum (LCM) de dois números é o menor número que é múltiplo de ambos os números.

    A caixa de procedimentos lista as etapas a serem seguidas para encontrar o LCM usando o método de fatores primos que usamos acima para 12 e 18.

    ENCONTRE O MÚLTIPLO MENOS COMUM LISTANDO MÚLTIPLOS.
    1. Liste vários múltiplos de cada número.
    2. Procure o menor número que aparece nas duas listas.
    3. Esse número é o LCM.
    Exercício\(\PageIndex{25}\)

    Encontre o mínimo múltiplo comum de 15 e 20 listando múltiplos.

    Resposta
    Faça listas dos primeiros múltiplos de 15 e de 20 e use-as para encontrar o múltiplo menos comum. .
    Procure o menor número que aparece nas duas listas. O primeiro número a aparecer nas duas listas é 60, então 60 é o múltiplo menos comum de 15 e 20.

    Observe que 120 também está nas duas listas. É um múltiplo comum, mas não é o mínimo múltiplo comum.

    Exercício\(\PageIndex{26}\)

    Encontre o mínimo múltiplo comum listando múltiplos: 9 e 12.

    Resposta

    \(36\)

    Exercício\(\PageIndex{27}\)

    Encontre o mínimo múltiplo comum listando os múltiplos: 18 e 24.

    Resposta

    \(72\)

    Nosso segundo método para encontrar o mínimo múltiplo comum de dois números é usar o Método dos Fatores Primos. Vamos encontrar o LCM de 12 e 18 novamente, desta vez usando seus fatores primos.

    Exercício\(\PageIndex{28}\)

    Encontre o Mínimo Múltiplo Comum (LCM) de 12 e 18 usando o método dos fatores primos.

    Resposta

    Essa figura é uma tabela que tem três colunas e quatro linhas. A primeira coluna é uma coluna de cabeçalho e contém os nomes e números de cada etapa. A segunda coluna contém mais instruções escritas e um pouco de matemática. A terceira coluna contém a maior parte do trabalho matemático correspondente às etapas e instruções escritas. Na linha superior, a primeira célula diz: “Etapa 1. Escreva cada número como um produto de números primos.” A segunda célula é deixada em branco. Na terceira célula, há duas árvores fatoriais. Na primeira árvore fatorial, dois galhos descem de 18 e terminam em 3 e 6, respectivamente. O 3 é primo e, portanto, circulado. Mais dois galhos descem do 6 e terminam em 2 e 3, ambos circulando. Na segunda árvore fatorial, dois galhos descem de 12 e terminam em 3 e 4. O 3 está circulado. Mais dois galhos descem de 4, terminando em 2 e 2, ambos circulados.Uma linha abaixo, as instruções na primeira célula dizem: “Etapa 2. Liste os números primos de cada número. Combine números primos verticalmente quando possível.” Na segunda célula, as instruções dizem: “Liste os números primos de 12. Liste os números primos de 18. Alinhe-se com os números primos de 12 quando possível. Se não, crie uma nova coluna.” A terceira célula contém a fatoração primária de 12 escrita como a equação 12 é igual a 2 vezes 2 vezes 3. Abaixo dessa equação está outra mostrando a fatoração primária de 18 escrita como a equação 18 é igual a 2 vezes 3 vezes 3. As duas equações se alinham verticalmente no símbolo igual. O primeiro 2 na fatoração primária de 12 se alinha com o 2 na fatoração primária de 18. Sob o segundo 2 na fatoração primária de 12, há uma lacuna na fatoração primária de 18. Abaixo do 3 na fatoração primária de 12 está o primeiro 3 na fatoração primária de 18. O segundo 3 na fatoração primária não tem fatores acima dele da fatoração primária de 12.Uma linha abaixo, as instruções na primeira célula dizem: “Diminua o número de cada coluna”. A segunda célula está em branco. A terceira célula contém as fatorizações primárias de 12 e 18 novamente, ilustradas como duas equações alinhadas exatamente como estavam antes. Desta vez, uma linha horizontal é desenhada sob a fatoração primária de 18. Abaixo dessa linha está a equação LCM igual a 2 vezes 2 vezes 3 vezes 3. As setas são desenhadas verticalmente da fatoração primária de 12 até a fatoração primária de 18 terminando na equação LCM. A primeira seta começa nos 2 primeiros na fatoração primária de 12 e continua até o 2 na fatoração primária de 18, terminando com os 2 primeiros no LCM. A segunda seta começa nas próximas 2 na fatoração primária de 12 e continua descendo pela lacuna na fatoração primária de 18, terminando com a segunda 2 no LCM. A terceira seta começa no 3 na fatoração primária de 12 e continua até os 3 primeiros na fatoração primária de 18, terminando com os 3 primeiros no LCM. A última seta começa no segundo 3 na fatoração primária de 18 e aponta para baixo para o segundo 3 no LCM.Na linha inferior da tabela, a primeira célula diz: “Etapa 4: Multiplique os fatores”. A segunda célula é banco. A terceira célula contém a equação LCM igual a 36.

    Observe que os fatores primos de\(12(2\cdot 2\cdot 3)\) e os fatores primos de\(18(2\cdot 3\cdot 3)\) estão incluídos no LCM\((2\cdot 2\cdot 3\cdot 3)\). Portanto, 36 é o múltiplo menos comum de 12 e 18.

    Ao combinar os números primos comuns, cada fator primo comum é usado apenas uma vez. Dessa forma, você tem certeza de que 36 é o múltiplo menos comum.

    Exercício\(\PageIndex{29}\)

    Encontre o LCM usando o método dos fatores primos: 9 e 12.

    Resposta

    \(36\)

    Exercício\(\PageIndex{30}\)

    Encontre o LCM usando o método dos fatores primos: 18 e 24.

    Resposta

    \(72\)

    ENCONTRE O MÚLTIPLO MENOS COMUM USANDO O MÉTODO DOS FATORES PRIMOS.
    1. Escreva cada número como um produto de números primos.
    2. Liste os números primos de cada número. Combine números primos verticalmente quando possível.
    3. Derrube as colunas.
    4. Multiplique os fatores.
    Exercício\(\PageIndex{31}\)

    Encontre o Mínimo Múltiplo Comum (LCM) de 24 e 36 usando o método dos fatores primos.

    Resposta
    Encontre os números primos de 24 e 36.
    Combine números primos verticalmente quando possível.

    Derrube todas as colunas.    		 .
    Multiplique os fatores. .
     

    O LCM de 24 e 36 é 72.
    Exercício\(\PageIndex{32}\)

    Encontre o LCM usando o método dos fatores primos: 21 e 28.

    Resposta

    \(84\)

    Exercício\(\PageIndex{33}\)

    Encontre o LCM usando o método dos fatores primos: 24 e 32.

    Resposta

    \(96\)

    Nota

    Acesse este recurso on-line para obter instruções adicionais e praticar o uso de números inteiros. Você precisará habilitar o Java em seu navegador para usar o aplicativo.

    Conceitos chave

    • Valor posicional como na figura.
    • Nomear um número inteiro em palavras
      1. Comece à esquerda e nomeie o número em cada período, seguido pelo nome do período.
      2. Coloque vírgulas no número para separar os pontos.
      3. Não nomeie o ponto final.
    • Escreva um número inteiro usando dígitos
      1. Identifique as palavras que indicam períodos. (Lembre-se de que aquele período nunca tem nome.)
      2. Desenhe 3 espaços em branco para indicar o número de vagas necessárias em cada período. Separe os pontos por vírgulas.
      3. Nomeie o número em cada período e coloque os dígitos na posição correta do valor posicional.
    • Números inteiros redondos
      1. Localize o valor posicional fornecido e marque-o com uma seta. Todos os dígitos à esquerda da seta não mudam.
      2. Sublinhe o dígito à direita do valor posicional fornecido.
      3. Esse dígito é maior ou igual a 5?
        • Sim — adicione 1 ao dígito no valor posicional fornecido.
        • Não — não altere o dígito no valor posicional fornecido.
      4. Substitua todos os dígitos à direita do valor posicional fornecido por zeros.
    • Testes de divisibilidade: Um número é divisível por:
      • 2 se o último dígito for 0, 2, 4, 6 ou 8.
      • 3 se a soma dos dígitos for divisível por 3.
      • 5 se o último dígito for 5 ou 0.
      • 6 se for divisível por 2 e 3.
      • 10 se terminar com 0.
    • Encontre a fatoração primária de um número composto
      1. Encontre dois fatores cujo produto é o número fornecido e use esses números para criar duas ramificações.
      2. Se um fator for primo, essa ramificação estará completa. Circule o primo, como um broto na árvore.
      3. Se um fator não for primo, escreva-o como produto de dois fatores e continue o processo.
      4. Escreva o número composto como o produto de todos os números primos circulados.
    • Encontre o múltiplo menos comum listando múltiplos
      1. Liste vários múltiplos de cada número.
      2. Procure o menor número que aparece nas duas listas.
      3. Esse número é o LCM.
    • Encontre o múltiplo menos comum usando o método dos fatores primos
      1. Escreva cada número como um produto de números primos.
      2. Liste os números primos de cada número. Combine números primos verticalmente quando possível.
      3. Derrube as colunas.
      4. Multiplique os fatores.

    Glossário

    número composto
    Um número composto é um número de contagem que não é primo. Um número composto tem fatores diferentes de 1 e ele próprio.
    contando números
    Os números de contagem são os números 1, 2, 3,...
    divisível por um número
    Se um número\(m\) for múltiplo de\(n\), então\(m\) é divisível por\(n\). (Se 6 for um múltiplo de 3, então 6 é divisível por 3.)
    fatores
    Se\(a\cdot b=m\), então\(a\) e\(b\) são fatores de\(m\). Desde então\(3 \cdot 4 = 12\), 3 e 4 são fatores de 12.
    múltiplo menos comum
    O mínimo múltiplo comum de dois números é o menor número que é múltiplo de ambos os números.
    múltiplo de um número
    Um número é um múltiplo de\(n\) se for o produto de um número de contagem\(n\) e.
    linha numérica
    Uma linha numérica é usada para visualizar números. Os números na reta numérica ficam maiores à medida que vão da esquerda para a direita e menores à medida que vão da direita para a esquerda.
    origem
    A origem é o ponto rotulado como 0 em uma reta numérica.
    fatoração primária
    A fatoração primária de um número é o produto de números primos que é igual ao número.
    número primo
    Um número primo é um número de contagem maior que 1, cujos únicos fatores são 1 e ele próprio.
    números inteiros
    Os números inteiros são os números 0, 1, 2, 3,...