12.3: O produto Dot

Objetivos de

• Calcule o produto escalar de dois vetores fornecidos.
• Determine se dois vetores fornecidos são perpendiculares.
• Encontre os cossenos de direção de um determinado vetor.
• Explique o que significa a projeção vetorial de um vetor em outro vetor e descreva como computá-la.
• Calcule o trabalho realizado por uma determinada força.

Se aplicarmos uma força a um objeto para que o objeto se mova, dizemos que o trabalho é feito pela força. Anteriormente, observávamos uma força constante e presumíamos que a força era aplicada na direção do movimento do objeto. Nessas condições, o trabalho pode ser expresso como o produto da força que atua sobre um objeto e da distância que o objeto se move. Neste capítulo, no entanto, vimos que tanto a força quanto o movimento de um objeto podem ser representados por vetores.

Nesta seção, desenvolvemos uma operação chamada produto escalar, que nos permite calcular o trabalho no caso de o vetor de força e o vetor de movimento terem direções diferentes. O produto escalar nos diz essencialmente quanto do vetor de força é aplicado na direção do vetor de movimento. O produto escalar também pode nos ajudar a medir o ângulo formado por um par de vetores e a posição de um vetor em relação aos eixos coordenados. Ele ainda fornece um teste simples para determinar se dois vetores se encontram em um ângulo reto.

O produto Dot e suas propriedades

Já aprendemos como somar e subtrair vetores. Neste capítulo, investigamos dois tipos de multiplicação vetorial. O primeiro tipo de multiplicação vetorial é chamado de produto escalar, com base na notação que usamos para isso, e é definido da seguinte forma:

Definição: produto escalar

O produto escalar dos vetores\(\vecs{ u}=⟨u_1,u_2,u_3⟩\) e\(\vecs{ v}=⟨v_1,v_2,v_3⟩\) é dado pela soma dos produtos dos componentes

\[\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3. \nonumber \]

Observe que, se\(u\) e\(v\) forem vetores bidimensionais, calculamos o produto escalar de forma semelhante. Assim, se\(\vecs{ u}=⟨u_1,u_2⟩\) e\(\vecs{ v}=⟨v_1,v_2⟩,\) então

\[\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2. \nonumber \]

Quando dois vetores são combinados sob adição ou subtração, o resultado é um vetor. Quando dois vetores são combinados usando o produto escalar, o resultado é um escalar. Por esse motivo, o produto escalar costuma ser chamado de produto escalar. Também pode ser chamado de produto interno.

Exemplo\(\PageIndex{1}\): Calculating Dot Products

1. Encontre o produto escalar de\(\vecs{ u}=⟨3,5,2⟩\)\(\vecs{ v}=⟨−1,3,0⟩\) e.
2. Encontre o produto escalar de\(\vecs{ p}=10\hat{\textbf i}−4 \hat{\textbf j}+7 \hat{\textbf k}\) e\(\vecs{ q}=−2\hat{\textbf i}+\hat{\textbf j}+6\hat{\textbf k}.\)

Solução:

a. Substitua os componentes vetoriais na fórmula do produto escalar:

\[ \begin{align*} \vecs{ u}⋅\vecs{ v} &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &=3(−1)+5(3)+2(0) \\[4pt] &=−3+15+0 \\[4pt] &=12. \end{align*}\]

b. O cálculo é o mesmo se os vetores forem escritos usando vetores unitários padrão. Ainda temos três componentes para cada vetor para substituir na fórmula o produto escalar:

\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=p_1q_1+p_2q_2+p_3q_3 \\[4pt] &=10(−2)+(−4)(1)+(7)(6) \\[4pt] &=−20−4+42 \\[4pt] &=18.\end{align*}\]

Exercício\(\PageIndex{1}\)

Encontre\(\vecs{ u}⋅\vecs{ v}\), onde\(\vecs{ u}=⟨2,9,−1⟩\) e\(\vecs{ v}=⟨−3,1,−4⟩.\)

Dica

Multiplique os componentes correspondentes e adicione seus produtos.

Responda

\(7\)

Assim como a adição e subtração vetorial, o produto escalar tem várias propriedades algébricas. Provamos três dessas propriedades e deixamos o resto como exercícios.

Propriedades do produto Dot

Seja\(\vecs{ u}\)\(\vecs{ v}\), e\(\vecs{ w}\) seja vetores e\(c\) seja um escalar.

1. Propriedade comutativa\[\vecs{ u}⋅\vecs{ v}=\vecs{ v}⋅\vecs{ u} \nonumber \]
2. Propriedade distributiva\[\vecs{ u}⋅(\vecs{ v}+\vecs{ w})=\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ w} \nonumber \]
3. Propriedade associativa\[c(\vecs{ u}⋅\vecs{ v})=(c\vecs{ u})⋅\vecs{ v}=\vecs{ u}⋅(c\vecs{ v}) \nonumber \]
4. Propriedade de magnitude\[\vecs{ v}⋅\vecs{ v}=\|\vecs{ v}\|^2 \nonumber \]

Prova

Deixe\(\vecs{ u}=⟨u_1,u_2,u_3⟩\) e\(\vecs{ v}=⟨v_1,v_2,v_3⟩.\) depois

\[ \begin{align*} \vecs{ u}⋅\vecs{ v} &=⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &= v_1u_1+v_2u_2+v_3u_3 \\[4pt] &= ⟨v_1,v_2,v_3⟩⋅⟨u_1,u_2,u_3⟩ \\[4pt] &=\vecs{ v}⋅\vecs{ u}.\end{align*}\]

A propriedade associativa se parece com a propriedade associativa da multiplicação de números reais, mas preste muita atenção à diferença entre objetos escalares e vetoriais:

\[ \begin{align*} c(\vecs{ u}⋅\vecs{ v}) &=c(u_1v_1+u_2v_2+u_3v_3) \\[4pt] &=c(u_1v_1)+c(u_2v_2)+c(u_3v_3) \\[4pt] &=(cu_1)v_1+(cu_2)v_2+(cu_3)v_3 \\[4pt] &=⟨cu_1,cu_2,cu_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=c⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=(c\vecs{ u})⋅\vecs{ v}.\end{align*}\]

A prova disso\(c(\vecs{ u}⋅\vecs{ v})=\vecs{ u}⋅(c\vecs{ v})\) é semelhante.

A quarta propriedade mostra a relação entre a magnitude de um vetor e seu produto escalar consigo mesmo:

\[ \begin{align*} \vecs{ v}⋅\vecs{ v} &=⟨v_1,v_2,v_3⟩⋅⟨v_1,v_2,v_3⟩\\[4pt] &=(v_1)^2+(v_2)^2+(v_3)^2 \\[4pt] &=\left[\sqrt{(v_1)^2+(v_2)^2+(v_3)^2}\right]^2 \\[4pt] &=\|\vecs{ v}\|^2.\end{align*}\]

□

Observe que a definição do produto escalar rende\(\vecs{ 0}⋅\vecs{ v}=0.\) pela propriedade iv. if\(\vecs{ v}⋅\vecs{ v}=0,\) then\(\vecs{ v}=\vecs{ 0}.\)

Exemplo\(\PageIndex{2}\): Using Properties of the Dot Product

Deixe\(\vecs{ a}=⟨1,2,−3⟩\)\(\vecs{ b}=⟨0,2,4⟩\),\( \vecs{ c} =⟨5,−1,3⟩\) e.

Encontre cada um dos seguintes produtos.

1. \(( \vecs{ a} ⋅ \vecs{ b}) \vecs{ c} \)
2. \(\vecs{ a}⋅(2\vecs{ c})\)
3. \(\|\vecs{ b}\|^2\)

Solução

a. Observe que essa expressão solicita o múltiplo escalar de\(\vecs{ c}\) por\(\vecs{ a}⋅\vecs{ b}\):

\[ \begin{align*} (\vecs{ a}⋅\vecs{ b})\vecs{ c} &=(⟨1,2,−3⟩⋅⟨0,2,4⟩)⟨5,−1,3⟩ \\[4pt] &=(1(0)+2(2)+(−3)(4))⟨5,−1,3⟩ \\[4pt] &=−8⟨5,−1,3⟩ \\[4pt] &= ⟨−40,8,−24⟩.\end{align*}\]

b. Essa expressão é um produto escalar do múltiplo vetorial\(\vecs{ a}\) e escalar 2\(\vecs{ c}\):

\[ \begin{align*} \vecs{ a}⋅(2\vecs{ c}) &=2(\vecs{ a}⋅\vecs{ c}) \\[4pt] &=2(⟨1,2,−3⟩⋅⟨5,−1,3⟩) \\[4pt] &=2(1(5)+2(−1)+(−3)(3)) \\[4pt] &=2(−6)=−12.\end{align*}\]

c. Simplificar essa expressão é uma aplicação direta do produto escalar:

\[ \begin{align*} \|\vecs{ b}\|^2 &=\vecs{ b}⋅\vecs{ b} \\[4pt] &=⟨0,2,4⟩⋅⟨0,2,4⟩\\[4pt] &=0^2+2^2+4^2\\[4pt] &=0+4+16\\[4pt] &=20.\end{align*}\]

Exercício\(\PageIndex{2}\)

Encontre os seguintes produtos para\(\vecs{ p}=⟨7,0,2⟩\)\(\vecs{ q}=⟨−2,2,−2⟩\),\(\vecs{ r}=⟨0,2,−3⟩\) e.

1. \((\vecs{ r}⋅\vecs{ p})\vecs{ q}\)
2. \(\|\vecs{ p}\|^2\)

Dica

\(\vecs{ r}⋅\vecs{ p}\)é um escalar.

Responda

\(a. \quad (\vecs{ r}⋅\vecs{ p})\vecs{ q}=⟨12,−12,12⟩; \quad b. \quad \|\vecs{ p}\|^2=53\)

Usando o produto escalar para encontrar o ângulo entre dois vetores

Quando dois vetores diferentes de zero são colocados na posição padrão, seja em duas ou três dimensões, eles formam um ângulo entre eles (Figura\(\PageIndex{1}\)). O produto escalar fornece uma maneira de encontrar a medida desse ângulo. Essa propriedade é resultado do fato de podermos expressar o produto escalar em termos do cosseno do ângulo formado por dois vetores.

Figura\(\PageIndex{1}\):\(θ\) Seja o ângulo entre dois vetores diferentes de zero\(\vecs{ u}\) e\(\vecs{ v}\) tal \(0≤θ≤π\).

Avaliando um produto Dot

O produto escalar de dois vetores é o produto da magnitude de cada vetor e do cosseno do ângulo entre eles:

\[\vecs{ u}⋅\vecs{ v}=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{evaldot} \]

Prova

Coloque os vetores\(\vecs{ u}\) e\(\vecs{ v}\) na posição padrão e considere o vetor\(\vecs{ v}−\vecs{ u}\) (Figura\(\PageIndex{2}\)). Esses três vetores formam um triângulo com comprimentos laterais\(‖\vecs{ u}‖,‖\vecs{ v}‖\),\(‖\vecs{ v}−\vecs{ u}‖\) e.

Figura\(\PageIndex{2}\): Os comprimentos dos lados do triângulo são dados pelas magnitudes dos vetores que formam o triângulo.

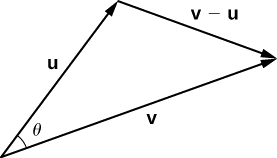
Lembre-se da trigonometria que a lei dos cossenos descreve a relação entre os comprimentos laterais do triângulo e o ângulo\(θ\). A aplicação da lei dos cossenos aqui dá

\[‖\vecs{ v}−\vecs{ u}‖^2=‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{eq20} \]

O produto escalar fornece uma maneira de reescrever o lado esquerdo da Equação\ ref {eq20}:

\[ \begin{align*} ‖\vecs{ v}−\vecs{ u}‖^2 &=(\vecs{ v}−\vecs{ u})⋅(\vecs{ v}−\vecs{ u}) \\[4pt] &=(\vecs{ v}−\vecs{ u})⋅\vecs{ v}−(\vecs{ v}−\vecs{ u})⋅\vecs{ u} \\[4pt] &=\vecs{ v}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}−\vecs{ v}⋅\vecs{ u}+\vecs{ u}⋅\vecs{ u} \\[4pt] &=\vecs{ v}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ u} \\[4pt] &=‖\vecs{ v}‖^2−2\vecs{ u}⋅\vecs{ v}+‖\vecs{ u}‖^2.\end{align*}\]

Substituindo na lei dos cossenos rendimentos

\[ \begin{align*} ‖\vecs{ v}−\vecs{ u}‖^2 &=‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] ‖\vecs{ v}‖^2−2\vecs{ u}⋅\vecs{ v}+‖\vecs{ u}‖^2 &= ‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] −2\vecs{ u}⋅\vecs{ v} &=−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] \vecs{ u}⋅\vecs{ v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \end{align*}\]

□

Podemos usar a forma do produto escalar na Equação\ ref {evaldot} para encontrar a medida do ângulo entre dois vetores diferentes de zero reorganizando a Equação\ ref {evaldot} para resolver o cosseno do ângulo:

\[\cos θ=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}. \label{dot2} \]

Usando essa equação, podemos encontrar o cosseno do ângulo entre dois vetores diferentes de zero. Como estamos considerando o menor ângulo entre os vetores, assumimos\(0°≤θ≤180°\) (ou\(0≤θ≤π\) se estamos trabalhando em radianos). O cosseno inverso é único nessa faixa, então podemos determinar a medida do ângulo\(θ\).

Exemplo\(\PageIndex{3}\): Finding the Angle between Two Vectors

Encontre a medida do ângulo entre cada par de vetores.

1. \(\mathbf{\hat i} + \mathbf{\hat j} + \mathbf{\hat k}\)e\(2\mathbf{\hat i} – \mathbf{\hat j} – 3\mathbf{\hat k}\)
2. \(⟨2,5,6⟩\)e\(⟨−2,−4,4⟩\)

Solução

a. Para encontrar o cosseno do ângulo formado pelos dois vetores, substitua os componentes dos vetores na Equação\ ref {dot2}:

\[ \begin{align*} \cos θ &=\dfrac{(\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k})⋅(2\mathbf{\hat i}−\mathbf{\hat j}−3\mathbf{\hat k})}{∥\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k}∥⋅∥2\mathbf{\hat i}−\mathbf{\hat j}−3\mathbf{\hat k}∥} \\[4pt] &=\dfrac{1(2)+(1)(−1)+(1)(−3)}{\sqrt{1^2+1^2+1^2}\sqrt{2^2+(−1)^2+(−3)^2}} \\[4pt] &=\dfrac{−2}{\sqrt{3}\sqrt{14}} =\dfrac{−2}{\sqrt{42}}. \end{align*}\]

Portanto,\(θ=\arccos\dfrac{−2}{\sqrt{42}}\) rad.

b. Comece encontrando o valor do cosseno do ângulo entre os vetores:

\[ \begin{align*} \cos θ &=\dfrac{⟨2,5,6⟩⋅⟨−2,−4,4⟩}{∥⟨2,5,6⟩∥⋅∥⟨−2,−4,4⟩∥} \\[4pt] &=\dfrac{2(−2)+(5)(−4)+(6)(4)}{\sqrt{2^2+5^2+6^2}\sqrt{(−2)^2+(−4)^2+4^2}} \\[4pt] &=\dfrac{0}{\sqrt{65}\sqrt{36}}=0.\end{align*}\]

Agora\(0≤θ≤π\),\(\cos θ=0\) e assim por diante\(θ=π/2\).

Exercício\(\PageIndex{3}\)

Encontre a medida do ângulo, em radianos, formado por vetores\(\vecs{ a}=⟨1,2,0⟩\)\(\vecs{ b}=⟨2,4,1⟩\) e. Arredonde para o centésimo mais próximo.

Dica

Use a equação\ ref {dot2}.

Responda

\(θ≈0.22\)rad

O ângulo entre dois vetores pode ser agudo\((−1<\cos θ<0)\),\((0<\cos θ<1),\) obtuso ou reto\((\cos θ=−1)\). Se\(\cos θ=1\) sim, então os dois vetores têm a mesma direção. Se\(\cos θ=0\), então, os vetores, quando colocados na posição padrão, formarem um ângulo reto (Figura\(\PageIndex{3}\)). Podemos formalizar esse resultado em um teorema sobre vetores ortogonais (perpendiculares).

Figura\(\PageIndex{3}\): (a) Um ângulo agudo tem\(0<\cos θ<1\). (b) Um ângulo obtuso tem\(−1<\cos θ<0.\) (c) Uma linha reta tem\(\cos θ=−1\). (d) Se os vetores tiverem a mesma direção,\(\cos θ=1\). (e) Se os vetores forem ortogonais (perpendiculares),\(\cos θ=0.\)

Vetores ortogonais

Os vetores diferentes de zero\(\vecs{u}\) e\(\vecs{v}\) são vetores ortogonais se e somente se\(\vecs{u}⋅\vecs{v}=0.\)

Prova

\(\vecs{u}\)Sejam vetores diferentes de zero e\(θ\) denotem o ângulo entre eles.\(\vecs{v}\) Primeiro, suponha\(\vecs{u}⋅\vecs{v}=0.\) Então

\[‖\vecs{u}‖‖\vecs{v}‖\cos θ=0. \nonumber \]

No entanto,\(‖\vecs{u}‖≠0\) e\(‖\vecs{v}‖≠0,\) por isso devemos ter feito isso\(\cos θ=0\). Portanto\(θ=90°\), e os vetores são ortogonais.

Agora suponha\(\vecs{u}\) e\(\vecs{v}\) sejam ortogonais. Então,\(θ=90°\) e nós temos

\[ \begin{align*} \vecs{u}⋅\vecs{v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖\cos 90° \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖(0) \\[4pt] &=0. \end{align*}\]

□

Cada um dos termos ortogonal, perpendicular e normal indica que objetos matemáticos estão se cruzando em ângulos retos. O uso de cada termo é determinado principalmente por seu contexto. Dizemos que os vetores são ortogonais e as linhas são perpendiculares. O termo normal é usado com mais frequência ao medir o ângulo feito com um plano ou outra superfície.

Exemplo\(\PageIndex{4}\): Identifying Orthogonal Vectors

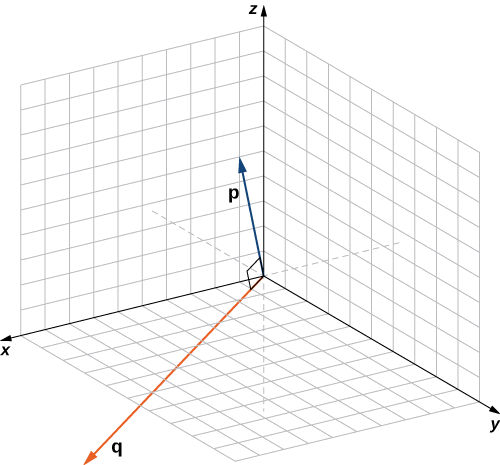
Determine se\(\vecs{p}=⟨1,0,5⟩\) e\(\vecs{q}=⟨10,3,−2⟩\) são vetores ortogonais.

Solução

Usando a definição, precisamos apenas verificar o produto escalar dos vetores:

\[ \vecs{ p}⋅\vecs{ q}=1(10)+(0)(3)+(5)(−2)=10+0−10=0. \nonumber \]

Porque\(\vecs{p}⋅\vecs{q}=0,\) os vetores são ortogonais (Figura\(\PageIndex{4}\)).

Figura\(\PageIndex{4}\): Vetores\(\vecs{ p}\) e\(\vecs{ q}\) formam um ângulo reto quando seus pontos iniciais estão alinhados.

Exercício\(\PageIndex{4}\)

Para qual valor de\(x\) é\(\vecs{ p}=⟨2,8,−1⟩\) ortogonal a\(\vecs{ q}=⟨x,−1,2⟩\)?

Dica

Vetores\(\vecs{ p}\) e\(\vecs{ q}\) são ortogonais se e somente se\(\vecs{ p}⋅\vecs{ q}=0\).

Responda

\(x=5\)

Exemplo\(\PageIndex{5}\): Measuring the Angle Formed by Two Vectors

Vamos\(\vecs{ v}=⟨2,3,3⟩.\) encontrar as medidas dos ângulos formados pelos seguintes vetores.

1. \(\vecs{ v}\)e\(\mathbf{\hat i}\)
2. \(\vecs{ v}\)e\(\mathbf{\hat j}\)
3. \(\vecs{ v}\)e\(\mathbf{\hat k}\)

Solução

a.Seja α o ângulo formado por\(\vecs{ v}\) e\(\mathbf{\hat i}\):

\[ \begin{align*} \cos{α} &=\dfrac{\vecs{ v}⋅\mathbf{\hat i}}{‖\vecs{ v}‖⋅\|\mathbf{\hat i}\|}=\dfrac{⟨2,3,3⟩⋅⟨1,0,0⟩}{\sqrt{2^2+3^2+3^2}\sqrt{1}}=\dfrac{2}{\sqrt{22}} \\[4pt] α &=\arccos\dfrac{2}{\sqrt{22}}≈1.130\,\text{rad.} \end{align*}\]

b. Seja β representar o ângulo formado por\(\vecs{ v}\) e\(\mathbf{\hat j}\):

\[ \begin{align*} \cos{β} &=\dfrac{\vecs{ v}⋅\mathbf{\hat j}}{‖\vecs{ v}‖⋅\|\mathbf{\hat j}\|}=\dfrac{⟨2,3,3⟩⋅⟨0,1,0⟩}{\sqrt{2^2+3^2+3^2}\sqrt{1}}=\dfrac{3}{\sqrt{22}} \\[4pt] β &=\arccos\dfrac{3}{\sqrt{22}}≈0.877\,\text{rad.} \end{align*}\]

c. Permita que γ represente o ângulo formado por\(\vecs{ v}\) e\(\mathbf{\hat k}\):

\[ \begin{align*} \cos{γ} &=\dfrac{\vecs{ v}⋅\mathbf{\hat k}}{‖\vecs{ v}‖⋅\|\mathbf{\hat k}\|}=\dfrac{⟨2,3,3⟩⋅⟨0,0,1⟩}{\sqrt{2^2+3^2+3^2}\sqrt{1}}=\dfrac{3}{\sqrt{22}} \\[4pt]γ &=\arccos\dfrac{3}{\sqrt{22}}≈0.877\,\text{rad.} \end{align*}\]

Exercício\(\PageIndex{5}\)

Vamos\(\vecs{ v}=⟨3,−5,1⟩.\) encontrar a medida dos ângulos formados por cada par de vetores.

1. \(\vecs{ v}\)e\(\mathbf{\hat i}\)
2. \(\vecs{ v}\)e\(\mathbf{\hat j}\)
3. \(\vecs{ v}\)e\(\mathbf{\hat k}\)

Dica

\(\mathbf{\hat i}=⟨1,0,0⟩, \mathbf{\hat j}=⟨0,1,0⟩,\)e\(\mathbf{\hat k}=⟨0,0,1⟩\)

Responda

\(a. α≈1.04\)estrada; b.\(β≈2.58\) estrada; c.\(γ≈1.40\) rad

O ângulo que um vetor faz com cada um dos eixos coordenados, chamado ângulo de direção, é muito importante em cálculos práticos, especialmente em um campo como a engenharia. Por exemplo, na engenharia astronáutica, o ângulo em que um foguete é lançado deve ser determinado com muita precisão. Um erro muito pequeno no ângulo pode fazer com que o foguete saia centenas de quilômetros do curso. Os ângulos de direção geralmente são calculados usando o produto escalar e os cossenos dos ângulos, chamados de cossenos de direção. Portanto, definimos esses ângulos e seus cossenos.

Definição: ângulos de direção

Os ângulos formados por um vetor diferente de zero e os eixos coordenados são chamados de ângulos de direção para o vetor (Figura\(\PageIndex{5}\)). Os cossenos desses ângulos são chamados de cossenos de direção.

Figura\(\PageIndex{5}\):\(α\) O ângulo é formado pelo vetor\(\vecs{ v}\) e pelo vetor unitário\(\mathbf{\hat i}\). O ângulo β é formado pelo vetor\(\vecs{ v}\) e pelo vetor unitário\(\mathbf{\hat j}\). O ângulo γ é formado pelo vetor\(\vecs{ v}\) e pelo vetor unitário\(\mathbf{\hat k}\).

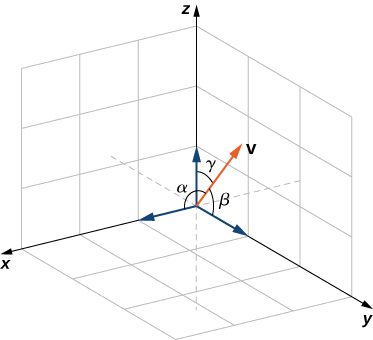
No exemplo\(\PageIndex{5}\), os cossenos de direção de\(\vecs{ v}=⟨2,3,3⟩\) são\(\cos α=\dfrac{2}{\sqrt{22}}, \cos β=\dfrac{3}{\sqrt{22}},\)\(\cos γ=\dfrac{3}{\sqrt{22}}\) e. Os ângulos de direção de\(\vecs{ v}\) são\(α=1.130\)\(β=0.877\) rad, rad e\(γ=0.877\) rad.

Até agora, nos concentramos principalmente em vetores relacionados à força, movimento e posição no espaço físico tridimensional. No entanto, os vetores são frequentemente usados de formas mais abstratas. Por exemplo, suponha que um vendedor de frutas venda maçãs, bananas e laranjas. Em um determinado dia, ele vende 30 maçãs, 12 bananas e 18 laranjas. Ele pode usar um vetor de quantidade\(\vecs{ q}=⟨30,12,18⟩,\) para representar a quantidade de frutas que vendeu naquele dia. Da mesma forma, ele pode querer usar um vetor de preço\(\vecs{ p}=⟨0.50,0.25,1⟩,\) para indicar que ele vende suas maçãs por 50 centavos cada, bananas por 25 centavos cada e laranjas por 1 dólar cada. Neste exemplo, embora ainda possamos representar graficamente esses vetores, não os interpretamos como representações literais da posição no mundo físico. Estamos simplesmente usando vetores para rastrear informações específicas sobre maçãs, bananas e laranjas.

Essa ideia pode parecer um pouco estranha, mas se simplesmente considerarmos os vetores como uma forma de ordenar e armazenar dados, descobrimos que eles podem ser uma ferramenta bastante poderosa. Voltando ao vendedor de frutas, vamos pensar no produto escalar,\(\vecs{ q}⋅\vecs{ p}\). Nós o calculamos multiplicando o número de maçãs vendidas (30) pelo preço por maçã (50¢), o número de bananas vendidas pelo preço por banana e o número de laranjas vendidas pelo preço por laranja. Em seguida, somamos todos esses valores. Então, neste exemplo, o produto escalar nos diz quanto dinheiro o vendedor de frutas tinha em vendas naquele dia específico.

Quando usamos vetores dessa forma mais geral, não há razão para limitar o número de componentes a três. E se o vendedor de frutas decidir começar a vender toranja? Nesse caso, ele gostaria de usar vetores quadridimensionais de quantidade e preço para representar o número de maçãs, bananas, laranjas e toranjas vendidas e seus preços unitários. Como era de se esperar, para calcular o produto escalar de vetores quadridimensionais, simplesmente adicionamos os produtos dos componentes como antes, mas a soma tem quatro termos em vez de três.

Exemplo\(\PageIndex{6}\): Using Vectors in an Economic Context

A AAA Party Supply Store vende convites, lembrancinhas, decorações e itens de food service, como pratos de papel e guardanapos. Quando a AAA compra seu estoque, ela paga 25 centavos por pacote para convites e lembrancinhas. As decorações custam 50 centavos de AAA cada, e os itens do serviço de alimentação custam 20 centavos por pacote. A AAA vende convites por $2,50 por pacote e lembrancinhas por $1,50 por pacote. As decorações são vendidas por $4,50 cada e os itens de food service por $1,25 por pacote.

Durante o mês de maio, a AAA Party Supply Store vende 1258 convites, 342 lembrancinhas, 2426 decorações e 1354 itens de food service. Use vetores e produtos escalonados para calcular quanto dinheiro a AAA ganhou em vendas durante o mês de maio. Quanto a loja obteve em lucro?

Solução

Os vetores de custo, preço e quantidade são

\[ \begin{align*} \vecs{ c} &=⟨0.25,0.25,0.50,0.20⟩ \\[4pt] \vecs{ p} &=⟨2.50,1.50,4.50,1.25⟩ \\[4pt] \vecs{ q} &=⟨1258,342,2426,1354⟩. \end{align*}\]

As vendas de AAA para o mês de maio podem ser calculadas usando o produto escalar\(\vecs{ p}⋅\vecs{ q}\). Nós temos

\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=⟨2.50,1.50,4.50,1.25⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] &=3145+513+10917+1692.5 \\[4pt] &= 16267.5. \end{align*}\]

Então, a AAA arrecadou $16.267,50 durante o mês de maio. Para calcular o lucro, devemos primeiro calcular quanto a AAA pagou pelos itens vendidos. Usamos o produto\(\vecs{c}⋅\vecs{q}\) escalar para obter

\[ \begin{align*} \vecs{ c}⋅\vecs{ q} &=⟨0.25,0.25,0.50,0.20⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] &=314.5+85.5+1213+270.8 \\[4pt] &=1883.8. \end{align*}\]

Então, a AAA pagou $1.883,80 pelos itens que vendeu. Seu lucro, então, é dado por

\[\vecs{ p}⋅\vecs{ q}−\vecs{ c}⋅\vecs{ q}=16267.5−1883.8 =14383.7. \nonumber \]

Portanto, a AAA Party Supply Store faturou $14.383,70 em maio.

Exercício\(\PageIndex{6}\)

Em 1º de junho, a AAA Party Supply Store decidiu aumentar o preço que cobra pelas lembrancinhas para $2 por pacote. Eles também trocaram de fornecedor para seus convites e agora podem comprar convites por apenas 10 centavos por pacote. Todos os outros custos e preços permanecem os mesmos. Se a AAA vender 1408 convites, 147 lembrancinhas, 2112 decorações e 1894 itens de food service no mês de junho, use vetores e produtos pontuais para calcular suas vendas totais e lucros em junho.

Dica

Use vetores quadridimensionais para custo, preço e quantidade vendida.

Responda

Vendas = $15.685,50; lucro = $14.073,15

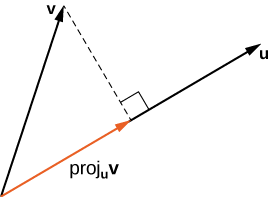
Projeções

Como vimos, a adição combina dois vetores para criar um vetor resultante. Mas e se recebermos um vetor e precisarmos encontrar seus componentes? Usamos projeções vetoriais para realizar o processo oposto; elas podem dividir um vetor em seus componentes. A magnitude de uma projeção vetorial é uma projeção escalar. Por exemplo, se uma criança estiver puxando a alça de um vagão em um ângulo de 55°, podemos usar projeções para determinar quanto da força na alça está realmente movendo o vagão para frente (\(\PageIndex{6}\)). Retornamos a esse exemplo e aprendemos como resolvê-lo depois de vermos como calcular projeções.

Figura\(\PageIndex{6}\): Quando uma criança puxa um vagão, somente o componente horizontal da força impulsiona o vagão para frente.

Definição: Vetor e projeção

A projeção vetorial de\(\vecs{ v}\) em cima\(\vecs{ u}\) é o vetor rotulado\(\text{proj}_\vecs{ u}\vecs{ v}\) na Figura\(\PageIndex{7}\). Tem o mesmo ponto inicial\(\vecs{ u}\)\(\vecs{ v}\) e a mesma direção que\(\vecs{ u}\), e representa o componente\(\vecs{ v}\) que atua na direção de\(\vecs{ u}\). Se\(θ\) representa o ângulo entre\(\vecs{ u}\) e\(\vecs{ v}\), então, pelas propriedades dos triângulos, sabemos que o comprimento de\(\text{proj}_\vecs{ u}\vecs{ v}\) é\(\|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs{ v}‖\cos θ.\) Ao expressar\(\cos θ\) em termos do produto escalar, isso se torna

\[ \|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs v‖\cos θ=‖\vecs{ v}‖\left(\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}\right)=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖.} \nonumber \]

Agora multiplicamos por um vetor unitário na direção de\(\vecs{ u}\) para obter\(\text{proj}_\vecs{ u}\vecs{ v}\):

\[\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\left(\dfrac{1}{‖\vecs{ u}‖}\vecs{ u}\right)=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}. \nonumber \]

O comprimento desse vetor também é conhecido como projeção escalar de\(\vecs{ v}\) onto\(\vecs{ u}\) e é indicado por

\[\|\text{proj}_\vecs{ u}\vecs{ v}\|=\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖.} \nonumber \]

Figura\(\PageIndex{7}\): A\(\vecs{ v}\) projeção de em cima\(\vecs{ u}\) mostra o componente do vetor\(\vecs{ v}\) na direção de\(\vecs{ u}\).

Exemplo\(\PageIndex{7}\): Finding Projections

Encontre a projeção de\(\vecs{ v}\) em cima\(\vecs{ u}\).

1. \(\vecs{v}=⟨3,5,1⟩\)e\(\vecs{u}=⟨−1,4,3⟩\)
2. \(\vecs{v}=3\mathbf{\hat i}−2\mathbf{\hat j}\)e\(\vecs{u}=\mathbf{\hat i}+6\mathbf{\hat j}\)

Solução

a. Substitua os componentes de\(\vecs{ v}\) e\(\vecs{ u}\) na fórmula da projeção:

\[\begin{align*} \text{proj}_\vecs{ u}\vecs{ v} &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{⟨−1,4,3⟩⋅⟨3,5,1⟩}{∥⟨−1,4,3⟩∥^2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{−3+20+3}{(−1)^2+4^2+3^2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{20}{26}⟨−1,4,3⟩ \\[4pt] &=⟨−\dfrac{10}{13},\dfrac{40}{13},\dfrac{30}{13}⟩. \end{align*}\]

b. Para encontrar a projeção bidimensional, basta adaptar a fórmula ao caso bidimensional:

\[\begin{align*} \text{proj}_\vecs{ u}\vecs{ v} &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{(\mathbf{\hat i}+6\mathbf{\hat j})⋅(3\mathbf{\hat i}−2\mathbf{\hat j})}{∥\mathbf{\hat i}+6\mathbf{\hat j}∥^2}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt] &= \dfrac{1(3)+6(−2)}{1^2+6^2}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt] &= −\dfrac{9}{37}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt] &= −\dfrac{9}{37}\mathbf{\hat i}−\dfrac{54}{37}\mathbf{\hat j}.\end{align*}\]

Às vezes, é útil decompor vetores, ou seja, dividir um vetor em uma soma. Esse processo é chamado de resolução de um vetor em componentes. As projeções nos permitem identificar dois vetores ortogonais com a soma desejada. Por exemplo, deixe\(\vecs{ v}=⟨6,−4⟩\) e deixe\(\vecs{ u}=⟨3,1⟩.\) Queremos decompor o vetor\(\vecs{ v}\) em componentes ortogonais, de forma que um dos vetores componentes tenha a mesma direção que\(\vecs{ u}\).

Primeiro, encontramos o componente que tem a mesma direção\(\vecs{ u}\) da\(\vecs{ v}\) projeção\(\vecs{ u}\). Deixe\(\vecs{ p}=\text{proj}_\vecs{ u}\vecs{ v}\). Então, nós temos

\[\begin{align*}\vecs{ p} =\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] = \dfrac{18−4}{9+1}\vecs{ u} \\[4pt] = \dfrac{7}{5}\vecs{ u}=\dfrac{7}{5}⟨3,1⟩=⟨\dfrac{21}{5},\dfrac{7}{5}⟩. \end{align*}\]

Agora considere o vetor\(\vecs{ q}=\vecs{ v}−\vecs{ p}.\) que temos

\[\begin{align*} \vecs{ q} =\vecs{ v}−\vecs{ p} \\[4pt] = ⟨6,−4⟩−⟨\dfrac{21}{5},\dfrac{7}{5}⟩ \\[4pt] = ⟨\dfrac{9}{5},−\dfrac{27}{5}⟩. \end{align*}\]

Claramente, pela forma como definimos\(\vecs{ q}\), temos\(\vecs{ v}=\vecs{ q}+\vecs{ p},\) e

\[\begin{align*}\vecs{ q}⋅\vecs{ p} =⟨\dfrac{9}{5},−\dfrac{27}{5}⟩⋅⟨\dfrac{21}{5},\dfrac{7}{5}⟩ \\[4pt] = \dfrac{9(21)}{25}+−\dfrac{27(7)}{25} \\[4pt] = \dfrac{189}{25}−\dfrac{189}{25}=0. \end{align*}\]

Portanto,\(\vecs{ q}\) e\(\vecs{ p}\) são ortogonais.

Exemplo\(\PageIndex{8}\): Resolving Vectors into Components

\(\vecs{ v}=⟨8,−3,−3⟩\)Expresse como uma soma de vetores ortogonais de forma que um dos vetores tenha a mesma direção que\(\vecs{ u}=⟨2,3,2⟩.\)

Solução

Vamos\(\vecs{ p}\) representar a\(\vecs{ v}\) projeção de em\(\vecs{ u}\):

\[ \begin{align*} \vecs{ p} &=\text{proj}_\vecs{ u}\vecs{ v} \\[4pt] &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{⟨2,3,2⟩⋅⟨8,−3,−3⟩}{∥⟨2,3,2⟩∥^2}⟨2,3,2⟩ \\[4pt] &=\dfrac{16−9−6}{2^2+3^2+2^2}⟨2,3,2⟩ \\[4pt] &=\dfrac{1}{17}⟨2,3,2⟩ \\[4pt] &=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩. \end{align*} \nonumber \]

Em seguida,

\[ \begin{align*} \vecs{ q} &=\vecs{ v}−\vecs{ p}=⟨8,−3,−3⟩−⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩\\[4pt] &=⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩. \end{align*} \nonumber \]

Para verificar nosso trabalho, podemos usar o produto escalar para verificar se\(\vecs{ p}\)\(\vecs{ q}\) são vetores ortogonais:

\[ \begin{align*}\vecs{ p}⋅\vecs{ q}&=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩⋅⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩\\[4pt] &=\dfrac{268}{289}−\dfrac{162}{289}−\dfrac{106}{289}=0. \end{align*} \nonumber \]

Em seguida,

\[\vecs{ v}=\vecs{ p}+\vecs{ q}=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩+⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩. \nonumber \]

Exercício\(\PageIndex{7}\)

\(\vecs{ v}=5\mathbf{\hat i}−\mathbf{\hat j}\)Expresse como uma soma de vetores ortogonais de forma que um dos vetores tenha a mesma direção que\(\vecs{ u}=4\mathbf{\hat i}+2\mathbf{\hat j}\).

Dica

Comece encontrando a projeção de\(\vecs{ v}\) em cima\(\vecs{ u}\).

Responda

\(\vecs{ v}=\vecs{ p}+\vecs{ q},\)onde\(\vecs{ p}=\dfrac{18}{5}\mathbf{\hat i}+\dfrac{9}{5}\mathbf{\hat j}\) e\(\vecs{ q}=\dfrac{7}{5}\mathbf{\hat i}−\dfrac{14}{5}\mathbf{\hat j}\)

Exemplo\(\PageIndex{9}\): Scalar Projection of Velocity

Um navio porta-contêineres deixa o porto viajando\(15°\) ao norte do leste. Seu motor gera uma velocidade de 20 nós ao longo desse caminho (veja a figura a seguir). Além disso, a corrente oceânica move o navio para o nordeste a uma velocidade de 2 nós. Considerando tanto o motor quanto a corrente, com que rapidez o navio está se movendo na direção\(15°\) norte ou leste? Arredonde a resposta para duas casas decimais.

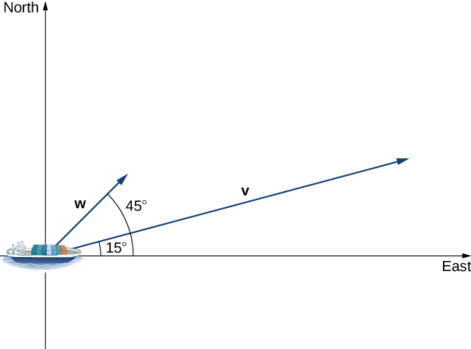
Solução

\(\vecs{ v}\)Seja o vetor de velocidade gerado pelo motor e\(\vecs{w}\) seja o vetor de velocidade da corrente. Já conhecemos a\(‖\vecs{ v}‖=20\) rota desejada. Só precisamos adicionar a projeção escalar de\(\vecs{ w}\) onto\(\vecs{ v}\). Nós recebemos

\[ \begin{align*} \text{comp}_\vecs{ v}\vecs{ w}=\dfrac{\vecs{ v}⋅\vecs{ w}}{‖\vecs{ v}‖} \\[4pt] =\dfrac{‖\vecs{ v}‖‖\vecs{ w}‖\cos(30°)}{‖\vecs{ v}‖} =‖\vecs{ w}‖\cos(30°) =2\dfrac{\sqrt{3}}{2}=\sqrt{3}≈1.73\,\text{knots.}\end{align*}\]

O navio está se movendo a 21,73 nós na direção\(15°\) norte do leste.

Exercício\(\PageIndex{8}\)

Repita o exemplo anterior, mas suponha que a corrente oceânica esteja se movendo para sudeste em vez de nordeste, conforme mostrado na figura a seguir.

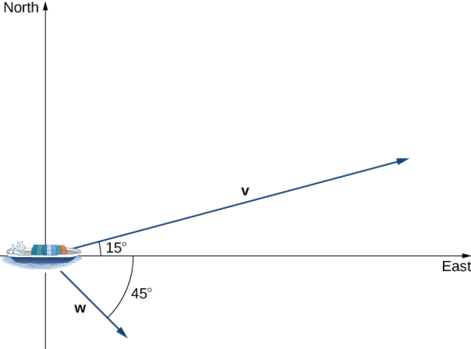
Dica

Calcule a projeção escalar de\(\vecs{ w}\) em cima\(\vecs{ v}\).

Responda

21 nós

Trabalhar

Agora que entendemos os produtos com pontos, podemos ver como aplicá-los a situações da vida real. A aplicação mais comum do produto escalar de dois vetores é no cálculo do trabalho.

Pela física, sabemos que o trabalho é feito quando um objeto é movido por uma força. Quando a força é constante e aplicada na mesma direção em que o objeto se move, definimos o trabalho realizado como o produto da força e da distância que o objeto percorre:\(W=Fd\). Vimos vários exemplos desse tipo em capítulos anteriores. Agora imagine que a direção da força é diferente da direção do movimento, como no exemplo de uma criança puxando uma carroça. Para encontrar o trabalho realizado, precisamos multiplicar o componente da força que atua na direção do movimento pela magnitude do deslocamento. O produto escalar nos permite fazer exatamente isso. Se representarmos uma força aplicada por um vetor\(\vecs{ F}\) e o deslocamento de um objeto por um vetor\(\vecs{ s}\), então o trabalho realizado pela força é o produto escalar de\(\vecs{ F}\)\(\vecs{ s}\) e.

Definição: Força constante

Quando uma força constante é aplicada a um objeto para que o objeto se mova em linha reta de um ponto\(P\) a outro\(Q\), o trabalho\(W\) realizado pela força\(\vecs{ F}\), atuando em um ângulo θ da linha de movimento, é dado por

\[W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ. \nonumber \]

Vamos revisitar o problema do vagão infantil apresentado anteriormente. Suponha que uma criança esteja puxando um vagão com uma força de magnitude de 8 lb na alça em um ângulo de 55°. Se a criança puxar o vagão de 50 pés, encontre o trabalho realizado pela força (Figura\(\PageIndex{8}\)).

Figura\(\PageIndex{8}\): O componente horizontal da força é a\(\vecs{ F}\) projeção de no\(x\) eixo positivo.

Nós temos

\[W=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ=8(50)(\cos(55°))≈229\,\text{ft⋅lb.} \nonumber \]

Nas unidades padrão dos EUA, medimos a magnitude da força\(∥\vecs{ F}∥\) em libras. A magnitude do vetor de deslocamento nos\(∥\vecd{PQ}∥\) diz até onde o objeto se moveu e é medido em pés. A unidade de medida habitual para o trabalho, então, é o pé-libra. Um pé de libra é a quantidade de trabalho necessária para mover um objeto pesando 1 lb a uma distância de 1 pé em linha reta. No sistema métrico, a unidade de medida da força é o newton (N) e a unidade de medida da magnitude do trabalho é um newton-metro (N·m) ou um joule (J).

Exemplo\(\PageIndex{10}\): Calculating Work

Uma correia transportadora gera uma força\(\vecs{ F}=5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k}\) que move uma mala de um ponto\((1,1,1)\) a outro ao\((9,4,7)\) longo de uma linha reta. Encontre o trabalho realizado pela correia transportadora. A distância é medida em metros e a força é medida em newtons.

Solução

O vetor de deslocamento\(\vecd{PQ}\) tem ponto inicial\((1,1,1)\) e ponto terminal\((9,4,7)\):

\[\vecd{PQ}=⟨9−1,4−1,7−1⟩=⟨8,3,6⟩=8\mathbf{\hat i}+3\mathbf{\hat j}+6\mathbf{\hat k}. \nonumber \]

O trabalho é o produto escalar da força e do deslocamento:

\[\begin{align*} W &=\vecs{ F}⋅\vecd{PQ} \\[4pt] &= (5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k})⋅(8\mathbf{\hat i}+3\mathbf{\hat j}+6\mathbf{\hat k}) \\[4pt] = 5(8)+(−3)(3)+1(6) \\[4pt] &=37\,\text{N⋅m} \\[4pt] &= 37\,\text{J} \end{align*}\]

Exercício\(\PageIndex{9}\)

Uma força constante de 30 lb é aplicada em um ângulo de 60° para puxar um carrinho de mão de 10 pés pelo chão. Qual é o trabalho realizado por essa força?

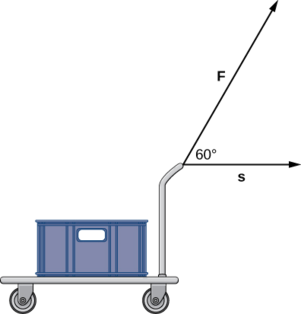
Dica

Use a definição de trabalho como o produto escalar da força e da distância.

Responda

150 pés-lb

Conceitos-chave

• O produto escalar, ou produto escalar, de dois vetores\(\vecs{ u}=⟨u_1,u_2,u_3⟩\) e\(\vecs{ v}=⟨v_1,v_2,v_3⟩\) é\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3\).
• O produto escalar satisfaz as seguintes propriedades:
  • \(\vecs{ u}⋅\vecs{ v}=\vecs{ v}⋅\vecs{ u}\)
  • \(\vecs{ u}⋅(\vecs{ v}+\vecs{ w})=\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ w}\)
  • \(c(\vecs{ u}⋅\vecs{ v})=(c\vecs{ u})⋅\vecs{ v}=\vecs{ u}⋅(c\vecs{ v})\)
  • \(\vecs{ v}⋅\vecs{ v}=‖\vecs{ v}‖^2\)
• O produto escalar de dois vetores pode ser expresso, alternativamente, como\(\vecs{ u}⋅\vecs{ v}=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ.\) Esta forma do produto escalar é útil para encontrar a medida do ângulo formado por dois vetores.
• Vetores\(\vecs{ u}\) e\(\vecs{ v}\) são ortogonais se\(\vecs{ u}⋅\vecs{ v}=0\).
• Os ângulos formados por um vetor diferente de zero e os eixos coordenados são chamados de ângulos de direção do vetor. Os cossenos desses ângulos são conhecidos como cossenos de direção.
• A projeção vetorial de\(\vecs{ v}\) onto\(\vecs{ u}\) é o vetor\(\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}\). A magnitude desse vetor é conhecida como projeção escalar de\(\vecs{ v}\) onto\(\vecs{ u}\), dada por\(\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\).
• O trabalho é feito quando uma força é aplicada a um objeto, causando deslocamento. Quando a força é representada pelo vetor\(\vecs{ F}\) e o deslocamento é representado pelo vetor\(\vecs{ s}\), o trabalho realizado\(W\) é dado pela fórmula\(W=\vecs{ F}⋅\vecs{ s}=∥\vecs{ F}∥‖\vecs{ s}‖\cos θ.\)

Equações-chave

• Produto escalar de\(\vecs{ u}\) e\(\vecs{ v}\)

\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ\)

• Cosseno do ângulo formado por\(\vecs{ u}\) e\(\vecs{ v}\)

\(\cos θ=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}\)

• Projeção vetorial de\(\vecs{ v}\) em\(\vecs{ u}\)

\(\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}\)

• Projeção escalar de\(\vecs{ v}\) onto\(\vecs{ u}\)

\(\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\)

• Trabalho realizado por uma força\(\vecs{ F}\) para mover um objeto através do vetor de deslocamento\(\vecd{PQ}\)

\(W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ\)

Glossário

ângulos de direção

os ângulos formados por um vetor diferente de zero e os eixos coordenados

cossenos de direção

os cossenos dos ângulos formados por um vetor diferente de zero e os eixos coordenados

produto escalar ou produto escalar

\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3\)onde\(\vecs{ u}=⟨u_1,u_2,u_3⟩\) e\(\vecs{ v}=⟨v_1,v_2,v_3⟩\)

projeção escalar

a magnitude da projeção vetorial de um vetor

vetores ortogonais

vetores que formam um ângulo reto quando colocados na posição padrão

projeção vetorial

o componente de um vetor que segue uma determinada direção

trabalho realizado por uma força

o trabalho é geralmente considerado como a quantidade de energia necessária para mover um objeto; se representarmos uma força aplicada por um vetor\(\vecs{ F}\) e o deslocamento de um objeto por um vetor\(\vecs{ s}\), então o trabalho realizado pela força é o produto escalar de\(\vecs{ F}\)\(\vecs{ s}\) e.

Contribuidores e atribuições

• Template:ContribOpenStaxCalc
• edited for vector notation by Paul Seeburger