4.11: Exercícios de revisão do capítulo 4

Last updated
Save as PDF

Page ID: 188254

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Verdadeiro ou falso? Justifique sua resposta com uma prova ou um contra-exemplo. Suponha que$f(x)$ seja contínuo e diferenciável, salvo indicação em contrário.

1) Se$f(−1)=−6$ e$f(1)=2$, então existe pelo menos um ponto$x∈[−1,1]$ tal que$f′(x)=4.$

Responda: Verdadeiro, pelo Teorema do Valor Médio

2) Se$f′(c)=0,$ houver um máximo ou mínimo em$x=c.$

3) Existe uma função tal que$f(x)<0,f′(x)>0,$ e$f''(x)<0.$ (Uma “prova” gráfica é aceitável para essa resposta.)

Responda: É verdade

4) Existe uma função tal que existe um ponto de inflexão e um ponto crítico para algum valor$x=a.$

5) Dado o gráfico de$f′$, determine onde$f$ está aumentando ou diminuindo.

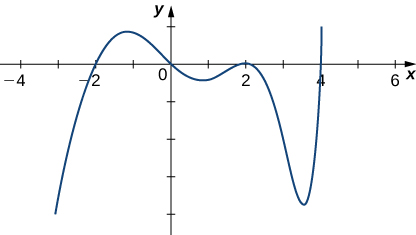
$A função aumenta para cruzar o eixo x em −2, atinge um máximo e depois diminui através da origem, atinge um mínimo e depois aumenta para um máximo em 2, diminui para um mínimo e depois aumenta para passar pelo eixo x em 4 e continua aumentando.$

Responda: Aumentando:$(−2,0)∪(4,∞)$, diminuindo:$(−∞,−2)∪(0,4)$

6) O gráfico de$f$ é fornecido abaixo. Desenhe$f′$.

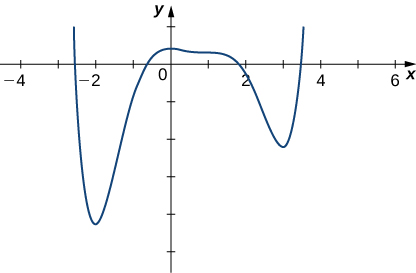
$A função diminui rapidamente e atinge um mínimo local em −2, depois aumenta para atingir um máximo local em 0, momento em que ela diminui lentamente no início, depois para de diminuir perto de 1, depois continua diminuindo até atingir um mínimo em 3 e depois aumenta rapidamente.$

7) Encontre a aproximação linear$y=x^2+\tan(πx)$ de$L(x)$ perto$x=\frac{1}{4}.$

Responda: $L(x)=\frac{17}{16}+\frac{1}{2}(1+4π)\left(x−\frac{1}{4}\right)$

8) Encontre o diferencial$y=x^2−5x−6$ e avalie$x=2$ com$dx=0.1.$

Encontre os pontos críticos e os extremos locais e absolutos das seguintes funções em um determinado intervalo.

9)$f(x)=x+\sin^2(x)$ acabou$[0,π]$

Responda: Ponto crítico: mínimo$x=\frac{3π}{4},$
absoluto:$0$ quando Máximo$x=0,$
absoluto:$π$ quando$x=π$

Solução:

10)$f(x)=3x^4−4x^3−12x^2+6$ acabou$[−3,3]$

Determine em quais intervalos as seguintes funções estão aumentando, diminuindo, côncavas para cima e côncavas para baixo.

11)$x(t)=3t^4−8t^3−18t^2$

Responda: Aumentando:$(−1,0)∪(3,∞),$
Decrescente:$(−∞,−1)∪(0,3),$
côncavo para cima:$\left(−∞,\frac{1}{3}\left(2−\sqrt{13}\right)\right)∪\left(\frac{1}{3}\left(2+\sqrt{13}\right),∞\right)$,
Côncavo para baixo:$\left(\frac{1}{3}\left(2−\sqrt{13}\right),\frac{1}{3}\left(2+\sqrt{13}\right)\right)$

12)$y=x+\sin(πx)$

13)$g(x)=x−\sqrt{x}$

Responda: Aumentando:$\left(\frac{1}{4},∞\right),$
Diminuindo:$\left(0,\frac{1}{4}\right)$,
Côncavo para cima:$(0,∞),$
Côncavo para baixo: nenhum

14)$f(θ)=\sin(3θ)$

Avalie os seguintes limites.

15)$\displaystyle \lim_{x→∞}\frac{3x\sqrt{x^2+1}}{\sqrt{x^4−1}}$

Responda: $3$

16)$\displaystyle \lim_{x→∞}\cos\left(\frac{1}{x}\right)$

17)$\displaystyle \lim_{x→1}\frac{x−1}{\sin(πx)}$

Responda: $−\frac{1}{π}$

18)$\displaystyle \lim_{x→∞}(3x)^{1/x}$

Use o método de Newton para encontrar as duas primeiras iterações, dado o ponto de partida.

19)$y=x^3+1,\quad x_0=0.5$

Responda: $x_1=−1,\; x_2=−1$

20)$\dfrac{1}{x+1}=\dfrac{1}{2}, \quad x_0=0$

Encontre as antiderivadas$F(x)$ das seguintes funções.

21)$g(x)=\sqrt{x}−\dfrac{1}{x^2}$

Responda: $F(x)=\dfrac{2x^{3/2}}{3}+\dfrac{1}{x}+C$

22)$f(x)=2x+6\cos x,\quad F(π)=π^2+2$

Faça um gráfico manual das seguintes funções. Certifique-se de rotular os pontos de inflexão, pontos críticos, zeros e assíntotas.

23)$y=\dfrac{1}{x(x+1)^2}$

Responda

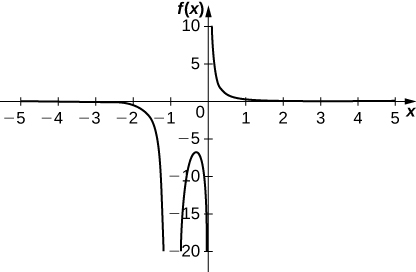
$Este gráfico tem assíntotas verticais em x = 0 e x = −1. A primeira parte da função ocorre no terceiro quadrante com uma assíntota horizontal em y = 0. A função diminui rapidamente de perto (−5, 0) para perto da assíntota vertical (−1, ∞). No outro lado da assíntota, a função é aproximadamente em forma de U e apontada para baixo no terceiro quadrante entre x = −1 e x = 0 com o máximo próximo (−0,4, −6). Do outro lado da assíntota x = 0, a função diminui de sua assíntota vertical próxima (0, ∞) para se aproximar da assíntota horizontal y = 0.$

Pontos de inflexão: nenhum; Pontos
críticos:$x=−\frac{1}{3}$;
Zeros: nenhum; Assíntotas
verticais:$x=−1, \; x=0$; Assíntota
horizontal:$y=0$

24)$y=x−\sqrt{4−x^2}$

25) Um carro está sendo compactado em um sólido retangular. O volume está diminuindo a uma taxa de$2\, \text{m}^3/\text{sec}$. O comprimento e a largura do compactador são quadrados, mas a altura não é o mesmo comprimento que o comprimento e a largura. Se as paredes de comprimento e largura se moverem uma em direção à outra a uma taxa de$0.25$ m/seg, encontre a taxa na qual a altura está mudando quando o comprimento e a largura são$2$ m e a altura é$1.5$ m.

Responda: A altura está diminuindo a uma taxa de$0.125$ m/seg

26) Um foguete é lançado ao espaço; sua energia cinética é dada por$K(t)=\frac{1}{2}m(t)v(t)^2$, onde$K$ está a energia cinética em joules,$m$ é a massa do foguete em quilogramas e$v$ é a velocidade do foguete em metros/segundo. Suponha que a velocidade esteja aumentando a uma taxa de$15 \,\text{m/sec}^2$ e a massa esteja diminuindo a uma taxa de$10$ kg/seg porque o combustível está sendo queimado. A que velocidade a energia cinética do foguete muda quando a massa é$2000$ kg e a velocidade é$5000$ m/seg? Dê sua resposta em Mega-joules (MJ), o que equivale a$10^6$ J.

27) O famoso problema de Regiomontanus para a maximização do ângulo foi proposto durante o$15^\text{th}$ século. Uma pintura está pendurada em uma parede com a parte inferior da pintura a uma distância de$a$ pés acima do nível dos olhos e os$b$ pés superiores acima do nível dos olhos. A que distância$x$ (em pés) da parede o espectador deve ficar para maximizar o ângulo subtendido pela pintura$θ$?

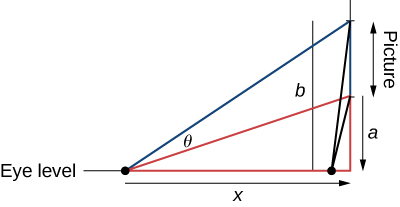
$Um ponto é marcado no nível dos olhos e, a partir desse ponto, um triângulo reto é feito com o comprimento do lado adjacente x e o comprimento do lado oposto a, que é o comprimento da parte inferior da imagem até o nível do olho. Um segundo triângulo reto é feito a partir do ponto marcado no nível dos olhos, com o lado adjacente sendo x e o outro lado sendo o comprimento b, que é a altura da imagem. O ângulo entre as duas hipotenusas está marcado como θ.$

Responda: $x=\sqrt{ab}$pés

28) Uma companhia aérea vende passagens de Tóquio para Detroit porque$$1200.$ há$500$ assentos disponíveis e um voo típico reserva$350$ assentos. Para cada$$10$ queda no preço, a companhia aérea observa mais cinco assentos vendidos. Qual deve ser a tarifa para maximizar o lucro? Quantos passageiros estariam a bordo?