10.6: Calculando momentos de inércia

objetivos de aprendizagem

• Calcule o momento de inércia para corpos rígidos de formato uniforme
• Aplique o teorema do eixo paralelo para encontrar o momento de inércia sobre qualquer eixo paralelo a um já conhecido
• Calcule o momento de inércia para objetos compostos

Na subseção anterior, definimos o momento de inércia, mas não mostramos como calculá-lo. Nesta subseção, mostramos como calcular o momento de inércia para vários tipos padrão de objetos, bem como usar momentos de inércia conhecidos para encontrar o momento de inércia de um eixo deslocado ou de um objeto composto. Esta seção é muito útil para ver como aplicar uma equação geral a objetos complexos (uma habilidade essencial para cursos mais avançados de física e engenharia).

Momento de inércia

Definimos o momento de inércia I de um objeto a ser

\[I = \sum_{i} m_i r_i^2 \]

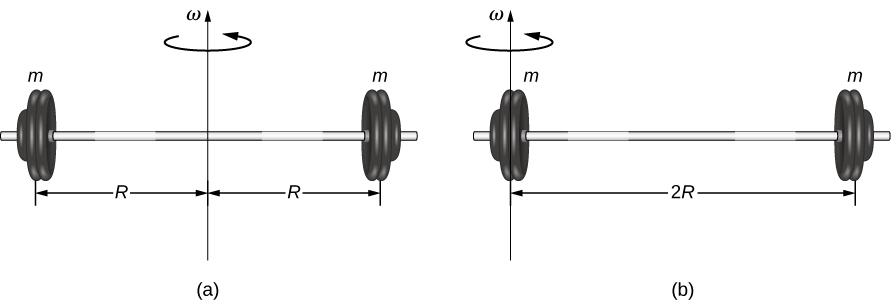
para todas as massas de pontos que compõem o objeto. Como\(r\) é a distância até o eixo de rotação de cada pedaço de massa que compõe o objeto, o momento de inércia de qualquer objeto depende do eixo escolhido. Para ver isso, vamos pegar um exemplo simples de duas massas no final de uma haste sem massa (massa insignificantemente pequena) (Figura\(\PageIndex{1}\)) e calcular o momento de inércia em torno de dois eixos diferentes. Nesse caso, a soma das massas é simples porque as duas massas no final da barra podem ser aproximadas como massas pontuais e, portanto, a soma tem apenas dois termos.

No caso do eixo no centro da barra, cada uma das duas massas m está a uma\(R\) distância do eixo, dando um momento de inércia de

\[I_{1} = mR^{2} + mR^{2} = 2mR^{2} \ldotp\]

No caso do eixo no final da barra — passando por uma das massas — o momento de inércia é

\[I_{2} = m(0)^{2} + m(2R)^{2} = 4mR^{2} \ldotp\]

A partir desse resultado, podemos concluir que é duas vezes mais difícil girar a barra em torno da extremidade do que em torno do centro.

Figura\(\PageIndex{1}\): (a) Uma barra com um eixo de rotação em seu centro; (b) uma barra com um eixo de rotação em uma extremidade.

Neste exemplo, tínhamos duas massas de pontos e a soma era simples de calcular. No entanto, para lidar com objetos que não são pontuais, precisamos pensar cuidadosamente sobre cada um dos termos da equação. A equação pede que somemos sobre cada “peça de massa” uma certa distância do eixo de rotação. Mas o que exatamente significa cada “pedaço de massa”? Lembre-se de que em nossa derivação dessa equação, cada peça de massa tinha a mesma magnitude de velocidade, o que significa que a peça inteira tinha que ter uma única distância r até o eixo de rotação. No entanto, isso não é possível, a menos que peguemos um pedaço de massa dm infinitesimalmente pequeno, conforme mostrado na Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Usando um pedaço de massa infinitesimalmente pequeno para calcular a contribuição para o momento total de inércia.

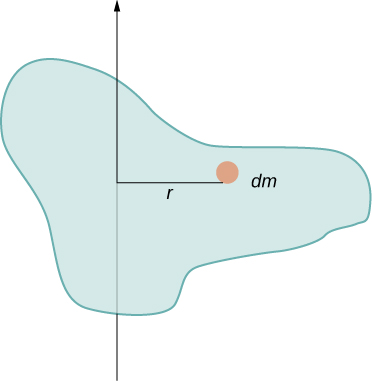
A necessidade de usar um pedaço de massa infinitesimalmente pequeno dm sugere que podemos escrever o momento de inércia avaliando uma integral sobre massas infinitesimais em vez de fazer uma soma discreta sobre massas finitas:

\[I = \sum_{i} m_{i} r_{i}^{2}\]

torna-se

\[I = \int r^{2} dm \ldotp \label{10.19}\]

Essa, na verdade, é a forma que precisamos para generalizar a equação para formas complexas. É melhor elaborar exemplos específicos em detalhes para ter uma ideia de como calcular o momento de inércia para formas específicas. Esse é o foco da maior parte do restante desta seção.

Uma haste fina uniforme com um eixo no centro

Considere uma haste fina uniforme (densidade e forma) de massa M e comprimento L, conforme mostrado na Figura\(\PageIndex{3}\). Queremos uma haste fina para que possamos assumir que a área da seção transversal da haste é pequena e que a haste pode ser considerada como uma série de massas ao longo de uma linha reta unidimensional. Neste exemplo, o eixo de rotação é perpendicular à haste e passa pelo ponto médio para simplificar. Nossa tarefa é calcular o momento de inércia sobre esse eixo. Orientamos os eixos para que o eixo z seja o eixo de rotação e o eixo x passe pelo comprimento da haste, conforme mostrado na figura. Essa é uma escolha conveniente porque podemos então integrar ao longo do eixo x.

Figura\(\PageIndex{3}\): Cálculo do momento de inércia I para uma haste fina uniforme em torno de um eixo que passa pelo centro da haste.

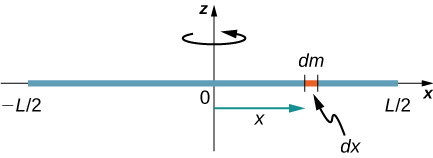
Definimos dm como um pequeno elemento de massa que compõe a haste. A integral do momento de inércia é uma integral sobre a distribuição de massa. No entanto, sabemos como nos integrar sobre o espaço, não sobre a massa. Portanto, precisamos encontrar uma maneira de relacionar massa com variáveis espaciais. Fazemos isso usando a densidade\(\lambda\) de massa linear do objeto, que é a massa por unidade de comprimento. Como a densidade de massa desse objeto é uniforme, podemos escrever

\[\lambda = \frac{m}{l}\; or\; m = \lambda l \ldotp\]

Se tomarmos o diferencial de cada lado dessa equação, encontramos

\[dm = d(\lambda l) = \lambda (dl)\]

já que\(\lambda\) é constante. Optamos por orientar a haste ao longo do eixo x por conveniência — é aqui que essa escolha se torna muito útil. Observe que um pedaço da haste dl fica completamente ao longo do eixo x e tem um comprimento dx; na verdade, dl = dx nessa situação. Portanto, podemos escrever dm =\(\lambda\) (dx), fornecendo uma variável de integração com a qual sabemos como lidar. A distância de cada peça de massa dm do eixo é dada pela variável x, conforme mostrado na figura. Juntando tudo isso, obtemos

\[I = \int r^{2} dm = \int x^{2} dm = \int x^{2} \lambda dx \ldotp\]

O último passo é ter cuidado com nossos limites de integração. A haste se estende de x =\(− \frac{L}{2}\) a x =\(\frac{L}{2}\), já que o eixo está no meio da haste em x = 0. Isso nos dá

\[\begin{split} I & = \int_{- \frac{L}{2}}^{\frac{L}{2}} x^{2} \lambda dx = \lambda \frac{x^{3}}{3} \Bigg|_{- \frac{L}{2}}^{\frac{L}{2}} \\ & = \lambda \left(\dfrac{1}{3}\right) \Bigg[ \left(\dfrac{L}{2}\right)^{3} - \left(- \dfrac{L}{2}\right)^{3} \Bigg] = \lambda \left(\dfrac{1}{3}\right) \left(\dfrac{L^{3}}{8}\right) (2) = \left(\dfrac{M}{L}\right) \left(\dfrac{1}{3}\right) \left(\dfrac{L^{3}}{8}\right) (2) \\ & = \frac{1}{12} ML^{2} \ldotp \end{split}\]

Em seguida, calculamos o momento de inércia para a mesma haste fina uniforme, mas com uma escolha de eixo diferente para que possamos comparar os resultados. Esperaríamos que o momento de inércia fosse menor em torno de um eixo que passa pelo centro de massa do que o eixo do ponto final, assim como foi para o exemplo da barra no início desta seção. Isso acontece porque mais massa é distribuída mais longe do eixo de rotação.

Uma haste fina uniforme com eixo na extremidade

Agora, considere a mesma haste fina uniforme de massa\(M\) e comprimento\(L\), mas desta vez movemos o eixo de rotação até o final da haste. Queremos encontrar o momento de inércia sobre esse novo eixo (Figura\(\PageIndex{4}\)).

Figura\(\PageIndex{4}\): Cálculo do momento de inércia\(I\) para uma haste fina uniforme em torno de um eixo que passa pela extremidade da haste.

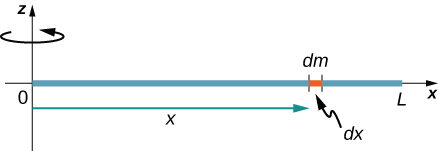
A quantidade\(dm\) é novamente definida como sendo um pequeno elemento de massa que compõe a haste. Assim como antes, obtemos

\[I = \int r^{2} dm = \int x^{2} dm = \int x^{2} \lambda dx \ldotp\]

No entanto, desta vez, temos diferentes limites de integração. A haste se estende de\(x = 0\) até\(x = L\), já que o eixo está na extremidade da haste em\(x = 0\). Portanto, encontramos

\[\begin{align} I & = \int_{0}^{L} x^{2} \lambda\, dx \\[4pt] &= \lambda \frac{x^{3}}{3} \Bigg|_{0}^{L} \\[4pt] &=\lambda \left(\dfrac{1}{3}\right) \Big[(L)^{3} - (0)^{3} \Big] \\[4pt] & = \lambda \left(\dfrac{1}{3}\right) L^{3} = \left(\dfrac{M}{L}\right) \left(\dfrac{1}{3}\right) L^{3} \\[4pt] &= \frac{1}{3} ML^{2} \ldotp \label{ThinRod} \end{align} \]

Observe que a inércia rotacional da haste em torno de sua extremidade é maior do que a inércia rotacional em torno de seu centro (consistente com o exemplo da barra) por um fator de quatro.

O Teorema do Eixo Paralelo

A semelhança entre o processo de encontrar o momento de inércia de uma haste em torno de um eixo no meio e cerca de um eixo na extremidade é impressionante, e sugere que pode haver um método mais simples para determinar o momento de inércia de uma haste sobre qualquer eixo paralelo ao eixo através do centro de massa. Esse eixo é chamado de eixo paralelo. Existe um teorema para isso, chamado teorema do eixo paralelo, que afirmamos aqui, mas não derivamos neste texto.

Teorema do eixo paralelo

Seja m a massa de um objeto e seja d a distância de um eixo através do centro de massa do objeto até um novo eixo. Então nós temos

\[I_{\text{parallel-axis}} = I_{\text{center of mass}} + md^{2} \ldotp \label{10.20}\]

Vamos aplicar isso à haste fina uniforme com o exemplo de eixo resolvido acima:

\[I_{parallel-axis} = I_{center\; of\; mass} + md^{2} = \frac{1}{12} mL^{2} + m \left(\dfrac{L}{2}\right)^{2} = \left(\dfrac{1}{12} + \dfrac{1}{4}\right) mL^{2} = \frac{1}{3} mL^{2} \ldotp\]

Esse resultado concorda com nosso cálculo mais longo (Equation\ ref {thinRod}). A equação\ ref {10.20} é uma equação útil que aplicamos em alguns dos exemplos e problemas.

Exercício\(\PageIndex{1}\)

Qual é o momento de inércia de um cilindro de raio\(R\) e massa em\(m\) torno de um eixo através de um ponto na superfície, conforme mostrado abaixo?

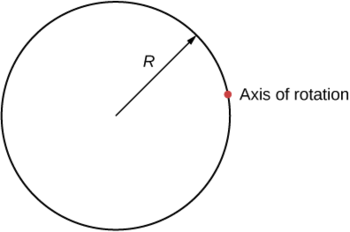
Responda

\[I_{parallel-axis} = I_{center\; of\; mass} + md^{2} = mR^{2} + mR^{2} = 2mR^{2} \nonumber \]

Um disco fino uniforme em torno de um eixo que passa pelo centro

A integração para encontrar o momento de inércia de um objeto bidimensional é um pouco mais complicada, mas uma forma geralmente é feita nesse nível de estudo - um disco fino uniforme em torno de um eixo através de seu centro (Figura\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\): Calculando o momento de inércia de um disco fino em torno de um eixo através de seu centro.

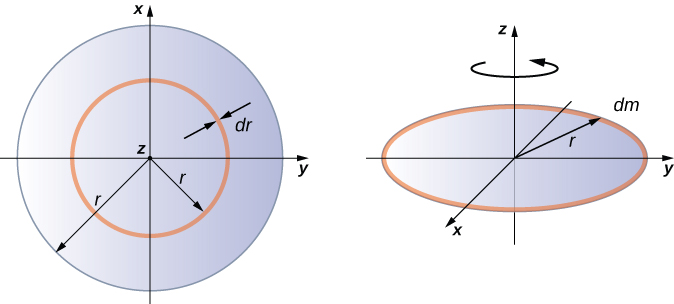
Como o disco é fino, podemos considerar a massa totalmente distribuída no plano xy. Começamos novamente com a relação para a densidade de massa superficial, que é a massa por unidade de área de superfície. Por ser uniforme, a densidade da massa superficial\(\sigma\) é constante:

\[\sigma = \frac{m}{A}\]ou\[\sigma A = m\] então\[dm = \sigma (dA)\]

Agora usamos uma simplificação para a área. A área pode ser considerada composta por uma série de anéis finos, onde cada anel é um incremento de massa dm de raio\(r\) equidistante do eixo, conforme mostrado na parte (b) da figura. A área infinitesimal de cada anel\(dA\) é, portanto, dada pelo comprimento de cada anel (\(2 \pi r\)) vezes a largura infinitesimal de cada anel\(dr\):

\[A = \pi r^{2},\; dA = d(\pi r^{2}) = \pi dr^{2} = 2 \pi rdr \ldotp\]

A área total do disco é então composta pela adição de todos os anéis finos com um raio\(0\) que varia de\(R\) a. Essa faixa de raio então se torna nosso limite de integração\(dr\), ou seja, integramos de\(r = 0\) para\(r = R\). Juntando tudo isso, temos

\[\begin{split} I & = \int_{0}^{R} r^{2} \sigma (2 \pi r) dr = 2 \pi \sigma \int_{0}^{R} r^{3} dr = 2 \pi \sigma \frac{r^{4}}{4} \Big|_{0}^{R} \\ & = 2 \pi \sigma \left(\dfrac{R^{4}}{4} - 0 \right) = 2 \pi \left(\dfrac{m}{A}\right) \left(\dfrac{R^{4}}{4}\right) = 2 \pi \left(\dfrac{m}{\pi R^{2}}\right) \left(\dfrac{R^{4}}{4}\right) = \frac{1}{2} mR^{2} \ldotp \end{split}\]

Observe que isso concorda com o valor dado na Figura 10.5.4.

Calculando o momento de inércia para objetos compostos

Agora, considere um objeto composto como o da Figura\(\PageIndex{6}\), que mostra um disco fino na extremidade de uma haste fina. Isso não pode ser facilmente integrado para encontrar o momento de inércia porque não é um objeto de formato uniforme. No entanto, se voltarmos à definição inicial de momento de inércia como soma, podemos argumentar que o momento de inércia de um objeto composto pode ser encontrado a partir da soma de cada parte do objeto:

\[I_{total} = \sum_{i} I_{i} \ldotp \label{10.21}\]

É importante observar que os momentos de inércia dos objetos na Equação\(\PageIndex{6}\) são sobre um eixo comum. No caso desse objeto, isso seria uma haste de comprimento L girando em torno de sua extremidade, e um fino disco de raio\(R\) girando em torno de um eixo deslocado para fora do centro por uma distância\(L + R\), onde\(R\) está o raio do disco. Vamos definir a massa da haste como m _r e a massa do disco como sendo\(m_d\).

Figura\(\PageIndex{6}\): Objeto composto que consiste em um disco na extremidade de uma haste. O eixo de rotação está localizado em\(A\).

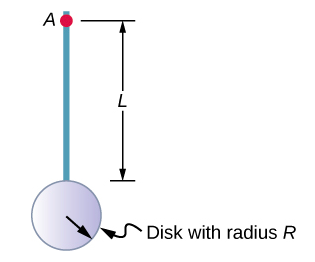
O momento de inércia da haste é simples\(\frac{1}{3} m_rL^2\), mas temos que usar o teorema do eixo paralelo para encontrar o momento de inércia do disco em torno do eixo mostrado. O momento de inércia do disco em torno de seu centro é\(\frac{1}{2} m_dR^2\) e aplicamos o teorema do eixo paralelo (Equação\ ref {10.20}) para encontrar

\[I_{parallel-axis} = \frac{1}{2} m_{d} R^{2} + m_{d} (L + R)^{2} \ldotp\]

Somando o momento de inércia da haste mais o momento de inércia do disco com um eixo de rotação deslocado, descobrimos que o momento de inércia do objeto composto é

\[I_{total} = \frac{1}{3} m_{r} L^{2} + \frac{1}{2} m_{d} R^{2} + m_{d} (L + R)^{2} \ldotp\]

Aplicação de cálculos de momento de inércia para resolver problemas

Agora vamos examinar algumas aplicações práticas dos cálculos do momento de inércia.

Exemplo\(\PageIndex{1}\): Person on a Merry-Go-Round

Uma criança de 25 kg fica a uma\(r = 1.0\, m\) distância do eixo de um carrossel giratório (Figura\(\PageIndex{7}\)). O carrossel pode ser aproximado como um disco sólido uniforme com uma massa de 500 kg e um raio de 2,0 m. Encontre o momento de inércia desse sistema.

Figura\(\PageIndex{7}\): Calculando o momento de inércia de uma criança em um carrossel.

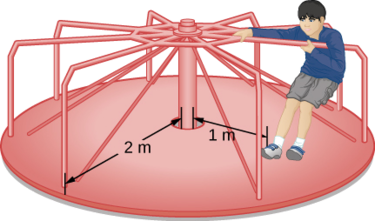
Estratégia

Esse problema envolve o cálculo de um momento de inércia. Recebemos a massa e a distância até o eixo de rotação da criança, bem como a massa e o raio do carrossel. Como a massa e o tamanho da criança são muito menores do que o carrossel, podemos aproximar a criança como uma massa pontual. A notação que usamos é m _c = 25 kg, r _c = 1,0 m, _{m m} = 500 kg, r _m = 2,0 m. Nosso objetivo é encontrar\(I_{total} = \sum_{i} I_{i}\) (Equação\ ref {10.21}).

Solução

Para a criança\(I_c = m_cr^2\), e para o carrossel,\(I_m = \frac{1}{2}m_m r^2\). Portanto

\[I_{total} = 25(1)^{2} + \frac{1}{2} (500)(2)^{2} = 25 + 1000 = 1025\; kg\; \cdotp m^{2} \ldotp \nonumber \]

Significância

O valor deve estar próximo ao momento de inércia do carrossel por si só, pois ele tem muito mais massa distribuída para longe do eixo do que a criança.

Exemplo\(\PageIndex{2}\): Rod and Solid Sphere

Encontre o momento de inércia da combinação de haste e esfera sólida em torno dos dois eixos, conforme mostrado abaixo. A haste tem comprimento de 0,5 m e massa de 2,0 kg. O raio da esfera é de 20,0 cm e tem massa de 1,0 kg.

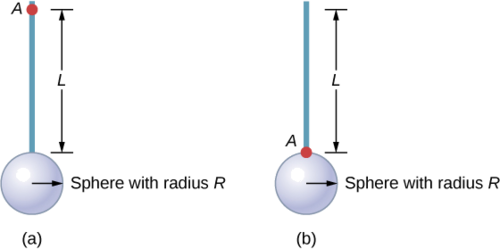
Estratégia

Como temos um objeto composto em ambos os casos, podemos usar o teorema do eixo paralelo para encontrar o momento de inércia sobre cada eixo. Em (a), o centro de massa da esfera está localizado a uma\(L + R\) distância do eixo de rotação. Em (b), o centro de massa da esfera está localizado a uma\(R\) distância do eixo de rotação. Em ambos os casos, o momento de inércia da haste é cerca de um eixo em uma extremidade. Consulte a Tabela 10.4 para ver os momentos de inércia dos objetos individuais.

uma.

\[\begin{split} I_{total} & = \sum_{i} I_{i} = I_{Rod} + I_{Sphere}; \\ I_{Sphere} & = I_{center\; of\; mass} + m_{Sphere} (L + R)^{2} = \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} (L + R)^{2}; \\ I_{total} & = I_{Rod} + I_{Sphere} = \frac{1}{3} m_{Rod} L^{2} + \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} (L + R)^{2}; \\ I_{total} & = \frac{1}{3} (20\; kg)(0.5\; m)^{2} + \frac{2}{5} (1.0\; kg)(0.2\; m)^{2} + (1.0\; kg)(0.5\; m + 0.2\; m)^{2}; \\ I_{total} & = (0.167 + 0.016 + 0.490)\; kg\; \cdotp m^{2} = 0.673\; kg\; \cdotp m^{2} \ldotp \end{split}\]

b.

\[\begin{split} I_{Sphere} & = \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} R^{2}; \\ I_{total} & = I_{Rod} + I_{Sphere} = \frac{1}{3} m_{Rod} L^{2} + \frac{2}{5} (1.0\; kg)(0.2\; m)^{2} + (1.0\; kg)(0.2\; m)^{2}; \\ I_{total} & = (0.167 + 0.016 + 0.04)\; kg\; \cdotp m^{2} = 0.223\; kg\; \cdotp m^{2} \ldotp \end{split}\]

Significância

O uso do teorema do eixo paralelo facilita o cálculo do momento de inércia dos objetos compostos. Vemos que o momento de inércia é maior em (a) do que (b). Isso ocorre porque o eixo de rotação está mais próximo do centro de massa do sistema em (b). A analogia simples é a de uma vara. O momento de inércia em torno de uma extremidade é\(\frac{1}{3}\) mL ², mas o momento de inércia através do centro de massa ao longo de seu comprimento é\(\frac{1}{12}\) mL ².

Exemplo\(\PageIndex{3}\): Angular Velocity of a Pendulum

Um pêndulo em forma de haste (Figura\(\PageIndex{8}\)) é liberado do repouso em um ângulo de 30°. Tem 30 cm de comprimento e massa de 300 g. Qual é a velocidade angular no ponto mais baixo?

Figura\(\PageIndex{8}\): Um pêndulo na forma de uma haste é liberado do repouso em um ângulo de 30°.

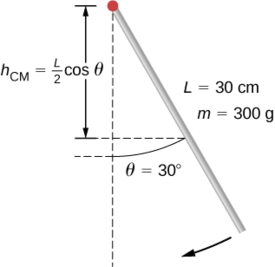
Estratégia

Use a conservação de energia para resolver o problema. No ponto de liberação, o pêndulo tem energia potencial gravitacional, que é determinada a partir da altura do centro de massa acima de seu ponto mais baixo no balanço. Na parte inferior do balanço, toda a energia potencial gravitacional é convertida em energia cinética rotacional.

Solução

A mudança na energia potencial é igual à mudança na energia cinética rotacional,\(\Delta U + \Delta K = 0\).

No topo do swing:

\[U = mgh_{cm} = mgL^2 (\cos \theta). \nonumber \]

Na parte inferior do balanço,

\[U = mg \frac{L}{2}. \nonumber\]

No topo do balanço, a energia cinética rotacional é K = 0. Na parte inferior do balanço, K =\(\frac{1}{2} I \omega^{2}\). Portanto:

\[\Delta U + \Delta K = 0 \Rightarrow (mg \frac{L}{2} (1 - \cos \theta) - 0) + (0 - \frac{1}{2} I \omega^{2}) = 0 \nonumber\]

ou

\[\frac{1}{2} I \omega^{2} = mg \frac{L}{2} (1 - \cos \theta) \ldotp \nonumber\]

Resolvendo para\(\omega\), temos

\[\omega = \sqrt{mg \frac{L}{I} (1 - \cos \theta)} = \sqrt{mg \frac{L}{\frac{1}{3} mL^{2}} (1 - \cos \theta)} = \sqrt{g \frac{3}{L} (1 - \cos \theta)} \ldotp \nonumber\]

Inserindo valores numéricos, temos

\[\omega = \sqrt{(9.8\; m/s^{2}) \left(\dfrac{3}{0.3\; m}\right) (1 - \cos 30)} = 3.6\; rad/s \ldotp \nonumber\]

Significância

Observe que a velocidade angular do pêndulo não depende de sua massa.