10.5: Momento de inércia e energia cinética rotacional
- Page ID
- 185123
- Descreva as diferenças entre a energia cinética rotacional e translacional
- Defina o conceito físico de momento de inércia em termos da distribuição de massa do eixo rotacional
- Explique como o momento de inércia de corpos rígidos afeta sua energia cinética rotacional
- Use a conservação de energia mecânica para analisar sistemas em rotação e translação
- Calcule a velocidade angular de um sistema rotativo quando há perdas de energia devido a forças não conservadoras
Até agora, neste capítulo, trabalhamos com a cinemática rotacional: a descrição do movimento de um corpo rígido rotativo com um eixo de rotação fixo. Nesta seção, definimos duas novas quantidades que são úteis para analisar as propriedades de objetos em rotação: momento de inércia e energia cinética rotacional. Com essas propriedades definidas, teremos duas ferramentas importantes de que precisamos para analisar a dinâmica rotacional.
Energia cinética rotacional
Qualquer objeto em movimento tem energia cinética. Sabemos como calcular isso para um corpo em movimento translacional, mas que tal para um corpo rígido em rotação? Isso pode parecer complicado porque cada ponto do corpo rígido tem uma velocidade diferente. No entanto, podemos usar a velocidade angular — que é a mesma para todo o corpo rígido — para expressar a energia cinética de um objeto em rotação. \(\PageIndex{1}\)A figura mostra um exemplo de um corpo rotativo muito energético: um rebolo elétrico impulsionado por um motor. Faíscas estão voando e ruídos e vibrações são gerados à medida que a pedra de amolar faz seu trabalho. Esse sistema tem energia considerável, parte dela na forma de calor, luz, som e vibração. No entanto, a maior parte dessa energia está na forma de energia cinética rotacional.
A energia no movimento rotacional não é uma nova forma de energia; ao contrário, é a energia associada ao movimento rotacional, a mesma energia cinética no movimento translacional. No entanto, como a energia cinética é dada por\(K=\frac{1}{2}mv^2\), e a velocidade é uma quantidade que é diferente para cada ponto em um corpo rotativo em torno de um eixo, faz sentido encontrar uma maneira de escrever energia cinética em termos da variável\(\omega\), que é a mesma para todos os pontos em um corpo rotativo rígido. Para uma única partícula girando em torno de um eixo fixo, isso é fácil de calcular. Podemos relacionar a velocidade angular com a magnitude da velocidade translacional usando a relação\(v_t=\omega r\), onde\(r\) é a distância da partícula do eixo de rotação e\(v_t\) é sua velocidade tangencial. Substituindo na equação a energia cinética, encontramos
\[ K=\frac{1}{2} m v_{t}^{2}=\frac{1}{2} m(\omega r)^{2}=\frac{1}{2}\left(m r^{2}\right) \omega^{2}. \nonumber \]
No caso de um corpo rígido rotativo, podemos dividir qualquer corpo em um grande número de massas menores, cada uma com uma massa\(m_j\) e distância até o eixo de rotação\(r_j\), de forma que a massa total do corpo seja igual à soma das massas individuais:\(M=\sum_{j} m_{j}\). Cada massa menor tem velocidade tangencial\(v_j\), onde descartamos o\(t\) subscrito no momento. A energia cinética total do corpo rotativo rígido é
\[ K=\sum_{j} \frac{1}{2} m_{j} v_{j}^{2}=\sum_{j} \frac{1}{2} m_{j}\left(r_{j} \omega_{j}\right)^{2} \nonumber \]
e, uma vez que\(\omega_j = \omega\) para todas as massas,
\[ K=\frac{1}{2}\left(\sum_{j} m_{j} r_{j}^{2}\right) \omega^{2} . \label{10.16} \]
As unidades da Equação\ ref {10.16} são joules (J). A equação neste formulário é completa, mas estranha; precisamos encontrar uma maneira de generalizá-la.
Momento de inércia
Se compararmos a Equação\ ref {10.16} com a forma como escrevemos a energia cinética no trabalho e a energia cinética, (\(\frac{1}{2}mv^2\)), isso sugere que temos uma nova variável rotacional para adicionar à nossa lista de relações entre variáveis rotacionais e translacionais. A quantidade\(\sum_{j} m_{j} r_{j}^{2}\) é a contrapartida da massa na equação da energia cinética rotacional. Este é um novo termo importante para movimento rotacional. Essa quantidade é chamada de momento de inércia\(I\), com unidades de kg · m 2:
\[ I=\sum_{j} m_{j} r_{j}^{2} . \label{10.17} \]
Por enquanto, deixamos a expressão na forma de soma, representando o momento de inércia de um sistema de partículas pontuais girando em torno de um eixo fixo. Observamos que o momento de inércia de uma partícula de ponto único em torno de um eixo fixo é simples\(mr^2\),\(r\) sendo a distância da partícula pontual ao eixo de rotação. Na próxima seção, exploraremos a forma integral dessa equação, que pode ser usada para calcular o momento de inércia de alguns corpos rígidos de formato regular.
O momento de inércia é a medida quantitativa da inércia rotacional, assim como no movimento translacional, e a massa é a medida quantitativa da inércia linear, ou seja, quanto mais massivo é um objeto, mais inércia ele tem e maior é sua resistência à mudança na velocidade linear. Da mesma forma, quanto maior o momento de inércia de um corpo rígido ou sistema de partículas, maior é sua resistência à mudança na velocidade angular em torno de um eixo fixo de rotação. É interessante ver como o momento de inércia varia com r, a distância até o eixo de rotação das partículas de massa na Equação\ ref {10.17}. Corpos rígidos e sistemas de partículas com mais massa concentrada a uma distância maior do eixo de rotação têm maiores momentos de inércia do que corpos e sistemas da mesma massa, mas concentrados perto do eixo de rotação. Dessa forma, podemos ver que um cilindro oco tem mais inércia rotacional do que um cilindro sólido da mesma massa ao girar em torno de um eixo através do centro. Substituindo a Equação\ ref {10.17} pela Equação\ ref {10.16}, a expressão para a energia cinética de um corpo rígido rotativo torna-se
\[ K=\frac{1}{2} I \omega^{2} . \label{10.18} \]
Vemos nessa equação que a energia cinética de um corpo rígido rotativo é diretamente proporcional ao momento de inércia e ao quadrado da velocidade angular. Isso é explorado em dispositivos de armazenamento de energia de volante, que são projetados para armazenar grandes quantidades de energia cinética rotacional. Muitas montadoras agora estão testando dispositivos de armazenamento de energia do volante em seus automóveis, como o volante, ou sistema de recuperação de energia cinética, mostrado na Figura\(\PageIndex{2}\).

As quantidades rotacionais e translacionais para energia cinética e inércia estão resumidas na Tabela 10.4. A coluna de relacionamento não está incluída porque não existe uma constante pela qual poderíamos multiplicar a quantidade rotacional para obter a quantidade translacional, como pode ser feito para as variáveis na Tabela 10.3.
| Rotacional | Translacional |
|---|---|
| \(I=\sum_{j} m_{j} r_{j}^{2}\) | \(m\) |
| \(K = \frac{1}{2}I \omega^2\) | \(K = \frac{1}{2} m v^2 \) |
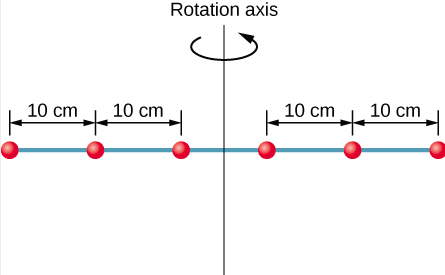
Seis arruelas pequenas estão espaçadas 10 cm de distância em uma haste de massa insignificante e 0,5 m de comprimento. A massa de cada arruela é de 20 g. A haste gira em torno de um eixo localizado a 25 cm, conforme mostrado na Figura\(\PageIndex{3}\). (a) Qual é o momento de inércia do sistema? (b) Se as duas arruelas mais próximas do eixo forem removidas, qual é o momento de inércia das quatro arruelas restantes? (c) Se o sistema com seis arruelas girar a 5 rotações/s, qual é sua energia cinética rotacional?
Estratégia
- Usamos a definição de momento de inércia para um sistema de partículas e realizamos a soma para avaliar essa quantidade. As massas são todas iguais, então podemos colocar essa quantidade na frente do símbolo de soma.
- Nós fazemos um cálculo semelhante.
- Nós inserimos o resultado de (a) na expressão da energia cinética rotacional.
Solução
- \(I=\sum m_{j} r_{j}^{2}=(0.02 \: \mathrm{kg})\left(2 \times(0.25 \: \mathrm{m})^{2}+2 \times(0.15 \: \mathrm{m})^{2}+2 \times(0.05 \: \mathrm{m})^{2}\right)=0.0035 \: \mathrm{kg} \cdot \mathrm{m}^{2}\)
- \(I=\sum_{j} m_{j} r_{j}^{2}=(0.02 \: \mathrm{kg})\left(2 \times(0.25 \: \mathrm{m})^{2}+2 \times(0.15 \: \mathrm{m})^{2}\right)=0.0034 \: \mathrm{kg} \cdot \mathrm{m}^{2}\)
- \(K=\frac{1}{2} I \omega^{2}=\frac{1}{2}\left(0.0035 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(5.0 \times 2 \pi \: \mathrm{rad} / \mathrm{s})^{2}=1.73 \: \mathrm{J}\)
Significância
Podemos ver as contribuições individuais para o momento de inércia. As massas próximas ao eixo de rotação têm uma contribuição muito pequena. Quando os removemos, isso teve um efeito muito pequeno no momento de inércia.
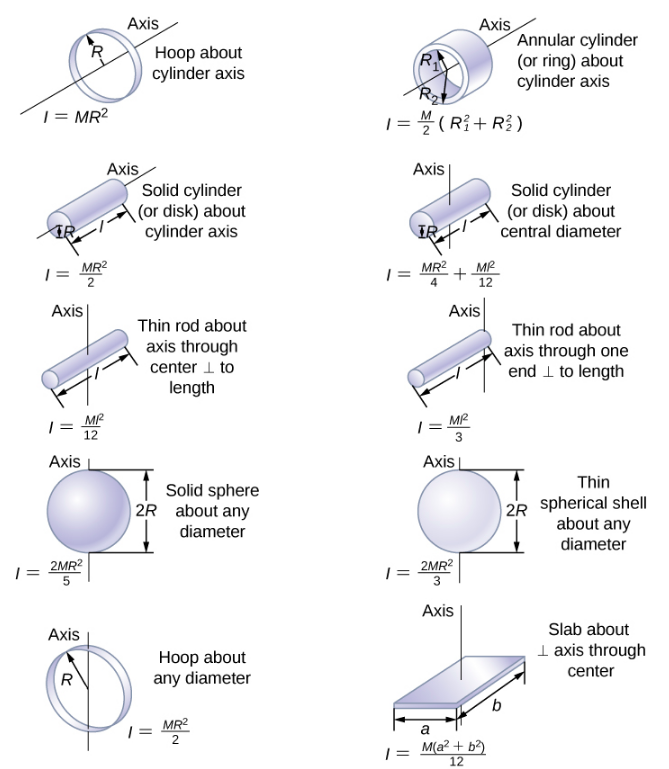
Na próxima seção, generalizamos a equação de soma para partículas pontuais e desenvolvemos um método para calcular momentos de inércia para corpos rígidos. Por enquanto, porém, a Figura\(\PageIndex{4}\) fornece valores de inércia rotacional para formas comuns de objetos em torno de eixos especificados.
Aplicação de energia cinética rotacional
Agora vamos aplicar as ideias de energia cinética rotacional e a tabela de momentos de inércia para ter uma ideia da energia associada a alguns objetos em rotação. Os exemplos a seguir também ajudarão você a se familiarizar com o uso dessas equações. Primeiro, vamos analisar uma estratégia geral de resolução de problemas para energia rotacional.
- Determine se a energia ou o trabalho estão envolvidos na rotação.
- Determine o sistema de interesse. Um esboço geralmente ajuda.
- Analise a situação para determinar os tipos de trabalho e energia envolvidos.
- Se não houver perdas de energia devido ao atrito e outras forças não conservadoras, a energia mecânica é conservada, ou seja,\(K_i + U_i = K_f + U_f\).
- Se forças não conservadoras estiverem presentes, a energia mecânica não é conservada e outras formas de energia, como calor e luz, podem entrar ou sair do sistema. Determine o que são e calcule-os conforme necessário.
- Elimine termos sempre que possível para simplificar a álgebra.
- Avalie a solução numérica para ver se ela faz sentido na situação física apresentada na redação do problema.
Um pequeno helicóptero de resgate típico tem quatro pás: cada uma tem 4,00 m de comprimento e uma massa de 50,0 kg (Figura\(\PageIndex{5}\)). As lâminas podem ser aproximadas como hastes finas que giram em torno de uma extremidade de um eixo perpendicular ao seu comprimento. O helicóptero tem uma massa total carregada de 1000 kg. (a) Calcule a energia cinética rotacional nas pás quando elas giram a 300 rpm. (b) Calcule a energia cinética translacional do helicóptero quando ele voa a 20,0 m/s e compare-a com a energia rotacional nas pás.

Estratégia
As energias cinéticas rotacionais e translacionais podem ser calculadas a partir de suas definições. A redação do problema fornece todas as constantes necessárias para avaliar as expressões das energias cinéticas rotacional e translacional.
Solução
a. A energia cinética rotacional é
\[ K = \frac{1}{2} I \omega^2 \nonumber \]
Devemos converter a velocidade angular em radianos por segundo e calcular o momento de inércia antes de podermos encontrar\(K\). A velocidade angular\(\omega\) é
\[ \omega=\frac{300 \text { rev }}{1.00 \min } \frac{2 \pi \text { rad }}{1 \text { rev }} \frac{1.00 \: \min }{60.0 \: \mathrm{s}}=31.4 \: \frac{\mathrm{rad}}{\mathrm{s}}. \nonumber \]
O momento de inércia de uma lâmina é o de uma haste fina girada em torno de sua extremidade, listado na Figura\(\PageIndex{4}\). O total\(I\) é quatro vezes esse momento de inércia porque há quatro lâminas. Assim,
\[ I=4 \frac{M l^{2}}{3}=4 \times \frac{(50.0 \: \mathrm{kg})(4.00 \: \mathrm{m})^{2}}{3}=1067.0 \: \mathrm{kg} \cdot \mathrm{m}^{2} \nonumber .\]
Ao entrar\(\omega\) e\(I\) entrar na expressão da energia cinética rotacional, obtém-se
\[ K=0.5\left(1067 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(31.4 \: \mathrm{rad} / \mathrm{s})^{2}=5.26 \times 10^{5} \: \mathrm{J}. \nonumber \]
b. Inserindo os valores dados na equação da energia cinética translacional, obtemos
\[ K=\frac{1}{2} m v^{2}=(0.5)(1000.0 \: \mathrm{kg})(20.0 \: \mathrm{m} / \mathrm{s})^{2}=2.00 \times 10^{5} \: \mathrm{J} . \nonumber \]
Para comparar as energias cinéticas, tomamos a razão entre a energia cinética translacional e a energia cinética rotacional. Essa proporção é
\[ \frac{2.00 \times 10^{5} \: \mathrm{J}}{5.26 \times 10^{5} \: \mathrm{J}}=0.380 . \nonumber \]
Significância
A razão entre a energia translacional e a energia cinética rotacional é de apenas 0,380. Essa proporção nos diz que a maior parte da energia cinética do helicóptero está em suas pás giratórias.
Uma pessoa lança um bumerangue no ar com uma velocidade de 30,0 m/s em um ângulo de 40,0° em relação à horizontal (Figura\(\PageIndex{6}\)). Ele tem uma massa de 1,0 kg e gira a 10,0 rotações/s. O momento de inércia do bumerangue é dado como\(I=\frac{1}{12} m L^{2} \) onde\(L\) = 0,7 m. (a) Qual é a energia total do bumerangue quando ele sai da mão? (b) Qual a altura que o bumerangue vai da elevação da mão, negligenciando a resistência do ar?
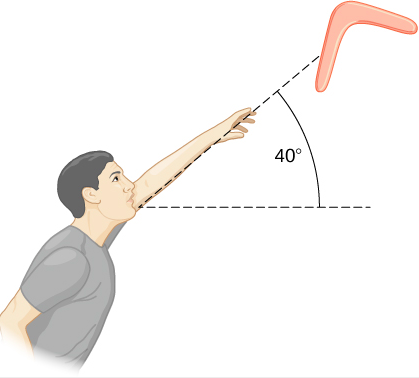
Estratégia
Usamos as definições de energia cinética rotacional e linear para encontrar a energia total do sistema. O problema é negligenciar a resistência do ar, então não precisamos nos preocupar com a perda de energia. Na parte (b), usamos a conservação da energia mecânica para encontrar a altura máxima do bumerangue.
Solução
a. Momento de inércia:\( I=\frac{1}{12} m L^{2}=\frac{1}{12}(1.0 \: \mathrm{kg})(0.7 \: \mathrm{m})^{2}=0.041 \: \mathrm{kg} \cdot \mathrm{m}^{2}. \)
Velocidade angular:\( \omega=(10.0 \: \mathrm{rev} / \mathrm{s})(2 \pi)=62.83 \: \mathrm{rad} / \mathrm{s} \)
A energia cinética rotacional é, portanto,
\[ K_{R}=\frac{1}{2}\left(0.041 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(62.83 \: \mathrm{rad} / \mathrm{s})^{2}=80.93 \: \mathrm{J} \nonumber \]
A energia cinética translacional é
\[ K_{\mathrm{T}}=\frac{1}{2} m v^{2}=\frac{1}{2}(1.0 \: \mathrm{kg})(30.0 \: \mathrm{m} / \mathrm{s})^{2}=450.0 \: \mathrm{J} \nonumber \]
Assim, a energia total no bumerangue é
\[ K_{\text {Total }}=K_{R}+K_{T}=80.93+450.0=530.93 \: \mathrm{J}. \nonumber \]
b. Usamos a conservação de energia mecânica. Como o bumerangue é lançado em um ângulo, precisamos escrever as energias totais do sistema em termos de suas energias cinéticas lineares usando a velocidade nas direções x e y. A energia total quando o bumerangue sai da mão é
\[ E_{\text {Before }}=\frac{1}{2} m v_{x}^{2}+\frac{1}{2} m v_{y}^{2}+\frac{1}{2} I \omega^{2} \nonumber \]
A energia total na altura máxima é
\[ E_{\text {Final }}=\frac{1}{2} m v_{x}^{2}+\frac{1}{2} I \omega^{2}+m g h \nonumber \]
Pela conservação da energia mecânica,\(E_{Before} = E_{Final}\) então temos, depois de cancelar termos semelhantes,
\[ \frac{1}{2} m v_{y}^{2}=m g h \nonumber .\]
Desde\(v_y\) = 30,0 m/s (\(\sin 40^{\circ}\)) = 19,28 m/s, encontramos
\[ h=\frac{(19.28 \: \mathrm{m} / \mathrm{s})^{2}}{2\left(9.8 \: \mathrm{m} / \mathrm{s}^{2}\right)}=18.97 \: \mathrm{m} \nonumber \]
Significância
Na parte (b), a solução demonstra como a conservação de energia é um método alternativo para resolver um problema que normalmente seria resolvido usando cinemática. Na ausência de resistência do ar, a energia cinética rotacional não foi um fator na solução para a altura máxima.
Uma hélice submarina nuclear tem um momento de inércia de 800,0 kg • m 2. Se a hélice submersa tiver uma taxa de rotação de 4,0 rotações/s quando o motor é cortado, qual é a taxa de rotação da hélice após 5,0 s quando a resistência à água retirou 50.000 J do sistema?


