7.4: Teorema da Energia do Trabalho
- Page ID
- 185285
- Aplique o teorema da energia de trabalho para encontrar informações sobre o movimento de uma partícula, dadas as forças que atuam sobre ela
- Use o teorema da energia de trabalho para encontrar informações sobre as forças que atuam sobre uma partícula, dadas informações sobre seu movimento
Discutimos como encontrar o trabalho realizado em uma partícula pelas forças que atuam sobre ela, mas como esse trabalho se manifesta no movimento da partícula? De acordo com a segunda lei do movimento de Newton, a soma de todas as forças que atuam sobre uma partícula, ou a força líquida, determina a taxa de mudança no momento da partícula, ou seu movimento. Portanto, devemos considerar o trabalho realizado por todas as forças que atuam sobre uma partícula, ou a rede, para ver o efeito que ela tem no movimento da partícula.
Vamos começar examinando a rede realizada em uma partícula à medida que ela se move sobre um deslocamento infinitesimal, que é o produto escalar da força líquida e do deslocamento:
\[dW_{net} = \vec{F}_{net} \cdotp d \vec{r}. \nonumber\]
A segunda lei de Newton nos diz que
\[\vec{F}_{net} = m \left(\dfrac{d \vec{v}}{dt}\right) \nonumber\]
então
\[dW_{net} = m \left(\dfrac{d \vec{v}}{dt}\right) \cdotp d \vec{r}. \nonumber\]
Para as funções matemáticas que descrevem o movimento de uma partícula física, podemos reorganizar os diferenciais dt, etc., como quantidades algébricas nessa expressão, ou seja,
\[\begin{align*} dW_{net} &= m \left(\dfrac{d \vec{v}}{dt}\right) \cdotp d \vec{r} \\[4pt] &= m\, d \vec{v}\; \cdotp \left(\dfrac{d \vec{r}}{dt}\right) \\[4pt] &= m \vec{v}\; \cdotp d \vec{v}, \end{align*}\]
onde substituímos a velocidade pela derivada temporal do deslocamento e usamos a propriedade comutativa do produto escalar. Como derivadas e integrais de escalares provavelmente são mais familiares para você neste momento, expressamos o produto escalar em termos de coordenadas cartesianas antes de integrarmos dois pontos A e B na trajetória da partícula. Isso nos dá o trabalho de rede realizado na partícula:
\[\begin{align} W_{net,\; AB} & = \int_{A}^{B} (mv_{x} dv_{x} + mv_{y}dv_{y} + mv_{z}dv_{z} \\[4pt] & = \frac{1}{2} m \left| v_{x}^{2} + v_{y}^{2} + v_{z}^{2} \right|_{A}^{B} = \left|\frac{1}{2} mv^{2} \right|_{A}^{B} = K_{B} - K_{A} \ldotp \end{align} \label{7.8}\]
Na etapa intermediária, usamos o fato de que o quadrado da velocidade é a soma dos quadrados de seus componentes cartesianos e, na última etapa, usamos a definição da energia cinética da partícula. Esse resultado importante é chamado de teorema trabalho-energia.
O trabalho em rede realizado em uma partícula é igual à mudança na energia cinética da partícula:
\[W_{net} = K_{B} - K_{A} \ldotp \label{7.9}\]

De acordo com esse teorema, quando um objeto fica mais lento, sua energia cinética final é menor que sua energia cinética inicial, a mudança em sua energia cinética é negativa, assim como o trabalho em rede feito nele. Se um objeto acelerar, o trabalho de rede realizado nele é positivo. Ao calcular a rede, você deve incluir todas as forças que atuam sobre um objeto. Se você omitir qualquer força que atue sobre um objeto, ou se incluir qualquer força que não atue sobre ele, você obterá um resultado errado.
A importância do teorema trabalho-energia, e das generalizações adicionais às quais ele leva, é que ele torna alguns tipos de cálculos muito mais simples de realizar do que seriam tentando resolver a segunda lei de Newton. Por exemplo, na seção sobre as Leis do Movimento de Newton, descobrimos a velocidade de um objeto deslizando por um plano sem atrito resolvendo a segunda lei de Newton para a aceleração e usando equações cinemáticas para aceleração constante, obtendo
\[v_{f}^{2} = v_{i}^{2} + 2g(s_{f} - s_{i}) \sin \theta,\]
onde\(s\) está o deslocamento no avião.
Também podemos obter esse resultado do teorema da energia do trabalho (Equação\ ref {7.9}). Como apenas duas forças estão atuando sobre o objeto — a gravidade e a força normal — e a força normal não faz nenhum trabalho, a rede é apenas o trabalho feito pela gravidade. Isso depende apenas do peso do objeto e da diferença de altura, então
\[W_{net} = W_{grav} = -mg (y_{f} - y_{i}),\]
onde\(y\) está positivo. O teorema da energia do trabalho diz que isso é igual à mudança na energia cinética:
\[-mg (y_{f} - y_{i}) = \frac{1}{2} (v_{f}^{2} - v_{i}^{2}) \ldotp\]
Usando um triângulo reto, podemos ver que
\[(y_f − y_i) = (s_f − s-i)\sin \theta, \nonumber\]
então o resultado da velocidade final é o mesmo.
O que se ganha com o uso do teorema trabalho-energia? A resposta é que, para uma superfície plana sem atrito, não muito. No entanto, a segunda lei de Newton é fácil de resolver apenas para esse caso específico, enquanto o teorema da energia de trabalho fornece a velocidade final para qualquer superfície sem atrito moldada. Para uma superfície curva arbitrária, a força normal não é constante, e a segunda lei de Newton pode ser difícil ou impossível de resolver analiticamente. Constante ou não, para o movimento ao longo de uma superfície, a força normal nunca funciona, porque é perpendicular ao deslocamento. Um cálculo usando o teorema trabalho-energia evita essa dificuldade e se aplica a situações mais gerais.
- Desenhe um diagrama de corpo livre para cada força no objeto.
- Determine se cada força funciona ou não sobre o deslocamento no diagrama. Certifique-se de manter quaisquer sinais positivos ou negativos no trabalho realizado.
- Some a quantidade total de trabalho realizado por cada força.
- Defina esse trabalho total igual à mudança na energia cinética e resolva qualquer parâmetro desconhecido.
- Verifique suas respostas. Se o objeto estiver viajando a uma velocidade constante ou aceleração zero, o trabalho total realizado deve ser zero e corresponder à mudança na energia cinética. Se o trabalho total for positivo, o objeto deve ter acelerado ou aumentado a energia cinética. Se o trabalho total for negativo, o objeto deve ter diminuído ou diminuído a energia cinética
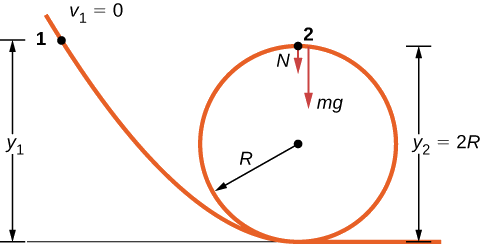
A pista sem atrito de um carro de brinquedo inclui um circuito de raio\(R\). Qual a altura, medida a partir da parte inferior do circuito, o carro deve ser colocado para partir do repouso na seção de aproximação da pista e percorrer toda a volta?
Estratégia
O diagrama de corpo livre na posição final do objeto é desenhado na Figura\(\PageIndex{2}\). O trabalho gravitacional é o único trabalho realizado sobre o deslocamento que não é zero. Como o peso aponta na mesma direção do deslocamento vertical líquido, o trabalho total realizado pela força gravitacional é positivo. A partir do teorema da energia de trabalho, a altura inicial determina a velocidade do carro no topo do circuito,
\[mg(y_{2} - y_{1}) = \dfrac{1}{2} mv_{2}^{2}, \nonumber\]
onde a notação é mostrada na figura anexa. No topo do circuito, a força e a gravidade normais estão baixas e a aceleração é centrípeta, então
\[a_{top} = \dfrac{F}{m} = \dfrac{N + mg}{m} = \frac{v_{2}^{2}}{R} \ldotp \nonumber\]
A condição para manter contato com a pista é que deve haver alguma força normal, por menor que seja; ou seja,\(N > 0\). Substituindo por\(v_{2}^{2}\) e\(N\), podemos encontrar a condição para\(y_1\).
Solução
Implemente as etapas da estratégia para chegar ao resultado desejado:
\[N = -mg + \frac{mv_{2}^{2}}{R} = \frac{-mgR + 2mg(y_{1} - 2R)}{R} > 0\; or\; y_{1} > \frac{5R}{2} \ldotp \nonumber\]
Significância
Na superfície do circuito, o componente normal da gravidade e a força de contato normal devem fornecer a aceleração centrípeta do carro que contorna o circuito. O componente tangencial da gravidade diminui ou acelera o carro. Uma criança descobriria a que altura dar partida no carro por tentativa e erro, mas agora que você conhece o teorema da energia de trabalho, pode prever a altura mínima (bem como outros resultados mais úteis) a partir de princípios físicos. Usando o teorema da energia de trabalho, você não precisou resolver uma equação diferencial para determinar a altura.
Suponha que o raio do loop no Exemplo\(\PageIndex{1}\) seja de 15 cm e o carrinho de brinquedo comece do repouso a uma altura de 45 cm acima da parte inferior. Qual é a velocidade na parte superior do circuito?
Em situações em que o movimento de um objeto é conhecido, mas os valores de uma ou mais das forças que atuam sobre ele não são conhecidos, você pode usar o teorema da energia de trabalho para obter algumas informações sobre as forças. O trabalho depende da força e da distância sobre a qual ele atua, portanto, as informações são fornecidas por meio de seu produto.
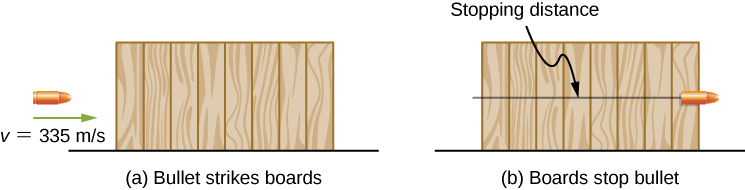
Uma bala tem uma massa de 40 grãos (2,60 g) e uma velocidade de focinho de 1100 pés. /s (335 m/s). Ele pode penetrar oito tábuas de pinho de 1 polegada, cada uma com espessura de 0,75 polegadas. Qual é a força média de parada exercida pela madeira, conforme mostrado na Figura\(\PageIndex{3}\)?
Estratégia
Podemos supor que, nas condições gerais estabelecidas, a bala perde toda a sua energia cinética penetrando nas placas, então o teorema da energia de trabalho diz que sua energia cinética inicial é igual à força média de parada vezes a distância penetrada. A mudança na energia cinética da bala e o trabalho em rede feito para pará-la são negativas, então quando você escreve o teorema da energia de trabalho, com a rede igual à força média vezes a distância de parada, é isso que você obtém. A espessura total de oito tábuas de pinho de 1 polegada que a bala penetra é de 8 x\(\frac{3}{4}\) pol. = 6 pol. = 15,2 cm.
Solução
Aplicando o teorema trabalho-energia, obtemos
\[W_{net} = - F_{ave} \Delta s_{stop} = - K_{initial} , \nonumber\]
então
\[F_{ave} = \frac{\frac{1}{2} mv^{2}}{\Delta s_{stop}} = \frac{\frac{1}{2} (2.66 \times 10^{-3}\; kg)(335\; m/s)^{2}}{0.152\; m} = 960\; N \ldotp \nonumber\]
Significância
Poderíamos ter usado a segunda lei e a cinemática de Newton neste exemplo, mas o teorema trabalho-energia também fornece uma resposta para situações menos simples. A penetração de uma bala, disparada verticalmente para cima em um bloco de madeira, é discutida em uma seção do artigo recente de Asif Shakur [“Bullet-Block Science Video Puzzle”. O professor de física (janeiro de 2015) 53 (1): 15-16]. Se a bala for disparada no ponto morto do bloco, ela perde toda a sua energia cinética e penetra um pouco mais longe do que se fosse disparada fora do centro. O motivo é que, se a bala cair fora do centro, ela tem um pouco de energia cinética depois de parar de penetrar, porque o bloco gira. O teorema da energia de trabalho implica que uma mudança menor na energia cinética resulta em uma menor penetração. Você entenderá mais sobre física neste interessante artigo depois de terminar de ler Angular Momentum.
Saiba mais sobre trabalho e energia nesta simulação PhET (https://phet.colorado.edu/en/simulation/the-ramp) chamada “a rampa”. Tente mudar a força que empurra a caixa e a força de atrito ao longo da inclinação. Os gráficos de trabalho e energia podem ser examinados para observar o trabalho total realizado e a mudança na energia cinética da caixa.


