Skip to main content
Global

4.6: Movimento relativo em uma e duas dimensões

  1. Last updated
  2. Save as PDF
  • Page ID
    185336

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de
    • Explique o conceito de quadros de referência.
    • Escreva as equações vetoriais de posição e velocidade para o movimento relativo.
    • Desenhe os vetores de posição e velocidade para o movimento relativo.
    • Analise problemas de movimento relativo unidimensional e bidimensional usando as equações vetoriais de posição e velocidade.

    O movimento não acontece isoladamente. Se você estiver viajando em um trem movendo-se a 10 m/s para o leste, essa velocidade é medida em relação ao solo no qual você está viajando. No entanto, se outro trem passar por você a 15 m/s leste, sua velocidade em relação a esse outro trem será diferente da sua velocidade em relação ao solo. Sua velocidade em relação ao outro trem é de 5 m/s oeste. Para explorar mais essa ideia, primeiro precisamos estabelecer alguma terminologia.

    Frames de referência

    Para discutir o movimento relativo em uma ou mais dimensões, primeiro introduzimos o conceito de quadros de referência. Quando dizemos que um objeto tem uma certa velocidade, devemos afirmar que ele tem uma velocidade em relação a um determinado quadro de referência. Na maioria dos exemplos que examinamos até agora, esse quadro de referência tem sido a Terra. Se você diz que uma pessoa está sentada em um trem se movendo a 10 m/s para o leste, então você insinua que a pessoa no trem está se movendo em relação à superfície da Terra nessa velocidade, e a Terra é o quadro de referência. Podemos expandir nossa visão do movimento da pessoa no trem e dizer que a Terra está girando em sua órbita ao redor do Sol. Nesse caso, o movimento se torna mais complicado. Nesse caso, o sistema solar é o quadro de referência. Em resumo, toda discussão sobre movimento relativo deve definir os quadros de referência envolvidos. Agora, desenvolvemos um método para nos referirmos a quadros de referência em movimento relativo.

    Movimento relativo em uma dimensão

    Primeiro, introduzimos o movimento relativo em uma dimensão, porque os vetores de velocidade se simplificam para ter apenas duas direções possíveis. Veja o exemplo da pessoa sentada em um trem se movendo para o leste. Se escolhermos o leste como a direção positiva e a Terra como o quadro de referência, podemos escrever a velocidade do trem em relação à Terra como\(\vec{v}_{TE}\) = 10 m/s\(\hat{i}\) leste, onde os subscritos TE se referem ao trem e à Terra. Agora, digamos que a pessoa se levante do assento e caminhe em direção à parte de trás do trem a 2 m/s. Isso nos indica que ela tem uma velocidade em relação à estrutura de referência do trem. Como a pessoa está caminhando para o oeste, na direção negativa, escrevemos sua velocidade em relação ao trem como\(\vec{v}_{PT}\) = −2 m/s\(\hat{i}\). Podemos adicionar os dois vetores de velocidade para encontrar a velocidade da pessoa em relação à Terra. Essa velocidade relativa é escrita como

    \[\vec{v}_{PE} = \vec{v}_{PT} + \vec{v}_{TE} \ldotp \label{4.33}\]

    Observe a ordem dos subscritos para os vários quadros de referência em Equation\ ref {4.33}. Os subscritos do quadro de referência do acoplamento, que é o trem, aparecem consecutivamente no lado direito da equação. A figura\(\PageIndex{1}\) mostra a ordem correta dos subscritos ao formar a equação vetorial.

    alt
    Figura\(\PageIndex{1}\): Ao construir a equação vetorial, os subscritos do quadro de referência do acoplamento aparecem consecutivamente na parte interna. Os subscritos no lado esquerdo da equação são os mesmos dos dois subscritos externos no lado direito da equação.

    Somando os vetores, encontramos\(\vec{v}_{PE}\) = 8 m/s\(\hat{i}\), então a pessoa está se movendo 8 m/s para o leste em relação à Terra. Graficamente, isso é mostrado na Figura\(\PageIndex{2}\).

    Vetores de velocidade do trem em relação à Terra, pessoa em relação ao trem e pessoa em relação à Terra. V sub T E é o vetor de velocidade do trem em relação à Terra. Tem um valor de 10 metros por segundo e é representado como uma longa seta verde apontando para a direita. V sub P T é o vetor de velocidade da pessoa em relação ao trem. Tem valor de -2 metros por segundo e é representado como uma pequena seta verde apontando para a esquerda. V sub P E é o vetor de velocidade da pessoa em relação à Terra. Tem um valor de 8 metros por segundo e é representado como uma seta verde de comprimento médio apontando para a direita.
    Figura\(\PageIndex{2}\): Vetores de velocidade do trem em relação à Terra, pessoa em relação ao trem e pessoa em relação à Terra.

    Velocidade relativa em duas dimensões

    Agora podemos aplicar esses conceitos para descrever o movimento em duas dimensões. Considere uma partícula P e os quadros de referência S e S′s, conforme mostrado na Figura\(\PageIndex{3}\). A posição da origem de S′medida em S é\(\vec{r}_{S'S}\), a posição de P medida em S′s é\(\vec{r}_{PS'}\) e a posição de P medida em S é\(\vec{r}_{PS}\).

    Um sistema de coordenadas x y z é mostrado e rotulado como sistema S. Um segundo sistema de coordenadas, S primo com eixos x primo, y primo, z primo, é deslocado em relação a S. O vetor r sub S primo S, mostrado como uma seta roxa, se estende da origem de S até a origem de S primo. O vetor r sub P S é um vetor da origem de S até um ponto P. O vetor r sub P S prime é um vetor da origem de S primo até o mesmo ponto P. Os vetores r s primo s, r P S prime e r P S formam um triângulo, e r P S é a soma vetorial de r S primo S e r P S primo.
    Figura\(\PageIndex{3}\): As posições da partícula P em relação aos quadros S e S′s são\(\vec{r}_{PS}\) e\(\vec{r}_{PS'}\), respectivamente.

    Da Figura\(\PageIndex{3}\), vemos que

    \[\vec{r}_{PS} = \vec{r}_{PS} + \vec{r}_{S'S} \ldotp \label{4.34}\]

    As velocidades relativas são as derivadas temporais dos vetores de posição. Portanto,

    \[\vec{v}_{PS} = \vec{v}_{PS'} + \vec{v}_{S'S} \ldotp \label{4.35}\]

    A velocidade de uma partícula em relação a S é igual à sua velocidade em relação a S′mais a velocidade de S′em relação a S.

    Podemos estender a Equação\ ref {4,35} para qualquer número de quadros de referência. Para a partícula P com velocidades\(\vec{v}_{PA}\),\(\vec{v}_{PB}\), e\(\vec{v}_{PC}\) nos quadros A, B e C,

    \[\vec{v}_{PC} = \vec{v}_{PA} + \vec{v}_{AB} + \vec{v}_{BC} \ldotp \label{4.36}\]

    Também podemos ver como as acelerações estão relacionadas, conforme observado em dois quadros de referência, diferenciando a Equação\ ref {4.35}:

    \[\vec{a}_{PS} = \vec{a}_{PS'} + \vec{a}_{S'S} \ldotp \label{4.37}\]

    Vemos que se a velocidade de S′em relação a S é uma constante, então\(\vec{a}_{S'S}\) = 0 e

    \[\vec{a}_{PS} = \vec{a}_{PS'} \ldotp \label{4.38}\]

    Isso diz que a aceleração de uma partícula é a mesma medida por dois observadores se movendo a uma velocidade constante em relação um ao outro.

    Exemplo 4.13: Movimento de um carro em relação a um caminhão

    Um caminhão está viajando para o sul a uma velocidade de 70 km/h em direção a um cruzamento. Um carro está viajando para o leste em direção ao cruzamento a uma velocidade de 80 km/h (Figura\(\PageIndex{4}\)). Qual é a velocidade do carro em relação ao caminhão?

    Um caminhão é mostrado viajando para o sul a uma velocidade V abaixo de T E de 70 km/h em direção a um cruzamento. Um carro está viajando para o leste em direção ao cruzamento a uma velocidade V sub C E de 80 km/h
    Figura\(\PageIndex{4}\): Um carro viaja para o leste em direção a um cruzamento, enquanto um caminhão viaja para o sul em direção ao mesmo cruzamento.

    Estratégia

    Primeiro, devemos estabelecer o quadro de referência comum a ambos os veículos, que é a Terra. Em seguida, escrevemos as velocidades de cada um em relação ao quadro de referência da Terra, o que nos permite formar uma equação vetorial que liga o carro, o caminhão e a Terra para resolver a velocidade do carro em relação ao caminhão.

    Solução

    A velocidade do carro em relação à Terra é\(\vec{v}_{CE}\) = 80 km/h\(\hat{i}\). A velocidade do caminhão em relação à Terra é\(\vec{v}_{TE}\) = −70 km/h\(\hat{j}\). Usando a regra de adição de velocidade, a equação de movimento relativo que estamos buscando é

    \[\vec{v}_{CT} = \vec{v}_{CE} + \vec{v}_{ET} \ldotp \label{ex2}\]

    Aqui\(\vec{v}_{CT}\) está a velocidade do carro em relação ao caminhão, e a Terra é o quadro de referência de conexão. Como temos a velocidade do caminhão em relação à Terra, o negativo desse vetor é a velocidade da Terra em relação ao caminhão:\(\vec{v}_{ET} = − \vec{v}_{TE}\). O diagrama vetorial dessa equação é mostrado na Figura\(\PageIndex{5}\).

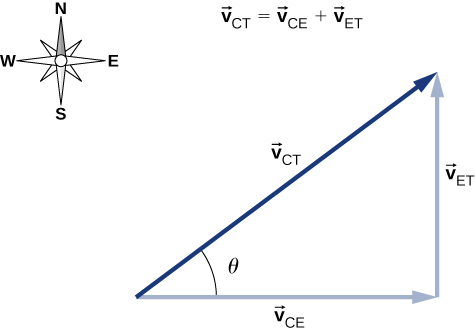
    O triângulo reto formado pelos vetores V sub C E à direita, V sub E T para baixo e V sub C T para cima e para a direita é mostrado V sub C T é a hipotenusa e faz um ângulo de teta com V sub C E. A equação vetorial vetor v sub C T é igual ao vetor C E mais o vetor E T é dado. Uma bússola é mostrada indicando que o norte está para cima, o leste para a direita, o sul para baixo e o oeste para a esquerda.
    Figura\(\PageIndex{5}\): Diagrama vetorial da equação vetorial\ ref {ex2}.

    Agora podemos resolver a velocidade do carro em relação ao caminhão:

    \[\big| \vec{v}_{CT} \big| = \sqrt{(80.0\; km/h)^{2} + (70.0\; km/h)^{2}} = 106.\; km/h \nonumber\]

    e

    \[\theta = \tan^{-1} \left(\dfrac{70.0}{80.0}\right) = 41.2^{o}\; north\; of\; east \ldotp \nonumber\]

    Significância

    Desenhar um diagrama vetorial mostrando os vetores de velocidade pode ajudar a entender a velocidade relativa dos dois objetos.

    Exercício 4.6

    Um barco segue para o norte em águas calmas a 4,5 m/s diretamente através de um rio que corre para o leste a 3,0 m/s. Qual é a velocidade do barco em relação à Terra?

    Exemplo 4.14: Pilotando um avião em um vento

    Um piloto deve pilotar seu avião para o norte para chegar ao seu destino. O avião pode voar a 300 km/h em ar parado. Um vento está soprando do nordeste a 90 km/h. (a) Qual é a velocidade do avião em relação ao solo? (b) Em que direção o piloto deve dirigir seu avião para voar para o norte?

    Estratégia

    O piloto deve apontar seu avião um pouco a leste do norte para compensar a velocidade do vento. Precisamos construir uma equação vetorial que contenha a velocidade do plano em relação ao solo, a velocidade do plano em relação ao ar e a velocidade do ar em relação ao solo. Como essas duas últimas quantidades são conhecidas, podemos resolver a velocidade do avião em relação ao solo. Podemos representar graficamente os vetores e usar esse diagrama para avaliar a magnitude da velocidade do avião em relação ao solo. O diagrama também nos dirá o ângulo que a velocidade do avião faz com o norte em relação ao ar, que é a direção em que o piloto deve dirigir seu avião.

    Solução

    A equação vetorial é\(\vec{v}_{PG} = \vec{v}_{PA} + \vec{v}_{AG}\), onde P = plano, A = ar e G = solo. A partir da geometria na Figura\(\PageIndex{6}\), podemos resolver facilmente a magnitude da velocidade do plano em relação ao solo e o ângulo de direção do avião,\(\theta\).

    Uma bússola mostra que o norte está para cima, o leste para a direita, o sul para baixo e o oeste para a esquerda. Os vetores V sub P G, V sub A G e V sub P A formam um triângulo. Um avião é mostrado no vetor V sub P G, que aponta para cima. V sub P A aponta para cima e para a direita, em um ângulo de teta em relação ao vetor V sub P G. V sub A G aponta para baixo e para a esquerda, em um ângulo de 45 graus abaixo da horizontal. V sub P G é a soma vetorial de v sub P A e V sub A G.
    Figura\(\PageIndex{6}\): Diagrama vetorial da Equação\ ref {4.34} mostrando os vetores\(\vec{v}_{PA}\)\(\vec{v}_{AG}\),\(\vec{v}_{PG}\) e.
    1. Quantidades conhecidas: $$\ big|\ vec {v} _ {PA}\ big| = 300\; km/h$$ $$\ big|\ vec {v} _ {AG}\ big| = 90\; KM/H$$ Substituindo na equação do movimento, obtemos\(\big| \vec{v}_{PG} \big|\) = 230 km/h.
    2. O ângulo\(\theta\) = tan −1\(\left(\dfrac{63.64}{300}\right)\) = 12° a leste do norte.