4.5: Movimento circular uniforme

Last updated
Save as PDF

Page ID: 185340

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Resolva a aceleração centrípeta de um objeto se movendo em um caminho circular.
Use as equações do movimento circular para encontrar a posição, a velocidade e a aceleração de uma partícula executando movimento circular.
Explique as diferenças entre a aceleração centrípeta e a aceleração tangencial resultantes do movimento circular não uniforme.
Avalie a aceleração centrípeta e tangencial em movimentos circulares não uniformes e encontre o vetor de aceleração total.

O movimento circular uniforme é um tipo específico de movimento no qual um objeto viaja em um círculo com uma velocidade constante. Por exemplo, qualquer ponto em uma hélice girando a uma taxa constante está executando um movimento circular uniforme. Outros exemplos são os ponteiros dos segundos, minutos e horas de um relógio. É notável que os pontos desses objetos em rotação estejam realmente acelerando, embora a taxa de rotação seja constante. Para ver isso, devemos analisar o movimento em termos de vetores.

Aceleração centrípeta

Na cinemática unidimensional, objetos com velocidade constante têm aceleração zero. No entanto, na cinemática bidimensional e tridimensional, mesmo que a velocidade seja constante, uma partícula pode ter aceleração se se mover ao longo de uma trajetória curva, como um círculo. Nesse caso, o vetor de velocidade está mudando, ou\(\frac{d\vec{v}}{dt}\) ≠ 0. Isso é mostrado na Figura\(\PageIndex{1}\). À medida que a partícula se move no sentido anti-horário no tempo\(\Delta\) t no caminho circular, seu vetor de posição se move de\(\vec{r}(t)\) para\(\vec{r}(t + \Delta t)\). O vetor de velocidade tem magnitude constante e é tangente ao caminho à medida que muda de\(\vec{v}\) (t) para\(\vec{v}\left(t + \Delta t\right)\), mudando apenas sua direção. Como o vetor de velocidade\(\vec{v}(t)\) é perpendicular ao vetor de posição\(\vec{r}\) (t), os triângulos formados pelos vetores de posição e\(\Delta \vec{r}\), e os vetores de velocidade\(\Delta \vec{v}\) são semelhantes. Além disso, uma vez que

\[|\vec{r}(t) | = | \vec{r} (t + \Delta t)| \nonumber\]

\[| \vec{v} (t)| = | \vec{v} (t + \Delta t)|, \nonumber \]

os dois triângulos são isósceles. A partir desses fatos, podemos fazer a afirmação

\[\dfrac{\Delta v}{v} = \dfrac{\Delta r}{r}\]

\[\Delta v = \dfrac{v}{r} \Delta r.\]

A Figura a mostra um círculo com centro no ponto C. São mostrados o raio r de t e o raio r de t, que são um ângulo Delta teta separado, e o comprimento da corda delta r conectando as extremidades dos dois raios. Os vetores r de t, r de t mais delta t e delta r formam um triângulo. Na ponta do vetor r de t, a velocidade é mostrada como v de t e aponta para cima e para a direita, tangente ao círculo. Na ponta do vetor r de t mais delta t, a velocidade é mostrada como v de t mais delta t e aponta para cima e para a esquerda, tangente ao círculo. A Figura b mostra os vetores v de t e v de t mais delta t com suas caudas juntas, e o vetor delta v da ponta de v de t até a ponta de v de t mais delta t. Esses três vetores formam um triângulo. O ângulo entre v de t e v de t mais delta t é teta. — Figura\(\PageIndex{1}\): (a) Uma partícula está se movendo em um círculo a uma velocidade constante, com vetores de posição\(t\) e\(t + \Delta t\) velocidade às vezes e. (b) Vetores de velocidade formando um triângulo. Os dois triângulos na figura são semelhantes. O vetor\(\Delta \vec{v}\) aponta para o centro do círculo no limite\(\Delta t → 0.\)

Podemos encontrar a magnitude da aceleração a partir de

\[a = \lim_{\Delta t \rightarrow 0} \left(\dfrac{\Delta v}{\Delta t}\right) = \frac{v}{r} \left(\lim_{\Delta t \rightarrow 0} \dfrac{\Delta r}{\Delta t}\right) = \frac{v^{2}}{r} \ldotp\]

A direção da aceleração também pode ser encontrada observando que quando\(\Delta\) t e, portanto, se\(\Delta \theta\) aproxima de zero, o vetor\(\Delta \vec{v}\) se aproxima de uma direção perpendicular\(\vec{v}\) a. No limite\(\Delta t → 0,\)\(\Delta \vec{v}\) é perpendicular\(\vec{v}\) a. Como\(\vec{v}\) é tangente à circunferência, a aceleração\(\frac{d \vec{v}}{dt}\) aponta para o centro da circunferência. Resumindo, uma partícula que se move em um círculo a uma velocidade constante tem uma aceleração com magnitude

\[a_{c} = \frac{v^{2}}{r} \ldotp \label{4.27}\]

A direção do vetor de aceleração é em direção ao centro do círculo (Figura\(\PageIndex{2}\)). Essa é uma aceleração radial e é chamada de aceleração centrípeta, e é por isso que damos a ela o subscrito\(c\). A palavra centrípeta vem das palavras latinas centrum (que significa “centro”) e petere (que significa “buscar”) e, portanto, assume o significado de “busca de centro”.

Um círculo é mostrado com uma seta roxa rotulada como vetor a sub c apontando radialmente para dentro e uma seta verde tangente ao círculo e rotulada v. As setas são mostradas com suas pontas no mesmo ponto do círculo. — Figura\(\PageIndex{2}\): O vetor de aceleração centrípeta aponta para o centro do caminho circular do movimento e é uma aceleração na direção radial. O vetor de velocidade também é mostrado e é tangente ao círculo.

Vamos investigar alguns exemplos que ilustram as magnitudes relativas da velocidade, do raio e da aceleração centrípeta.

Exemplo\(\PageIndex{1}\): Creating an Acceleration of 1 g

Um jato está voando a 134,1 m/s ao longo de uma linha reta e faz uma curva ao longo de um caminho circular ao nível do solo. Qual deve ser o raio do círculo para produzir uma aceleração centrípeta de 1 g no piloto e um jato em direção ao centro da trajetória circular?

Estratégia

Dada a velocidade do jato, podemos resolver o raio do círculo na expressão da aceleração centrípeta.

Solução

Defina a aceleração centrípeta igual à aceleração da gravidade: 9,8 m/s ² =\(\frac{v^{2}}{r}\).

Resolvendo o raio, encontramos

\[r = \frac{(134.1\; m/s)^{2}}{9.8\; m/s^{2}} = 1835\; m = 1.835\; km \ldotp\]

Significância

Para criar uma aceleração maior do que g no piloto, o jato teria que diminuir o raio de sua trajetória circular ou aumentar sua velocidade em sua trajetória existente ou ambos.

Exercício 4.5

Um volante tem um raio de 20,0 cm. Qual é a velocidade de um ponto na borda do volante se ele experimentar uma aceleração centrípeta de 900,0 cm/s ²?

A aceleração centrípeta pode ter uma ampla faixa de valores, dependendo da velocidade e do raio de curvatura do caminho circular. As acelerações centrípetas típicas são apresentadas na Tabela\(\PageIndex{1}\).

Tabela\(\PageIndex{1}\): Acelerações centrípetas típicas
Objeto	Aceleração centrípeta (m/s ² ou fatores de g)
Terra ao redor do sol	5,93 x 10 ^-3
Lua ao redor da Terra	2,73 x 10 ^-3
Satélite em órbita geossíncrona	0,233
Borda externa de um CD durante a reprodução	5,75
Jato em um rolo de barril	(2-3 g)
montanha-russa	(5 g)
Elétron orbitando um próton em um modelo simples de Bohr do átomo	9,0 x 10 ²²

Equações de movimento para movimento circular uniforme

Uma partícula executando movimento circular pode ser descrita por seu vetor de posição\(\vec{r}(t)\). \(\PageIndex{3}\)A figura mostra uma partícula executando movimento circular no sentido anti-horário. Conforme a partícula se move no círculo, seu vetor de posição varre o ângulo\(\theta\) com o eixo x. O vetor que\(\vec{r}(t)\) faz um ângulo\(\theta\) com o eixo x é mostrado com seus componentes ao longo dos eixos x e y. A magnitude do vetor de posição é\(A = |\vec{r}(t)|\) e também é o raio do círculo, de modo que, em termos de seus componentes,

\[\vec{r} (t) = A \cos \omega \hat{i} + A \sin \omega t \hat{j} \ldotp \label{4.28}\]

Aqui,\(\omega\) está uma constante chamada frequência angular da partícula. A frequência angular tem unidades de radianos (rad) por segundo e é simplesmente o número de radianos de medida angular pelos quais a partícula passa por segundo. O ângulo\(θ\) que o vetor de posição tem em qualquer momento específico é\(\omega\) t.

Se\(T\) for o período de movimento, ou o tempo para completar uma revolução (\(2 \pi\, rad\)), então

É mostrado um raio circular r, centrado na origem de um sistema de coordenadas x y. O raio r de t é um vetor da origem até um ponto no círculo e está em um ângulo de teta igual a ômega t em relação à horizontal. O componente x do vetor r é a magnitude de r de t vezes cosseno do ômega t. O componente y do vetor r é a magnitude de r de t vezes seno do ômega t. A circulação é no sentido anti-horário ao redor do círculo. — Figura\(\PageIndex{3}\): O vetor de posição de uma partícula em movimento circular com seus componentes ao longo dos eixos x e y. A partícula se move no sentido anti-horário. Ângulo\(\theta\) é a frequência angular\(\omega\) em radianos por segundo multiplicada por\(t\).

A velocidade e a aceleração podem ser obtidas a partir da função de posição por diferenciação:

\[\vec{v} (t) = \frac{d \vec{r} (t)}{dt} = -A \omega \sin \omega t \hat{i} + A \omega \cos \omega t \hat{j} \ldotp \label{4.29}\]

Pode-se mostrar na Figura\(\PageIndex{3}\) que o vetor de velocidade é tangencial ao círculo na localização da partícula, com magnitude\(\omega\) A. Da mesma forma, o vetor de aceleração é encontrado diferenciando a velocidade:

\[\vec{a} (t) = \frac{d \vec{v} (t)}{dt} = -A \omega^{2} \cos \omega t \hat{i} - A \omega^{2} \sin \omega t \hat{j} \ldotp \label{4.30}\]

A partir dessa equação, vemos que o vetor de aceleração tem magnitude A\(\omega^{2}\) e é direcionado em frente ao vetor de posição, em direção à origem, porque\(\vec{a}\) (t) = −\(\omega^{2} \vec{r}\) (t).

Exemplo\(\PageIndex{2}\): Circular Motion of a Proton

Um próton tem velocidade 5 x 10 ⁶ m/s e está se movendo em um círculo no plano xy do raio r = 0,175 m. Qual é sua posição no plano xy no tempo t = 2,0 x 10 ⁻⁷ s = 200 ns? Em t = 0, a posição do próton é 0,175 m\(\hat{i}\) e ele circula no sentido anti-horário. Esboce a trajetória.

Solução

A partir dos dados fornecidos, o próton tem período e frequência angular:

\[T = \frac{2 \pi r}{v} = \frac{2 \pi (0.175\; m)}{5.0 \times 10^{6}\; m/s} = 2.20 \times 10^{-7}\; s \nonumber \]

\[\omega = \frac{2 \pi}{T} = \frac{2 \pi}{2.20 \times 10^{-7}\; s} = 2.856 \times 10^{7}\; rad/s \ldotp \nonumber \]

A posição da partícula em t = 2,0 x 10 ⁻⁷ s com A = 0,175 m é

\[\begin{align*} \vec{r} (2.0 \times 10^{-7}\; s) & = A \cos \omega (2.0 \times 10^{-7}\; s) \hat{i} + A \sin \omega (2.0 \times 10^{-7}\; s) \hat{j}\; m \\[4pt] & = 0.175 \cos (2.856 \times 10^{7}\; rad/s) (2.0 \times 10^{-7}\; s) \hat{i} + 0.175 \sin (2.856 \times 10^{7}\; rad/s) (2.0 \times 10^{-7}\; s) \hat{j}\; m \\[4pt] & = 0.175 \cos (5.712\; rad) \hat{i} + 0.175 \sin (5.172\; rad) \hat{j}\; m \\ & = 0.147 \hat{i} - 0.095 \hat{j}\; m \ldotp \end{align*}\]

A partir desse resultado, vemos que o próton está localizado um pouco abaixo do eixo x. Isso é mostrado na Figura\(\PageIndex{4}\).

Um gráfico da posição y em função da posição x é mostrado. Tanto x quanto y são medidos em metros e vão de -0,2 a 0,2. Um próton está se movendo em um círculo no sentido anti-horário centrado na origem e é mostrado em 11 momentos diferentes. Em t = 0 s, a partícula está em x = 0,175 m e y = 0. Em t = 200 nanossegundos, a partícula está em uma posição dada pelo vetor 0,147 I hat menos 0,95 j em metros. — Figura\(\PageIndex{4}\): Vetor de posição do próton em\(t = 2.0 \times 10^{−7}\,ms = 200\, ns\). A trajetória do próton é mostrada. O ângulo pelo qual o próton viaja ao longo do círculo é de 5.712 rad, o que é um pouco menos de uma revolução completa.

Significância

Escolhemos a posição inicial da partícula para estar no eixo x. Isso foi completamente arbitrário. Se uma posição inicial diferente fosse dada, teríamos uma posição final diferente em t = 200 ns.

Movimento circular não uniforme

O movimento circular não precisa estar em uma velocidade constante. Uma partícula pode viajar em um círculo e acelerar ou diminuir a velocidade, mostrando uma aceleração na direção do movimento.

Em movimento circular uniforme, a partícula que executa o movimento circular tem uma velocidade constante e o círculo está em um raio fixo. Se a velocidade da partícula também estiver mudando, introduzimos uma aceleração adicional na direção tangencial ao círculo. Essas acelerações ocorrem em um ponto no topo que está mudando sua taxa de rotação ou em qualquer rotor acelerado. Em Vetores de Deslocamento e Velocidade, mostramos que a aceleração centrípeta é a taxa temporal de mudança da direção do vetor de velocidade. Se a velocidade da partícula estiver mudando, ela tem uma aceleração tangencial que é a taxa de variação temporal da magnitude da velocidade:

\[a_{T} = \frac{d |\vec{v}|}{dt} \ldotp \label{4.31}\]

A direção da aceleração tangencial é tangente ao círculo, enquanto a direção da aceleração centrípeta é radialmente para dentro em direção ao centro do círculo. Assim, uma partícula em movimento circular com aceleração tangencial tem uma aceleração total que é a soma vetorial das acelerações centrípeta e tangencial:

\[\vec{a} = \vec{a}_{c} + \vec{a}_{T} \ldotp \label{4.32}\]

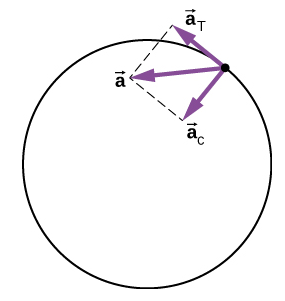
Os vetores de aceleração são mostrados na Figura\(\PageIndex{5}\). Observe que os dois vetores\(\vec{a}_{c}\) de aceleração\(\vec{a}_{T}\) são perpendiculares entre si,\(\vec{a}_{c}\) na direção radial e\(\vec{a}_{T}\) na direção tangencial. O total de\(\vec{a}\) pontos de aceleração em um ângulo entre\(\vec{a}_{c}\)\(\vec{a}_{T}\) e.

A aceleração de uma partícula em um círculo é mostrada junto com seus componentes radiais e tangenciais. A aceleração centrípeta a sub c aponta radialmente para o centro do círculo. A aceleração tangencial de um subT é tangencial ao círculo na posição da partícula. A aceleração total é a soma vetorial das acelerações tangenciais e centrípetas, que são perpendiculares. — Figura\(\PageIndex{5}\): A aceleração centrípeta aponta para o centro do círculo. A aceleração tangencial é tangencial ao círculo na posição da partícula. A aceleração total é a soma vetorial das acelerações tangenciais e centrípetas, que são perpendiculares.

Exemplo\(\PageIndex{3}\): Total Acceleration during Circular Motion

Uma partícula se move em um círculo de raio r = 2,0 m. Durante o intervalo de tempo de t = 1,5 s a t = 4,0 s, sua velocidade varia com o tempo, de acordo com

\[v(t) = c_{1} - \frac{c_{2}}{t^{2}}, c_{1} = 4.0\; m/s, c_{2} = 6.0\; m \cdotp s \ldotp\]

Qual é a aceleração total da partícula em t = 2,0 s?

Estratégia

Recebemos a velocidade da partícula e o raio do círculo, para que possamos calcular facilmente a aceleração centrípeta. A direção da aceleração centrípeta é em direção ao centro do círculo. Determinamos a magnitude da aceleração tangencial tomando a derivada em relação ao tempo de |v (t) | usando a Equação\ ref {4.31} e avaliando-a em t = 2,0 s. Usamos isso e a magnitude da aceleração centrípeta para encontrar a aceleração total.

Solução

A aceleração centrípeta é

\[v(2.0\; s) = \left(4.0 - \dfrac{6.0}{(2.0)^{2}}\right) m/s = 2.5\; m/s \nonumber \]

\[a_{c} = \frac{v^{2}}{r} = \frac{(2.5\; m/s)^{2}}{2.0\; m} = 3.1\; m/s^{2} \nonumber \]

direcionado para o centro do círculo. A aceleração tangencial é

\[a_{T} = \Big| \frac{d \vec{v}}{dt} \Big| = \frac{2 c_{2}}{t^{3}} = \frac{12.0}{(2.0)^{3}} m/s^{2} = 1.5\; m/s^{2} \ldotp \nonumber \]

A aceleração total é

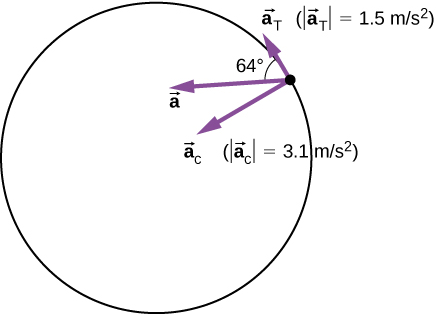
\[|\vec{a}| = \sqrt{3.1^{2} + 1.5^{2}} m/s^{2} = 3.44\; m/s^{2}\]

e\(\theta\) = tan ⁻¹\(\left(\dfrac{3.1}{1.5}\right)\) = 64° da tangente ao círculo. Veja a Figura\(\PageIndex{6}\).

alt="A aceleração de uma partícula em um círculo é mostrada junto com seus componentes radiais e tangenciais. A aceleração centrípeta a sub c aponta radialmente para o centro do círculo e tem magnitude de 3,1 metros por segundo ao quadrado. A aceleração tangencial a sub T é tangencial ao círculo na posição da partícula e tem magnitude de 1,5 metros por segundo ao quadrado. O ângulo entre a aceleração total a e a aceleração tangencial a sub T é de 64 graus.” — Figura\(\PageIndex{6}\): Os vetores de aceleração tangencial e centrípeta. A aceleração líquida\(\vec{a}\) é a soma vetorial das duas acelerações.

Significância

As direções das acelerações centrípetas e tangenciais podem ser descritas de forma mais conveniente em termos de um sistema de coordenadas polares, com vetores unitários nas direções radial e tangencial. Esse sistema de coordenadas, que é usado para movimento ao longo de caminhos curvos, é discutido em detalhes posteriormente no livro.