4.4: Movimento do projétil

Last updated
Save as PDF

Page ID: 185319

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Use o movimento unidimensional em direções perpendiculares para analisar o movimento do projétil.
Calcule o alcance, o tempo de voo e a altura máxima de um projétil que é lançado e impacta uma superfície plana e horizontal.
Encontre o tempo de voo e a velocidade de impacto de um projétil que pousa em uma altura diferente da do lançamento.
Calcule a trajetória de um projétil.

O movimento do projétil é o movimento de um objeto lançado ou projetado no ar, sujeito apenas à aceleração como resultado da gravidade. As aplicações do movimento de projéteis em física e engenharia são inúmeras. Alguns exemplos incluem meteoros que entram na atmosfera da Terra, fogos de artifício e o movimento de qualquer bola nos esportes. Esses objetos são chamados de projéteis e seu caminho é chamado de trajetória. O movimento dos objetos que caem, conforme discutido em Movimento ao longo de uma linha reta, é um tipo simples e unidimensional de movimento de projétil no qual não há movimento horizontal. Nesta seção, consideramos o movimento bidimensional do projétil e nosso tratamento negligencia os efeitos da resistência do ar.

O fato mais importante a lembrar aqui é que os movimentos ao longo dos eixos perpendiculares são independentes e, portanto, podem ser analisados separadamente. Discutimos esse fato em Vetores de Deslocamento e Velocidade, onde vimos que os movimentos verticais e horizontais são independentes. A chave para analisar o movimento bidimensional do projétil é dividi-lo em dois movimentos: um ao longo do eixo horizontal e outro ao longo da vertical. (Essa escolha de eixos é a mais sensata porque a aceleração resultante da gravidade é vertical; portanto, não há aceleração ao longo do eixo horizontal quando a resistência do ar é insignificante.) Como é habitual, chamamos o eixo horizontal de eixo x e o eixo vertical de eixo y. Não é necessário usar essa escolha de eixos; é simplesmente conveniente no caso de aceleração gravitacional. Em outros casos, podemos escolher um conjunto diferente de eixos. A figura$\PageIndex{1}$ ilustra a notação para deslocamento, onde$\vec{s}$ definimos como sendo o deslocamento total,$\vec{x}$ e$\vec{y}$ são seus vetores componentes ao longo dos eixos horizontal e vertical, respectivamente. As magnitudes desses vetores são s, x e y.

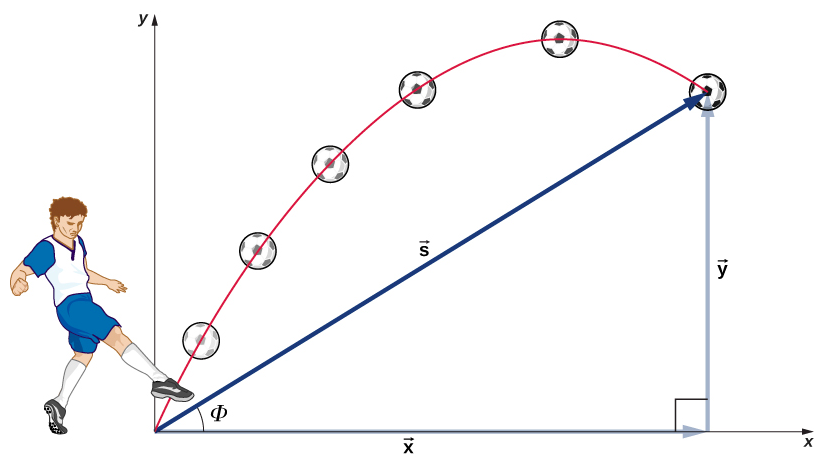
Uma ilustração de um jogador de futebol chutando uma bola. O pé do jogador de futebol está na origem de um sistema de coordenadas x y. A trajetória da bola de futebol e sua localização em 6 instantes no tempo são mostradas. A trajetória é uma parábola. O vetor s é o deslocamento da origem até a posição final da bola de futebol. O vetor s e seus componentes x e y formam um triângulo reto, com s como hipotenusa e um ângulo phi entre o eixo x e s. — Figura$\PageIndex{1}$: O deslocamento total s de uma bola de futebol em um ponto ao longo de seu caminho. O vetor$\vec{s}$ tem componentes$\vec{x}$ e$\vec{y}$ ao longo dos eixos horizontal e vertical. Sua magnitude é s e faz um ângulo$\phi$ com a horizontal.

Para descrever completamente o movimento do projétil, devemos incluir velocidade e aceleração, bem como deslocamento. Devemos encontrar seus componentes ao longo dos eixos x e y. Vamos supor que todas as forças, exceto a gravidade (como resistência do ar e atrito, por exemplo) sejam insignificantes. Definindo a direção positiva para cima, os componentes da aceleração são então muito simples:

\[a_{y} = −g = −9.8\; m/s^{2} (− 32\; ft/s^{2}) \ldotp\]

Como a gravidade é vertical, _x = 0. Se _x = 0, isso significa que a velocidade inicial na direção x é igual à velocidade final na direção x, ou v _x = v _0x. Com essas condições de aceleração e velocidade, podemos escrever a Equação cinemática 4.11 até a Equação 4.18 para movimento em um campo gravitacional uniforme, incluindo o resto das equações cinemáticas para uma aceleração constante do Movimento com Aceleração Constante. As equações cinemáticas para o movimento em um campo gravitacional uniforme se tornam equações cinemáticas com _y = −g, a _x = 0:

Movimento horizontal

\[v_{0x} = v_{x}, \quad x = x_{0} + v_{x} t \label{4.19}\]

Movimento vertical

\[y = y_{0} + \frac{1}{2} (v_{0y} + v_{y})t \label{4.20}\]

\[v_{y} = v_{0y} - gt \label{4.21}\]

\[y = y_{0} + v_{0y} t - \frac{1}{2} g t^{2} \label{4.22}\]

\[v_{y}^{2}= v_{0y}^{2} + 2g(y − y_{0}) \label{4.23}\]

Usando esse conjunto de equações, podemos analisar o movimento do projétil, tendo em mente alguns pontos importantes.

Estratégia de resolução de problemas: movimento de projéteis

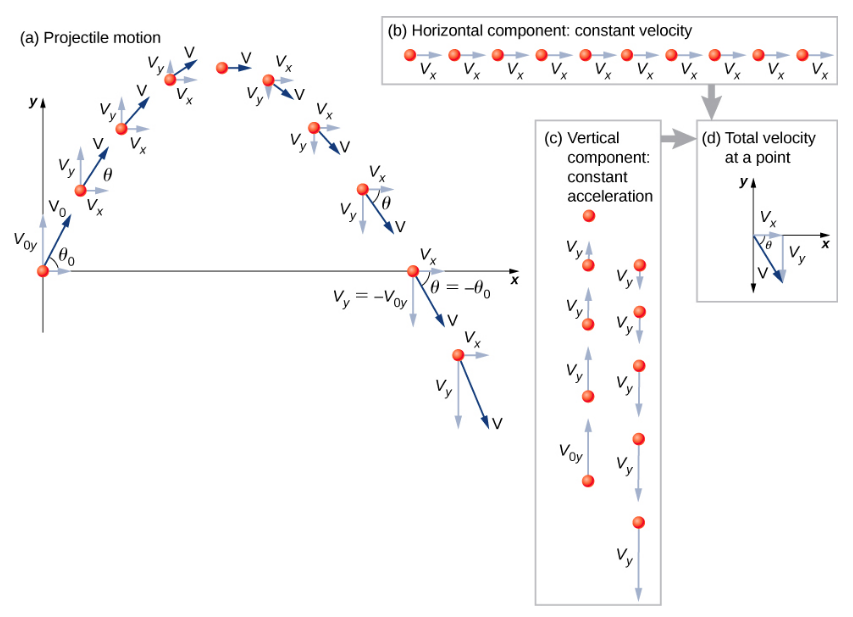
Resolva o movimento em componentes horizontais e verticais ao longo dos eixos x e y. As magnitudes dos componentes de deslocamento$\vec{s}$ ao longo desses eixos são x e y. As magnitudes dos componentes da velocidade$\vec{v}$ são v _x = vcos$\theta$ e v _y = vsin$\theta$, onde v é a magnitude da velocidade e$\theta$ é sua direção em relação a a horizontal, conforme mostrado na Figura$\PageIndex{2}$.
Trate o movimento como dois movimentos unidimensionais independentes: um horizontal e outro vertical. Use as equações cinemáticas para o movimento horizontal e vertical apresentadas anteriormente.
Resolva as incógnitas em dois movimentos separados: um horizontal e outro vertical. Observe que a única variável comum entre os movimentos é o tempo t. Os procedimentos de resolução de problemas aqui são os mesmos da cinemática unidimensional e são ilustrados nos seguintes exemplos resolvidos.
Recombine quantidades nas direções horizontal e vertical para encontrar o deslocamento total$\vec{s}$ e a velocidade$\vec{v}$. Resolva a magnitude e a direção do deslocamento e da velocidade usando $$s =\ sqrt {x^ {2} + y^ {2}}\ ldotp\ quad\ phi =\ tan^ {-1}\ left (\ dfrac {y} {x}\ right),\ quad v =\ sqrt {v_ {x} ^ {2} + v_ {y} ^ {y} ^ 2}}\ ldotp$$onde$\phi$ é a direção do deslocamento$\vec{s}$.

A Figura a mostra as localizações e velocidades de um projétil em um sistema de coordenadas x y em 10 instantes no tempo. Quando o projétil está na origem, ele tem uma velocidade v sub 0 y que forma um ângulo teta sub 0 com a horizontal. A velocidade é mostrada como uma seta azul escura e seus componentes x e y são mostrados como seta azul clara. A posição do projétil segue uma parábola de abertura para baixo, subindo até uma altura máxima, depois de volta para y = 0 e continuando abaixo do eixo x. A velocidade, V, a cada vez forma um ângulo teta que muda com o tempo, e tem x componente V sub x e componente y v sub y. O componente x da velocidade V sub x é o mesmo em todos os momentos. O componente y v sub y aponta para cima, mas fica menor, até que o projétil alcance a altura máxima, onde a velocidade é horizontal e não tem componente y. Depois da altura máxima, a velocidade tem um componente y apontando para baixo e crescendo. Quando o projétil atinge a mesma elevação na descida que tinha na subida, sua velocidade está abaixo da horizontal pelo mesmo ângulo teta em que estava acima da horizontal na subida. Em particular, quando volta a y = 0 na descida, o ângulo entre o vetor v e a horizontal é menos s=teta sub zero e o componente y da velocidade é menos v sub 0 y. A última posição mostrada está abaixo do eixo x, e o componente y da velocidade é maior do que era inicialmente. O gráfico mostra claramente que as distâncias horizontais percorridas em cada um dos intervalos de tempo são iguais, enquanto as distâncias verticais diminuem na subida e aumentam na descida. A Figura b mostra a componente horizontal, velocidade constante. As posições horizontais e os componentes x da velocidade do projétil são mostrados ao longo de uma linha horizontal. As posições são espaçadas uniformemente e os componentes x das velocidades são todos iguais e apontam para a direita. A Figura c mostra a componente vertical, aceleração constante. As posições verticais e os componentes y da velocidade do projétil são mostrados ao longo de uma linha vertical. As posições ficam mais próximas na subida, depois mais afastadas na descida. Os componentes y das velocidades inicialmente apontam para cima, diminuindo em magnitude até que não haja nenhum componente y na velocidade na altura máxima. Após a altura máxima, os componentes y das velocidades apontam para baixo e aumentam de magnitude. A Figura d mostra que colocar os componentes horizontal e vertical das figuras b e c juntos dá a velocidade total em um ponto. A velocidade V tem um componente x de V sub x, tem componente y de V sub y e faz um ângulo de teta com a horizontal. No exemplo mostrado, a velocidade tem um componente y descendente. — Figura$\PageIndex{2}$: (a) Analisamos o movimento bidimensional do projétil dividindo-o em dois movimentos unidimensionais independentes ao longo dos eixos vertical e horizontal. (b) O movimento horizontal é simples, porque a _x = 0 e v _x é uma constante. (c) A velocidade na direção vertical começa a diminuir à medida que o objeto sobe. Em seu ponto mais alto, a velocidade vertical é zero. Quando o objeto cai em direção à Terra novamente, a velocidade vertical aumenta novamente em magnitude, mas aponta na direção oposta à velocidade vertical inicial. (d) Os movimentos x e y são recombinados para dar a velocidade total em qualquer ponto da trajetória.

Exemplo 4.7: Um projétil de fogos de artifício explode bem alto

Durante uma exibição de fogos de artifício, um projétil é lançado no ar com uma velocidade inicial de 70,0 m/s em um ângulo de 75,0° acima da horizontal, conforme ilustrado na Figura$\PageIndex{3}$. O fusível é programado para acender a concha assim que ela atinge seu ponto mais alto acima do solo. (a) Calcule a altura em que a concha explode. (b) Quanto tempo passa entre o lançamento do projétil e a explosão? (c) Qual é o deslocamento horizontal da concha quando ela explode? (d) Qual é o deslocamento total do ponto de lançamento para o ponto mais alto?

A trajetória de um projétil de fogos de artifício desde seu lançamento até seu ponto mais alto é mostrada como a metade esquerda de uma parábola que se abre para baixo em um gráfico de y em função de x. A altura máxima é h = 233 metros e seu deslocamento x nesse momento é x = 125 metros. O vetor de velocidade inicial v sub 0 está para cima e para a direita, tangente à curva de trajetória, e faz com que um ângulo de teta sub 0 seja igual a 75 graus. — Figura$\PageIndex{3}$: A trajetória de um projétil de fogos de artifício. O fusível está configurado para explodir o projétil no ponto mais alto de sua trajetória, que se encontra a uma altura de 233 m e 125 m de distância horizontalmente.

Estratégia

O movimento pode ser dividido em movimentos horizontais e verticais nos quais _x = 0 e _y = −g. Podemos então definir x ₀ e y ₀ como zero e resolver as quantidades desejadas.

Solução

Por “altura”, queremos dizer a altitude ou posição vertical y acima do ponto de partida. O ponto mais alto em qualquer trajetória, chamado ápice, é alcançado quando v _y = 0. Como conhecemos as velocidades inicial e final, bem como a posição inicial, usamos a seguinte equação para encontrar y: $$v_ {y} ^ {2} = v_ {0y} ^ {2} - 2g (y - y_ {0})\ ldotp$$Como y ₀ e v _y são ambos zero, a equação simplifica para $$0 = v_ {0y} ^ {2} - 2gy\ lDotp$$A solução para y dá $$y =\ frac {v_ {0y} ^ {2}} {2g}\ lDotp$$Agora precisamos encontrar v _0y, o componente da velocidade inicial na direção y. É dado por v _0y = v ₀ sin$\theta_{0}$, onde v ₀ é a velocidade inicial de 70,0 m/s e$\theta_{0}$ = 75° é o ângulo inicial. Assim, $$v_ {0y} = v_ {0}\ sin\ theta = (70,0\; m/s)\ sin 75^ {o} = 67,6\; m/s$$e y é $$y =\ frac {(67,6\; m/s) ^ {2}} {2 (9,80\; m/s^ {2})}\ lDotp$Assim, temos $ $y = 233\; m\ lDotp$$Note que, como up é positivo, a velocidade vertical inicial é positiva, assim como a altura máxima, mas a aceleração resulta da gravidade é negativo. Observe também que a altura máxima depende apenas do componente vertical da velocidade inicial, de modo que qualquer projétil com um componente vertical inicial de velocidade de 67,6 m/s atinge uma altura máxima de 233 m (negligenciando a resistência do ar). Os números neste exemplo são razoáveis para grandes fogos de artifício, cujos projéteis atingem essas alturas antes de explodirem. Na prática, a resistência do ar não é completamente desprezível, então a velocidade inicial teria que ser um pouco maior do que a fornecida para atingir a mesma altura.
Como em muitos problemas de física, há mais de uma maneira de resolver o momento em que o projétil atinge seu ponto mais alto. Nesse caso, o método mais fácil é usar v _y = v _0y − gt. Como v _y = 0 no ápice, essa equação reduz $$0 = v_ {0y} - gt$$or $$t =\ frac {v_ {0y}} {g} =\ frac {67.6\; m/s} {9.80\; m/s^ {2}} = 6,90\; s\ lDotp$$ Esse tempo também é razoável para grandes fogos de artifício. Se você conseguir ver o lançamento de fogos de artifício, observe que alguns segundos se passam antes que o projétil exploda. Outra forma de encontrar o tempo é usando y = y ₀ +$\frac{1}{2}$ (v _0y + v _y) t. Isso é deixado para você como um exercício a ser concluído.
Como a resistência do ar é insignificante, _x = 0 e a velocidade horizontal é constante, conforme discutido anteriormente. O deslocamento horizontal é a velocidade horizontal multiplicada pelo tempo, dada por x = x ₀ + v _x t, onde x ₀ é igual a zero. Assim, $$x = v_ {x} t, $$onde v _x é o componente x da velocidade, que é dado por $$v_ {x} = v_ {0}\ cos\ theta = (70.0\; m/s)\ cos 75^ {o} = 18,1\; m/s\ lDotp$$time t para ambos os movimentos é o mesmo, então x é $$x = (18,1\; m/s) (6,90\; s) = 125\; m\ lDOTP$$O movimento horizontal é uma velocidade constante no ausência de resistência do ar. O deslocamento horizontal encontrado aqui pode ser útil para evitar que os fragmentos de fogos de artifício caiam sobre os espectadores. Quando o projétil explode, a resistência do ar tem um efeito importante e muitos fragmentos caem diretamente abaixo.
Os componentes horizontal e vertical do deslocamento acabaram de ser calculados, então tudo o que é necessário aqui é encontrar a magnitude e a direção do deslocamento no ponto mais alto: $$\ vec {s} = 125\ hat {i} + 233\ hat {j} $$$|\ vec {s} | =\ sqrt {125^ {2} + 233^ {2}} = 264\; m$$$$\ theta =\ tan^ {-1}\ left (\ dfrac { 233} {125}\ right) = 61,8^ {o}\ lDotp$$Note que o ângulo do vetor de deslocamento é menor que o ângulo inicial de lançamento. Para ver por que isso acontece, revise a Figura$\PageIndex{1}$, que mostra a curvatura da trajetória em direção ao nível do solo. Ao resolver o Exemplo 4.7 (a), a expressão que encontramos para y é válida para qualquer movimento de projétil quando a resistência do ar é insignificante. Chame a altura máxima y = h. Então, $$h =\ frac {v_ {0y} ^ {2}} {2g}\ lDotp$$Essa equação define a altura máxima de um projétil acima de sua posição de lançamento e depende apenas do componente vertical da velocidade inicial.

Exercício 4.3

Uma rocha é lançada horizontalmente de um penhasco de 100,0 m de altura com uma velocidade de 15,0 m/s. (a) Defina a origem do sistema de coordenadas. (b) Qual equação descreve o movimento horizontal? (c) Quais equações descrevem o movimento vertical? (d) Qual é a velocidade da rocha no ponto de impacto?

Exemplo 4.8: Calculando o movimento do projétil - jogador de tênis

Um tenista vence uma partida no estádio Arthur Ashe e acerta uma bola nas arquibancadas a 30 m/s e em um ângulo de 45° acima da horizontal (Figura$\PageIndex{4}$). Ao descer, a bola é pega por um espectador 10 m acima do ponto em que a bola foi atingida. (a) Calcule o tempo que a bola de tênis leva para chegar ao espectador. (b) Quais são a magnitude e a direção da velocidade da bola no impacto?

Uma ilustração de uma bola de tênis lançada nas arquibancadas. O jogador fica à esquerda das arquibancadas e bate a bola para cima e para a direita em um ângulo de teta igual a 45 graus e velocidade de v sub 0 igual a 30 metros por segundo. A bola atinge um espectador que está sentado 10 metros acima da altura inicial da bola. — Figura$\PageIndex{4}$: A trajetória de uma bola de tênis batendo nas arquibancadas.

Estratégia

Novamente, resolver esse movimento bidimensional em dois movimentos unidimensionais independentes nos permite resolver as quantidades desejadas. O tempo em que um projétil está no ar é governado apenas por seu movimento vertical. Assim, resolvemos para t primeiro. Enquanto a bola sobe e desce verticalmente, o movimento horizontal continua a uma velocidade constante. Este exemplo pede a velocidade final. Assim, recombinamos os resultados verticais e horizontais para obter$\vec{v}$ no tempo final t, determinado na primeira parte do exemplo.

Solução

Enquanto a bola está no ar, ela sobe e depois desce para uma posição final 10,0 m acima de sua altitude inicial. Podemos encontrar o tempo para isso usando a Equação\ ref {4.22}: $$y = y_ {0} + v_ {0y} t -\ frac {1} {2} gt^ {2}\ lDotp$$Se considerarmos a posição inicial y ₀ como zero, a posição final será y = 10 m. A velocidade vertical inicial é o componente vertical da velocidade inicial: $$v_ {0y} = v_ {0}\ sin\ theta_ {0} = (30,0\; m/s)\ sin 45^ {o} = 21,2\; m/s\ lDOTP$$ Substituir y na Equação\ ref {4.22} por y nos dá $$10,0\; m = (21,2\; m/s) t − (4,90\; m/s^ {2}) t^ {2}\ LdotP$$Reorganizar termos dá um equação quadrática em t: $$ (4,90\; m/s^ {2}) t^ {2} − (21,2\; m/s) t + 10,0\; m = 0\ lDotp$$Uso da fórmula quadrática produz t = 3,79 s e t = 0,54 s. Como a bola está a uma altura de 10 m duas vezes durante sua trajetória — uma na subida e outra na descida — tomamos a solução mais longa para o tempo que a bola leva para alcançar o espectador: $$t = 3,79\; s\ lDotp$$O tempo para o movimento do projétil é determinado completamente pelo movimento vertical. Assim, qualquer projétil que tenha uma velocidade vertical inicial de 21,2 m/s e caia 10,0 m acima de sua altitude inicial passa 3,79 s no ar.
Podemos encontrar as velocidades finais horizontais e verticais v _x e v _y com o uso do resultado de (a). Em seguida, podemos combiná-los para encontrar a magnitude do vetor de velocidade total$\vec{v}$ e o ângulo$\theta$ que ele faz com a horizontal. Como v _x é constante, podemos resolvê-lo em qualquer local horizontal. Escolhemos o ponto de partida porque conhecemos a velocidade inicial e o ângulo inicial. Portanto, $$v_ {x} = v_ {0}\ cos\ theta_ {0} = (30\; m/s)\ cos 45^ {o} = 21,2\; m/s\ lDotp$$A velocidade vertical final é dada pela Equação\ ref {4.21}: $$v_ {y} = v_ {0y} − gt\ ldotp$$since$v_{0y}$ foi encontrada em parte (a) para ser 21,2 m/s, temos $$v_ {y} = 21,2\; m/s − (9,8\; m/s^ {2}) (3,79 s) = −15,9\; m/s\ ldotp$$ A magnitude da velocidade final$\vec{v}$ é $$v =\ sqrt {v_ {x} ^ {2} + v_ {y} ^ {2}} =\ sqrt {(21,2\; m/s) ^ {2} + (-15,9\; m/s) ^ {2}} = 26,5\; m/s\ lDotp$$A direção$\theta_{v}$ é encontrada usando a tangente inversa: $$\ theta_ {v} =\ tan^ {-1}\ left (\ dfrac {v_ {y}} {v_ {x}}\ direita) =\ tan^ {-1}\ esquerda (\ dfrac {21,2} {-15,9}\ direita) = -53.1^ {o}\ ldotp$$

Significância

Conforme mencionado anteriormente, o tempo de movimento do projétil é determinado completamente pelo movimento vertical. Assim, qualquer projétil que tenha uma velocidade vertical inicial de 21,2 m/s e caia 10,0 m acima de sua altitude inicial passa 3,79 s no ar.
O ângulo negativo significa que a velocidade está 53,1° abaixo da horizontal no ponto de impacto. Esse resultado é consistente com o fato de que a bola está impactando em um ponto do outro lado do ápice da trajetória e, portanto, tem um componente y negativo da velocidade. A magnitude da velocidade é menor do que a magnitude da velocidade inicial que esperamos, pois está impactando 10,0 m acima da elevação do lançamento.

Tempo de voo, trajetória e alcance

Interessantes são o tempo de voo, a trajetória e o alcance de um projétil lançado em uma superfície horizontal plana e impactando na mesma superfície. Nesse caso, as equações cinemáticas fornecem expressões úteis para essas quantidades, que são derivadas nas seções a seguir.

Hora do voo

Podemos resolver o tempo de voo de um projétil que é lançado e impacta em uma superfície horizontal plana realizando algumas manipulações das equações cinemáticas. Observamos que a posição e o deslocamento em y devem ser zero no lançamento e no impacto em uma superfície uniforme. Assim, definimos o deslocamento em y igual a zero e encontramos

\[y − y_{0} = v_{0y} t − \frac{1}{2} gt^{2} = (v_{0} \sin \theta_{0})t − \frac{1}{2} gt^{2} = 0 \ldotp\]

Fatorando, nós temos

\[t \left(v_{0} \sin \theta_{0} - \dfrac{gt}{2}\right) = 0 \ldotp\]

Resolver para t nos dá

\[T_{tof} = \frac{2(v_{0} \sin \theta_{0})}{g} \ldotp \label{4.24}\]

Este é o tempo de voo de um projétil lançado e impactado em uma superfície plana horizontal. A equação\ ref {4.24} não se aplica quando o projétil cai em uma elevação diferente da que foi lançado, como vimos no Exemplo 4.8 do tenista batendo a bola nas arquibancadas. A outra solução, t = 0, corresponde ao tempo de lançamento. O tempo de voo é linearmente proporcional à velocidade inicial na direção y e inversamente proporcional a g. Assim, na Lua, onde a gravidade é um sexto da da Terra, um projétil lançado com a mesma velocidade da Terra estaria no ar seis vezes mais longo.

Trajetória

A trajetória de um projétil pode ser encontrada eliminando a variável de tempo t das equações cinemáticas para t arbitrário e resolvendo para y (x). Tomamos x ₀ = y ₀ = 0 para que o projétil seja lançado da origem. A equação cinemática para x fornece

\[x = v_{0x}t \Rightarrow t = \frac{x}{v_{0x}} = \frac{x}{v_{0} \cos \theta_{0}} \ldotp\]

Substituindo a expressão por t na equação pela posição y = (v ₀ sin$\theta_{0}$) t −$\frac{1}{2}$ gt ² dá

\[y = (v_{0} \sin \theta_{0}) \left(\dfrac{x}{v_{0} \cos \theta_{0}}\right) - \frac{1}{2} g \left(\dfrac{x}{v_{0} \cos \theta_{0}}\right)^{2} \ldotp\]

Reorganizando os termos, temos

\[y = (\tan \theta_{0})x - \Big[ \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \Big] x^{2} \ldotp \label{4.25}\]

Essa equação de trajetória tem a forma y = ax + bx ², que é uma equação de uma parábola com coeficientes

\[a = \tan \theta_{0}, \quad b = - \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \ldotp\]

Alcance

A partir da equação da trajetória, também podemos encontrar o alcance ou a distância horizontal percorrida pelo projétil. Equação de fatoração\ ref {4,25}, temos

\[y = x \Big[ \tan \theta_{0} - \frac{g}{2(v_{0} \cos \theta_{0})^{2}} x \Big] \ldotp\]

A posição y é zero tanto para o ponto de lançamento quanto para o ponto de impacto, já que estamos considerando novamente apenas uma superfície horizontal plana. Definir y = 0 nesta equação fornece soluções x = 0, correspondentes ao ponto de lançamento, e

\[x = \frac{2 v_{0}^{2} \sin \theta_{0} \cos \theta_{0}}{g} ,\]

correspondente ao ponto de impacto. Usando a identidade trigonométrica 2sin$\theta$ cos$\theta$ = sin2$\theta$ e definindo x = R para alcance, encontramos

\[R = \frac{v_{0}^{2} \sin 2 \theta_{0}}{g} \ldotp \label{4.26}\]

Observe particularmente que a Equação\ ref {4.26} é válida somente para lançamento e impacto em uma superfície horizontal. Vemos que o alcance é diretamente proporcional ao quadrado da velocidade inicial v ₀ e sin ²$\theta_{0}$, e é inversamente proporcional à aceleração da gravidade. Assim, na Lua, o alcance seria seis vezes maior do que na Terra para a mesma velocidade inicial. Além disso, vemos pelo fator sin ²$\theta_{0}$ que o alcance é máximo em 45°. Esses resultados são mostrados na Figura$\PageIndex{5}$. Em (a) vemos que quanto maior a velocidade inicial, maior o alcance. Em (b), vemos que o alcance é máximo em 45°. Isso é verdade apenas para condições que negligenciam a resistência do ar. Se a resistência do ar for considerada, o ângulo máximo é um pouco menor. É interessante que o mesmo alcance seja encontrado para dois ângulos iniciais de lançamento que somam 90°. O projétil lançado com o ângulo menor tem um ápice menor do que o ângulo mais alto, mas ambos têm o mesmo alcance.

A Figura a mostra as trajetórias dos projéteis lançados no mesmo ângulo inicial de 45 graus acima da horizontal e diferentes velocidades iniciais. As trajetórias são mostradas do lançamento ao pouso na elevação inicial. Em laranja está a trajetória de 30 metros por segundo, dando um alcance R (distância do lançamento ao pouso) de 91,8 m. Em roxo está a trajetória de 40 metros por segundo, dando um alcance R de 163 m. Em azul está a trajetória de 50 metros por segundo, dando um alcance R de 255 m. A altura máxima do projétil aumenta com a velocidade inicial. A Figura b mostra as trajetórias dos projéteis lançados na mesma velocidade inicial de 50 metros por segundo e diferentes ângulos de lançamento. As trajetórias são mostradas do lançamento ao pouso na elevação inicial. Em laranja está a trajetória de um ângulo de 15 graus acima da horizontal, dando um alcance R de 128 m. Em roxo é a trajetória para um ângulo de 45 graus acima da horizontal, dando um alcance R de 255 m. Em azul é a trajetória para um ângulo de 75 graus acima da horizontal, dando um alcance R de 128 m, o o mesmo que para a trajetória de 15 graus. A altura máxima aumenta com o ângulo de lançamento. — Figura$\PageIndex{5}$: Trajetórias de projéteis em terreno nivelado. (a) Quanto maior a velocidade inicial v ₀, maior a faixa para um determinado ângulo inicial. (b) O efeito do ângulo inicial (\ theta_ {0}\) no alcance de um projétil com uma determinada velocidade inicial. Observe que o intervalo é o mesmo para ângulos iniciais de 15° e 75°, embora as alturas máximas desses caminhos sejam diferentes.

Exemplo 4.9: Comparando tacadas de golfe

Um jogador de golfe se encontra em duas situações diferentes em buracos diferentes. No segundo buraco, ele está a 120 m do green e quer acertar a bola a 90 m e deixá-la correr para o green. Ele inclina o chute para baixo em relação ao chão a 30° em relação à horizontal para deixar a bola rolar após o impacto. No quarto buraco, ele está a 90 m do green e quer deixar a bola cair com um mínimo de rolamento após o impacto. Aqui, ele inclina o tiro a 70° em relação à horizontal para minimizar o rolamento após o impacto. Ambos os tiros são atingidos e impactados em uma superfície nivelada. (a) Qual é a velocidade inicial da bola no segundo buraco? (b) Qual é a velocidade inicial da bola no quarto buraco? (c) Escreva a equação da trajetória para ambos os casos. (d) Representar graficamente as trajetórias.

Estratégia

Vemos que a equação de alcance tem a velocidade e o ângulo iniciais, então podemos resolver a velocidade inicial para (a) e (b). Quando temos a velocidade inicial, podemos usar esse valor para escrever a equação da trajetória.

Solução

$$R =\ frac {v_ {0} ^ {2}\ sin 2\ theta_ {0}} {g}\ Rightarrow v_ {0} =\ sqrt {\ dfrac {Rg} {\ sin 2\ theta_ {0}}} =\ sqrt {\ dfrac {(90,0\; m) (9,8\; m/s^ {2})} {\ sin (2 (30^ {o}))}} = 31,9\; m/s$$
$$R =\ frac {v_ {0} ^ {2}\ sin 2\ theta_ {0}} {g}\ Rightarrow v_ {0} =\ sqrt {\ dfrac {Rg} {\ sin 2\ theta_ {0}}} =\ sqrt {\ dfrac {(90,0\; m) (9,8\; m/s^ {2})} {\ sin (2 (70^ {o}))}} = 37,0\; m/s$$
$$y = x\ Big [\ tan\ theta_ {0} -\ frac {g} {2 (v_ {0}\ cos\ theta_ {0}) ^ {2}} x\ Grande] $$Segundo buraco: $$y = x\ Grande [\ tan 30^ {o} -\ frac {9.8\; m/s^ {2}} {2 [(31,9\; m/s) (\ cos 30^ {o})] ^ {2}} x\ Big] = 0,58x - 0,0064x^ {2} $$Quarto buraco: $$y = x\ Grande [\ tan 70^ {o} -\ frac {9,8\; m/s^ {2}} {2 [(37,0\; m/s) (\ cos 70^ {o})] ^ {2} x\ Grande] = 2 .75x - 0,0306x^ {2} $$
Usando um utilitário gráfico, podemos comparar as duas trajetórias, mostradas na Figura$\PageIndex{6}$.

Duas funções parabólicas são mostradas. O alcance para ambas as trajetórias é de 90 metros. Um tiro viaja muito mais alto que o outro. O tiro mais alto tem uma velocidade inicial de 37 metros por segundo e um ângulo de 70 graus. O tiro mais baixo tem uma velocidade inicial de 31,9 metros por segundo e um ângulo de 30 graus. — Figura$\PageIndex{6}$: Duas trajetórias de uma bola de golfe com alcance de 90 m. Os pontos de impacto de ambas estão no mesmo nível do ponto de lançamento.

Significância

A velocidade inicial do tiro a 70° é maior do que a velocidade inicial do tiro a 30°. Observe na Figura$\PageIndex{6}$ que dois projéteis lançados na mesma velocidade, mas em ângulos diferentes, têm o mesmo alcance se os ângulos de lançamento aumentarem 90°. Os ângulos de lançamento neste exemplo se somam para dar um número maior que 90°. Assim, o tiro a 70° deve ter uma velocidade de lançamento maior para chegar a 90 m, caso contrário, ele pousaria a uma distância menor.

Exercício 4.4

Se as duas tacadas de golfe no Exemplo 4.9 fossem lançadas na mesma velocidade, qual tiro teria o maior alcance?

Quando falamos do alcance de um projétil em terreno nivelado, assumimos que R é muito pequeno em comparação com a circunferência da Terra. Se, no entanto, o alcance for grande, a Terra se curva abaixo do projétil e a aceleração resultante da gravidade muda de direção ao longo do caminho. O alcance é maior do que o previsto pela equação de alcance dada anteriormente porque o projétil tem mais a cair do que cairia em terreno plano, conforme mostrado na Figura$\PageIndex{7}$, que é baseado em um desenho no Principia de Newton. Se a velocidade inicial for grande o suficiente, o projétil entra em órbita. A superfície da Terra cai 5 m a cada 8000 m. Em 1 s, um objeto cai 5 m sem resistência ao ar. Assim, se um objeto receber uma velocidade horizontal de 8000 m/s (ou 18.000 mi/h) perto da superfície da Terra, ele entrará em órbita ao redor do planeta porque a superfície se afasta continuamente do objeto. Essa é aproximadamente a velocidade do ônibus espacial em uma órbita terrestre baixa quando estava operacional, ou de qualquer satélite em uma órbita terrestre baixa. Esses e outros aspectos do movimento orbital, como a rotação da Terra, são cobertos em maior profundidade pela Gravitação.

A figura mostra um desenho da terra com uma torre alta no pólo norte e uma seta horizontal chamada v 0 apontando para a direita. 5 trajetórias que começam no topo da torre são mostradas. O primeiro chega à terra perto da torre. O segundo alcança a terra mais longe da torre e o terceiro ainda mais longe. A quarta trajetória atinge a Terra no equador e é tangente à superfície no equador. A quinta trajetória é um círculo concêntrico com a terra. — Figura$\PageIndex{7}$: Projétil para satélite. Em cada caso mostrado aqui, um projétil é lançado de uma torre muito alta para evitar a resistência do ar. Com o aumento da velocidade inicial, o alcance aumenta e se torna maior do que seria em um terreno plano porque a Terra se curva abaixo de seu caminho. Com uma velocidade de 8000 m/s, a órbita é alcançada.

Simulação

Em PhET Explorations: Projectile Motion, aprenda sobre o movimento do projétil em termos do ângulo de lançamento e da velocidade inicial.