2.5: Sistemas de coordenadas e componentes de um vetor (Parte 2)
- Page ID
- 184779
Coordenadas polares
Para descrever a localização de pontos ou vetores em um plano, precisamos de duas direções ortogonais. No sistema de coordenadas cartesianas, essas direções são dadas por vetores unitários\(\hat{i}\) e\(\hat{j}\) ao longo do eixo x e do eixo y, respectivamente. O sistema de coordenadas cartesiano é muito conveniente para descrever deslocamentos e velocidades de objetos e as forças que atuam sobre eles. No entanto, isso se torna complicado quando precisamos descrever a rotação dos objetos. Ao descrever a rotação, geralmente trabalhamos no sistema de coordenadas polares.
No sistema de coordenadas polares, a localização do ponto P em um plano é dada por duas coordenadas polares (Figura\(\PageIndex{1}\)). A primeira coordenada polar é a coordenada radial r, que é a distância do ponto P da origem. A segunda coordenada polar é um ângulo\(\varphi\) que o vetor radial faz com alguma direção escolhida, geralmente a direção x positiva. Nas coordenadas polares, os ângulos são medidos em radianos ou rads. O vetor radial é anexado na origem e aponta para longe da origem até o ponto P. Essa direção radial é descrita por um vetor radial unitário\(\hat{r}\). O segundo vetor unitário\(\hat{t}\) é um vetor ortogonal à direção radial\(\hat{r}\). A\(\hat{t}\) direção positiva + indica como o ângulo\(\varphi\) muda no sentido anti-horário. Dessa forma, um ponto P que tem coordenadas (x, y) no sistema retangular pode ser descrito de forma equivalente no sistema de coordenadas polares pelas duas coordenadas polares (r,\(\varphi\)). A equação 2.4.13 é válida para qualquer vetor, então podemos usá-la para expressar as coordenadas x e y do vetor\(\vec{r}\). Dessa forma, obtemos a conexão entre as coordenadas polares e as coordenadas retangulares do ponto P:
\[ \begin{cases} x = r \cos \varphi \\ y = r \sin \varphi \end{cases} \ldotp \label{2.18}\]
Um caçador de tesouros encontra uma moeda de prata em um local a 20,0 m de distância de um poço seco na direção 20° ao norte do leste e encontra uma moeda de ouro em um local a 10,0 m de distância do poço, na direção 20° ao norte de oeste. Quais são as coordenadas polares e retangulares dessas descobertas em relação ao poço?
Estratégia
O poço marca a origem do sistema de coordenadas e o leste é a direção+x. Identificamos distâncias radiais dos locais até a origem, que são r S = 20,0 m (para a moeda de prata) e r G = 10,0 m (para a moeda de ouro). Para encontrar as coordenadas angulares, convertemos 20° em radianos: 20° =\(\frac{\pi\; 20}{180}\) =\(\frac{\pi}{9}\). Usamos a Equação\ ref {2.18} para encontrar as coordenadas x e y das moedas.
Solução
A coordenada angular da moeda de prata é\(\varphi_{S}\) =\(\frac{\pi}{9}\), enquanto a coordenada angular da moeda de ouro é\(\varphi_{G}\) =\(\pi\) −\(\frac{\pi}{9}\) =\(\frac{8 \pi}{9}\). Portanto, as coordenadas polares da moeda de prata são (r S,\(\varphi_{S}\)) = (20,0 m\(\frac{\pi}{9}\)) e as da moeda de ouro são (r G,\(\varphi_{G}\)) = (10,0 m,\ frac {8\ pi} {9}\)). Substituímos essas coordenadas na Equação\ ref {2.18} para obter coordenadas retangulares. Para a moeda de ouro, as coordenadas são
\[ \begin{cases} x_{G} = r_{G} \cos \varphi_{G} = (10.0\; m) \cos \frac{8 \pi}{9} = -9.4\; m \\ y_{G} = r_{G} \sin \varphi_{G} = (10.0\; m) \sin \frac{8 \pi}{9} = 3.4\; m \end{cases} \Rightarrow (x_{G}, y_{G}) = (-9.4\; m, 3.4\; m) \ldotp\]
Para a moeda de prata, as coordenadas são
\[ \begin{cases} x_{S} = r_{S} \cos \varphi_{S} = (20.0\; m) \cos \frac{\pi}{9} = 18.9\; m \\ y_{S} = r_{S} \sin \varphi_{S} = (20.0\; m) \sin \frac{\pi}{9} = 6.8\; m \end{cases} \Rightarrow (x_{S}, y_{S}) = (18.9\; m, 6.8\; m) \ldotp\]
Vetores em três dimensões
Para especificar a localização de um ponto no espaço, precisamos de três coordenadas (x, y, z), onde as coordenadas x e y especificam localizações em um plano e a coordenada z fornece posições verticais acima ou abaixo do plano. O espaço tridimensional tem três direções ortogonais, então não precisamos de dois, mas três vetores unitários para definir um sistema de coordenadas tridimensional. No sistema de coordenadas cartesianas, os dois primeiros vetores unitários são o vetor unitário do eixo x\(\hat{i}\) e o vetor unitário do eixo\(\hat{j}\) y. O terceiro vetor unitário\(\hat{k}\) é a direção do eixo z (Figura\(\PageIndex{2}\)). A ordem na qual os eixos são rotulados, que é a ordem na qual os três vetores unitários aparecem, é importante porque define a orientação do sistema de coordenadas. A ordem x-y-z, que é equivalente à ordem\(\hat{i}\) -\(\hat{j}\) -\(\hat{k}\), define o sistema de coordenadas padrão da mão direita (orientação positiva).
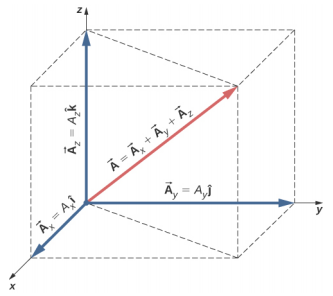
No espaço tridimensional, o vetor\(\vec{A}\) tem três componentes vetoriais: o componente x\(\vec{A}_{x}\) = A x\(\hat{i}\), que é a parte do vetor\(\vec{A}\) ao longo do eixo x; o componente y\(\vec{A}_{y}\) = A y\(\hat{j}\), que é a parte do\(\vec{A}\) ao longo do y- eixo; e o componente z\(\vec{A}_{z}\) = A z\(\hat{k}\), que é a parte do vetor ao longo do eixo z. Um vetor no espaço tridimensional é a soma vetorial de seus três componentes vetoriais (Figura\(\PageIndex{3}\)):
\[\vec{A} = A_{x} \hat{i} + A_{y} \hat{j} + A_{z} \hat{k} \ldotp \label{2.19}\]
Se soubermos as coordenadas de sua origem b (x b, y b, z b) e de sua extremidade e (x e y e, z e), seus componentes escalares são obtidos considerando suas diferenças: A x e A y são dados por
\[ \begin{cases} A_{x} = x_{e} - x_{b} \nonumber \\ A_{y} = y_{e} - y_{b} \ldotp \nonumber \end{cases} \]
e o componente z é dado por
\[A_{z} = z_{e} - z_{b} \ldotp \label{2.20}\]
A magnitude A é obtida generalizando a Equação 2.4.8 para três dimensões:
\[A = \sqrt{A_{x}^{2} + A_{y}^{2} + A_{z}^{2}} \ldotp \label{2.21}\]
Essa expressão para a magnitude vetorial vem da aplicação do teorema de Pitágoras duas vezes. Como visto na Figura\(\PageIndex{3}\), a diagonal no plano xy tem comprimento\(\sqrt{A_{x}^{2} + A_{y}^{2}}\) e seu quadrado se soma ao quadrado A z 2 para dar A 2. Observe que quando o componente z é zero, o vetor fica inteiramente no plano xy e sua descrição é reduzida para duas dimensões.
Durante a decolagem do IAI Heron (Figura\(\PageIndex{4}\)), sua posição em relação a uma torre de controle é de 100 m acima do solo, 300 m a leste e 200 m ao norte. Um minuto depois, sua posição é de 250 m acima do solo, 1200 m para o leste e 2100 m para o norte. Qual é o vetor de deslocamento do drone em relação à torre de controle? Qual é a magnitude de seu vetor de deslocamento?
Estratégia
Tomamos a origem do sistema de coordenadas cartesianas como a torre de controle. A direção do eixo +x é dada pelo vetor unitário\(\hat{i}\) a leste, a direção do eixo +y é dada pelo vetor\(\hat{j}\) unitário ao norte e a direção do eixo +z é dada pelo vetor unitário\(\hat{k}\), que aponta para cima do solo. A primeira posição do drone é a origem (ou, equivalentemente, o início) do vetor de deslocamento e sua segunda posição é o final do vetor de deslocamento.
Solução
Identificamos b (300,0 m, 200,0 m, 100,0 m) e e (480,0 m, 370,0 m, 250,0 m) e usamos a Equação 2.4.4 e a Equação\ ref {2.20} para encontrar os componentes escalares do vetor de deslocamento do drone:
\[ \begin{cases} D_{x} = x_{e} - x_{b} = 1200.0\; m - 300.0\; m = 900.0\; m,\\ D_{y} =y_{e} - y_{b} = 2100.0\; m - 200.0\; m = 1900.0\; m, \\ D_{z} =z_{e} - z_{b} = 250.0\; m - 100.0\; m = 150\; m \ldotp \end{cases}\]
Substituímos esses componentes na Equação\ ref {2.19} para encontrar o vetor de deslocamento:
\[\vec{D} = D_{x}\; \hat{i} + D_{y}\; \hat{j} + D_{z}\; \hat{k} = 900.0\; \hat{i} + 1900.0\; \hat{j} + 150.0\; \hat{k} = (0.90\; \hat{i} + 1.90\; \hat{j} + 0.15\; \hat{k})\; km \ldotp\]
Substituímos na Equação\ ref {2.21} para encontrar a magnitude do deslocamento:
\[D = \sqrt{D_{x}^{2} + D_{y}^{2} + D_{z}^{2}} = \sqrt{(0.90\; km)^{2} + (1.90\; km)^{2} + (0.15\; km)^{2}} = 4.44\; km \ldotp\]
Se o vetor de velocidade média do drone no deslocamento no Exemplo 2.7 for\(\vec{u}\) = (15,0\(\hat{i}\) + 31,7\(\hat{j}\) + 2,5\(\hat{k}\)) m/s, qual é a magnitude do vetor de velocidade do drone?


