2.3: Escalares e vetores (Parte 2)

Last updated
Save as PDF

Page ID: 184809

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Exemplo\(\PageIndex{1}\): A Ladybug Walker

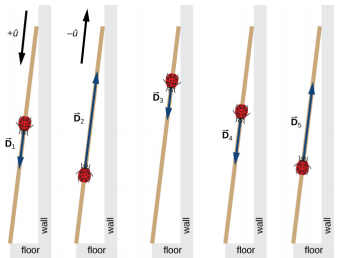
Um longo bastão de medição encosta-se a uma parede em um laboratório de física com sua extremidade de 200 cm no chão. Uma joaninha pousa na marca de 100 cm e rasteja aleatoriamente ao longo do bastão. Ele primeiro caminha 15 cm em direção ao chão, depois caminha 56 cm em direção à parede e depois caminha 3 cm em direção ao chão novamente. Depois de uma breve parada, ele continua por 25 cm em direção ao chão e, novamente, sobe 19 cm em direção à parede antes de descansar completamente (Figura\(\PageIndex{1}\)). Encontre o vetor de seu deslocamento total e sua posição final de repouso no bastão.

Estratégia

Se escolhermos a direção ao longo do bastão em direção ao chão como a direção do vetor unitário\(\hat{u}\), então a direção em direção ao chão é\(+ \hat{u}\) e a direção em direção à parede é\(−\hat{u}\). A joaninha faz um total de cinco deslocamentos:

\[ \begin{align*} \vec{D}_{1} &= (15\; cm)( + \hat{u}), \\[4pt] \vec{D}_{2} &= (56\; cm)( - \hat{u}), \\[4pt] \vec{D}_{3} &= (3\; cm)( + \hat{u}), \\[4pt] \vec{D}_{4} &= (25\; cm)( + \hat{u}), \; and \\[4pt] \vec{D}_{5} &= (19\; cm)( - \hat{u}) \ldotp \end{align*}\]

O deslocamento total\(\vec{D}\) é o resultado de todos os seus vetores de deslocamento.

Cinco ilustrações de uma joaninha em uma régua encostada na parede. A direção do chapéu +u é em direção ao chão, paralela à régua, e a direção do chapéu -u está acima ao longo da régua. Na primeira ilustração, a joaninha está localizada perto do meio da régua e o vetor D sub 1 aponta abaixo da régua. Na segunda ilustração, a joaninha está localizada abaixo, onde a cabeça do vetor D sub 1 está na primeira ilustração e o vetor D sub 2 aponta acima da régua. Na terceira ilustração, a joaninha está localizada mais acima, onde a cabeça do vetor D sub 2 está na segunda ilustração e o vetor D sub 3 pontos abaixo da régua. Na quarta ilustração, a joaninha está localizada abaixo, onde a cabeça do vetor D sub 3 está na terceira ilustração e o vetor D sub 4 pontos abaixo da régua. Na quinta ilustração, a joaninha está localizada abaixo, onde a cabeça do vetor D sub 4 está na quarta ilustração e o vetor D sub 5 aponta acima da régua. — Figura\(\PageIndex{1}\): Cinco deslocamentos da joaninha. Observe que neste desenho esquemático, as magnitudes dos deslocamentos não são desenhadas em escala. (crédito: modificação da obra de “Persian Poet Gal” /Wikimedia Commons)

Solução

A resultante de todos os vetores de deslocamento é

\[ \begin{align*} \vec{D} &= \vec{D}_{1} + \vec{D}_{2} + \vec{D}_{3} + \vec{D}_{4} + \vec{D}_{5} \\[4pt] &= (15\; cm)( + \hat{u} ) + (56\; cm)( −\hat{u} ) + (3\; cm)( + \hat{u} ) + (25\; cm)( + \hat{u}) + (19\; cm)( − \hat{u}) \\[4pt] &= (15 − 56 + 3 + 25 − 19) cm\; \hat{u} \\[4pt] &= −32\; cm\; \hat{u} \ldotp \end{align*}\]

Neste cálculo, usamos a lei distributiva dada pela Equação 2.2.9. O resultado mostra que o vetor de deslocamento total aponta para longe da marca de 100 cm (local de pouso inicial) em direção à extremidade do medidor que toca a parede. A extremidade que toca a parede está marcada com 0 cm, então a posição final da joaninha está na marca (100 - 32) cm = 68 cm.

Exercício 2.2

Um mergulhador de cavernas entra em um longo túnel subaquático. Quando seu deslocamento em relação ao ponto de entrada é de 20 m, ela acidentalmente derruba a câmera, mas não percebe que ela está faltando até que esteja cerca de 6 m mais longe no túnel. Ela nada para trás 10 m, mas não consegue encontrar a câmera, então ela decide terminar o mergulho. A que distância ela está do ponto de entrada? Tomando a direção positiva para fora do túnel, qual é o vetor de deslocamento dela em relação ao ponto de entrada?

Álgebra de vetores em duas dimensões

Quando os vetores estão em um plano, ou seja, quando estão em duas dimensões, eles podem ser multiplicados por escalares, adicionados a outros vetores ou subtraídos de outros vetores de acordo com as leis gerais expressas pela Equação 2.2.1, Equação 2.2.2, Equação 2.2.7 e Equação 2.2.8. No entanto, a regra de adição para dois vetores em um plano se torna mais complicada do que a regra para adição de vetores em uma dimensão. Temos que usar as leis da geometria para construir vetores resultantes, seguidas pela trigonometria para encontrar magnitudes e direções vetoriais. Essa abordagem geométrica é comumente usada na navegação (Figura\(\PageIndex{2}\)). Nesta seção, precisamos ter em mãos duas réguas, um triângulo, um transferidor, um lápis e uma borracha para desenhar vetores em escala por construções geométricas.

Uma fotografia de alguém medindo a distância em um mapa usando pinças e uma régua. — Figura\(\PageIndex{2}\): Na navegação, as leis da geometria são usadas para desenhar os deslocamentos resultantes em mapas náuticos.

Para uma construção geométrica da soma de dois vetores em um plano, seguimos a regra do paralelogramo. Suponha dois vetores\(\vec{A}\) e\(\vec{B}\) esteja nas posições arbitrárias mostradas na Figura\(\PageIndex{3}\). Traduza qualquer um deles em paralelo ao início do outro vetor, para que, após a tradução, os dois vetores tenham suas origens no mesmo ponto. Agora, no final do vetor,\(\vec{A}\) desenhamos uma linha paralela ao vetor\(\vec{B}\) e, no final do vetor,\(\vec{B}\) desenhamos uma linha paralela ao vetor\(\vec{A}\) (as linhas tracejadas na Figura\(\PageIndex{3}\)). Dessa forma, obtemos um paralelogramo. Da origem dos dois vetores, desenhamos uma diagonal que é a resultante\(\vec{R}\) dos dois vetores:\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) (Figura\(\PageIndex{3a}\)). A outra diagonal desse paralelogramo é a diferença vetorial dos dois vetores\(\vec{D}\) =\(\vec{A}\) −\(\vec{B}\), conforme mostrado na Figura\(\PageIndex{3b}\). Observe que o final do vetor de diferença é colocado no final do vetor\(\vec{A}\).

O método do paralelogramo para adicionar vetores é ilustrado. Na figura a, os vetores A e B são mostrados. O vetor A aponta para a direita e para baixo e o vetor B aponta para a direita e para cima. Os vetores A e B são então mostrados como setas sólidas com suas caudas juntas e suas direções como antes. Uma linha tracejada paralela ao vetor A, mas deslocada para começar na cabeça de B, é mostrada. Uma segunda linha tracejada, paralela a B e começando na cabeça de A também é mostrada. Os vetores A e B e as duas linhas tracejadas formam um paralelogramo. Um terceiro vetor, denominado vetor R = vetor A mais vetor B, é exibido. A cauda do vetor R está nas caudas dos vetores A e B, e a cabeça do vetor R é onde as linhas tracejadas se encontram, diagonalmente através do paralelogramo. Observamos que a magnitude de R não é igual à magnitude de A mais a magnitude de B. Na figura b, os vetores A e menos B são mostrados. O vetor menos B é o vetor B da parte a, girado 180 graus. O vetor A aponta para a direita e para baixo e o vetor menos B pontos para a esquerda e para baixo. Os vetores A e B são então mostrados como setas sólidas com suas caudas juntas e suas direções como antes. Uma linha tracejada paralela ao vetor A, mas deslocada para começar na cabeça de B, é mostrada. Uma segunda linha tracejada, paralela a B e começando na cabeça de A também é mostrada. Os vetores A e B e as duas linhas tracejadas formam um paralelogramo. Um terceiro vetor, denominado vetor D, é exibido. A cauda do vetor D está na cabeça do vetor B, e a cabeça do vetor D está na cabeça do vetor A, diagonalmente através do paralelogramo. Observamos que o vetor D é igual ao vetor A menos o vetor B, mas a magnitude de D não é igual à magnitude de A menos o B. — Figura\(\PageIndex{3}\): A regra do paralelogramo para a adição de dois vetores. Faça a translação paralela de cada vetor até um ponto em que suas origens (marcadas pelo ponto) coincidam e construa um paralelogramo com dois lados nos vetores e os outros dois lados (indicados por linhas tracejadas) paralelos aos vetores. (a) Desenhe o vetor resultante\(\vec{R}\) ao longo da diagonal do paralelogramo do ponto comum ao canto oposto. O comprimento R do vetor resultante não é igual à soma das magnitudes dos dois vetores. (b) Desenhe o vetor de diferença\(\vec{D}\) =\(\vec{A}\) −\(\vec{B}\) ao longo da diagonal conectando as extremidades dos vetores. Coloque a origem do vetor\(\vec{D}\) no final do vetor\(\vec{B}\) e o final (ponta da seta) do vetor\(\vec{D}\) no final do vetor\(\vec{A}\). O comprimento D do vetor de diferença não é igual à diferença de magnitudes dos dois vetores.

Resulta da regra do paralelogramo que nem a magnitude do vetor resultante nem a magnitude do vetor de diferença podem ser expressas como uma simples soma ou diferença das magnitudes A e B, porque o comprimento de uma diagonal não pode ser expresso como uma simples soma dos comprimentos dos lados. Ao usar uma construção geométrica para encontrar magnitudes |\(\vec{R}\) | e |\(\vec{D}\) |, temos que usar leis de trigonometria para triângulos, o que pode levar a uma álgebra complicada. Há duas maneiras de contornar essa complexidade algébrica. Uma maneira é usar o método dos componentes, que examinaremos na próxima seção. A outra forma é desenhar os vetores em escala, como é feito na navegação, e ler comprimentos e ângulos vetoriais aproximados (direções) dos gráficos. Nesta seção, examinamos a segunda abordagem.

Se precisarmos adicionar três ou mais vetores, repetimos a regra do paralelogramo para os pares de vetores até encontrarmos a resultante de todas as resultantes. Para três vetores, por exemplo, primeiro encontramos a resultante do vetor 1 e do vetor 2 e, em seguida, encontramos a resultante dessa resultante e do vetor 3. A ordem na qual selecionamos os pares de vetores não importa porque a operação de adição vetorial é comutativa e associativa (veja Equação 2.2.7 e Equação 2.2.8). Antes de definirmos uma regra geral resultante de aplicações repetitivas da regra do paralelogramo, vejamos o exemplo a seguir.

Suponha que você planeje uma viagem de férias na Flórida. Saindo de Tallahassee, a capital do estado, você planeja visitar seu tio Joe em Jacksonville, ver seu primo Vinny em Daytona Beach, parar para se divertir em Orlando, assistir a uma apresentação de circo em Tampa e visitar a Universidade da Flórida em Gainesville. Sua rota pode ser representada por cinco vetores de deslocamento\(\vec{A}\)\(\vec{B}\)\(\vec{C}\),\(\vec{D}\),\(\vec{E}\), e, que são indicados pelos vetores vermelhos na Figura\(\PageIndex{4}\). Qual é o seu deslocamento total quando você chega a Gainesville? O deslocamento total é a soma vetorial de todos os cinco vetores de deslocamento, que pode ser encontrado usando a regra do paralelogramo quatro vezes. Como alternativa, lembre-se de que o vetor de deslocamento tem seu início na posição inicial (Tallahassee) e seu final na posição final (Gainesville), então o vetor de deslocamento total pode ser desenhado diretamente como uma seta conectando Tallahassee a Gainesville (veja o vetor verde na Figura\(\PageIndex{4}\)). Quando usamos a regra do paralelogramo quatro vezes, a resultante\(\vec{R}\) que obtemos é exatamente esse vetor verde conectando Tallahassee com Gainesville:\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) +\(\vec{C}\) +\(\vec{D}\) +\(\vec{E}\).

Um mapa da Flórida com os seguintes vetores mostrados em vermelho: Vetor A de Tallahassee a Jacksonville, quase a oeste. Vetor B de Jacksonville a Daytona Beach, sudeste. Vetor C de Daytona Beach a Orlando, sudoeste. Vetor D de Orlando a Tampa, sudoeste (mas menos vertical que o vetor C). Vetor E de Tampa a Gainesville, um pouco a leste do norte. O vetor R de Tallahassee a Gainsville é mostrado como uma seta verde. — Figura\(\PageIndex{4}\): Quando usamos a regra do paralelogramo quatro vezes, obtemos o vetor resultante\(\vec{R}\) =\(\vec{A}\) + + +\(\vec{B}\)\(\vec{C}\)\(\vec{D}\) +\(\vec{E}\), que é o vetor verde conectando Tallahassee com Gainesville.

O desenho do vetor resultante de muitos vetores pode ser generalizado usando a seguinte construção geométrica da cauda a cabeça. Suponha que desejemos desenhar o vetor resultante\(\vec{R}\) de quatro vetores\(\vec{A}\),\(\vec{B}\),\(\vec{C}\), e\(\vec{D}\) (Figura\(\PageIndex{5a}\)). Selecionamos qualquer um dos vetores como o primeiro vetor e fazemos uma tradução paralela de um segundo vetor para uma posição em que a origem (“cauda”) do segundo vetor coincide com a extremidade (“cabeça”) do primeiro vetor. Em seguida, selecionamos um terceiro vetor e fazemos uma tradução paralela do terceiro vetor para uma posição em que a origem do terceiro vetor coincide com o final do segundo vetor. Repetimos esse procedimento até que todos os vetores estejam em um arranjo da cabeça à cauda, como o mostrado na Figura\(\PageIndex{5}\). Desenhamos o vetor resultante\(\vec{R}\) conectando a origem (“cauda”) do primeiro vetor com a extremidade (“cabeça”) do último vetor. O final do vetor resultante está no final do último vetor. Como a adição de vetores é associativa e comutativa, obtemos o mesmo vetor resultante, independentemente de qual vetor escolhermos ser o primeiro, segundo, terceiro ou quarto nesta construção.

Na figura a, quatro vetores, rotulados A, B, C e D, são mostrados individualmente. Na figura b, os vetores são mostrados dispostos da cabeça à cauda: a cauda do vetor A está na cabeça de D. A cauda do vetor C está na cabeça de A. E a cauda do vetor B está na cabeça de C. Cada vetor está apontando na mesma direção da figura a. Um quinto vetor, R, começa na cauda do vetor D e termina na cabeça de vetor B. — Figura\(\PageIndex{5}\): Método cauda a cabeça para desenhar o vetor resultante\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) +\(\vec{C}\) +\(\vec{D}\). (a) Quatro vetores de diferentes magnitudes e direções. (b) Os vetores em (a) são traduzidos para novas posições em que a origem (“cauda”) de um vetor está no final (“cabeça”) de outro vetor. O vetor resultante é desenhado da origem (“cauda”) do primeiro vetor até a extremidade (“cabeça”) do último vetor nesse arranjo.

Exemplo\(\PageIndex{2}\): Geometric Construction of the Resultant

Os três vetores de deslocamento\(\vec{A}\)\(\vec{B}\), e\(\vec{C}\) na Figura\(\PageIndex{6}\) são especificados por suas magnitudes A = 10,0, B = 7,0 e C = 8,0, respectivamente, e por seus respectivos ângulos de direção com a direção horizontal\(\alpha\) = 35°,\(\beta\) = −110° e\(\gamma\) = 30°. As unidades físicas das magnitudes são centímetros. Escolha uma escala conveniente e use uma régua e um transferidor para encontrar as seguintes somas vetoriais: (a)\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\), (b)\(\vec{D}\) =\(\vec{A}\) −\(\vec{B}\) e (c)\(\vec{S}\) =\(\vec{A}\) −\(3 \vec{B}\) +\(\vec{C}\).

O vetor A tem magnitude 10,0 e está em um ângulo alfa = 35 graus no sentido anti-horário em relação à horizontal. Ele aponta para cima e para a direita. O vetor B tem magnitude 7,0 e está em um ângulo beta = -110 graus no sentido horário em relação à horizontal. Ele aponta para baixo e para a esquerda. O vetor C tem magnitude 8,0 e está em um ângulo gama = 30 graus no sentido anti-horário em relação à horizontal. Ele aponta para cima e para a direita. O vetor F tem magnitude 20,0 e está em um ângulo phi = 110 graus no sentido anti-horário em relação à horizontal. Ele aponta para cima e para a esquerda. — Figura\(\PageIndex{6}\): Vetores usados no Exemplo\(\PageIndex{2}\) e no recurso Exercício a seguir.

Estratégia

Na construção geométrica, encontrar um vetor significa encontrar sua magnitude e seu ângulo de direção com a direção horizontal. A estratégia é desenhar para dimensionar os vetores que aparecem no lado direito da equação e construir o vetor resultante. Em seguida, use uma régua e um transferidor para ler a magnitude da resultante e o ângulo de direção. Para as partes (a) e (b), usamos a regra do paralelogramo. Para (c) usamos o método cauda a cabeça.

Solução

Para as partes (a) e (b), associamos a origem do vetor\(\vec{B}\) à origem do vetor\(\vec{A}\), conforme mostrado na Figura\(\PageIndex{7}\), e construímos um paralelogramo. A diagonal mais curta desse paralelogramo é a soma\(\vec{A}\) +\(\vec{B}\). A maior das diagonais é a diferença\(\vec{A}\) -\(\vec{B}\). Usamos uma régua para medir os comprimentos das diagonais e um transferidor para medir os ângulos com a horizontal. Para o resultante\(\vec{R}\), obtemos R = 5,8 cm e\(\theta_{R}\) ≈ 0°. Para a diferença\(\vec{D}\), obtemos D = 16,2 cm e\(\theta_{D}\) = 49,3°, que são mostrados na Figura\(\PageIndex{7}\).

Três diagramas dos vetores A e B. Os vetores A e B são mostrados colocados de ponta a ponta. O vetor A aponta para cima e para a direita e tem magnitude 10,0. O vetor B aponta para baixo e para a esquerda e tem magnitude 7,0. O ângulo entre os vetores A e B é 145 graus. No segundo diagrama, os vetores A e B são mostrados novamente junto com as linhas tracejadas que completam o paralelogramo. O vetor R, igual à soma dos vetores A e B, é mostrado como o vetor das caudas de A e B até o vértice oposto do paralelogramo. A magnitude de R é 5,8. No terceiro diagrama, os vetores A e B são mostrados novamente junto com as linhas tracejadas que completam o paralelogramo. O vetor D, igual à diferença dos vetores A e B, é mostrado como o vetor da cabeça de B até a cabeça de A. A magnitude de D é 16,2 e o ângulo entre D e a horizontal é 49,3 graus. O vetor R no segundo diagrama é muito menor do que o vetor D no terceiro diagrama. — Figura\(\PageIndex{7}\): Usando a regra do paralelogramo para resolver (a) (encontrando a resultante, vermelho) e (b) (encontrando a diferença, azul).

Para (c), podemos começar com o vetor −3\(\vec{B}\) e desenhar os vetores restantes de ponta a ponta, conforme mostrado na Figura\(\PageIndex{8}\). Além do vetor, a ordem em que desenhamos os vetores não é importante, mas desenhar os vetores em escala é muito importante. Em seguida, desenhamos o vetor\(\vec{S}\) da origem do primeiro vetor até o final do último vetor e colocamos a ponta da seta no final de\(\vec{S}\). Usamos uma régua para medir o comprimento de\(\vec{S}\) e descobrimos que sua magnitude é S = 36,9 cm. Usamos um transferidor e descobrimos que seu ângulo de direção é\(\theta_{S}\) = 52,9°. Essa solução é mostrada na Figura\(\PageIndex{8}\).

Três vetores são mostrados em azul e colocados da cabeça à cauda: o vetor menos 3 B aponta para cima e para a direita e tem magnitude 3 B = 21,0. O vetor A começa na cabeça de B, aponta para cima e para a direita e tem uma magnitude de A=10,0. O ângulo entre o vetor A e o vetor menos 3 B é 145 graus. O vetor C começa na cabeça de A e tem magnitude C=8,0. O vetor S é verde e vai da cauda de menos 3 B até a cabeça de C. O vetor S é igual ao vetor A menos 3 vetor B mais o vetor C, tem uma magnitude de S = 36,9 e faz um ângulo de 52,9 graus no sentido anti-horário com a horizontal. — Figura\(\PageIndex{8}\): Usando o método cauda a cabeça para resolver (c) (vetor de descoberta\(\vec{S}\), verde).

Exercício 2.3

Usando os três vetores de deslocamento\(\vec{A}\)\(\vec{B}\),, e\(\vec{F}\) na Figura\(\PageIndex{6}\), escolha uma escala conveniente e use uma régua e um transferidor para encontrar o vetor\(\vec{G}\) dado pela equação vetorial\(\vec{G}\) =\(\vec{A}\) +\(2 \vec{B}\) −\(\vec{F}\).

Simulação

Observe a adição de vetores em um plano visitando esta calculadora vetorial e esta simulação PhET.