Skip to main content
Global

6.3: Explicando a Lei de Gauss

  1. Last updated
  2. Save as PDF
  • Page ID
    184579

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Lei estadual de Gauss
    • Explique as condições sob as quais a lei de Gauss pode ser usada
    • Aplique a lei de Gauss em sistemas apropriados

    Agora podemos determinar o fluxo elétrico através de uma superfície fechada arbitrária devido a uma distribuição arbitrária de carga. Descobrimos que, se uma superfície fechada não tiver nenhuma carga dentro de onde uma linha de campo elétrico possa terminar, qualquer linha de campo elétrico que entre na superfície em um ponto deve necessariamente sair em algum outro ponto da superfície. Portanto, se uma superfície fechada não tiver nenhuma carga dentro do volume fechado, o fluxo elétrico através da superfície será zero. Agora, o que acontece com o fluxo elétrico se houver algumas cargas dentro do volume fechado? A lei de Gauss dá uma resposta quantitativa a essa questão.

    Para ter uma ideia do que esperar, vamos calcular o fluxo elétrico através de uma superfície esférica em torno de uma carga pontual positiva\(q\), já que já conhecemos o campo elétrico em tal situação. Lembre-se de que quando colocamos a carga pontual na origem de um sistema de coordenadas, o campo elétrico em um ponto\(P\) que está distante\(r\) da carga na origem é dado por

    \[\vec{E}_p = \dfrac{1}{4\pi \epsilon_0}\dfrac{q}{r^2}\hat{r},\]

    onde\(\hat{r}\) está o vetor radial da carga na origem até o ponto P. Podemos usar esse campo elétrico para encontrar o fluxo através da superfície esférica do raio r, conforme mostrado na Figura\(\PageIndex{1}\).

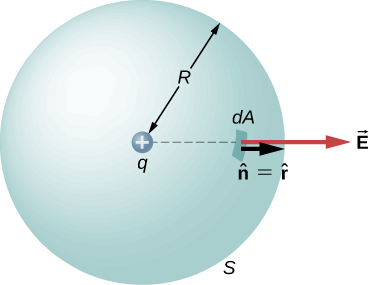
    Uma esfera chamada S com raio R é mostrada. No centro, há um pequeno círculo com um sinal de mais, rotulado q. Uma pequena mancha na esfera é chamada dA. Duas setas apontam para fora daqui, perpendiculares à superfície da esfera. A seta menor é rotulada em 1 igual a ou chapéu. A seta mais longa é rotulada como vetor E.
    Figura\(\PageIndex{1}\): Uma superfície esférica fechada ao redor de uma carga pontual q.

    Em seguida, aplicamos\(\Phi = \int_S \vec{E} \cdot \hat{n} dA\) a esse sistema e substituímos os valores conhecidos. Na esfera,\(\hat{n}\) e\(r = R\) assim para uma área infinitesimal dA,

    \[\begin{align*} d\Phi &= \vec{E} \cdot \hat{n} dA \\[4pt] &= \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} \hat{r} \cdot \hat{r} dA \\[4pt] &= \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} dA. \end{align*}\]

    Agora, encontramos o fluxo líquido integrando esse fluxo sobre a superfície da esfera:

    \[\Phi = \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} \oint_S dA = \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} (4\pi R^2) = \dfrac{q}{\epsilon_0}.\]

    onde está a área total da superfície esférica\(4\pi R^2\). Isso fornece o fluxo através da superfície esférica fechada em um raio\(r\) como

    \[\Phi = \dfrac{q}{\epsilon_0}.\]

    Um fato notável sobre essa equação é que o fluxo é independente do tamanho da superfície esférica. Isso pode ser atribuído diretamente ao fato de que o campo elétrico de uma carga pontual diminui conforme\(1/r^2\) a distância, o que apenas cancela a\(r^2\) taxa de aumento da área superficial.

    Imagem de linhas de campo elétrico

    Uma forma alternativa de ver por que o fluxo através de uma superfície esférica fechada é independente do raio da superfície é observar as linhas do campo elétrico. Observe que cada linha de campo de q que perfura a superfície no raio\(R_1\) também perfura a superfície em\(R_2\) (Figura\(\PageIndex{2}\)).

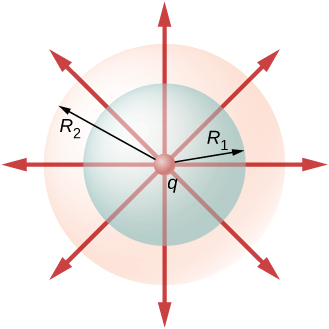
    A figura mostra três círculos concêntricos. O menor no centro é rotulado como q, o do meio tem raio R1 e o maior tem raio R2. Oito flechas irradiam para fora do centro em todas as oito direções.
    Figura\(\PageIndex{2}\): O fluxo através de superfícies esféricas de raios\(R_1\) e o\(R_2\) fechamento de uma carga q são iguais, independentemente do tamanho da superfície, uma vez que todas as linhas do campo E que perfuram uma superfície da direção interna para externa também perfuram a outra superfície no mesma direção.

    Portanto, o número líquido de linhas de campo elétrico que passam pelas duas superfícies da direção interna para externa é igual. Esse número líquido de linhas de campo elétrico, obtido subtraindo o número de linhas na direção de fora para dentro do número de linhas na direção de dentro para fora, fornece uma medida visual do fluxo elétrico através das superfícies.

    Você pode ver que, se nenhuma carga estiver incluída em uma superfície fechada, o fluxo elétrico através dela deverá ser zero. Uma linha de campo típica entra na superfície\(dA_1\) e sai em\(dA_2\). Cada linha que entra na superfície também deve sair dessa superfície. Portanto, o “fluxo” líquido das linhas de campo para dentro ou para fora da superfície é zero (Figura\(\PageIndex{3a}\)). O mesmo acontece se cargas de sinal igual e oposto forem incluídas dentro da superfície fechada, de forma que a carga total incluída seja zero (Figura\(\PageIndex{3b}\)). Uma superfície que inclui a mesma quantidade de carga tem o mesmo número de linhas de campo que a cruzam, independentemente da forma ou tamanho da superfície, desde que a superfície inclua a mesma quantidade de carga (Figura\(\PageIndex{3c}\)).

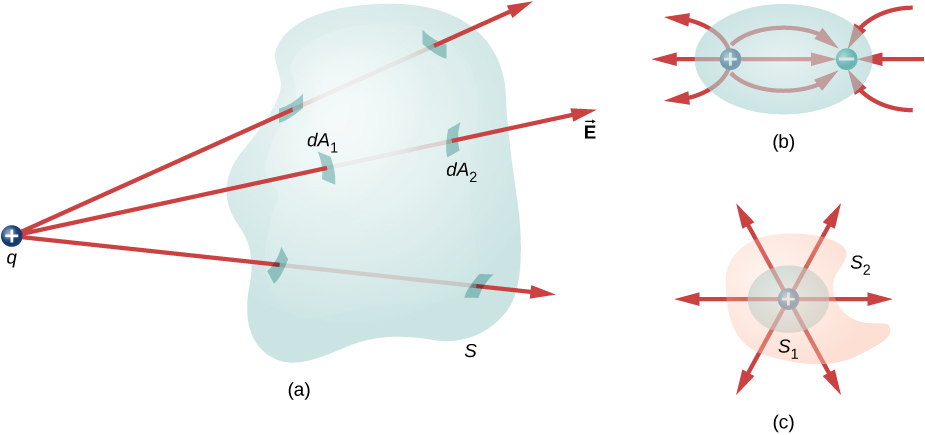
    A Figura a mostra uma forma tridimensional irregular chamada S. Um pequeno círculo com um sinal de mais, rotulado q, está fora dele. Três setas rotuladas como vetor E se originam de q e passam por S. As manchas onde as setas perfuram a superfície de S são destacadas. A mancha em que uma seta entra na forma é rotulada como dA1 e a mancha em que a seta emerge da forma é rotulada como dA2. A Figura b mostra um oval com dois pequenos círculos dentro dele. Eles são rotulados como mais e menos. Três flechas de fora do ponto oval até o círculo rotulado com menos. Três setas apontam de mais para menos. Três setas apontam de mais para fora do oval. A Figura c tem uma forma irregular chamada S2. Dentro dele está um círculo chamado S1. No centro, há um pequeno círculo rotulado como plus. Seis flechas irradiam daqui em direções diferentes.
    Figura\(\PageIndex{3}\): Entendendo o fluxo em termos de linhas de campo. (a) O fluxo elétrico através de uma superfície fechada devido a uma carga fora dessa superfície é zero. (b) As cargas são fechadas, mas como a carga líquida incluída é zero, o fluxo líquido através da superfície fechada também é zero. (c) A forma e o tamanho das superfícies que envolvem uma carga não importam porque todas as superfícies que envolvem a mesma carga têm o mesmo fluxo.

    Declaração da Lei de Gauss

    A lei de Gauss generaliza esse resultado para o caso de qualquer número de cargas e qualquer localização das cargas no espaço dentro da superfície fechada. De acordo com a lei de Gauss, o fluxo do campo elétrico\(\vec{E}\) através de qualquer superfície fechada, também chamada de superfície gaussiana, é igual à carga líquida fechada\((q_{enc})\) dividida pela permissividade do espaço livre\((\epsilon_0)\):

    \[\Phi_{Closed \, Surface} = \dfrac{q_{enc}}{\epsilon_0}.\]

    Essa equação vale para cargas de qualquer um dos signos, porque definimos o vetor de área de uma superfície fechada para apontar para fora. Se a carga incluída for negativa (Figura\(\PageIndex{4b}\)), o fluxo através de um\(S\) ou\(S'\) será negativo.

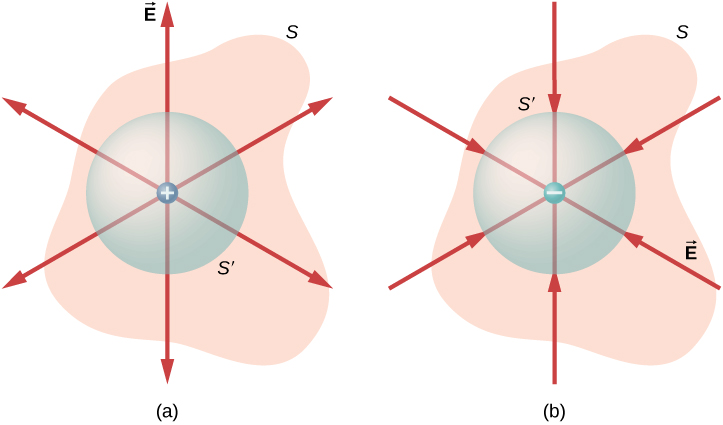
    A figura a tem uma forma irregular chamada S. Dentro dela está um círculo chamado S prime. No centro, há um pequeno círculo rotulado como plus. Seis flechas irradiam daqui em direções diferentes. A figura b tem a mesma forma irregular S e o círculo S primo. No centro, há um pequeno círculo rotulado com menos. Seis flechas de diferentes direções irradiam para dentro até menos.
    Figura\(\PageIndex{4}\): O fluxo elétrico através de qualquer superfície fechada ao redor de uma carga pontual q é dado pela lei de Gauss. (a) A carga fechada é positiva. (b) A carga fechada é negativa.

    A superfície gaussiana não precisa corresponder a um objeto físico real; na verdade, raramente corresponderá. É uma construção matemática que pode ter qualquer formato, desde que esteja fechada. No entanto, como nosso objetivo é integrar o fluxo sobre ele, tendemos a escolher formas altamente simétricas.

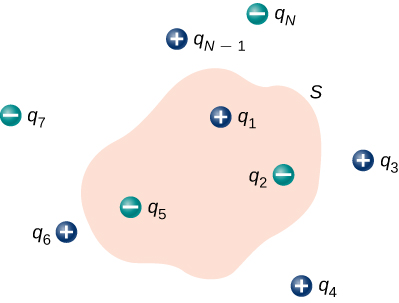
    Se as cobranças forem de pontos discretos, basta adicioná-las. Se a carga for descrita por uma distribuição contínua, precisamos nos integrar adequadamente para encontrar a carga total que reside dentro do volume fechado. Por exemplo, o fluxo através da superfície gaussiana\(S\) da Figura\(\PageIndex{5}\) é

    \[\Phi = (q_1 + q_2 + q_5)/\epsilon_0.\]

    Observe que\(q_{enc}\) é simplesmente a soma das cobranças de pontos. Se a distribuição de carga fosse contínua, precisaríamos nos integrar adequadamente para calcular a carga total dentro da superfície gaussiana.

    A figura mostra uma forma irregular chamada S. Dentro dela estão as cargas rotuladas como positivas q1 e negativas q2 e q5. Fora de S estão as cargas rotuladas como positivas q3, q4, q6 e q N menos 1 e negativas q7 e q N.
    Figura\(\PageIndex{5}\): O fluxo através da superfície gaussiana mostrado, devido à distribuição de carga, é\(\Phi = (q_1 + q_2 + q_5)/\epsilon_0\).

    Lembre-se de que o princípio da superposição vale para o campo elétrico. Portanto, o campo elétrico total em qualquer ponto, incluindo aqueles na superfície gaussiana escolhida, é a soma de todos os campos elétricos presentes nesse ponto. Isso nos permite escrever a lei de Gauss em termos do campo elétrico total.

    Lei de Gauss

    O fluxo\(\Phi\) do campo elétrico\(\vec{E}\) através de qualquer superfície fechada S (uma superfície gaussiana) é igual à carga líquida fechada\((q_{enc})\) dividida pela permissividade do espaço livre\((\epsilon_0)\):

    \[\Phi = \oint_S \vec{E} \cdot \hat{n} dA = \dfrac{q_{enc}}{\epsilon_0}.\]

    Para usar a lei de Gauss de forma eficaz, você deve ter uma compreensão clara do que cada termo na equação representa. O campo\(\vec{E}\) é o campo elétrico total em cada ponto da superfície gaussiana. Esse campo total inclui contribuições de cargas dentro e fora da superfície gaussiana. No entanto,\(q_{enc}\) é apenas a carga dentro da superfície gaussiana. Finalmente, a superfície gaussiana é qualquer superfície fechada no espaço. Essa superfície pode coincidir com a superfície real de um condutor ou pode ser uma superfície geométrica imaginária. O único requisito imposto a uma superfície gaussiana é que ela seja fechada (Figura\(\PageIndex{5}\)).

    A figura mostra uma garrafa que parece um frasco invertido cujo gargalo é alongado, dobrado para cima, torcido, levado para dentro da garrafa e unido à sua base, tendo assim apenas uma superfície.
    Figura\(\PageIndex{6}\): Uma garrafa de Klein parcialmente cheia com um líquido. A garrafa Klein poderia ser usada como uma superfície gaussiana?
    Exemplo\(\PageIndex{1}\): Electric Flux through Gaussian Surfaces

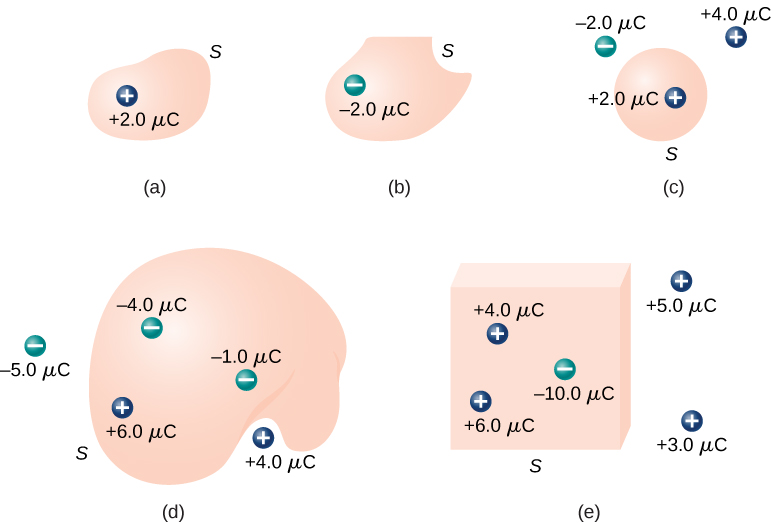
    Calcule o fluxo elétrico através de cada superfície gaussiana mostrada na Figura\(\PageIndex{7}\).

    As figuras de a a d mostram formas irregulares e a figura e mostra um cubo. A Figura a tem uma carga dentro da forma rotulada mais 2,0 mu C. A Figura b tem uma carga dentro da forma rotulada menos 2,0 mu C. A Figura c tem uma carga dentro da forma rotulada mais 2,0 mu C e duas cargas externas rotuladas mais 4 mu C e menos 2,0 mu C. A Figura d tem três cargas dentro da forma rotuladas menos 1,0 mu C, menos 4,0 mu C e mais 6,0 mu C e duas cargas fora da forma rotulada menos 5,0 mu C e mais 4,0 mu C. A Figura e tem três cargas internas rotuladas mais 4,0 mu C, mais 6,0 mu C e menos 10,0 mu C e duas cargas fora do cubo rotuladas mais 5,0 mu C e 3,0 mu C.
    Figura\(\PageIndex{7}\): Várias superfícies e cargas gaussianas.

    Estratégia

    Pela lei de Gauss, o fluxo através de cada superfície é dado por\(q_{enc}/\epsilon_0\), onde\(q_{enc}\) está a carga encerrada por essa superfície.

    Solução

    Para as superfícies e cargas mostradas, encontramos

    uma\(\Phi = \frac{2.0 \, \mu C}{\epsilon_0} = 2.3 \times 10^5 N \cdot m^2/C\).

    \(\Phi = \frac{-2.0 \, \mu C}{\epsilon_0} = -2.3 \times 10^5 N \cdot m^2/C\)b.

    \(\Phi = \frac{2.0 \, \mu C}{\epsilon_0} = 2.3 \times 10^5 N \cdot m^2/C\)c.

    \(\frac{-4.0 \, \mu C + 6.0 \, \mu C - 1.0 \, \mu C}{\epsilon_0} = 1.1 \times 10^5 N \cdot m^2/C\)d.

    \(\frac{4.0 \, \mu C + 6.0 \, \mu C - 10.0 \, \mu C}{\epsilon_0} = 0\)e.

    Significância

    No caso especial de uma superfície fechada, os cálculos de fluxo se tornam uma soma de cargas. Na próxima seção, isso nos permitirá trabalhar com sistemas mais complexos.

    Exercício\(\PageIndex{1}\)

    Calcule o fluxo elétrico através da superfície cúbica fechada para cada distribuição de carga mostrada na Figura\(\PageIndex{8}\).

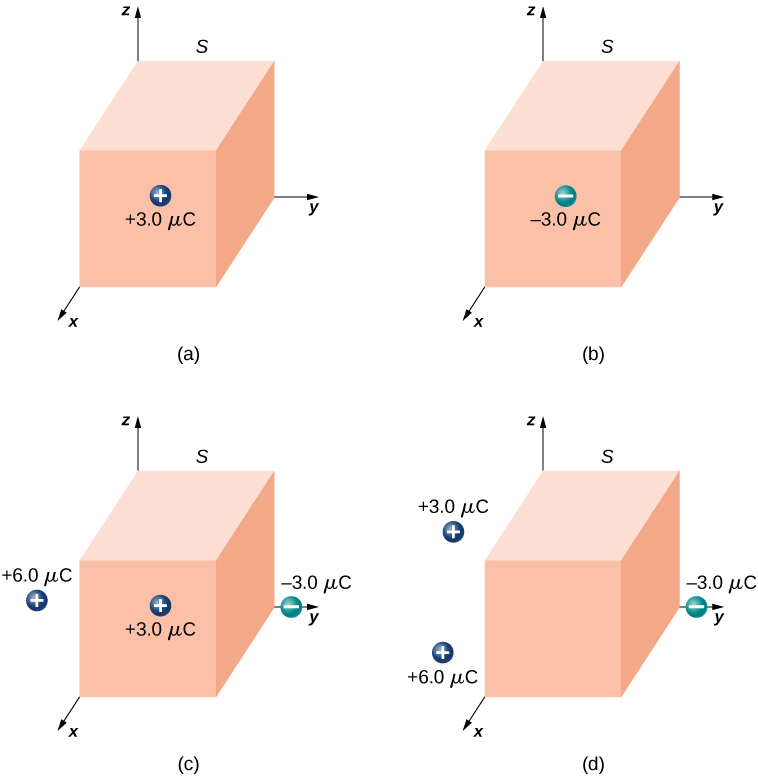
    As figuras de a a d mostram um cubóide com um canto na origem dos eixos coordenados. Na figura a, há uma carga mais 3,0 mu C na superfície paralela ao plano yz. Na figura b, há uma carga menos 3,0 mu C na superfície paralela ao plano yz. Na figura c, há uma carga mais 3,0 mu C na superfície paralela ao plano yz, uma carga menos 3,0 mu C no eixo y fora da forma e uma carga mais 6,0 mu C fora da forma. Na figura d, há uma carga menos 3,0 mu C no eixo y fora da forma e cargas mais 3,0 mu C e mais 6,0 mu C fora da forma.
    Figura\(\PageIndex{8}\): Uma superfície cúbica gaussiana com várias distribuições de carga.
    Responda a

    \(3.4 \times 10^5 N \cdot m^2/C\)

    Resposta b

    \(-3.4 \times 10^5 N \cdot m^2/C\)

    Resposta c

    \(3.4 \times 10^5 N \cdot m^2/C\)

    Resposta d

    0

    Use essa simulação para ajustar a magnitude da carga e o raio da superfície gaussiana ao redor dela. Veja como isso afeta o fluxo total e a magnitude do campo elétrico na superfície gaussiana.