6.4: Aplicando a Lei de Gauss

Objetivos de

Ao final desta seção, você poderá:

• Explique o que é simetria esférica, cilíndrica e plana
• Reconheça se um determinado sistema possui ou não uma dessas simetrias
• Aplique a lei de Gauss para determinar o campo elétrico de um sistema com uma dessas simetrias

A lei de Gauss é muito útil para determinar expressões para o campo elétrico, mesmo que a lei não seja diretamente sobre o campo elétrico; é sobre o fluxo elétrico. Acontece que em situações que têm certas simetrias (esféricas, cilíndricas ou planares) na distribuição de carga, podemos deduzir o campo elétrico com base no conhecimento do fluxo elétrico. Nesses sistemas, podemos encontrar uma superfície gaussiana S sobre a qual o campo elétrico tem magnitude constante. Além disso,\(\vec{E}\) é paralelo a\(\hat{n}\) todos os lugares na superfície, então\(\vec{E} \cdot \hat{n} = E\). (Se\(\vec{E}\) e\(\hat{n}\) forem antiparalelos em todos os lugares da superfície,\(\vec{E} \cdot \hat{n} = - E\).) A lei de Gauss então simplifica para

\[\Phi = \oint_S \vec{E} \cdot \hat{n} dA = E \oint_S dA = EA = \dfrac{q_{enc}}{\epsilon_0},\]

onde A é a área da superfície. Observe que essas simetrias levam à transformação da integral de fluxo em um produto da magnitude do campo elétrico e de uma área apropriada. Quando você usa esse fluxo na expressão da lei de Gauss, você obtém uma equação algébrica que pode ser resolvida para a magnitude do campo elétrico, que se parece com

\[E \approx \dfrac{q_{enc}}{\epsilon_0 \, area}.\]

A direção do campo elétrico no ponto P é obtida a partir da simetria da distribuição de carga e do tipo de carga na distribuição. Portanto, a lei de Gauss pode ser usada para determinar\(\vec{E}\). Aqui está um resumo das etapas que seguiremos:

Estratégia de resolução de problemas: Lei de Gauss

1. Identifique a simetria espacial da distribuição de carga. Este é um primeiro passo importante que nos permite escolher a superfície gaussiana apropriada. Como exemplos, uma carga pontual isolada tem simetria esférica e uma linha infinita de carga tem simetria cilíndrica.
2. Escolha uma superfície gaussiana com a mesma simetria da distribuição de carga e identifique suas consequências. Com esta escolha,\(\vec{E} \cdot \hat{n}\) é facilmente determinado sobre a superfície gaussiana.
3. Avalie a integral\(\oint_S \vec{E} \cdot \hat{n} dA\) sobre a superfície gaussiana, ou seja, calcule o fluxo através da superfície. A simetria da superfície gaussiana nos permite fatorar\(\vec{E} \cdot \hat{n}\) fora da integral.
4. Determine a quantidade de carga envolvida pela superfície gaussiana. Esta é uma avaliação do lado direito da equação que representa a lei de Gauss. Muitas vezes, é necessário realizar uma integração para obter a carga líquida fechada.
5. Avalie o campo elétrico da distribuição de carga. Agora, o campo pode ser encontrado usando os resultados das etapas 3 e 4.

Basicamente, existem apenas três tipos de simetria que permitem que a lei de Gauss seja usada para deduzir o campo elétrico. Eles são

• Uma distribuição de carga com simetria esférica
• Uma distribuição de carga com simetria cilíndrica
• Uma distribuição de carga com simetria planar

Para explorar a simetria, realizamos os cálculos em sistemas de coordenadas apropriados e usamos o tipo certo de superfície gaussiana para essa simetria, aplicando as quatro etapas restantes.

Distribuição de carga com simetria esférica

Uma distribuição de carga tem simetria esférica se a densidade da carga depender apenas da distância de um ponto no espaço e não da direção. Em outras palavras, se você girar o sistema, ele não parecerá diferente. Por exemplo, se uma esfera de raio R é uniformemente carregada com densidade de carga\(\rho_0\), a distribuição tem simetria esférica (Figura\(\PageIndex{1a}\)). Por outro lado, se uma esfera de raio R for carregada de forma que a metade superior da esfera tenha densidade de carga uniforme\(\rho_1\) e a metade inferior tenha uma densidade de carga uniforme\(\rho_2 \neq \rho_1\), a esfera não tem simetria esférica porque a densidade de carga depende da direção (Figura \(\PageIndex{1b}\)). Portanto, não é a forma do objeto, mas sim a forma da distribuição de carga que determina se um sistema tem ou não simetria esférica.

A figura\(\PageIndex{1c}\) mostra uma esfera com quatro camadas diferentes, cada uma com sua própria densidade de carga uniforme. Embora seja uma situação em que a densidade de carga na esfera inteira não seja uniforme, a função de densidade de carga depende apenas da distância do centro e não da direção. Portanto, essa distribuição de carga tem simetria esférica.

Figura\(\PageIndex{1}\): Ilustrações de sistemas esféricos simétricos e não simétricos. Diferentes tonalidades indicam diferentes densidades de carga. Cargas em objetos de formato esférico não significam necessariamente que as cargas sejam distribuídas com simetria esférica. A simetria esférica ocorre somente quando a densidade da carga não depende da direção. Em (a), as cargas são distribuídas uniformemente em uma esfera. Em (b), a metade superior da esfera tem uma densidade de carga diferente da metade inferior; portanto, (b) não tem simetria esférica. Em (c), as cargas estão em camadas esféricas de diferentes densidades de carga, o que significa que a densidade de carga é apenas uma função da distância radial do centro; portanto, o sistema tem simetria esférica.

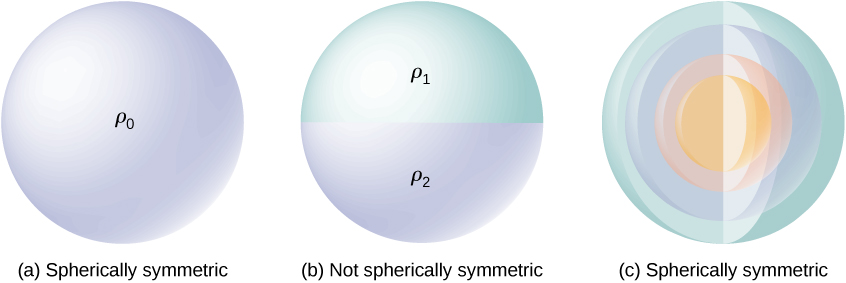
Uma boa maneira de determinar se seu problema tem ou não simetria esférica é observar a função de densidade de carga em coordenadas esféricas,\(\rho(r, \theta, \phi)\). Se a densidade de carga for apenas uma função de r, ou seja\(\rho = \rho(r)\), você terá simetria esférica. Se a densidade depender de\(\theta\) ou\(\phi\), você poderia alterá-la por rotação; portanto, você não teria simetria esférica.

Consequências da simetria

Em todos os casos esfericamente simétricos, o campo elétrico em qualquer ponto deve ser direcionado radialmente, porque a carga e, portanto, o campo devem ser invariantes sob rotação. Portanto, usando coordenadas esféricas com suas origens no centro da distribuição esférica de carga, podemos anotar a forma esperada do campo elétrico em um ponto P localizado a uma distância r do centro:

\[Spherical \, symmetry: \, \vec{E}_p = E_p(r)\hat{r},\]

onde\(\hat{r}\) é o vetor unitário apontado na direção da origem até o ponto de campo P. O componente radial\(E_p\) do campo elétrico pode ser positivo ou negativo. Quando\(E_p > 0\), o campo elétrico em P aponta para longe da origem e quando\(E_p < 0\), o campo elétrico em P aponta para a origem.

Cálculos gaussianos de superfície e fluxo

Agora podemos usar essa forma do campo elétrico para obter o fluxo do campo elétrico através da superfície gaussiana. Para simetria esférica, a superfície gaussiana é uma superfície esférica fechada que tem o mesmo centro do centro da distribuição de carga. Assim, a direção do vetor de área de um elemento de área na superfície gaussiana em qualquer ponto é paralela à direção do campo elétrico nesse ponto, pois ambos são direcionados radialmente para fora (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): O campo elétrico em qualquer ponto da superfície esférica gaussiana para uma distribuição de carga esfericamente simétrica é paralelo ao vetor do elemento de área nesse ponto, fornecendo fluxo como o produto da magnitude do campo elétrico e o valor da área. Observe que o raio R da distribuição de carga e o raio r da superfície gaussiana são quantidades diferentes.

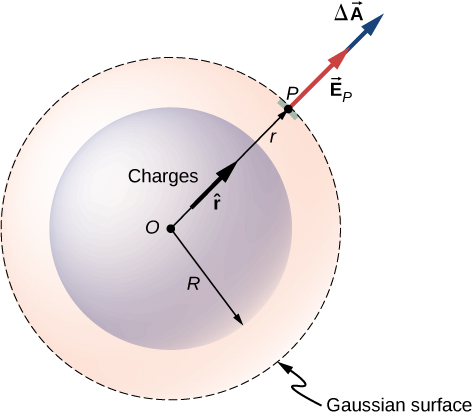
A magnitude do campo elétrico\(\vec{E}\) deve ser a mesma em todos os lugares em uma superfície esférica gaussiana concêntrica à distribuição. Para uma superfície esférica de raio r:

\[\Phi = \oint_S \vec{E}_p \cdot \hat{n} dA = E_p \oint_S dA = E_p \, 4\pi r^2.\]

Usando a lei de Gauss

De acordo com a lei de Gauss, o fluxo através de uma superfície fechada é igual à carga total dentro da superfície fechada dividida pela permissividade do vácuo\(\epsilon_0\). \(q_{enc}\)Seja a carga total dentro da distância r da origem, que é o espaço dentro da superfície esférica gaussiana do raio r. Isso dá a seguinte relação com a lei de Gauss:

\[4\pi r^2 E = \dfrac{q_{enc}}{\epsilon_0}.\]

Portanto, o campo elétrico no ponto P, que está a uma distância r do centro de uma distribuição de carga esfericamente simétrica, tem a seguinte magnitude e direção:

\[Magnitude: \, E(r) = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{enc}}{r^2}\]

Direção: radial de O a P ou de P a O.

A direção do campo no ponto P depende se a carga na esfera é positiva ou negativa. Para uma carga positiva líquida dentro da superfície gaussiana, a direção é de O a P, e para uma carga negativa líquida, a direção é de P a O. Isso é tudo o que precisamos para uma cobrança de pontos, e você notará que o resultado acima é idêntico ao de uma cobrança de pontos. No entanto, a lei de Gauss se torna verdadeiramente útil nos casos em que a carga ocupa um volume finito.

Computando a carga fechada

O caso mais interessante é quando uma distribuição esférica de carga ocupa um volume, e perguntar qual é o campo elétrico dentro da distribuição de carga se torna relevante. Nesse caso, a carga incluída depende da distância r do ponto de campo em relação ao raio da distribuição de carga R, como a mostrada na Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Uma distribuição de carga esfericamente simétrica e a superfície gaussiana usada para encontrar o campo (a) dentro e (b) fora da distribuição.

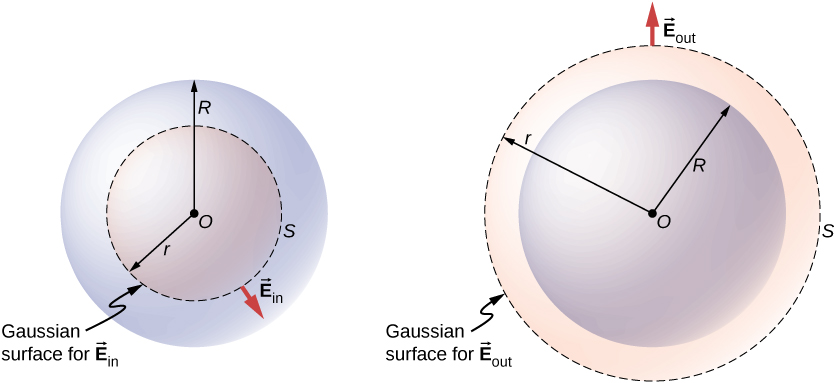
Se o ponto P estiver localizado fora da distribuição de carga, ou seja, se\(r \geq R\), a superfície gaussiana contendo P incluirá todas as cargas na esfera. Nesse caso,\(q_{enc}\) é igual à carga total na esfera. Por outro lado, se o ponto P estiver dentro da distribuição esférica de carga, ou seja, se\(r < R\), então a superfície gaussiana envolve uma esfera menor do que a esfera de distribuição de carga. Neste caso,\(q_{enc}\) é menor do que a carga total presente na esfera. Referindo-se à Figura\(\PageIndex{3}\), podemos escrever\(q_{enc}\) como

\[q_{enc} = q_{tot} (total \, charge) \, if \, r \geq R\]

\[q_{enc} = q_{within \, r < R} (only \, charge \, within \, r < R) \, if \, r < R\]

O campo em um ponto fora da distribuição de carga também é chamado\(\vec{E}_{out}\), e o campo em um ponto dentro da distribuição de carga é chamado\(\vec{E}_{in}\). Concentrando-se nos dois tipos de pontos de campo, dentro ou fora da distribuição de carga, agora podemos escrever a magnitude do campo elétrico como

\[P \, outside \, sphere \, E_{out} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{tot}}{r^2}\]

\[P \, inside \, sphere \, E_{in} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{within \, r < R}}{r^2}.\]

Observe que o campo elétrico fora de uma distribuição de carga esfericamente simétrica é idêntico ao de uma carga pontual no centro que tem uma carga igual à carga total da distribuição de carga esférica. Isso é notável, pois as cobranças não estão localizadas apenas no centro. Agora elaboramos exemplos específicos de distribuições esféricas de carga, começando com o caso de uma esfera uniformemente carregada.

Esfera uniformemente carregada

Uma esfera de raio R, como a mostrada na Figura\(\PageIndex{3}\), tem uma densidade de carga de volume uniforme\(\rho_0\). Encontre o campo elétrico em um ponto fora da esfera e em um ponto dentro da esfera.

Estratégia

Aplique a estratégia de resolução de problemas da lei de Gauss, onde já elaboramos o cálculo do fluxo.

Solução

A carga envolta pela superfície gaussiana é dada por

\[q_{enc} = \int \rho_0 dV = \int_0^r \rho_0 4\pi r'^2 dr' = \rho \left(\dfrac{4}{3} \pi r^3\right).\]

A resposta para a amplitude do campo elétrico pode então ser anotada imediatamente para um ponto fora da esfera, rotulado\(E_{out}\) e um ponto dentro da esfera, rotulado\(E_{in}\).

\[E_{out} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{tot}}{r^2}, \, q_{tot} = \dfrac{4}{3} \pi R^3 \, \rho_0,\]

\[E_{in} = \dfrac{q_{enc}}{4\pi \epsilon_0 r^2} = \dfrac{\rho_0r}{3 \epsilon_0}, \, since \, q_{enc} = \dfrac{4}{3} \pi r^3 \rho_0.\]

É interessante notar que a magnitude do campo elétrico aumenta dentro do material à medida que você sai, pois a quantidade de carga envolvida pela superfície gaussiana aumenta com o volume. Especificamente, a carga fechada cresce\(\propto r^3\), enquanto o campo de cada elemento infinitesimal de carga cai\(\propto 1/r^2\) com o resultado líquido de que o campo elétrico dentro da distribuição aumenta em intensidade linearmente com o raio. A magnitude do campo elétrico fora da esfera diminui à medida que você se afasta das cargas, porque a carga incluída permanece a mesma, mas a distância aumenta. A figura\(\PageIndex{4}\) mostra a variação da magnitude do campo elétrico com a distância do centro de uma esfera uniformemente carregada.

Figura\(\PageIndex{4}\): O campo elétrico de uma esfera não condutora uniformemente carregada aumenta dentro da esfera até um máximo na superfície e depois diminui como\(1/r^2\). Aqui,\(E_R = \frac{\rho_0 R}{3 \epsilon_0}\). O campo elétrico é devido a uma distribuição esférica de carga de densidade de carga uniforme e carga total Q em função da distância do centro da distribuição.

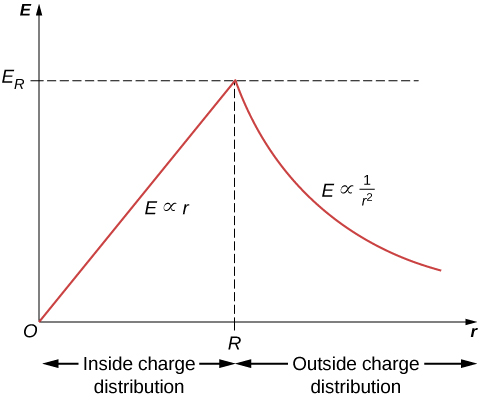
A direção do campo elétrico em qualquer ponto P é radialmente para fora da origem, se\(\rho_0\) for positiva, e para dentro (ou seja, em direção ao centro), se\(\rho_0\) for negativa. O campo elétrico em alguns pontos espaciais representativos é exibido na Figura\(\PageIndex{5}\) cujas coordenadas radiais r são\(r = R/2, \, r = R,\)\(r = 2R\) e.

Figura\(\PageIndex{5}\): Vetores de campo elétrico dentro e fora de uma esfera uniformemente carregada.

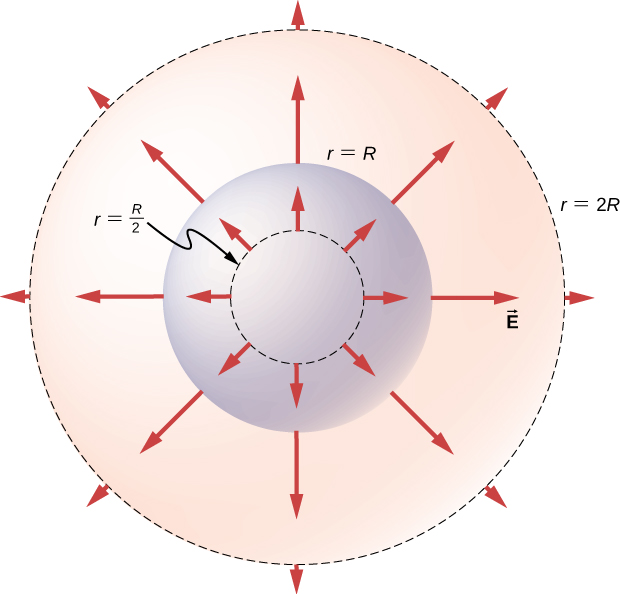
Significância

Observe que\(E_{out}\) tem a mesma forma da equação do campo elétrico de uma carga pontual isolada. Ao determinar o campo elétrico de uma distribuição esférica uniforme de carga, podemos, portanto, supor que toda a carga dentro da superfície gaussiana esférica apropriada está localizada no centro da distribuição.

Esfera não uniformemente carregada

Uma esfera não condutora de raio R tem uma densidade de carga não uniforme que varia com a distância de seu centro, conforme dada por

\[\rho(r) = ar^n (r \leq R; \, n \geq 0), \nonumber\]

onde a é uma constante. Exigimos\(n \geq 0\) que a densidade de carga não seja indefinida em\(r = 0\). Encontre o campo elétrico em um ponto fora da esfera e em um ponto dentro da esfera.

Estratégia

Aplique a estratégia da lei de Gauss dada acima, onde calculamos as integrais de carga fechadas separadamente para casos dentro e fora da esfera.

Solução

Como a função de densidade de carga dada tem apenas uma dependência radial e nenhuma dependência da direção, temos uma situação esfericamente simétrica. Portanto, a magnitude do campo elétrico em qualquer ponto é dada acima e a direção é radial. Só precisamos encontrar a carga incluída\(q_{enc}\), que depende da localização do ponto de campo.

Uma observação sobre símbolos: usamos\(r'\) para localizar cargas na distribuição de carga e r para localizar o (s) ponto (s) de campo na (s) superfície (s) gaussiana (s). A letra R é usada para o raio da distribuição de carga.

Como a densidade de carga não é constante aqui, precisamos integrar a função de densidade de carga sobre o volume fechado pela superfície gaussiana. Portanto, configuramos o problema para cargas em uma camada esférica, digamos entre\(r'\) e\(r' + dr'\) conforme mostrado na Figura\(\PageIndex{6}\). O volume de cargas na casca de largura infinitesimal é igual ao produto da área da superfície\(4\pi r'^2\) e da espessura\(dr'\). Multiplicar o volume pela densidade nesse local, ou seja\(ar'^n\), fornece a carga na casca:

\[dq = ar'^n 4\pi r'^2 dr'. \nonumber\]

Figura\(\PageIndex{6}\): Simetria esférica com distribuição de carga não uniforme. Nesse tipo de problema, precisamos de quatro raios: R é o raio da distribuição de carga, r é o raio da superfície gaussiana,\(r'\) é o raio interno da camada esférica e\(r' + dr'\) é o raio externo da concha esférica. A concha esférica é usada para calcular a carga dentro da superfície gaussiana. O intervalo para\(r'\) é de 0 a r para o campo em um ponto dentro da distribuição de carga e de 0 a R para o campo em um ponto fora da distribuição de carga. Se\(r > R\), então, a superfície gaussiana tem mais volume do que a distribuição de carga, mas o volume adicional não contribui\(q_{enc}\).

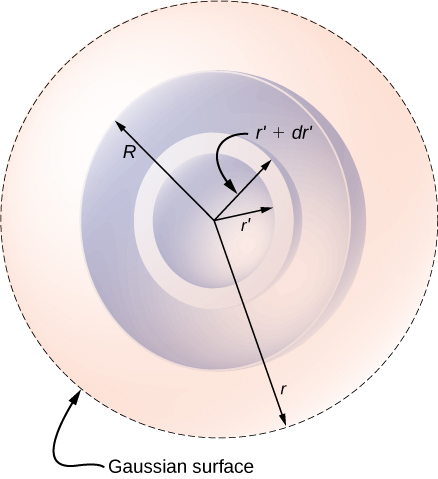
(a) Campo em um ponto fora da distribuição de cobrança. Nesse caso, a superfície gaussiana, que contém o ponto de campo P, tem um raio r maior que o raio R da distribuição de carga,\(r > R\). Portanto, todas as cargas da distribuição de carga estão dentro da superfície gaussiana. Observe que o espaço entre\(r' = R\) e\(r' = r\) está vazio de cargas e, portanto, não contribui para a integral sobre o volume delimitado pela superfície gaussiana:

\[q_{enc} = \int dq = \int_0^R ar'^n 4\pi r'^2 dr' = \dfrac{4\pi a}{n + 3} R^{n+3}. \nonumber\]

Isso é usado no resultado geral\(E_{out}\) acima para obter o campo elétrico em um ponto fora da distribuição de carga como

\[ \vec{E}_{out} = \left[ \dfrac{aR^{n+3}}{\epsilon_0(n + 3)} \right] \dfrac{1}{r^2} \hat{r}, \nonumber\]

onde\(\hat{r}\) é um vetor unitário na direção da origem até o ponto de campo na superfície gaussiana.

(b) Campo em um ponto dentro da distribuição de carga. A superfície gaussiana agora está enterrada dentro da distribuição de carga, com\(r < R\). Portanto, somente as cargas na distribuição que estão dentro de uma distância r do centro da distribuição esférica de carga contam em\(r_{enc}\):

\[q_{enc} = \int_0^r ar'^n 4\pi r'^2 dr' = \dfrac{4\pi a}{n + 3} r^{n+3}. \nonumber\]

Agora, usando o resultado geral acima para\(\vec{E}_{in}\), encontramos o campo elétrico em um ponto que está a uma distância r do centro e está dentro da distribuição de carga como

\[\vec{E}_{in} = \left[ \dfrac{a}{\epsilon_0 ( n + 3)} \right] r^{n+1} \hat{r}, \nonumber\]

onde as informações de direção são incluídas usando o vetor radial unitário.

Exercício\(\PageIndex{1}\)

Verifique se os campos elétricos da esfera são reduzidos aos valores corretos para uma carga pontual.

Solução

Nesse caso, existe apenas\(\vec{E}_{out}\). Então, sim.

Distribuição de carga com simetria cilíndrica

Uma distribuição de carga tem simetria cilíndrica se a densidade de carga depender apenas da distância r do eixo de um cilindro e não deve variar ao longo do eixo ou com a direção em torno do eixo. Em outras palavras, se o sistema variar se você girá-lo em torno do eixo ou deslocá-lo ao longo do eixo, você não terá simetria cilíndrica.

A figura\(\PageIndex{7}\) mostra quatro situações em que as cargas são distribuídas em um cilindro. Uma densidade de carga uniforme\(\rho_0\) em um fio reto infinito tem uma simetria cilíndrica, assim como um cilindro infinitamente longo com densidade de carga constante\(\rho_0\). Um cilindro infinitamente longo que tem diferentes densidades de carga ao longo de seu comprimento, como uma densidade de carga\(\rho_1\)\(\rho_2 \neq \rho_1\) para\(z > 0\) e para\(z < 0\), não tem uma simetria cilíndrica utilizável para este curso. Nem um cilindro no qual a densidade de carga varia com a direção, como uma densidade de carga\(\rho_1\) para\(0 \leq \theta < \pi\) e\(\rho_2 \neq \rho_1\) para\(\pi \leq \theta < 2\pi\). Um sistema com conchas cilíndricas concêntricas, cada uma com densidades de carga uniformes, embora diferentes em conchas diferentes, como no FiFigure\(\PageIndex{7d}\), tem simetria cilíndrica se forem infinitamente longas. O requisito de comprimento infinito é devido à mudança da densidade de carga ao longo do eixo de um cilindro finito. Em sistemas reais, não temos cilindros infinitos; no entanto, se o objeto cilíndrico for consideravelmente maior do que o raio em que estamos interessados, a aproximação de um cilindro infinito se torna útil.

Figura\(\PageIndex{7}\): Para determinar se uma determinada distribuição de carga tem simetria cilíndrica, observe a seção transversal de um cilindro “infinitamente longo”. Se a densidade de carga não depender do ângulo polar da seção transversal ou ao longo do eixo, você terá simetria cilíndrica. (a) A densidade de carga é constante no cilindro; (b) a metade superior do cilindro tem uma densidade de carga diferente da metade inferior; (c) a metade esquerda do cilindro tem uma densidade de carga diferente da metade direita; (d) as cargas são constantes em diferentes anéis cilíndricos, mas a densidade não depende do polar ângulo. Os casos (a) e (d) têm simetria cilíndrica, enquanto (b) e (c) não.

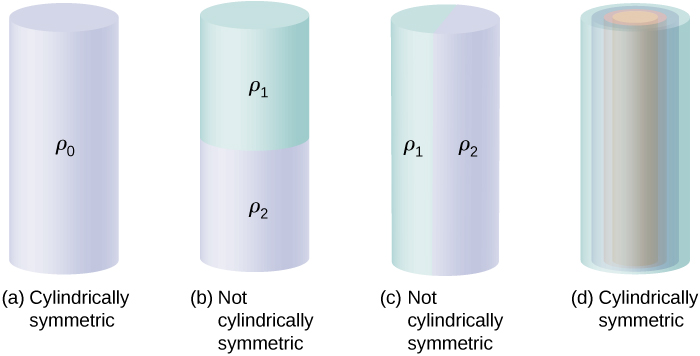
Consequências da assimetria

Em todos os casos cilíndricos simétricos, o campo elétrico\(E_p\) em qualquer ponto também\(P\) deve exibir simetria cilíndrica.

Simetria cilíndrica:\(\vec{E}_p = E_p(r)\hat{r}\), onde\(r\) é a distância do eixo e\(\hat{r}\) é um vetor unitário direcionado perpendicularmente para longe do eixo (Figura\(\PageIndex{8}\)).

Figura\(\PageIndex{8}\): O campo elétrico em uma situação cilíndricamente simétrica depende apenas da distância do eixo. A direção do campo elétrico é apontada para longe do eixo para cargas positivas e em direção ao eixo para cargas negativas.

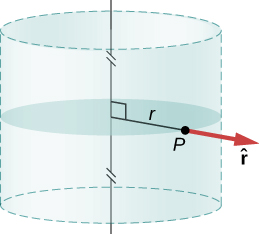
Cálculo gaussiano de superfície e fluxo

Para fazer uso da direção e da dependência funcional do campo elétrico, escolhemos uma superfície gaussiana fechada na forma de um cilindro com o mesmo eixo do eixo da distribuição de carga. O fluxo através dessa superfície de raio s e altura L é fácil de calcular se dividirmos nossa tarefa em duas partes: (a) um fluxo através das extremidades planas e (b) um fluxo através da superfície curva (Figura\(\PageIndex{9}\)).

Figura\(\PageIndex{9}\): A superfície gaussiana no caso da simetria cilíndrica. O campo elétrico em uma mancha é paralelo ou perpendicular ao normal à mancha da superfície gaussiana.

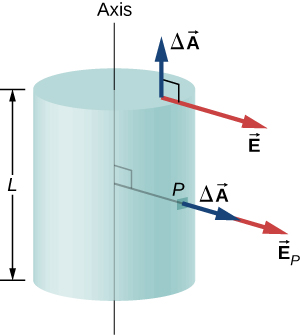
O campo elétrico é perpendicular ao lado cilíndrico e paralelo às extremidades planas da superfície. O fluxo através da parte cilíndrica é

\[\int_S \vec{E} \cdot \hat{n} dA = E \int_S dA = E(2\pi r L), \nonumber\]

enquanto o fluxo através das tampas é zero porque\(\vec{E} \cdot \hat{n} = 0\) existe. Assim, o fluxo é

\[\int_S \vec{E} \cdot \hat{n} dA = E(2\pi rL) + 0 + 0 = 2\pi rLE. \nonumber\]

Usando a lei de Gauss

De acordo com a lei de Gauss, o fluxo deve ser igual à quantidade de carga dentro do volume fechado por essa superfície, dividida pela permissividade do espaço livre. Quando você faz o cálculo de um cilindro de comprimento L, você descobre que a lei\(q_{enc}\) de Gauss é diretamente proporcional a L. Vamos escrevê-lo como carga por unidade de comprimento (\(\lambda_{enc}\)) vezes comprimento L:

\[q_{enc} = \lambda_{enc} L.\]

Portanto, a lei de Gauss para qualquer distribuição de carga cilíndricamente simétrica produz a seguinte magnitude do campo elétrico a uma distância s do eixo:

\[Magnitude: \, E(r) = \dfrac{\lambda_{enc}}{2\pi \epsilon_0} \dfrac{1}{r}.\]

A carga por unidade de comprimento\(\lambda_{enc}\) depende se o ponto de campo está dentro ou fora do cilindro de distribuição de carga, assim como vimos na distribuição esférica.

Computando a carga fechada

Seja R o raio do cilindro dentro do qual as cargas são distribuídas de forma cilíndricamente simétrica. Deixe o ponto de campo P estar a uma distância s do eixo. (O lado da superfície gaussiana inclui o ponto de campo P.) Quando\(r > R\) (ou seja, quando P está fora da distribuição de carga), a superfície gaussiana inclui toda a carga no cilindro de raio R e comprimento L. Quando\(r < R\) (P está localizado dentro da distribuição de carga), somente a carga dentro de um cilindro de raio s e comprimento L é delimitada pela superfície gaussiana:

\(\lambda_{enc} = (total \, charge) \, if \, r \geq R\)

\(\lambda_{enc} = (only \, charge \, within \, t < R) \, if \, r < R\)

Concha cilíndrica uniformemente carregada

Uma concha cilíndrica não condutora muito longa de raio R tem uma densidade de carga superficial uniforme.\(\sigma_0\) Encontre o campo elétrico (a) em um ponto fora da concha e (b) em um ponto dentro da concha.

Estratégia

Aplique a estratégia da lei de Gauss dada anteriormente, onde tratamos os casos dentro e fora da concha separadamente.

Solução

a. Campo elétrico em um ponto fora da casca. Para um ponto fora da concha cilíndrica, a superfície gaussiana é a superfície de um cilindro de raio\(r > R\) e comprimento L, conforme mostrado na Figura\(\PageIndex{10}\). A carga envolvida pelo cilindro gaussiano é igual à carga no invólucro cilíndrico de comprimento L. Portanto,\(\lambda_{enc}\) é dado por\[\lambda_{enc} = \dfrac{\sigma_0 2\pi RL}{L} = 2\pi R \sigma_0.\]

Figura\(\PageIndex{10}\): Uma superfície gaussiana ao redor de uma concha cilíndrica.

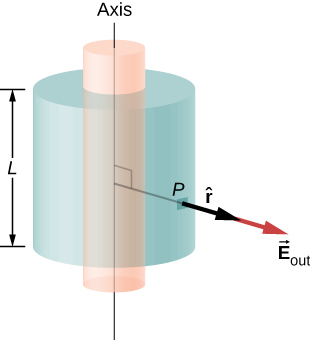
Portanto, o campo elétrico em um ponto P fora da concha a uma distância r longe do eixo é

\[\vec{E} = \dfrac{2\pi R \sigma_0}{2 \pi \epsilon_0} \dfrac{1}{r} \hat{r} = \dfrac{R\sigma_0}{\epsilon_0} \dfrac{1}{r} \hat{r} \, (r > R)\]

onde\(\hat{r}\) está um vetor unitário, perpendicular ao eixo e apontando para longe dele, conforme mostrado na figura. O campo elétrico em P aponta na direção\(\hat{r}\) dada na Figura\(\PageIndex{10}\) if\(\sigma_0 > 0\) e na direção oposta a\(\hat{r}\) if\(\sigma_0 <0\).

b. Campo elétrico em um ponto dentro da casca. Para um ponto dentro da concha cilíndrica, a superfície gaussiana é um cilindro cujo raio r é menor que R (Figura\(\PageIndex{11}\)). Isso significa que nenhuma carga está incluída dentro da superfície gaussiana:

\[\lambda_{enc} = 0.\]

Figura\(\PageIndex{11}\): Uma superfície gaussiana dentro de uma concha cilíndrica.

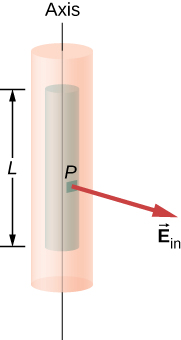
Isso fornece a seguinte equação para a magnitude do campo elétrico\(E_{in}\) em um ponto cujo r é menor que R da camada de cargas.

\[E_{in} 2\pi rL = 0 (r<R), \nonumber\]

Isso nos dá

\[E_{in} = 0 (r < R). \nonumber\]

Significância

Observe que o resultado dentro do invólucro é exatamente o que devemos esperar: nenhuma carga fechada significa campo elétrico zero. Fora do invólucro, o resultado se torna idêntico a um fio com carga uniforme\(R\sigma\).

Exercício\(\PageIndex{2}\)

Um fio reto fino tem uma densidade de carga linear uniforme\(\lambda_0\). Encontre o campo elétrico a uma distância d do fio, onde d é muito menor que o comprimento do fio.

Solução

\(\vec{E} = \frac{\lambda_0}{2\pi \epsilon_0} \frac{1}{d} \hat{r}\); Isso concorda com o cálculo de [link], onde encontramos o campo elétrico integrando o fio carregado. Observe como o cálculo desse campo elétrico é muito mais simples com a lei de Gauss.

Distribuição de carga com simetria planar

Uma simetria plana da densidade de carga é obtida quando as cargas são distribuídas uniformemente sobre uma grande superfície plana. Em simetria plana, todos os pontos em um plano paralelo ao plano de carga são idênticos em relação às cargas.

Consequências da simetria

Consideramos que o plano da distribuição de carga é o plano xy e encontramos o campo elétrico em um ponto espacial P com coordenadas (x, y, z). Como a densidade de carga é a mesma em todas as coordenadas (x, y) no\(z = 0\) plano, por simetria, o campo elétrico em P não pode depender das coordenadas x ou y do ponto P, conforme mostrado na Figura\(\PageIndex{12}\). Portanto, o campo elétrico em P só pode depender da distância do avião e tem uma direção em direção ao plano ou longe do plano. Ou seja, o campo elétrico em P tem apenas um componente z diferente de zero.

Cargas uniformes no plano xy:\(\vec{E} = E(z) \hat{z}\) onde z é a distância do plano e\(\hat{z}\) é o vetor unitário normal ao plano. Observe que neste sistema, embora\(E(z) = E(-z)\), é claro, eles apontem em direções opostas.

Figura\(\PageIndex{12}\): Os componentes do campo elétrico paralelo a um plano de cargas cancelam as duas cargas localizadas simetricamente a partir do ponto de campo P. Portanto, o campo em qualquer ponto é apontado verticalmente a partir do plano de cargas. Para qualquer ponto P e carga\(q_1\), sempre podemos encontrar um\(q_2\) com esse efeito.

Cálculo gaussiano de superfície e fluxo

No presente caso, uma superfície gaussiana conveniente é uma caixa, pois o campo elétrico esperado aponta apenas em uma direção. Para manter a caixa gaussiana simétrica em relação ao plano de cargas, nós a usamos para atravessar o plano das cargas, de forma que uma face contendo o ponto de campo P seja levada paralelamente ao plano das cargas. Na Figura\(\PageIndex{13}\), os lados I e II da superfície gaussiana (a caixa) que são paralelos ao plano infinito foram sombreados. Eles são as únicas superfícies que dão origem a um fluxo diferente de zero porque o campo elétrico e os vetores de área das outras faces são perpendiculares entre si.

Figura\(\PageIndex{13}\): Uma fina folha carregada e a caixa gaussiana para encontrar o campo elétrico no ponto de campo P. O normal para cada face da caixa é de dentro para fora da caixa. Nas duas faces da caixa, os campos elétricos são paralelos aos vetores de área e, nas outras quatro faces, os campos elétricos são perpendiculares aos vetores de área.

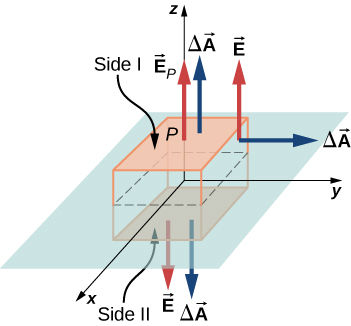
Seja A a área da superfície sombreada em cada lado do plano e E P

seja a magnitude do campo elétrico no ponto P. Como os lados I e II estão à mesma distância do plano, o campo elétrico tem a mesma magnitude em pontos desses planos, embora as direções do campo elétrico nesses pontos nos dois planos sejam opostas uma à outra.

Magnitude em I ou II:\(E(z) = E_p\).

Se a carga no avião for positiva, a direção do campo elétrico e os vetores de área serão mostrados na Figura\(\PageIndex{13}\). Portanto, encontramos o fluxo de campo elétrico através da caixa

\[\Phi = \int_S \vec{E}_p \cdot \hat{n} dA = E_pA + E_pA + 0 + 0 + 0 + 0 = 2E_p A\]

onde os zeros são para o fluxo através dos outros lados da caixa. Observe que, se a carga no avião for negativa, as direções do campo elétrico e os vetores de área dos planos I e II são opostas uma à outra, e obtemos um sinal negativo para o fluxo. De acordo com a lei de Gauss, o fluxo deve ser igual\(q_{enc}/\epsilon_0\). Na Figura\(\PageIndex{13}\), vemos que as cargas dentro do volume fechado pela caixa gaussiana residem na área A do plano xy. Conseqüentemente,

\[q_{enc} = \sigma_0 A. \nonumber\]

Usando as equações para o fluxo e a carga fechada na lei de Gauss, podemos determinar imediatamente o campo elétrico em um ponto na altura z a partir de um plano uniformemente carregado no plano xy:

\[\vec{E}_p = \dfrac{\sigma_0}{2\epsilon_0} \hat{n}. \nonumber\]

A direção do campo depende do sinal da carga no plano e do lado do plano onde o ponto de campo P está localizado. Observe que acima do avião,\(\hat{n} = + \hat{z}\), enquanto abaixo do plano,\(\hat{n} = - \hat{z}\).

Você pode se surpreender ao notar que o campo elétrico não depende realmente da distância do avião; isso é um efeito da suposição de que o plano é infinito. Em termos práticos, o resultado dado acima ainda é uma aproximação útil para planos finitos próximos ao centro.