6.2: Fluxo elétrico
- Page ID
- 184585
Ao final desta seção, você poderá:
- Defina o conceito de fluxo
- Descreva o fluxo elétrico
- Calcule o fluxo elétrico para uma determinada situação
O conceito de fluxo descreve quanto de algo passa por uma determinada área. Mais formalmente, é o produto escalar de um campo vetorial (neste capítulo, o campo elétrico) com uma área. Você pode conceituar o fluxo de um campo elétrico como uma medida do número de linhas de campo elétrico passando por uma área (Figura\(\PageIndex{1}\)). Quanto maior a área, mais linhas de campo passam por ela e, portanto, maior o fluxo; da mesma forma, quanto mais forte for o campo elétrico (representado por uma maior densidade de linhas), maior será o fluxo. Por outro lado, se a área girar de forma que o plano fique alinhado com as linhas do campo, nenhuma passará e não haverá fluxo.
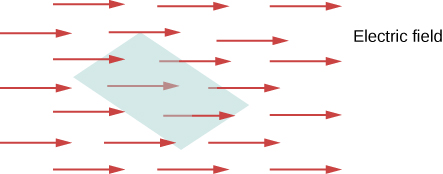
Uma analogia macroscópica que pode ajudar você a imaginar isso é colocar um bambolê em um rio que corre. Conforme você altera o ângulo do aro em relação à direção da corrente, mais ou menos do fluxo passará pelo aro. Da mesma forma, a quantidade de fluxo através do aro depende da força da corrente e do tamanho do aro. Novamente, fluxo é um conceito geral; também podemos usá-lo para descrever a quantidade de luz solar que atinge um painel solar ou a quantidade de energia que um telescópio recebe de uma estrela distante, por exemplo.
Para quantificar essa ideia, a Figura\(\PageIndex{1a}\) mostra uma superfície plana\(S_1\) de área\(A_1\) que é perpendicular ao campo elétrico uniforme\(\vec{E} = E\hat{y}\). Se N linhas de campo passarem\(S_1\), então sabemos pela definição de linhas de campo elétrico (cargas e campos elétricos) que\(N/A \propto E\), ou\(N \propto EA_1\).
A quantidade\(EA_1\) é o fluxo elétrico que passa\(S_1\). Representamos o fluxo elétrico através de uma superfície aberta, como\(S_1\) no símbolo\(\Phi\). O fluxo elétrico é uma grandeza escalar e tem uma unidade SI de newton-metros quadrados por coulomb (\(N \cdot m^2/C\)). Observe que também\(N \propto EA_1\) pode ser escrito como\(N \propto \Phi\), demonstrando que o fluxo elétrico é uma medida do número de linhas de campo que cruzam uma superfície.
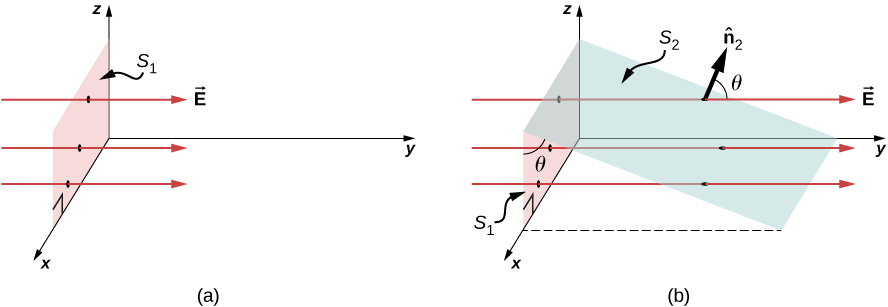
Agora, considere uma superfície plana que não seja perpendicular ao campo. Como representaríamos o fluxo elétrico? \(\PageIndex{2b}\)A figura mostra uma superfície\(S_2\) de área\(A_2\) que está inclinada em um ângulo\(\theta\) com o plano xz e cuja projeção nesse plano é\(S_1\) (área\(A_1\)). As áreas estão relacionadas por\(A_2 \, cos \, \theta = A_1\). Como o mesmo número de linhas de campo cruza as duas\(S_1\) e\(S_2\), os fluxos pelas duas superfícies devem ser os mesmos. O fluxo através\(S_2\) é, portanto\(\Phi = EA_1 = EA_2 \, cos \, \theta\). Designando\(\hat{n}_2\) como um vetor unitário normal para\(S_2\) (veja a Figura\(\PageIndex{2b}\)), obtemos
\[\Phi = \vec{E} \cdot \hat{n}_2 A_2.\]
Confira este vídeo para observar o que acontece com o fluxo à medida que a área muda de tamanho e ângulo, ou o campo elétrico muda de intensidade.
Vetor de área
Para discutir o fluxo de um campo vetorial, é útil introduzir um vetor de área\(\vec{A}\). Isso nos permite escrever a última equação de uma forma mais compacta. Qual deve ser a magnitude do vetor de área? Qual deve ser a direção do vetor de área? Quais são as implicações de como você responde à pergunta anterior?
O vetor de área de uma superfície plana da área A tem a seguinte magnitude e direção:
- A magnitude é igual à área (A)
- A direção é ao longo do normal até a superfície\((\hat{n})\); isto é, perpendicular à superfície.
Como a superfície normal a uma superfície plana pode apontar em qualquer direção da superfície, a direção do vetor de área de uma superfície aberta precisa ser escolhida, conforme mostrado na Figura\(\PageIndex{3}\).
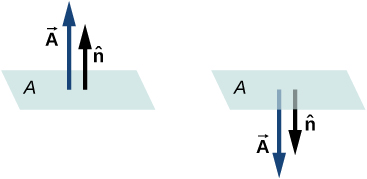
Como\(\hat{n}\) é uma unidade normal para uma superfície, ela tem duas direções possíveis em cada ponto dessa superfície (Figura\(\PageIndex{1a}\)). Para uma superfície aberta, podemos usar qualquer direção, desde que sejamos consistentes em toda a superfície. \(\PageIndex{1c}\)da figura mostra vários casos.
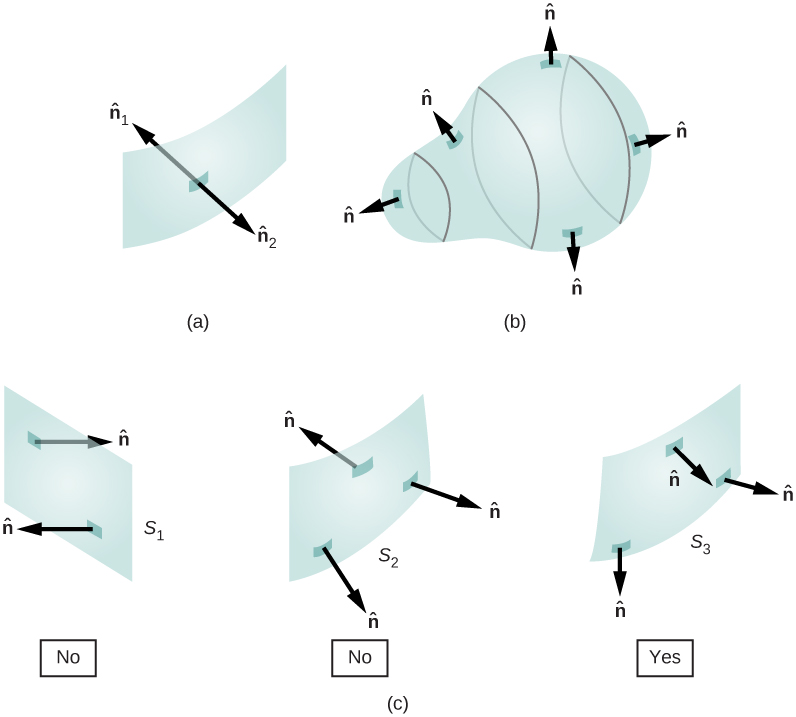
No entanto, se uma superfície estiver fechada, ela incluirá um volume. Nesse caso, a direção do vetor normal em qualquer ponto da superfície aponta de dentro para fora. Em uma superfície fechada, como a da Figura\(\PageIndex{1b}\),\(\hat{n}\) é escolhido para ser o normal externo em todos os pontos, para ser consistente com a convenção de sinalização para carga elétrica.
Fluxo elétrico
Agora que definimos o vetor de área de uma superfície, podemos definir o fluxo elétrico de um campo elétrico uniforme através de uma área plana como o produto escalar do campo elétrico e o vetor de área:
\[\Phi = \vec{E} \cdot \vec{A} \, (uniform \, \hat{E}, \, flat \, surface).\]
A figura\(\PageIndex{5}\) mostra o campo elétrico de um sistema de placa paralela com carga oposta e uma caixa imaginária entre as placas. O campo elétrico entre as placas é uniforme e aponta da placa positiva em direção à placa negativa. Um cálculo do fluxo desse campo através de várias faces da caixa mostra que o fluxo líquido através da caixa é zero. Por que o fluxo se cancela aqui?
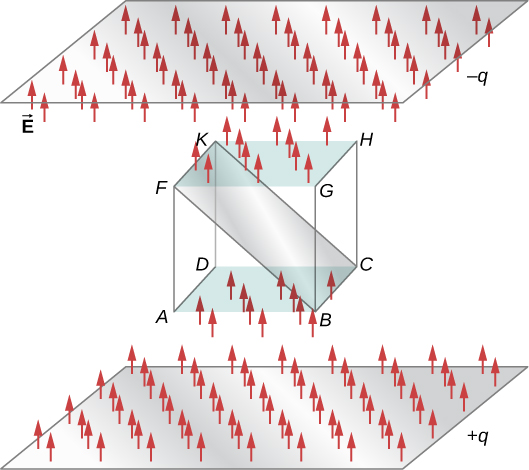
O motivo é que as fontes do campo elétrico estão fora da caixa. Portanto, se alguma linha de campo elétrico entrar no volume da caixa, ela também deverá sair em algum lugar da superfície, pois não há carga interna para que as linhas caiam. Portanto, geralmente, o fluxo elétrico através de uma superfície fechada é zero se não houver fontes de campo elétrico, sejam cargas positivas ou negativas, dentro do volume fechado. Em geral, quando as linhas de campo saem (ou “fluem para fora”) de uma superfície fechada,\(\Phi\) é positivo; quando elas entram (ou “fluem para dentro”) da superfície,\(\Phi\) é negativo.
Qualquer superfície lisa e não plana pode ser substituída por uma coleção de superfícies pequenas e aproximadamente planas, conforme mostrado na Figura\(\PageIndex{6}\). Se dividirmos uma superfície S em pequenas manchas, notamos que, à medida que as manchas se tornam menores, elas podem ser aproximadas por superfícies planas. Isso é semelhante à forma como tratamos a superfície da Terra como localmente plana, embora saibamos que, globalmente, ela é aproximadamente esférica.
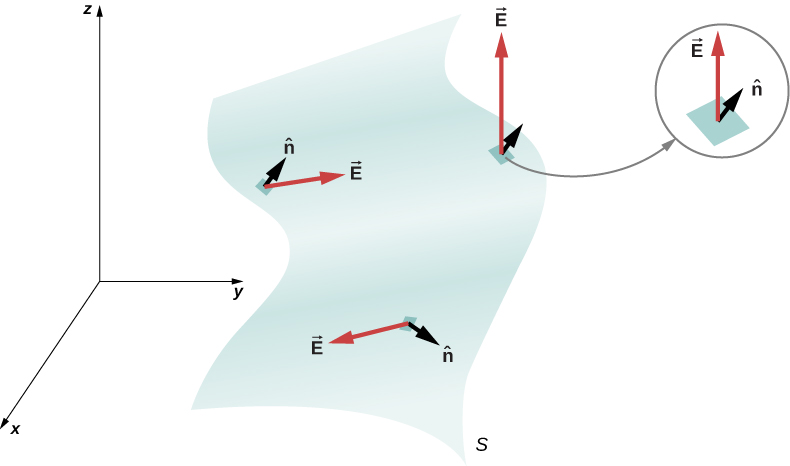
Para acompanhar os patches, podemos numerá-los de 1 a N. Agora, definimos o vetor de área para cada mancha como a área da mancha apontada na direção do normal. Vamos denotar o vetor de área para o i th patch by\(\delta \vec{A}_i\). (Usamos o símbolo\(\delta\) para nos lembrar que a área é de uma mancha arbitrariamente pequena.) Com manchas suficientemente pequenas, podemos aproximar o campo elétrico de qualquer mancha como uniforme. Vamos denotar o campo elétrico médio na localização do no patch by\(\vec{E}_i\).
\[\vec{E}_i = \mathrm{average \, electric \, field \, over \, the \,} i \mathrm{th \, patch}.\]
Portanto, podemos escrever o fluxo elétrico\(\Phi\) através da área do patch como
\[\Phi_i = \vec{E}_i \cdot \delta \vec{A}_i \, (i \mathrm{th \, patch}).\]
O fluxo através de cada uma das manchas individuais pode ser construído dessa maneira e, em seguida, adicionado para nos dar uma estimativa do fluxo líquido através de toda a superfície S, que denotamos simplesmente como\(\Phi\).
\[\Phi = \sum_{i=1}^N \Phi_i = \sum_{i=1}^N \vec{E}_i \cdot \delta \vec{A}_i \, (N \, patch \, estimate).\]
Essa estimativa do fluxo melhora à medida que diminuímos o tamanho das manchas. No entanto, quando você usa manchas menores, você precisa de mais delas para cobrir a mesma superfície. No limite de manchas infinitesimalmente pequenas, elas podem ser consideradas como tendo área dA e unidade normal\(\hat{n}\). Como os elementos são infinitesimais, eles podem ser considerados planos e\(\vec{E}_i\) podem ser considerados constantes sobre qualquer elemento. Em seguida, o fluxo\(d\Phi\) através de uma área dA é dado por\(d\Phi = \vec{E} \cdot \hat{n} dA\). É positivo quando o ângulo entre\(\vec{E}_i\) e\(\hat{n}\) é menor que\(90^o\) e negativo quando o ângulo é maior que\(90^o\). O fluxo líquido é a soma dos elementos do fluxo infinitesimal em toda a superfície. Com manchas infinitesimalmente pequenas, você precisa de infinitas manchas, e o limite da soma se torna uma integral da superfície. Com a\(\int_S\) representação da integral sobre S,
\[\Phi = \int_S \vec{E} \cdot \hat{n}dA = \int_S \vec{E} \cdot d\vec{A} \, (open \, surface).\]
Em termos práticos, as integrais de superfície são calculadas tomando as antiderivadas de ambas as dimensões que definem a área, com as bordas da superfície em questão sendo os limites da integral.
Para distinguir entre o fluxo através de uma superfície aberta como a da Figura\(\PageIndex{2}\) e o fluxo através de uma superfície fechada (que limita completamente algum volume), representamos o fluxo através de uma superfície fechada por
\[\Phi = \oint_S \vec{E} \cdot \hat{n} dA = \oint_S \vec{E} \cdot d\vec{A} \, (closed \, surface)\]
onde o círculo através do símbolo integral significa simplesmente que a superfície está fechada e estamos nos integrando sobre a coisa toda. Se você se integra apenas sobre uma parte de uma superfície fechada, isso significa que você está tratando um subconjunto dela como uma superfície aberta.
Um campo elétrico constante de magnitude\(E_0\) aponta na direção do eixo z positivo (Figura\(\PageIndex{7}\)). Qual é o fluxo elétrico através de um retângulo com os lados a e b no plano (a) xy e no plano (b) xz?
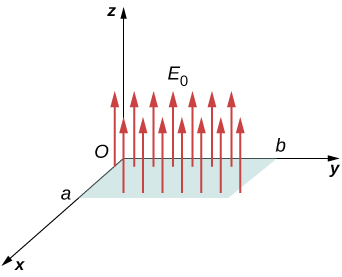
Estratégia
Aplique a definição de fluxo:\(\Phi = \vec{E} \cdot \vec{A} \, (uniform \, \vec{E})\), onde a definição de produto escalar é crucial.
Solução
- Nesse caso,\(\Phi = \vec{E}_0 \cdot \vec{A} = E_0 A = E_0 ab\).
- Aqui, a direção do vetor de área é ao longo do eixo y positivo ou em direção ao eixo y negativo. Portanto, o produto escalar do campo elétrico com o vetor de área é zero, dando fluxo zero.
Significância
As direções relativas do campo elétrico e da área podem fazer com que o fluxo através da área seja zero.
Um campo elétrico constante de magnitude\(E_0\) aponta na direção do eixo z positivo (Figura\(\PageIndex{8}\)). Qual é o fluxo elétrico líquido através de um cubo?

Estratégia
Aplique a definição de fluxo:\(\Phi = \vec{E} \cdot \vec{A} \, (uniform \, \vec{E})\), observando que uma superfície fechada elimina a ambigüidade na direção do vetor de área.
Solução
Através da face superior do cubo\(\Phi = \vec{E}_0 \cdot \vec{A} = E_0 A\).
Através da face inferior do cubo,\(\Phi = \vec{E}_0 \cdot \vec{A} = - E_0 A\), porque o vetor de área aqui aponta para baixo.
Nos outros quatro lados, a direção do vetor de área é perpendicular à direção do campo elétrico. Portanto, o produto escalar do campo elétrico com o vetor de área é zero, dando fluxo zero.
O fluxo líquido é\(\Phi_{net} = E_0A - E_0 A + 0 + 0 + 0 + 0 = 0\).
Significância
O fluxo líquido de um campo elétrico uniforme através de uma superfície fechada é zero.
Um campo elétrico uniforme\(\vec{E}\) de magnitude 10 N/C é direcionado paralelamente ao plano yz\(30^o\) acima do plano xy, conforme mostrado na Figura\(\PageIndex{9}\). Qual é o fluxo elétrico através da superfície plana da área\(6.0 \, m^2\) localizada no plano xz? Suponha que\(\hat{n}\) aponte na direção y positiva.
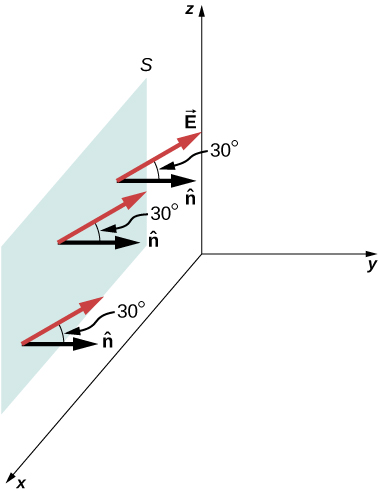
Estratégia
Aplique\(\Phi = \int_S \vec{E} \cdot \hat{n} dA\), onde a direção e a magnitude do campo elétrico são constantes.
Solução
O ângulo entre o campo elétrico uniforme\(\vec{E}\) e a unidade normal em relação\(\hat{n}\) à superfície plana é\(30^o\). Como a direção e a magnitude são constantes, E sai da integral. Tudo o que resta é uma superfície integral sobre dA, que é A. Portanto, usando a equação de superfície aberta, descobrimos que o fluxo elétrico através da superfície é
\[\Phi = \int_S \vec{E} \cdot \hat{n} dA = EA \, cos \, \theta\]
\[= (10 \, N/C)(6.0 \, m^2)(cos \, 30^o) = 52 \, N \cdot m^2/C.\]
Significância
Novamente, as direções relativas do campo e da área são importantes, e a equação geral com a integral se simplificará para o produto escalar simples da área e do campo elétrico.
Qual ângulo deve haver entre o campo elétrico e a superfície mostrada\(\PageIndex{9}\) na Figura no exemplo anterior para que nenhum fluxo elétrico passe pela superfície?
Solução
Posicione-o de forma que sua unidade normal fique perpendicular\(\vec{E}\) a.
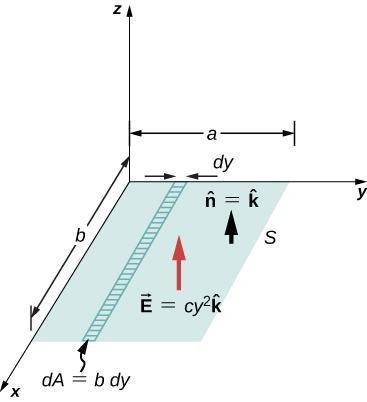
Qual é o fluxo total do campo elétrico\(\vec{E} = cy^2\hat{k}\) através da superfície retangular mostrada na Figura\(\PageIndex{10}\)?
Estratégia
Aplique\(\Phi = \int_S \vec{E} \cdot \hat{n}dA\). Assumimos que a unidade normal\(\hat{n}\) para a superfície dada aponta na direção z positiva, então\(\hat{n} = \hat{k}\). Como o campo elétrico não é uniforme sobre a superfície, é necessário dividir a superfície em faixas infinitesimais ao longo das quais\(\vec{E}\) seja essencialmente constante. Conforme mostrado na Figura\(\PageIndex{10}\), essas faixas são paralelas ao eixo x e cada faixa tem uma área\(dA = b \, dy\).
Solução
A partir da integral da superfície aberta, descobrimos que o fluxo líquido através da superfície retangular é
\[\begin{align*} \Phi &= \int_S \vec{E} \cdot \hat{n} dA = \int_0^a (cy^2 \hat{k}) \cdot \hat{k}(b \, dy) \\[4pt] &= cb \int_0^a y^2 dy = \frac{1}{3} a^3 bc. \end{align*}\]
Significância
Para um campo elétrico não constante, o método integral é necessário.
Se o campo elétrico no Exemplo\(\PageIndex{4}\) for\(\vec{E} = mx\hat{k}\). qual é o fluxo através da área retangular?
Solução
\(mab^2/2\)


