7.5: A partícula quântica em uma caixa
- Page ID
- 183284
Ao final desta seção, você poderá:
- Descreva como configurar um problema de valor limite para a equação estacionária de Schrdinger
- Explique por que a energia de uma partícula quântica em uma caixa é quantizada
- Descreva o significado físico das soluções estacionárias para a equação de SchrDinger e a conexão dessas soluções com estados quânticos dependentes do tempo
- Explique o significado físico do princípio da correspondência de Bohr
Nesta seção, aplicamos a equação de SchrDinger a uma partícula vinculada a uma caixa unidimensional. Este caso especial fornece lições para entender a mecânica quântica em sistemas mais complexos. A energia da partícula é quantizada como consequência de uma condição de onda estacionária dentro da caixa.
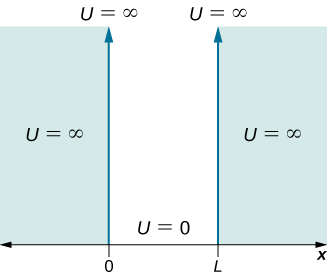
Considere uma partícula de massa\(m\) que pode se mover somente ao longo da direção x e seu movimento está confinado à região entre paredes rígidas e rígidas localizadas em\(x = 0\) e em\(x = L\) (Figura\(\PageIndex{1}\)). Entre as paredes, a partícula se move livremente. Essa situação física é chamada de poço quadrado infinito, descrita pela função de energia potencial
\ [U (x) =\ begin {casos}
0 e 0\ leq x\ leq L\\
\ infty & x< 0\; and\; x> L\ end {casos}\ label {3.5.2}\]
A combinação dessa equação com a equação de onda independente do tempo de SchrDinger fornece
\[\dfrac{-\hbar^2}{2m} \dfrac{d^2\psi(x)}{dx^2} = E\psi(x), \, for \, 0 \leq x \leq L \label{7.32} \]
onde\(E\) está a energia total da partícula. Que tipos de soluções esperamos? A energia da partícula é um número positivo, portanto, se o valor da função de onda for positivo (lado direito da equação), a curvatura da função de onda será negativa ou côncava para baixo (lado esquerdo da equação). Da mesma forma, se o valor da função de onda for negativo (lado direito da equação), a curvatura da função de onda será positiva ou côncava para cima (lado esquerdo da equação). Essa condição é atendida por uma função de onda oscilante, como uma onda senoidal ou cosseno. Como essas ondas estão confinadas à caixa, imaginamos ondas estacionárias com pontos finais fixos em\(x = 0\)\(x = L\) e.
As soluções\(\psi(x)\) para essa equação têm uma interpretação probabilística. Em particular, o quadrado\(|\psi(x)|^2\) representa a densidade de probabilidade de encontrar a partícula em um determinado local x. Essa função deve ser integrada para determinar a probabilidade de encontrar a partícula em algum intervalo de espaço. Portanto, estamos procurando uma solução normalizável que satisfaça a seguinte condição de normalização:
\[\int_0^L dx|\psi(x)|^2 = 1. \label{7.33} \]
As paredes são rígidas e impenetráveis, o que significa que a partícula nunca é encontrada além da parede. Matematicamente, isso significa que a solução deve desaparecer nas paredes:
\[\psi(0) = \psi(L) = 0. \label{7.34} \]
Esperamos soluções oscilantes, então a solução mais geral para essa equação é
\[\psi_k(x) = A_k \, \cos \, kx + B_k \, \sin \, kx \label{7.35} \]
onde\(k\) está o número da onda\(A_k\) e e\(B_k\) são constantes. A aplicação da condição de contorno expressa pela Equação\ ref {7.33} dá
\[\psi_k(0) = A_k \, \cos (k \cdot 0) + B_k \, \sin (k \cdot 0) = A_k = 0. \label{7.36} \]
Porque temos\(A_k = 0\), a solução deve ser
\[\psi_k(x) = B_k \, \sin \, kx. \label{7.37} \]
Se\(B_k\) for zero, então\(\psi_k(x) = 0\) para todos os valores\(x\) e a condição de normalização (Equação\ ref {7.33}) não pode ser satisfeita. Supondo que\(B_k \neq 0\) a Equação\ ref {7.34} para\(x = L\) então forneça
\[0 = B_k \, \sin (kL) \Rightarrow \sin(kL) = 0 \Rightarrow kL = n\pi, \, n = 1,2,3,... \label{7.38} \]
Nós descartamos a\(n = 0\) solução porque\(\psi(x)\) esse número quântico seria zero em todos os lugares — uma solução não normalizável e, portanto, não física. Substituindo a Equação\ ref {7.37} pela Equação\ ref {7.32} dá
\[-\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2} (B_k \sin(kx)) = E(B_k \sin(kx)). \label{7.39} \]
A computação desses derivados leva a
\[E = E_k = \dfrac{\hbar^2k^2}{2m}. \label{7.40} \]
De acordo com de Broglie\(p = \hbar k\),, essa expressão implica que a energia total é igual à energia cinética, consistente com nossa suposição de que a “partícula se move livremente”. A combinação dos resultados da Equação\ ref {7.38} e\ ref {7.40} dá
\[E_n = n^2 \dfrac{\pi^2 \hbar^2}{2mL^2}, \, n = 1,2,3,... \label{7.41} \]
A equação\ ref {7.41} argumenta que uma partícula ligada a uma caixa unidimensional só pode ter certos valores discretos (quantizados) de energia. Além disso, a partícula não pode ter energia cinética zero — é impossível que uma partícula amarrada a uma caixa fique “em repouso”.
Para avaliar as funções de onda permitidas que correspondem a essas energias, devemos encontrar a constante de normalização\(B_n\). Impomos a condição de normalização Equation\ ref {7.33} na função de onda
\[\psi_n(x) = B_n \, \sin \, \dfrac{n\pi x}{L} \label{7.42} \]
Começamos com a condição de normalização (Equação\ ref {7.33})
\[\begin{align} 1 &= \int_0^L dx|\psi_n(x)|^2 \\[5pt] &= \int_0^L dx \, B_n^2 \, \sin^2 \dfrac{n\pi}{L} x \\[5pt] &= B^2 n \int_0^2 dx \, \sin^2 \dfrac{n\pi}{L}x \\[5pt] &= B_n^2 \dfrac{L}{2} \\[5pt] \Rightarrow B_n &= \sqrt{\dfrac{2}{L}}. \end{align} \nonumber \]
Portanto, as funções de onda que correspondem aos valores de energia dados na Equação\ ref {7.41} são
\[\psi_n(x) = \sqrt{\dfrac{2}{L}} \, \sin \, \dfrac{n\pi x}{L}, \, n = 1,2,3,... \label{7.43} \]
Para o estado de energia mais baixo ou energia do estado fundamental, temos
\[E_1 = \dfrac{\pi^2 \hbar^2}{2mL^2}, \, \psi_1(x) = \sqrt{\dfrac{2}{L}} \, \sin \left(\dfrac{\pi x}{L}\right). \label{7.44} \]
Todos os outros estados de energia podem ser expressos como
\[E_n = n^2 E_1, \, \psi_n(x) = \sqrt{\dfrac{2}{L}} \, \sin \, \left(\dfrac{n\pi x}{L}\right). \label{7.45} \]
O índice\(n\) é chamado de número quântico de energia ou número quântico principal. O estado para\(n = 2\) é o primeiro estado excitado, o estado para\(n = 3\) é o segundo estado excitado e assim por diante. Os primeiros três estados quânticos (para n = 1, 2 e 3) de uma partícula em uma caixa são mostrados na Figura\(\PageIndex{2}\). As funções de onda na Equação\ ref {7.45} às vezes são chamadas de “estados de energia definida”. Diz-se que as partículas nesses estados ocupam níveis de energia, representados pelas linhas horizontais na Figura\(\PageIndex{2}\). Os níveis de energia são análogos aos degraus de uma escada que a partícula pode “subir” à medida que ganha ou perde energia.
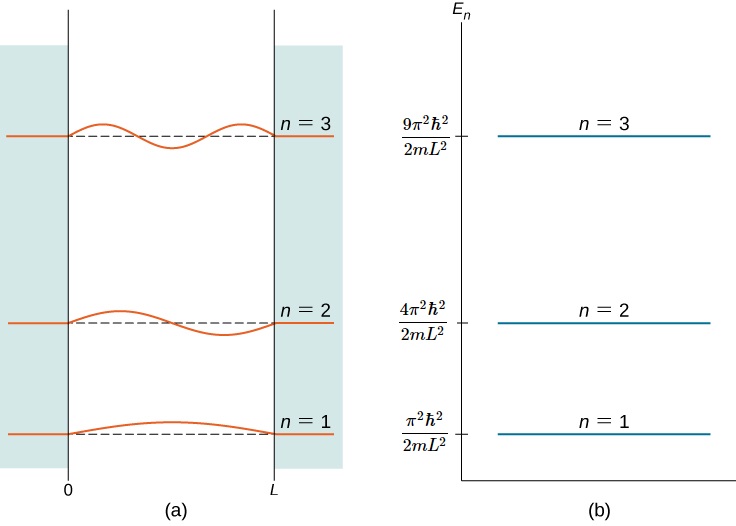
As funções de onda na Equação\ ref {7.45} também são chamadas de estados estacionários e estados de onda estacionária. Essas funções são “estacionárias”, porque suas funções de densidade de probabilidade não variam no tempo, e “ondas estacionárias” porque suas partes reais e imaginárias oscilam para cima e para baixo como uma onda estacionária — como uma corda acenando entre duas crianças em um parquinho.\(|\Psi(x,t)|^2\) Estados estacionários são estados de energia definida (Equação\ ref {7.45}), mas combinações lineares desses estados, como\(\psi(x) = a\psi_1 + b\psi_2\) (também soluções para a equação de SchrDinger) são estados de energia mista.
A quantização de energia é uma consequência das condições de contorno. Se a partícula não estiver confinada a uma caixa, mas vagar livremente, as energias permitidas são contínuas. No entanto, neste caso, somente certas energias (\(E_1, 4E_1, 9E_1,...\)) são permitidas. A diferença de energia entre os níveis de energia adjacentes é dada por
\[\Delta E_{n+1,n} = E_{n+1} - E_n = (n + 1)^2 E_1 - n^2E_1 = (2n + 1) E_1. \nonumber \]
A conservação da energia exige que, se a energia do sistema mudar, a diferença de energia seja transportada em alguma outra forma de energia. Para o caso especial de uma partícula carregada confinada a um pequeno volume (por exemplo, em um átomo), as mudanças de energia geralmente são provocadas por fótons. As frequências dos fótons emitidos nos fornecem informações sobre as diferenças de energia (espaçamentos) do sistema e o volume de contenção — o tamanho da “caixa” (Equação\ ref {7.44}).
Suponha que um próton esteja confinado a uma caixa de largura\(L = 1.00 \times 10^{-14} m\) (um raio nuclear típico). Quais são as energias do solo e os primeiros estados de excitação? Se o próton fizer uma transição do primeiro estado excitado para o estado fundamental, quais são a energia e a frequência do fóton emitido?
Estratégia
Se assumirmos que o próton confinado no núcleo pode ser modelado como uma partícula quântica em uma caixa, tudo o que precisamos fazer é usar a Equação\ ref {7.41} para encontrar suas energias\(E_1\)\(E_2\) e. A massa de um próton é\(m = 1.76 \times 10^{-27}kg\). O fóton emitido carrega a diferença de energia\(\Delta E = E_2 - E_1\). Podemos usar a relação\(E_f = hf\) para encontrar sua frequência f.
Solução
O estado fundamental:
\[\begin{align*} E_1 &= \dfrac{\pi^2 \hbar^2}{2mL^2} \\[5pt] &= \dfrac{\pi^2 (1.05 \times 10^{-34} J \cdot s)}{2(1.67 \times 10^{-27} kg)(1.00 \times 10^{-14}m)^2} \\[5pt] &= 3.28 \times 10^{−13}J \\[5pt] &= 2.05 \, MeV \end{align*} \nonumber \]
O primeiro estado de excitação:
\[E_2 = 2^2 E_1 = 4(2.05 \, MeV) = 8.20 \, MeV. \nonumber \]
A energia do fóton emitido é
\[E_f = \Delta E = E_2 - E_1 = 8.20 \, MeV - 2.05 \, MeV = 6.15 \, MeV. \nonumber \]
A frequência do fóton emitido é
\[f = \dfrac{E_f}{h} = \dfrac{6.15 \, MeV}{4.14 \times 10^{-21}MeV \cdot s} = 1.49 \times 10^{21} Hz. \nonumber \]
Significância
Essa é a frequência típica de um raio gama emitido por um núcleo. A energia desse fóton é cerca de 10 milhões de vezes maior do que a de um fóton de luz visível.
O valor esperado da posição de uma partícula em uma caixa é dado por
\[\langle x \rangle = \int_0^L dx \,\psi_n^* (x) x \psi_n(x) = \int_0^L dx\,x|\psi_n^*(x)|^2 = \int_0^L dx\,x \dfrac{2}{L}sin^2 \, \dfrac{nπx}{L} = \dfrac{L}{2}. \label{7.47} \]
Também podemos encontrar o valor esperado do momento ou momento médio de um grande número de partículas em um determinado estado:
\[\begin{align} \langle p \rangle &= \int_0^L dx\psi_n^* (x) \left[-i\hbar \dfrac{d}{dx} \psi_n(x)\right] \label{7.48} \\[5pt] &= -i\hbar \int_0^L dx \sqrt{\dfrac{2}{L}} \, \sin \, \dfrac{n\pi x}{L} \left[ \dfrac{d}{dx} \sqrt{\dfrac{2}{L}} \, \sin \, \dfrac{n\pi x}{L}\right] \\[5pt] &= -i \dfrac{2\hbar}{L} \int_0^L dx \, \sin \, \dfrac{n\pi x}{L} \left[ \dfrac{n\pi}{L} \, \cos \, \dfrac{n\pi x}{L}\right] \\[5pt] &= - i\dfrac{2n\pi \hbar}{L^2} \int_0^L dx \dfrac{1}{2} \sin \, \dfrac{2n\pi x}{L} \\[5pt] &= -i \dfrac{n\pi \hbar}{L^2} \dfrac{L}{2n\pi} \int_0^{2\pi n} d\varphi \, \sin \, \varphi \\[5pt] &= -i \dfrac{\hbar}{2L} \cdot 0 \\[5pt] &= 0. \end{align} \]
Assim, para uma partícula em um estado de energia definida, a posição média está no meio da caixa e o momento médio da partícula é zero, como também seria para uma partícula clássica. Observe que, embora a energia mínima de uma partícula clássica possa ser zero (a partícula pode estar em repouso no meio da caixa), a energia mínima de uma partícula quântica é diferente de zero e dada pela Equação\ ref {7.44}. A energia média das partículas no enésimo estado quântico - seu valor esperado de energia - é
\[E_n = \langle E \rangle = n^2 \dfrac{\pi^2 \hbar^2}{2m}. \label{7.49} \]
O resultado não é surpreendente porque o estado de onda estacionária é um estado de energia definitiva. Qualquer medição de energia desse sistema deve retornar um valor igual a uma dessas energias permitidas.
Nossa análise da partícula quântica em uma caixa não estaria completa sem discutir o princípio de correspondência de Bohr. Esse princípio afirma que, para grandes números quânticos, as leis da física quântica devem fornecer resultados idênticos aos da física clássica. Para ilustrar como esse princípio funciona para uma partícula quântica em uma caixa, traçamos a distribuição de densidade de probabilidade
\[|\psi_n(x)|^2 = \dfrac{2}{L} sin^2 (n\pi x/L) \label{7.50} \]
para encontrar a partícula ao redor da localização\(x\) entre as paredes quando a partícula está no estado quântico\(\psi_n\). \(\PageIndex{3}\)A figura mostra essas distribuições de probabilidade para o estado fundamental, para o primeiro estado excitado e para um estado altamente excitado que corresponde a um grande número quântico. Vemos nesses gráficos que quando uma partícula quântica está no estado fundamental, é mais provável que ela seja encontrada no meio da caixa, onde a distribuição de probabilidade tem o maior valor. Isso não acontece quando a partícula está no primeiro estado excitado, porque agora a distribuição de probabilidade tem o valor zero no meio da caixa, então não há chance de encontrar a partícula lá. Quando uma partícula quântica está no primeiro estado excitado, a distribuição de probabilidade tem dois máximos, e a melhor chance de encontrar a partícula está em posições próximas às localizações desses máximos. Essa imagem quântica é diferente da imagem clássica.
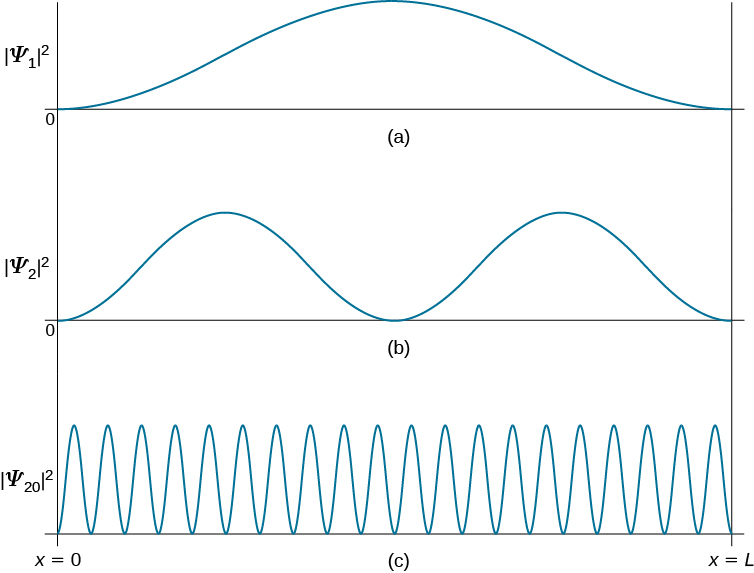
A densidade de probabilidade de encontrar uma partícula clássica entre\(x\) e\(x + \Delta x\) depende de quanto tempo\(Δt\) a partícula passa nessa região. Supondo que sua velocidade u seja constante, esse tempo é\(Δt = Δx/u\), o que também é constante para qualquer local entre as paredes. Portanto, a densidade de probabilidade de encontrar a partícula clássica em\(x\) é uniforme em toda a caixa, e não há um local preferível para encontrar uma partícula clássica. Essa imagem clássica é comparada no limite de grandes números quânticos. Por exemplo, quando uma partícula quântica está em um estado altamente excitado, mostrado na Figura\(\PageIndex{3}\), a densidade de probabilidade é caracterizada por flutuações rápidas e, em seguida, a probabilidade de encontrar a partícula quântica no intervalo Δx não depende de onde esse intervalo está localizado entre as paredes.
Um pequeno carrinho de 0,40 kg está se movendo para frente e para trás ao longo de uma pista de ar entre dois pára-choques localizados a 2,0 m de distância. Não assumimos atrito; as colisões com os para-choques são perfeitamente elásticas, de modo que, entre os para-choques, o carro mantém uma velocidade constante de 0,50 m/s. Tratando o carrinho como uma partícula quântica, estime o valor do número quântico principal que corresponde à sua energia clássica.
Estratégia
Encontramos a energia cinética K do carrinho e sua energia do estado fundamental\(E_1\) como se fosse uma partícula quântica. A energia do carrinho é completamente cinética, então\(K = n^2 E_1\) (Equação\ ref {7.45}). Resolver para n dá\(n = (K/E_1)^{1/2}\).
Solução
A energia cinética do carrinho é
\[K = \dfrac{1}{2} mu^2 = \dfrac{1}{2}(0.40 \, kg)(0.50 \, m/s)^2 = 0.050 \, J. \nonumber \]
O estado fundamental do carrinho, tratado como uma partícula quântica, é
\[E_1 = \dfrac{\pi^2 \hbar^2}{2mL^2} = \dfrac{\pi^2 (1.05 \times 10^{-34} J \cdot s)^2}{2(0.40 \, kg)(2.0 \, m)^2} = 1.700 \times 10^{-68} J. \nonumber \]
Portanto,\[n = (K/E_1)^{1/2} = (0.050/1.700 \times 10^{-68})^{1/2} = 1.2 \times 10^{33}. \nonumber \]
Significância
Vemos neste exemplo que a energia de um sistema clássico é caracterizada por um número quântico muito grande. O princípio da correspondência de Bohr diz respeito a esse tipo de situação. Podemos aplicar o formalismo da mecânica quântica a qualquer tipo de sistema, quântico ou clássico, e os resultados estão corretos em cada caso. No limite dos números quânticos altos, não há vantagem em usar o formalismo quântico porque podemos obter os mesmos resultados com o formalismo menos complicado da mecânica clássica. No entanto, não podemos aplicar o formalismo clássico a um sistema quântico em um estado de energia de baixo número.
(a) Considere um poço quadrado infinito com limites de parede\(x=0\)\(x=L\) e. Qual é a probabilidade de encontrar uma partícula quântica em seu estado fundamental em algum lugar entre\(x=0\) e\(x=L/4\)? (b) Repita a pergunta (a) para uma partícula clássica.
Solução
a. 9,1%; b. 25%
Tendo encontrado os estados estacionários\(ψ_n(x)\) e as energias\(E_n\) resolvendo a equação de SchrDinger independente do tempo (Equação\ ref {7.32}), usamos a Equação 7.4.12 para escrever funções de onda\(Ψ_n(x,t)\) que são soluções da equação de SchrDinger dependente do tempo dada pela Equação 7.4.7. Para uma partícula em uma caixa, isso dá
\[\Psi_n(x,t) = e^{-i\omega_nt} \psi_n(x) = \sqrt{\dfrac{2}{L}}e^{-iE_nt/\hbar}sin \, \dfrac{n\pi x}{L}, \, n = 1,2,3,... \label{7.51} \]
onde as energias são dadas pela Equação\ ref {7.41}.
O modelo de partícula quântica em uma caixa tem aplicações práticas em um campo relativamente novo da optoeletrônica, que lida com dispositivos que convertem sinais elétricos em sinais ópticos. Esse modelo também lida com fenômenos físicos em nanoescala, como uma nanopartícula presa em um baixo potencial elétrico limitado por barreiras de alto potencial.


