7.6: O oscilador harmônico quântico
- Page ID
- 183221
Ao final desta seção, você poderá:
- Descreva o modelo do oscilador harmônico quântico
- Identifique as diferenças entre os modelos clássico e quântico do oscilador harmônico
- Explique situações físicas em que os modelos clássico e quântico coincidem
As oscilações são encontradas em toda a natureza, em coisas como ondas eletromagnéticas, moléculas vibrantes e a suave oscilação de ida e volta de um galho de árvore. Nos capítulos anteriores, usamos a mecânica newtoniana para estudar oscilações macroscópicas, como um bloco em uma mola e um pêndulo simples. Neste capítulo, começamos a estudar sistemas oscilantes usando a mecânica quântica. Começamos com uma revisão do oscilador harmônico clássico.
O oscilador harmônico clássico
Um oscilador harmônico simples é uma partícula ou sistema que sofre movimento harmônico em torno de uma posição de equilíbrio, como um objeto com massa vibrando em uma mola. Nesta seção, consideramos as oscilações somente em uma dimensão. Suponha que uma massa se mova para frente e para trás ao longo da\(x\) direção -em torno da posição de equilíbrio,\(x = 0\). Na mecânica clássica, a partícula se move em resposta a uma força de restauração linear dada por\(F_x = -kx\), onde\(x\) está o deslocamento da partícula de sua posição de equilíbrio. O movimento ocorre entre dois pontos de inflexão\(x \pm A\),, onde A denota a amplitude do movimento. A posição do objeto varia periodicamente no tempo com a frequência angular\(\omega = \sqrt{k/m}\), que depende da massa m do oscilador e da força constante\(k\) da força líquida, e pode ser escrita como
\[x(t) = A \, \cos (\omega t + \phi). \label{7.52} \]
A energia total\(E\) de um oscilador é a soma de sua energia cinética\(K = mu^2/2\) e a energia potencial elástica da força\(U(x) = kx^2/2\),
\[E = \dfrac{1}{2} mu^2 + \dfrac{1}{2}kx^2. \label{7.53} \]
Nos pontos de inflexão\(x = \pm A\), a velocidade do oscilador é zero; portanto, nesses pontos, a energia da oscilação está unicamente na forma de energia potencial\(E = kA^2/2\). O gráfico da energia potencial\(U(x)\) do oscilador versus sua posição\(x\) é uma parábola (Figura\(\PageIndex{1}\)). A função de energia potencial é uma função quadrática de\(x\), medida em relação à posição de equilíbrio. No mesmo gráfico, também representamos graficamente a energia total\(E\) do oscilador, como uma linha horizontal que intercepta a parábola em\(x = \pm A\). Em seguida, a energia cinética\(K\) é representada como a distância vertical entre a linha de energia total e a parábola de energia potencial.
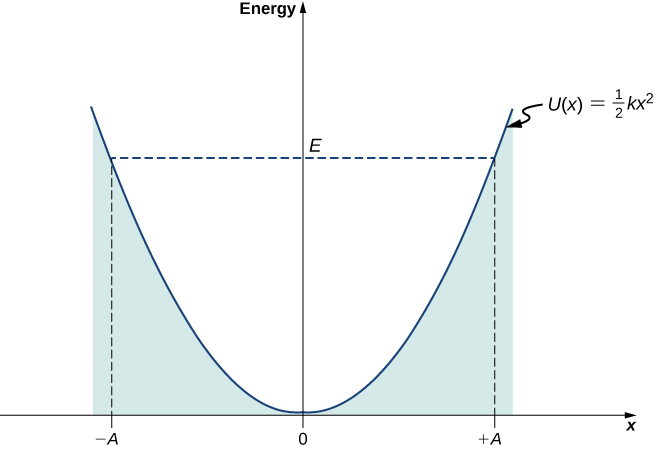
Neste gráfico, o movimento de um oscilador clássico está confinado à região onde sua energia cinética não é negativa, que é o que diz a relação de energia Equation\ ref {7.53}. Fisicamente, isso significa que um oscilador clássico nunca pode ser encontrado além de seus pontos de inflexão, e sua energia depende apenas da distância entre os pontos de inflexão e sua posição de equilíbrio. A energia de um oscilador clássico muda de forma contínua. A menor energia que um oscilador clássico pode ter é zero, o que corresponde a uma situação em que um objeto está em repouso em sua posição de equilíbrio. O estado de energia zero de um oscilador clássico significa simplesmente nenhuma oscilação e nenhum movimento (uma partícula clássica situada na parte inferior do poço potencial na Figura\(\PageIndex{1}\)). Quando um objeto oscila, não importa quão grande ou pequena seja sua energia, ele passa mais tempo perto dos pontos de inflexão, porque é aqui que ele diminui a velocidade e inverte sua direção de movimento. Portanto, a probabilidade de encontrar um oscilador clássico entre os pontos de inflexão é maior perto dos pontos de inflexão e menor na posição de equilíbrio. (Note que isso não é uma declaração de preferência do objeto em reduzir a energia. É uma declaração sobre a rapidez com que o objeto se move por várias regiões.)
O oscilador harmônico quântico
Um problema com essa formulação clássica é que ela não é geral. Não podemos usá-lo, por exemplo, para descrever vibrações de moléculas diatômicas, onde os efeitos quânticos são importantes. O primeiro passo em direção a uma formulação quântica é usar a expressão clássica\(k = m\omega^2\) para limitar a menção de uma constante de “primavera” entre os átomos. Dessa forma, a função de energia potencial pode ser escrita de uma forma mais geral,
\[U(x) = \dfrac{1}{2}m \omega^2 x^2. \label{7.54} \]
A combinação dessa expressão com a equação de Schrdinger independente do tempo fornece
\[-\dfrac{\hbar}{2m} \dfrac{d^2 \psi(x)}{dx^2} + \dfrac{1}{2}m\omega^2 x^2 \psi(x) = E\psi (x). \label{7.55} \]
Para resolver a Equação\ ref {7.55}, ou seja, para encontrar as energias permitidas\(E\) e suas funções de onda\(\psi (x) \) correspondentes, exigimos que as funções de onda sejam simétricas\(x = 0\) (sobre a parte inferior do poço potencial) e sejam normalizáveis. Essas condições garantem que a densidade de probabilidade\(|\psi (x)|^2\) seja finita quando integrada em toda a faixa de x\(-\infty\) de\(+\infty\) a. Como resolver a equação\ ref {7.55} é o assunto de um curso mais avançado em mecânica quântica; aqui, simplesmente citamos os resultados. As energias permitidas são
\[ \begin{align} E_n &= \left(n + \dfrac{1}{2}\right) \hbar \omega \\[5pt] &= \dfrac{2n + 1}{2} \hbar \omega \label{7.56} \end{align} \]
com\(n = 0,1,2,3,...\)
As funções de onda que correspondem a essas energias (os estados estacionários ou estados de energia definida) são
\[\psi_n (x) = N_n e^{-\beta^2 x^2/2} H_n (\beta x), \, n = 0,1,2,3, ... \label{7.57} \]
onde\(\beta = \sqrt{m\omega/\hbar}\),\(N_n\) é a constante de normalização e\(H_n(y)\) é um polinômio de grau\(n\) chamado polinômio de Hermite. Os primeiros quatro polinômios de Hermite são
- \(H_0 (y) = 1\)
- \(H_1 (y) = 2y\)
- \(H_2 (y) = 4y^2 - 2\)
- \(H_3 (y) = 8y^3 - 12 y.\)
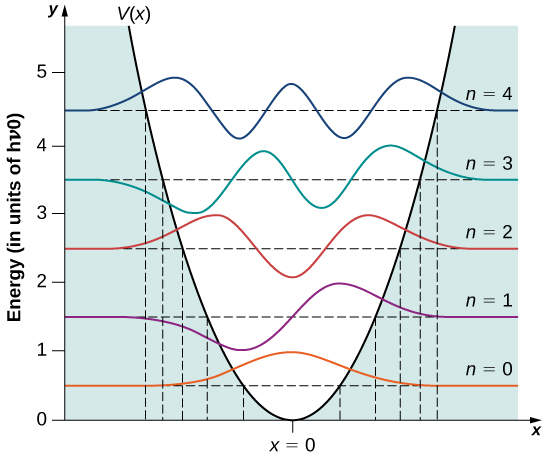
Alguns exemplos de funções de onda são fornecidos na Figura\(\PageIndex{2}\). À medida que o valor do número principal aumenta, as soluções alternam entre funções pares e funções ímpares\(x = 0\).
Encontre a amplitude\(A\) das oscilações de um oscilador clássico com energia igual à energia de um oscilador quântico no estado quântico\(n\).
Estratégia
Para determinar a amplitude\(A\), definimos a energia clássica\(E = kx^2/2 = m\omega^2 \, A^2/2\) igual à\(E_n\) dada pela Equação\ ref {7.56}.
Solução
Nós obtemos
\[\begin{align} E_n &= m\omega^2 A_n^2/2 \nonumber \\[5pt] A_n &= \sqrt{\dfrac{2}{m\omega^2}E_n} \nonumber \\[5pt] &= \sqrt{\dfrac{2}{m\omega^2} \dfrac{2n + 1}{2}\hbar \omega} \nonumber \\[5pt] &= \sqrt{(2n + 1) \dfrac{\hbar}{m\omega}}. \nonumber \end{align} \nonumber \]
Significância
À medida que o número quântico n aumenta, a energia do oscilador e, portanto, a amplitude da oscilação aumentam (para uma frequência angular natural fixa). Para n grande, a amplitude é aproximadamente proporcional à raiz quadrada do número quântico.
Vários recursos interessantes aparecem nesta solução. Ao contrário de um oscilador clássico, as energias medidas de um oscilador quântico podem ter apenas valores de energia dados pela Equação\ ref {7.56}. Além disso, ao contrário do caso de uma partícula quântica em uma caixa, os níveis de energia permitidos são espaçados uniformemente,
\[\begin{align} \Delta E &= E_{n+1} - E_n \\[5pt] &= \dfrac{2(n + 1) + 1}{2} \hbar \omega - \dfrac{2n + 1}{2} \hbar \omega \\[5pt] &= \hbar \omega = hf. \label{7.58} \end{align} \]
Quando uma partícula ligada a esse sistema faz uma transição de um estado de energia mais alta para um estado de energia mais baixa, o quantum de menor energia transportado pelo fóton emitido é necessariamente\(hf\). Da mesma forma, quando a partícula faz uma transição de um estado de baixa energia para um estado de energia mais alta, o quantum de menor energia que pode ser absorvido pela partícula é\(hf\). Um oscilador quântico pode absorver ou emitir energia somente em múltiplos desse quantum de menor energia. Isso é consistente com a hipótese de Planck para as trocas de energia entre a radiação e as paredes da cavidade no problema de radiação do corpo negro.
A molécula\(\ce{HCl}\) diatômica consiste em um átomo de cloro e um átomo de hidrogênio. Como o átomo de cloro é 35 vezes mais massivo que o átomo de hidrogênio, as vibrações da\(\ce{HCl}\) molécula podem ser bem aproximadas assumindo que o átomo de Cl está imóvel e o átomo de H realiza oscilações harmônicas devido a uma força molecular elástica modelada pela lei de Hooke. O espectro vibracional infravermelho medido para cloreto de hidrogênio tem a linha de frequência mais baixa centrada em\(f = 8.88 \times 10^{13} Hz\). Qual é o espaçamento entre as energias vibracionais dessa molécula? Qual é a constante de força k da ligação atômica na molécula de HCl?
Estratégia
A linha de frequência mais baixa corresponde à emissão de fótons de frequência mais baixa. Esses fótons são emitidos quando a molécula faz uma transição entre dois níveis de energia vibracional adjacentes. Supondo que os níveis de energia estejam igualmente espaçados, usamos a Equação\ ref {7.58} para estimar o espaçamento. A molécula é bem aproximada ao tratar o átomo de Cl como sendo infinitamente pesado e o átomo de H como a massa\(m\) que realiza as oscilações. Tratando esse sistema molecular como um oscilador clássico, a constante de força é encontrada a partir da relação clássica\(k = m\omega^2\).
Solução
O espaçamento de energia é
\[ \begin{align} \Delta E &= hf \nonumber \\[5pt] &= (4.14 \times 10^{-15} eV \cdot s)(8.88 \times 10^{13} Hz) \nonumber\\[5pt] &= 0.368 \, eV. \nonumber \end{align} \nonumber \]
A força constante é
\[ \begin{align} k &= m \omega^2 \nonumber \\[5pt] &= m (2\pi f)^2 \nonumber \\[5pt] &= (1.67 \times 10^{ −27} kg)(2\pi \times 8.88 \times 10 ^{13}Hz)^2 \nonumber \\[5pt] &= 520 \, N/m. \nonumber \end{align} \nonumber \]
Significância
A força entre átomos em uma molécula de HCl é surpreendentemente forte. A energia típica liberada nas transições de energia entre os níveis vibracionais está na faixa do infravermelho. Como veremos mais adiante, as transições entre os níveis de energia vibracional de uma molécula diatômica geralmente acompanham as transições entre os níveis de energia rotacional.
A frequência vibracional da molécula diatômica HI de iodeto de hidrogênio é\(6.69×10^{ 13}\,Hz\).
- Qual é a constante de força da ligação molecular entre os átomos de hidrogênio e iodo?
- Qual é a energia do fóton emitido quando essa molécula faz uma transição entre os níveis de energia vibracional adjacentes?
- Responda a um
-
295 N/m
- Resposta b
-
0,277 eV
O oscilador quântico difere do oscilador clássico de três maneiras:
- Primeiro, o estado fundamental de um oscilador quântico não é\(E_0 = \hbar \omega /2\) zero. Na visão clássica, a energia mais baixa é zero. A inexistência de um estado de energia zero é comum a todos os sistemas de mecânica quântica devido às flutuações onipresentes que são uma consequência do princípio da incerteza de Heisenberg. Se uma partícula quântica ficasse imóvel na parte inferior do poço potencial, seu momento e sua posição teriam que ser simultaneamente exatos, o que violaria o princípio da incerteza de Heisenberg. Portanto, o estado de menor energia deve ser caracterizado por incertezas no momento e na posição, portanto, o estado fundamental de uma partícula quântica deve estar acima do fundo do poço potencial.
- Segundo, uma partícula em um potencial de oscilador harmônico quântico pode ser encontrada com probabilidade diferente de zero fora do intervalo\(-A \leq x \leq +A\). Em uma formulação clássica do problema, a partícula não teria energia para estar nessa região. A probabilidade de encontrar uma partícula quântica fundamental na região classicamente proibida é de cerca de 16%.
- Terceiro, as distribuições de densidade de probabilidade\(|\psi_n(x)|^2\) para um oscilador quântico no estado de baixa energia do solo\(\psi_0(x)\),, são maiores no meio do poço\((x = 0)\). Para que a partícula seja encontrada com maior probabilidade no centro do poço, esperamos que a partícula passe a maior parte do tempo lá enquanto oscila. Isso é oposto ao comportamento de um oscilador clássico, no qual a partícula passa a maior parte do tempo se movendo com velocidades relativamente pequenas próximas aos pontos de inflexão.
Encontre o valor esperado da posição de uma partícula no estado fundamental de um oscilador harmônico usando simetria.
- Resposta b
-
\[\langle x \rangle = 0 \nonumber \]
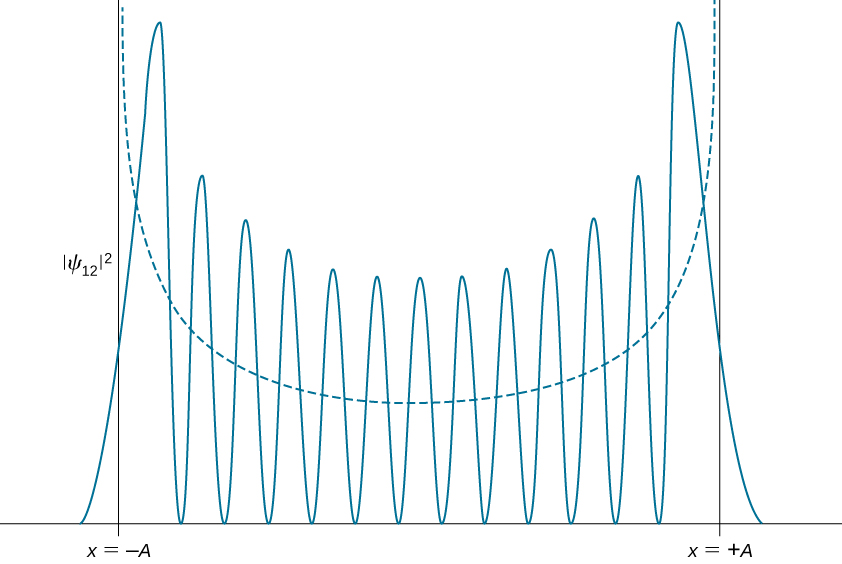
As distribuições de densidade de probabilidade quântica mudam de caráter para estados excitados, tornando-se mais parecidas com a distribuição clássica quando o número quântico aumenta. Já observamos essa mudança para o primeiro estado excitado de um oscilador quântico porque a distribuição atinge o\(|\psi_1(x)|^ 2\) pico em torno dos pontos de inflexão e desaparece na posição de equilíbrio, como visto na Figura\(\PageIndex{2}\). De acordo com o princípio de correspondência de Bohr, no limite dos números quânticos altos, a descrição quântica de um oscilador harmônico converge para a descrição clássica, ilustrada na Figura\(\PageIndex{3}\). A distribuição clássica de densidade de probabilidade correspondente à energia quântica do\(n = 12\) estado é uma aproximação razoavelmente boa da distribuição de probabilidade quântica para um oscilador quântico nesse estado excitado. Esse acordo se torna cada vez melhor para estados altamente empolgados.