7.3: O Princípio da Incerteza de Heisenberg
- Page ID
- 183237
Ao final desta seção, você poderá:
- Descreva o significado físico da relação de incerteza posição-momento
- Explicar as origens do princípio da incerteza na teoria quântica
- Descreva o significado físico da relação de incerteza energia-tempo
O princípio da incerteza de Heisenberg é um princípio fundamental na mecânica quântica. De forma muito aproximada, afirma que, se sabemos tudo sobre onde uma partícula está localizada (a incerteza da posição é pequena), não sabemos nada sobre seu momento (a incerteza do momento é grande) e vice-versa. Versões do princípio da incerteza também existem para outras quantidades, como energia e tempo. Discutimos os princípios de posição dinâmica e incerteza de tempo de energia separadamente.
Momento e posição
Para ilustrar o princípio da incerteza da posição de momento, considere uma partícula livre que se move ao longo da direção x. A partícula se move com velocidade\(u\) e momento constantes\(p = mu\). De acordo com as relações de De Broglie,\(p = \hbar k\)\(E = \hbar \omega\) e. Conforme discutido na seção anterior, a função de onda para uma partícula livre é dada por
\[ \begin{align*} \psi_k(x,t) &= A[\cos \, (\omega t - kx) - i \, \sin \, (\omega t - kx)] \\[4pt] &= A \, e^{-i(\omega t - kx)} \\[4pt] &= A \, e^{-i(\omega t - kx)} \\[4pt] &=A\, e^{-i\omega t} e^{ikx} \end{align*} \nonumber \]
e a densidade da probabilidade\(|\psi_k (x,t)|^2 = A^2\) é uniforme e independente do tempo. A partícula tem a mesma probabilidade de ser encontrada em qualquer lugar ao longo do eixo x, mas tem valores definidos de comprimento de onda e número de onda e, portanto, momento. A incerteza da posição é infinita (estamos completamente incertos sobre a posição) e a incerteza do momento é zero (temos certeza absoluta sobre o momento). Esse relato de uma partícula livre é consistente com o princípio da incerteza de Heisenberg.
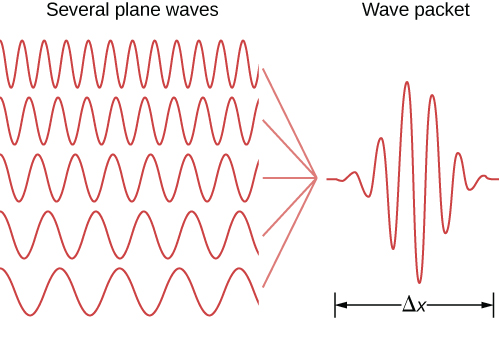
Declarações similares podem ser feitas de partículas localizadas. Na teoria quântica, uma partícula localizada é modelada por uma superposição linear de estados de partículas livres (ou ondas planas) chamada pacote de ondas. Um exemplo de pacote de ondas é mostrado na Figura\(\PageIndex{1}\). Um pacote de ondas contém muitos comprimentos de onda e, portanto, pelas relações de Broglie, muitos momentos — possíveis na mecânica quântica! Essa partícula também tem muitos valores de posição, embora a partícula esteja confinada principalmente ao intervalo\(\Delta x\). A partícula pode ser melhor localizada (\(\Delta x\)pode ser diminuída) se mais estados de ondas planas de diferentes comprimentos de onda ou momentos forem somados da maneira correta (\(\Delta p\)aumentada). De acordo com Heisenberg, essas incertezas obedecem à seguinte relação.
O produto da incerteza na posição de uma partícula e da incerteza em seu momento nunca pode ser inferior à metade da constante de Planck reduzida:
\[\Delta x \Delta p \geq \dfrac{\hbar}{2}. \label{Heisen} \]
Essa relação expressa o princípio da incerteza de Heisenberg. Ele impõe limites ao que podemos saber sobre uma partícula a partir de medições simultâneas de posição e momento. \(\Delta x\)É grande,\(\Delta p\) é pequeno e vice-versa. A equação\ ref {Heisen} pode ser derivada em um curso mais avançado de física moderna. Refletindo sobre essa relação em sua obra Os Princípios Físicos da Teoria Quântica, Heisenberg escreveu: “Qualquer uso das palavras 'posição' e 'velocidade' com precisão superior à dada pela [relação] é tão sem sentido quanto o uso de palavras cujo sentido não está definido”.
Observe que o princípio da incerteza não tem nada a ver com a precisão de um aparato experimental. Mesmo para dispositivos de medição perfeitos, essas incertezas permaneceriam porque se originam na natureza ondulatória da matéria. O valor preciso do produto\(\Delta x \Delta p\) depende da forma específica da função de onda. Curiosamente, a função gaussiana (ou distribuição da curva de sino) fornece o valor mínimo do produto da incerteza:
\[\Delta x \Delta p = \dfrac{\hbar}{2} \nonumber \]
Determine as incertezas mínimas nas posições dos seguintes objetos se suas velocidades forem conhecidas com uma precisão de\(1.0 \times 10^{-3} m/s\):
- um elétron e
- uma bola de boliche de massa de 6,0 kg.
Estratégia
Dada a incerteza na velocidade\(\Delta u = 1.0 \times 10^{-3} m/s\), temos que primeiro determinar a incerteza no momento\(\Delta p = m\Delta u\) e depois inverter a Equação\ ref {Heisen} para encontrar a incerteza na posição
\[\Delta x = \dfrac{\hbar}{2\Delta p}. \nonumber \]
Solução
- Para o elétron:\[\begin{align*} \Delta p &= m\Delta u \\[4pt] &= (9.1 \times 10^{-31} kg)(1.0 \times 10^{-3}m/s) \\[4pt] &= 9.1 \times 10^{-34} kg \cdot m/s,\end{align*} \nonumber \]\[\begin{align*} \Delta x &= \frac{\hbar}{2\Delta p} \\[4pt] &= 5.8 \, cm. \end{align*} \nonumber \]
- Para a bola de boliche:\[\begin{align*} \Delta p &= m\Delta u \\[4pt] &= (6.0 \, kg)(1.0 \times 10^{-3}m/s) \\[4pt] &= 6.0 \times 10^{-3} kg \cdot m/s, \end{align*} \nonumber \]\[\begin{align*} \Delta x &= \frac{\hbar}{2\Delta p} \\[4pt] &= 8.8 \times 10^{-33}m. \end{align*} \nonumber \]
Significância
Ao contrário da incerteza de posição do elétron, a incerteza da posição da bola de boliche é incomensuravelmente pequena. A constante de Planck é muito pequena, então as limitações impostas pelo princípio da incerteza não são perceptíveis em sistemas macroscópicos, como uma bola de boliche.
Estime a energia do estado fundamental de um átomo de hidrogênio usando o princípio da incerteza de Heisenberg. (Dica: De acordo com experimentos anteriores, o tamanho de um átomo de hidrogênio é de aproximadamente 0,1 nm.)
Estratégia
Um elétron ligado a um átomo de hidrogênio pode ser modelado por uma partícula ligada a uma caixa unidimensional de comprimento\(L = 0.1 \, nm\). A função de onda do estado fundamental deste sistema é meia onda. Esse é o maior comprimento de onda que pode “caber” na caixa, então a função de onda corresponde ao estado de menor energia. Observe que essa função tem um formato muito semelhante a uma função gaussiana (curva de sino). Podemos considerar a energia média de uma partícula descrita por essa função (E) como uma boa estimativa da energia do estado fundamental (\(E_0\)). Essa energia média de uma partícula está relacionada à sua média do momento quadrado, que está relacionada à sua incerteza de momento.
Solução
Para resolver esse problema, devemos ser específicos sobre o que se entende por “incerteza de posição” e “incerteza de momentum”. Identificamos a incerteza da posição (Δx) com o desvio padrão da posição (\(σ_x\)) e a incerteza do momento (\(Δp\)) com o desvio padrão do momento (\(σ_p\)). Para a função gaussiana, o produto da incerteza é
\[\sigma_x\sigma_p = \frac{\hbar}{2}, \nonumber \]
onde
\[\sigma_x^2 = x^2 - \overline{x}^2 \nonumber \]
e
\[\sigma_p^2 = p^2 - \overline{p}^2.\nonumber \]
É tão provável que a partícula esteja se movendo para a esquerda quanto para a direita, então\(\overline{p}^2 = 0\). Além disso, a incerteza da posição é comparável ao tamanho da caixa, portanto\(\sigma_x = L\). A energia estimada do estado fundamental é, portanto,
\[\begin{align*} E_0 &= E_{Gaussian} \\[4pt] &= \dfrac{\overline{p}^2}{m} \\[4pt] &= \frac{\sigma_p^2}{2m} \\[4pt] &= \frac{1}{2m} \left(\frac{\hbar}{2\sigma_x}\right)^2 \\[4pt] &= \frac{1}{2m} \left(\frac{\hbar}{2L}\right)^2 \\[4pt] &= \frac{\hbar^2}{8mL^2}. \end{align*} \nonumber \]
\[\begin{align*}E_0 &= \dfrac{(\hbar c)^2}{8(mc^2)L^2} \\[4pt] &= \frac{(197.3 \, eV \cdot nm)^2}{8(0.511 \cdot 10^6 eV)(0.1 \, nm)^2} \\[4pt] &= 0.952 \, eV \approx 1 \, eV. \end{align*} \nonumber \]
Multiplicação do numerador e do denominador por\(c^2\) dados
Significância
Com base em estimativas iniciais do tamanho de um átomo de hidrogênio e no princípio da incerteza, a energia do estado fundamental de um átomo de hidrogênio está na faixa de eV. A energia de ionização de um elétron na energia do estado fundamental é de aproximadamente 10 eV, então essa previsão é aproximadamente confirmada. (Nota: O produto cc geralmente é um valor útil na realização de cálculos em mecânica quântica.)
Energia e tempo
Outro tipo de princípio de incerteza diz respeito às incertezas nas medições simultâneas da energia de um estado quântico e sua vida útil,
\[\Delta E \Delta t \geq \frac{\hbar}{2} \label{H2} \]
onde\(\Delta E\) está a incerteza na medição de energia e\(\Delta t\) é a incerteza na medição da vida útil. O princípio da incerteza energia-tempo não resulta de uma relação do tipo expressa pela Equação\ ref {Heisen} por razões técnicas além desta discussão. No entanto, o significado geral do princípio do tempo de energia é que um estado quântico que existe por pouco tempo não pode ter uma energia definida. O motivo é que a frequência de um estado é inversamente proporcional ao tempo e a frequência se conecta com a energia do estado; portanto, para medir a energia com boa precisão, o estado deve ser observado por muitos ciclos.
Para ilustrar, considere os estados de excitação de um átomo. A vida útil finita desses estados pode ser deduzida das formas das linhas espectrais observadas nos espectros de emissão atômica. Cada vez que um estado excitado decai, a energia emitida é ligeiramente diferente e, portanto, a linha de emissão é caracterizada por uma distribuição das frequências espectrais (ou comprimentos de onda) dos fótons emitidos. Como resultado, todas as linhas espectrais são caracterizadas por larguras espectrais. A energia média do fóton emitido corresponde à energia teórica do estado excitado e fornece a localização espectral do pico da linha de emissão. Estados de vida curta têm larguras espectrais amplas e estados de vida longa têm larguras espectrais estreitas.
Um átomo normalmente existe em um estado excitado por cerca de\(\Delta t = 10^{-8} s\). Estime a incerteza\(\Delta f\) na frequência dos fótons emitidos quando um átomo faz uma transição de um estado excitado com a emissão simultânea de um fóton com uma frequência média de\(f = 7.1 \times 10^{14} Hz\). A radiação emitida é monocromática?
Estratégia
Invertemos a Equação\ ref {H2} para obter a incerteza energética\(\Delta E \approx \hbar /2\Delta t\) e a combinamos com a energia do fóton\(E = hf\) a ser obtida\(\Delta f\). Para estimar se a emissão é monocromática ou não, avaliamos\(\Delta f/f\).
Solução
A propagação nas energias dos fótons é\(\Delta E = h \Delta f\). Portanto,
\[\Delta E \approx \frac{\hbar}{2 \Delta t} \Rightarrow h \Delta t \approx \frac{\hbar}{2 \Delta t} \Rightarrow \Delta f \approx \frac{1}{4\pi \Delta t} = \frac{1}{4\pi (10^{-8}s)} = 8.0 \times 10^6 \, Hz, \nonumber \]
\[\frac{\Delta f}{f} = \frac{8.0 \times 10^6 \, Hz}{7.1 \times 10^{14} \, Hz} = 1.1 \times 10^{-8}. \nonumber \]
Significância
Como os fótons emitidos têm suas frequências dentro de uma\(1.1 \times 10^{-6}\) porcentagem da frequência média, a radiação emitida pode ser considerada monocromática.
Um átomo de sódio faz uma transição do primeiro estado excitado para o estado fundamental, emitindo um fóton de 589,0 nm com energia de 2,105 eV. Se a vida útil desse estado de excitação é\(1.6 \times 10^{-8} s\), qual é a incerteza na energia desse estado excitado? Qual é a largura da linha espectral correspondente?
- Responda
-
\(4.1 \times 10^{-8} eV\);\(1.1 \times 10^{-5} nm\)


