7.2: Funções de onda

Objetivos de

Ao final desta seção, você poderá:

• Descreva a interpretação estatística da função de onda
• Use a função de onda para determinar probabilidades
• Calcule os valores esperados de posição, momento e energia cinética

No capítulo anterior, vimos que as partículas agem em alguns casos como partículas e em outros casos como ondas. Mas o que significa para uma partícula “agir como uma onda”? O que exatamente é “acenar”? Quais regras governam como essa onda muda e se propaga? Como a função de onda é usada para fazer previsões? Por exemplo, se a amplitude de uma onda de elétrons é dada por uma função de posição e tempo,\(\Psi \, (x,t)\), definida para todo x, onde exatamente está o elétron? O objetivo deste capítulo é responder a essas perguntas.

Usando a função Wave

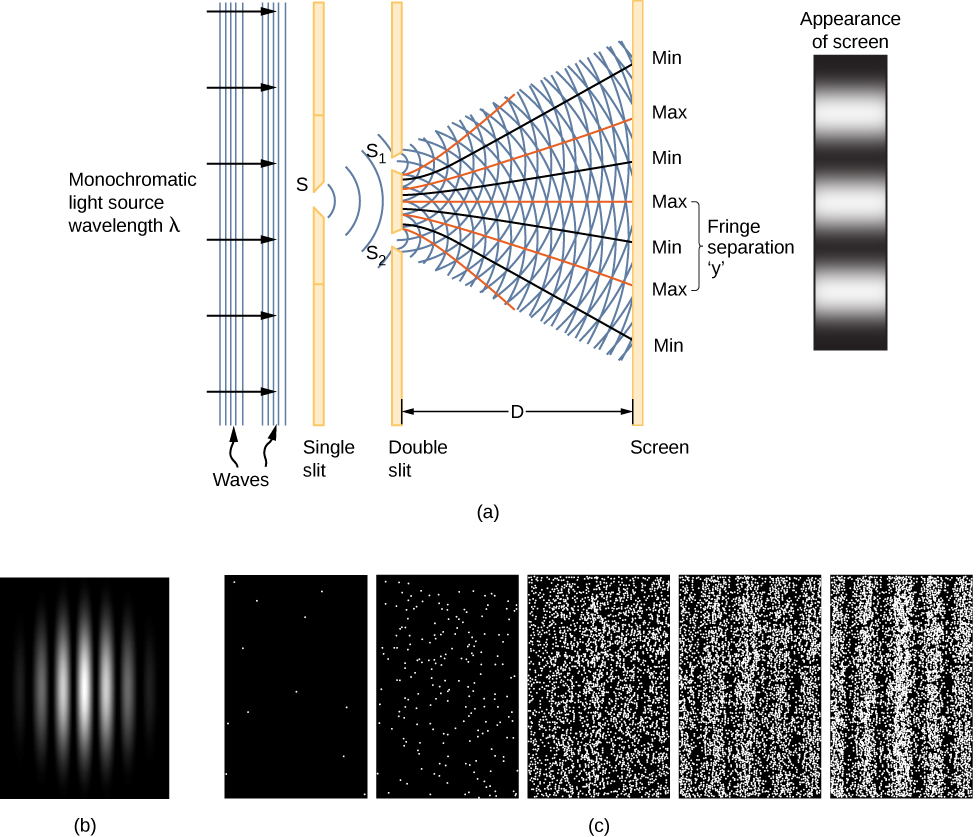
Uma pista sobre o significado físico da função de onda\(\Psi \, (x,t)\) é fornecida pela interferência de duas fendas da luz monocromática (Figura\(\PageIndex{1}\)) que se comporta como ondas eletromagnéticas. A função de onda de uma onda de luz é dada por E (x, t), e sua densidade de energia é dada por\(|E|^2\), onde E é a intensidade do campo elétrico. A energia de um fóton individual depende apenas da frequência da luz\(\epsilon_{photon} = hf\), portanto,\(|E|^2\) é proporcional ao número de fótons. Quando as ondas de luz\(S_1\) interferem com as ondas de\(S_2\) luz da tela de visualização (a uma distância D), um padrão de interferência é produzido (\(\PageIndex{1a}\)). As franjas brilhantes correspondem aos pontos de interferência construtiva das ondas de luz, e as franjas escuras correspondem aos pontos de interferência destrutiva das ondas de luz (\(\PageIndex{1b}\)).

Suponha que a tela inicialmente não esteja exposta à luz. Se a tela for exposta a uma luz muito fraca, o padrão de interferência aparecerá gradualmente (Figura\(\PageIndex{1c}\), da esquerda para a direita). Os golpes individuais de fótons na tela aparecem como pontos. Espera-se que a densidade de pontos seja grande em locais onde o padrão de interferência será, em última análise, o mais intenso. Em outras palavras, a probabilidade (por unidade de área) de que um único fóton atinja um determinado ponto na tela é proporcional ao quadrado do campo elétrico total, nesse\(|E|^2\) ponto. Sob as condições certas, o mesmo padrão de interferência se desenvolve para partículas de matéria, como elétrons.

Figura\(\PageIndex{1}\): Interferência de luz monocromática em duas fendas. (a) Esquema de interferência de duas fendas; (b) padrão de interferência de luz; (c) padrão de interferência construído gradualmente sob luz de baixa intensidade (da esquerda para a direita).

Nota

Visite esta simulação interativa para saber mais sobre a interferência de ondas quânticas.

O quadrado da onda de matéria\(|\Psi|^2\) em uma dimensão tem uma interpretação semelhante ao quadrado do campo elétrico\(|E|^2\). Ele fornece a probabilidade de que uma partícula seja encontrada em uma determinada posição e tempo por unidade de comprimento, também chamada de densidade de probabilidade. A probabilidade (\(P\)) de uma partícula ser encontrada em um intervalo estreito (x, x + dx) no tempo t é, portanto,

\[P(x,x + dx) = |\Psi \, (x,t)|^2 dx. \label{7.1} \]

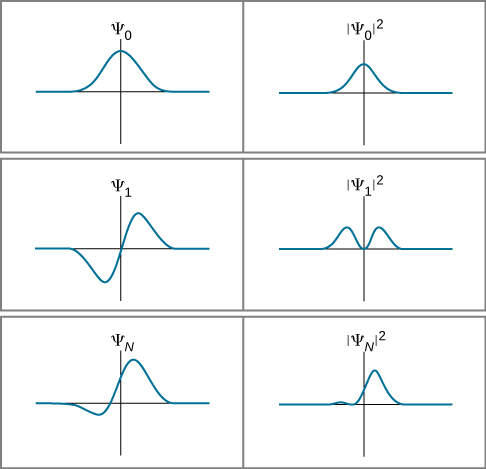
(Posteriormente, definimos a magnitude quadrada para o caso geral de uma função com “partes imaginárias”.) Essa interpretação probabilística da função de onda é chamada de interpretação de Born. Exemplos de funções de onda e seus quadrados para um determinado tempo\(t\) são fornecidos na Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Vários exemplos de funções de onda e o quadrado correspondente de suas funções de onda.

Se a função de onda variar lentamente ao longo do intervalo\(\Delta x\), a probabilidade de uma partícula ser encontrada no intervalo é de aproximadamente

\[P(x,x + \Delta x) \approx |\Psi \, (x,t)|^2 \delta x. \label{7.2} \]

Observe que a quadratura da função de onda garante que a probabilidade seja positiva. (Isso é semelhante ao quadrado da intensidade do campo elétrico — que pode ser positiva ou negativa — para obter um valor positivo de intensidade.) No entanto, se a função de onda não variar lentamente, devemos integrar:

\[P(x,x + \Delta x) = \int_x^{x + \Delta x} |\Psi \, (x,t)|^2 dx. \label{7.3} \]

Essa probabilidade é apenas a área sob a função\(|Ψ(x,t)|^2\) entre\(x\)\(x+Δx\) e. A probabilidade de encontrar a partícula “em algum lugar” (a condição de normalização) é

\[P(-\infty, +\infty) = \int_{-\infty}^{\infty} |\Psi \, (x,t)|^2 dx = 1.\label{7.4} \]

Para uma partícula em duas dimensões, a integração é sobre uma área e requer uma integral dupla; para uma partícula em três dimensões, a integração é maior que um volume e requer uma integral tripla. Por enquanto, nos limitamos ao caso unidimensional simples.

Exemplo\(\PageIndex{1A}\): Where Is the Ball? (Part I)

Uma bola é obrigada a se mover ao longo de uma linha dentro de um tubo de comprimento\(L\). É igualmente provável que a bola seja encontrada em qualquer lugar do tubo em algum momento\(t\). Qual é a probabilidade de encontrar a bola na metade esquerda do tubo naquele momento? (A resposta é 50%, é claro, mas como obtemos essa resposta usando a interpretação probabilística da função de onda da mecânica quântica?)

Estratégia

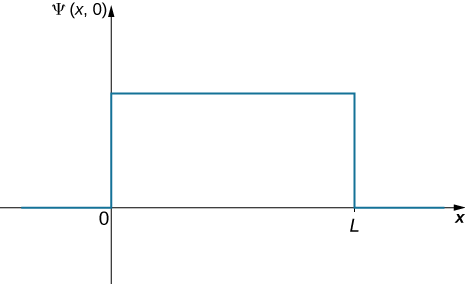
O primeiro passo é anotar a função de onda. A bola é igualmente parecida com a de ser encontrada em qualquer lugar da caixa, então uma maneira de descrevê-la com uma função de onda constante (Figura\(\PageIndex{3}\)). A condição de normalização pode ser usada para encontrar o valor da função e uma integração simples na metade da caixa produz a resposta final.

Figura\(\PageIndex{3}\): Wavefunction for a ball in a tube of length L.

Solution

The wavefunction of the ball can be written as \(\Psi \, (x,t) = C(0 < x < L)\), where \(C\) is a constant, and \(\Psi \, (x,t) = 0\) otherwise. We can determine the constant C by applying the normalization condition (we set \(t = 0\) to simplify the notation):

\[P(\infty, +\infty) = \int_{-\infty}^{\infty} |C|^2 dx = 1. \nonumber \]

This integral can be broken into three parts: (1) negative infinity to zero, (2) zero to L, and (3) L to infinity. The particle is constrained to be in the tube, so \(C=0\) outside the tube and the first and last integrations are zero. The above equation can therefore be written

\[P(x = 0, L) = \int_0^L |C|^2 dx = 1. \nonumber \]

The value C does not depend on x and can be taken out of the integral, so we obtain

\[|C|^2 \int_0^L dx = 1. \nonumber \]

Integration gives

\[C = \sqrt{\dfrac{1}{L}}. \nonumber \]

To determine the probability of finding the ball in the first half of the box (\(0 < x < L\)), we have

\[\begin{align} P(x = 0, L/2) &= \int_0^{L/2} \left|\sqrt{\dfrac{1}{L}}\right|^2dx \nonumber \\[5pt] &= \left(\dfrac{1}{L}\right)\dfrac{L}{2} \nonumber \\[5pt] &= 0.50. \end{align} \nonumber \]

Significance

The probability of finding the ball in the first half of the tube is 50%, as expected. Two observations are noteworthy. First, this result corresponds to the area under the constant function from \(x=0\) to \(L/2\) (the area of a square left of L/2). Second, this calculation requires an integration of the square of the wavefunction. A common mistake in performing such calculations is to forget to square the wavefunction before integration.

Example \(\PageIndex{1B}\): Where Is the Ball? (Part II)

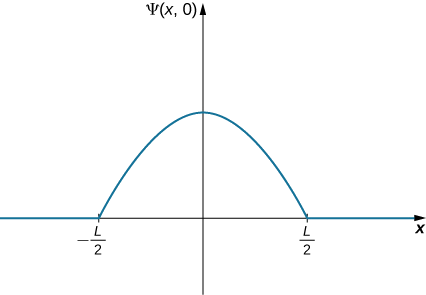
A ball is again constrained to move along a line inside a tube of length L. This time, the ball is found preferentially in the middle of the tube. One way to represent its wavefunction is with a simple cosine function (Figure \(\PageIndex{4}\)). What is the probability of finding the ball in the last one-quarter of the tube?

Figura\(\PageIndex{4}\): Função de onda para uma bola em um tubo de comprimento L, onde a bola está preferencialmente no meio do tubo.

Estratégia

Usamos a mesma estratégia de antes. Nesse caso, a função de onda tem duas constantes desconhecidas: uma está associada ao comprimento de onda da onda e a outra é a amplitude da onda. Determinamos a amplitude usando as condições de contorno do problema e avaliamos o comprimento de onda usando a condição de normalização. A integração do quadrado da função de onda no último quarto do tubo produz a resposta final. O cálculo é simplificado centralizando nosso sistema de coordenadas no pico da função de onda.

Solução

A função de onda da bola pode ser escrita

\[\Psi \, (x,t) = A \, \cos \, (kx) (-L/2 < x < L/2), \nonumber \]

onde\(A\) está a amplitude da função de onda e\(k = 2\pi/\lambda\) é seu número de onda. Além desse intervalo, a amplitude da função de onda é zero porque a bola está confinada ao tubo. Exigir que a função de onda termine na extremidade direita do tubo dá

\[\Psi \left(x = \dfrac{L}{2}, 0 \right) = 0. \nonumber \]

Avaliando a função de onda em\(x = L/2\) dá

\[A \, \cos \, (kL/2) = 0. \nonumber \]

Essa equação é satisfeita se o argumento do cosseno for um múltiplo integral de\(π/2\),\(3π/2\)\(5π/2\), e assim por diante. Nesse caso, temos

\[\dfrac{kL}{2} = \dfrac{\pi}{2}, \nonumber \]ou\[k = \dfrac{\pi}{L}. \nonumber \]

A aplicação da condição de normalização dá\(A = \sqrt{2/L}\), portanto, a função de onda da bola é

\[\Psi \, (x,0) = \sqrt{\dfrac{2}{L}} \, cos \, (\pi x/L), \, -L/2 < x < L/2. \nonumber \]

Para determinar a probabilidade de encontrar a bola no último quarto do tubo, quadramos a função e integramos:

\[P(x = L/4, L/2) = \int_{L/4}^{L/2} \left|\sqrt{\dfrac{2}{L}} \, \cos \, \left(\dfrac{\pi x}{L}\right) \right| ^2 dx = 0.091. \nonumber \]

Significância

A probabilidade de encontrar a bola no último quarto do tubo é de 9,1%. A bola tem um comprimento de onda definido (\(\lambda = 2L\)). Se o tubo tiver um comprimento macroscópico (\(L = 1 \, m\)), o momento da bola é

\[p = \dfrac{h}{\lambda} = \dfrac{h}{2L} \approx10^{-36} m/s. \nonumber \]

Esse momento é muito pequeno para ser medido por qualquer instrumento humano.

Uma interpretação da função de onda

Agora estamos em posição de começar a responder às perguntas feitas no início desta seção. Primeiro, para uma partícula viajante descrita por\(\Psi \, (x,t) = A \, \sin \, (kx - \omega t)\), o que é “ondulação”? Com base na discussão acima, a resposta é uma função matemática que pode, entre outras coisas, ser usada para determinar onde a partícula provavelmente estará quando uma medição de posição for realizada. Em segundo lugar, como a função de onda é usada para fazer previsões? Se for necessário encontrar a probabilidade de uma partícula ser encontrada em um determinado intervalo, eleve ao quadrado a função de onda e integre-a ao longo do intervalo de interesse. Em breve, você aprenderá que a função de onda também pode ser usada para fazer muitos outros tipos de previsões.

Terceiro, se uma onda de matéria é dada pela função de onda\(\Psi \, (x,t)\), onde exatamente está a partícula? Existem duas respostas: (1) quando o observador não está olhando (ou a partícula não está sendo detectada de outra forma), a partícula está em todo lugar (\(x = -\infty, +\infty\)); e (2) quando o observador está olhando (a partícula está sendo detectada), a partícula “salta para” um estado de posição específico (\(x,x + dx\) ) com uma probabilidade dada por

\[P(x,x + dx) = |\Psi \, (x,t)|^2 dx \nonumber \]

por meio de um processo chamado redução de estado ou colapso da função de onda. Essa resposta é chamada de interpretação de Copenhague da função de onda ou da mecânica quântica.

Para ilustrar essa interpretação, considere o caso simples de uma partícula que pode ocupar um pequeno recipiente em\(x_1\) ou\(x_2\) (Figura\(\PageIndex{5}\)). Na física clássica, assumimos que a partícula está localizada em\(x_1\) ou\(x_2\) quando o observador não está olhando. No entanto, na mecânica quântica, a partícula pode existir em um estado de posição indefinida, ou seja, ela pode estar localizada em\(x_1\) e\(x_2\) quando o observador não está olhando. A suposição de que uma partícula só pode ter um valor de posição (quando o observador não está olhando) é abandonada. Comentários semelhantes podem ser feitos sobre outras quantidades mensuráveis, como momentum e energia.

Figura\(\PageIndex{5}\): A two-state system of position of a particle.

The bizarre consequences of the Copenhagen interpretation of quantum mechanics are illustrated by a creative thought experiment first articulated by Erwin Schrödinger (National Geographic, 2013) (\(\PageIndex{6}\)):

“A cat is placed in a steel box along with a Geiger counter, a vial of poison, a hammer, and a radioactive substance. When the radioactive substance decays, the Geiger detects it and triggers the hammer to release the poison, which subsequently kills the cat. The radioactive decay is a random [probabilistic] process, and there is no way to predict when it will happen. Physicists say the atom exists in a state known as a superposition—both decayed and not decayed at the same time. Until the box is opened, an observer doesn’t know whether the cat is alive or dead—because the cat’s fate is intrinsically tied to whether or not the atom has decayed and the cat would [according to the Copenhagen interpretation] be “living and dead ... in equal parts” until it is observed.”

Figure \(\PageIndex{6}\): Schrödinger’s cat.

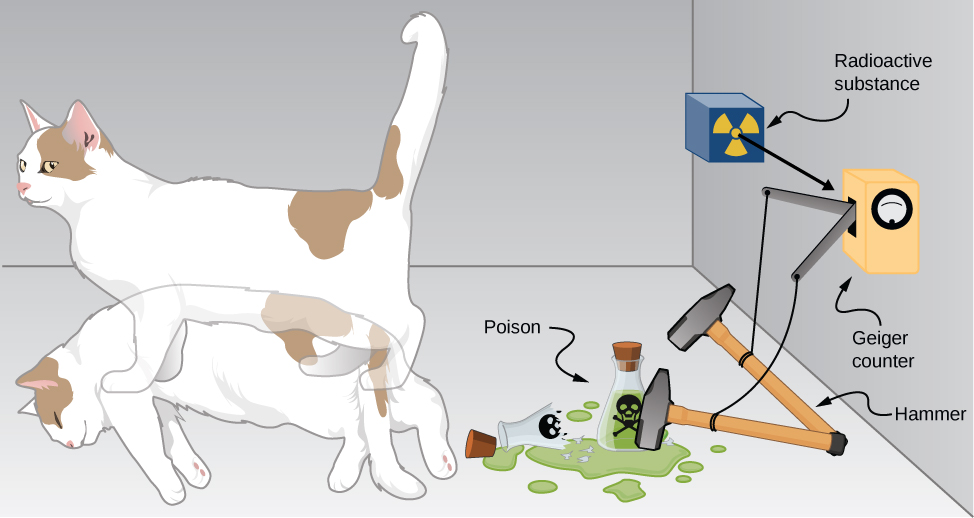
Schrödinger took the absurd implications of this thought experiment (a cat simultaneously dead and alive) as an argument against the Copenhagen interpretation. However, this interpretation remains the most commonly taught view of quantum mechanics.

Quantum Computing: qubits

Two-state systems (left and right, atom decays and does not decay, and so on) are often used to illustrate the principles of quantum mechanics. These systems find many applications in nature, including electron spin and mixed states of particles, atoms, and even molecules. Two-state systems are also finding application in the quantum computer, as mentioned in the introduction of this chapter. Unlike a digital computer, which encodes information in binary digits (zeroes and ones), a quantum computer stores and manipulates data in the form of quantum bits, or qubits. In general, a qubit is not in a state of zero or one, but rather in a mixed state of zero and one. If a large number of qubits are placed in the same quantum state, the measurement of an individual qubit would produce a zero with a probability p, and a one with a probability \(q = 1 - p\). Some scientists believe that quantum computers are the future of the computer industry.

Complex Conjugates

Later in this section, you will see how to use the wavefunction to describe particles that are “free” or bound by forces to other particles. The specific form of the wavefunction depends on the details of the physical system. A peculiarity of quantum theory is that these functions are usually complex functions. A complex function is one that contains one or more imaginary numbers (\(i = \sqrt{-1}\)). Experimental measurements produce real (nonimaginary) numbers only, so the above procedure to use the wavefunction must be slightly modified. In general, the probability that a particle is found in the narrow interval \((x, x + dx)\) at time \(t\) is given by

\[P (x,x + dx) = |\Psi \, (x,t)|^2 dx = \Psi^* (x,t) \, \Psi \, (x,t) \, dx, \label{7.5} \]

where \(\Psi^* (x,t)\) is the complex conjugate of the wavefunction. The complex conjugate of a function is obtaining by replacing every occurrence of \(i = \sqrt{-1}\) in that function with \(-i\). This procedure eliminates complex numbers in all predictions because the product \(\Psi^* (x,t) \, \Psi \, (x,t)\) is always a real number.

Exercise \(\PageIndex{1}\)

If \(a = 3 + 4i\), what is the product \(a^*a\)?

Answer

\[(3 + 4i)(3 - 4i) = 9 - 16i^2 = 25 \nonumber \]

Consider the motion of a free particle that moves along the x-direction. As the name suggests, a free particle experiences no forces and so moves with a constant velocity. As we will see in a later section of this chapter, a formal quantum mechanical treatment of a free particle indicates that its wavefunction has real and complex parts. In particular, the wavefunction is given by

\[\Psi \, (x,t) = A \, \cos \, (kx - \omega t) + i A \, \sin \, (kx - \omega t), \label{eq56} \]

where \(A\) is the amplitude, \(k\) is the wave number, and \(ω\) is the angular frequency. Euler’s formula

\[\underbrace{e^{i\phi} = \cos \, (\phi) + i \, \sin \, (\phi)}_{\text{Euler’s formula}} \nonumber \]

can be used to rewrite Equation \ref{eq56} in the form

\[\Psi \, (x,t) = Ae^{i(kx - \omega t)} = Ae^{i\phi}, \nonumber \]

where \(\phi\) is the phase angle. If the wavefunction varies slowly over the interval \(\Delta x\), the probability of finding the particle in that interval is

\[P (x,x + \Delta x) \approx \Psi^* (x,t) \, \Psi \, (x,t) \, \Delta x = (Ae^{i\phi})(A^* e^{-i\phi}) \, \Delta x = (A^*A) \Delta x. \nonumber \]

If \(A\) has real and complex parts (\(a+ib\), where \(a\) and \(b\) are real constants), then

\[A^*A = (a + ib)(a - ib) = a^2 + b^2. \nonumber \]

Notice that the complex numbers have vanished. Thus,

\[P(x,x + \Delta x) \approx |A|^2 \delta x \nonumber \]

is a real quantity. The interpretation of \(\Psi^* (x,t) \, \Psi \, (x,t)\) as a probability density ensures that the predictions of quantum mechanics can be checked in the “real world.”

Exercise \(\PageIndex{2}\)

Suppose that a particle with energy E is moving along the x-axis and is confined in the region between 0 and L. One possible wavefunction is

\[\psi (x,t) =\begin{cases}
Ae^{-iEt/\hbar} \sin \, \dfrac{\pi x}{L} & 0 \leq x \leq L \\
0 & x < 0 \text{ and } x > L \end{cases} \nonumber \]

Determine the normalization constant.

Answer

\(A = \sqrt{2/L}\)

Expectation Values

In classical mechanics, the solution to an equation of motion is a function of a measurable quantity, such as \(x(t)\), where \(x\) is the position and \(t\) is the time. Note that the particle has one value of position for any time \(t\). In quantum mechanics, however, the solution to an equation of motion is a wavefunction, \(\Psi \, (x,t)\). The particle has many values of position for any time \(t\), and only the probability density of finding the particle, \(|\Psi \, (x,t)|^2\), can be known. The average value of position for a large number of particles with the same wavefunction is expected to be

\[\langle x \rangle = \int_{-\infty}^{\infty} xP(x,t) \, dx = \int_{-\infty}^{\infty} x \Psi^* (x,t) \, \Psi \, (x,t) \, dx. \label{7.6} \]

This is called the expectation value of the position. It is usually written

\[\langle x \rangle = \int_{-\infty}^{\infty} \Psi^* (x,t) \, x \Psi \, (x,t) \, dx. \label{7.7} \]

where the \(x\) is sandwiched between the wavefunctions. The reason for this will become apparent soon. Formally, \(x\) is called the position operator.

At this point, it is important to stress that a wavefunction can be written in terms of other quantities as well, such as velocity (\(v\)), momentum (\(p\)), and kinetic energy (\(K\)). The expectation value of momentum, for example, can be written

\[\langle p \rangle = \int_{-\infty}^{\infty} \Psi^* (p,t) \, p\Psi \, (p,t) \, dp, \label{7.8} \]

where \(dp\) is used instead of \(dx\) to indicate an infinitesimal interval in momentum. In some cases, we know the wavefunction in position, \(\Psi \, (x,t)\), but seek the expectation of momentum. The procedure for doing this is

\[\langle p \rangle = \int_{-\infty}^{\infty} \Psi^* (x,t) \, \left(-i\hbar \dfrac{d}{dx}\right) \, \Psi \, (x,t) \, dx, \label{7.9} \]

where the quantity in parentheses, sandwiched between the wavefunctions, is called the momentum operator in the x-direction. [The momentum operator in Equation \ref{7.9} is said to be the position-space representation of the momentum operator.] The momentum operator must act (operate) on the wavefunction to the right, and then the result must be multiplied by the complex conjugate of the wavefunction on the left, before integration. The momentum operator in the x-direction is sometimes denoted

\[\langle p \rangle = - i\hbar \dfrac{d}{dx},\label{7.10} \]

Momentum operators for the y- and z-directions are defined similarly. This operator and many others are derived in a more advanced course in modern physics. In some cases, this derivation is relatively simple. For example, the kinetic energy operator is just

\[\begin{align} (K)_{op} &= \dfrac{1}{2}m(v_x)_{op}^2 \\[5pt] &= \dfrac{(p_x)^2_{op}}{2m} \\[5pt] &= \dfrac {\left(-i\hbar \dfrac{d}{dx}\right)^2}{2m} \\[5pt] &= \dfrac{-\hbar^2}{2m} \left(\dfrac{d}{dx}\right)\left(\dfrac{d}{dx}\right).\label{7.11} \end{align} \]

Thus, if we seek an expectation value of kinetic energy of a particle in one dimension, two successive ordinary derivatives of the wavefunction are required before integration.

Symmetry can simplify calculations

Expectation-value calculations are often simplified by exploiting the symmetry of wavefunctions. Symmetric wavefunctions can be even or odd. An even function is a function that satisfies

\[\psi(x) = \psi(-x). \label{7.12} \]

In contrast, an odd function is a function that satisfies

\[\psi(x) = -\psi(-x).\label{7.13} \]

An example of even and odd functions is shown in Figure \(\PageIndex{7}\). An even function is symmetric about the y-axis. This function is produced by reflecting \(\psi (x)\) for \(x > 0\) about the vertical y-axis. By comparison, an odd function is generated by reflecting the function about the y-axis and then about the x-axis. (An odd function is also referred to as an anti-symmetric function.)

Figura\(\PageIndex{7}\): Exemplos de funções de ondas pares e ímpares.

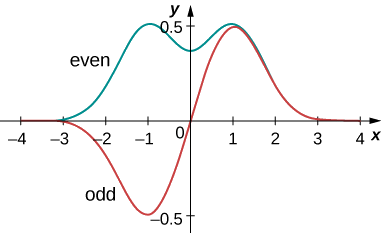
Em geral, uma função par multiplicada por uma função par produz uma função par. Um exemplo simples de uma função uniforme é o produto\(x^2e^{-x^2}\) (até vezes até é par). Da mesma forma, uma função ímpar vezes uma função ímpar produz uma função par, como x sin x (ímpar vezes ímpar é par). No entanto, uma função ímpar multiplicada por uma função par produz uma função ímpar, como\(x^2e^{-x^2}\) (vezes ímpar par é ímpar). A integral sobre todo o espaço de uma função ímpar é zero, porque a área total da função acima do eixo x cancela a área (negativa) abaixo dela. Como mostra o próximo exemplo, essa propriedade de funções ímpares é muito útil.

Exemplo\(\PageIndex{2A}\): Expectation Value (Part I)

A função de onda normalizada de uma partícula é

\[\psi(x) = e^{-|x|/x_0} /\sqrt{x_0}. \nonumber \]

Encontre o valor esperado da posição.

Estratégia

Substitua a função de onda na Equação\ ref {7.7} e avalie. O operador de posição introduz somente um fator multiplicativo, portanto, o operador de posição não precisa ser “imprensado”.

Solução

Primeiro multiplique e depois integre:

\[\begin{align*} \langle x \rangle &= \int_{-\infty}^{\infty} dx\,x|\psi(x)|^2 \nonumber \\[4pt] &= \int_{-\infty}^{\infty} dx\, x|\dfrac{e^{-|x|/x_0}}{\sqrt{x_0}}|^2 \nonumber \\[4pt] &= \dfrac{1}{x_0} \int_{-\infty}^{\infty} dx\, xe^{-2|x|/x_0} \nonumber \\[4pt] &= 0. \nonumber \end{align*} \nonumber \]

Significância

A função no integrando (\(xe^{-2|x|/x_0}\)) é ímpar, pois é o produto de uma função ímpar (x) e uma função par (\(e^{-2|x|/x_0}\)). A integral desaparece porque a área total da função em torno do eixo x cancela a área (negativa) abaixo dela. O resultado (\(\langle x \rangle = 0\)) não é surpreendente, pois a função de densidade de probabilidade é simétrica aproximadamente\(x = 0\).

Exemplo\(\PageIndex{2B}\): Expectation Value (Part II)

A função de onda dependente do tempo de uma partícula confinada a uma região entre 0 e L é

\[\psi(x,t) = A \, e^{-i\omega t} \sin \, (\pi x/L) \nonumber \]

onde\(\omega\) é a frequência angular e\(E\) é a energia da partícula. (Nota: A função varia como um seno devido aos limites (0 a L). Quando\(x = 0\), o fator seno é zero e a função de onda é zero, consistente com as condições de contorno.) Calcule os valores esperados de posição, momento e energia cinética.

Estratégia

Devemos primeiro normalizar a função de onda para encontrar A. Em seguida, usamos os operadores para calcular os valores esperados.

Solução

Cálculo da constante de normalização:

\[\begin{align*} 1 &= \int_0^L dx\, \psi^* (x) \psi(x) \nonumber \\[4pt] &= \int_0^L dx \, \left(A e^{+i\omega t} \sin \, \dfrac{\pi x}{L}\right) \left(A e^{-i\omega t} \sin \, \dfrac{\pi x}{L}\right) \nonumber \\[4pt] &= A^2 \int_0^L dx \, \sin^2 \, \dfrac{\pi x}{L} \nonumber \\[4pt] &= A^2 \dfrac{L}{2} \nonumber \\[4pt] \Rightarrow A &= \sqrt{\dfrac{2}{L}}. \nonumber \end{align*} \nonumber \]

O valor esperado da posição é

\[\begin{align*}\langle x \rangle &= \int_0^L dx \, \psi^* (x) x \psi(x) \nonumber \\[4pt] &= \int_0^L dx \, \left(A e^{+i\omega t} \sin \, \dfrac{\pi x}{L}\right) x \left(A e^{-i\omega t} \sin \, \dfrac{\pi x}{L}\right) \nonumber \\[4pt] &= A^2 \int_0^L dx\,x \, \sin^2 \, \dfrac{\pi x}{L} \nonumber \\[4pt] &= A^2 \dfrac{L^2}{4} \nonumber \\[4pt] \Rightarrow A &= \dfrac{L}{2}. \nonumber \end{align*} \nonumber \]

O valor esperado do momento na direção x também requer uma integral. Para configurar essa integral, o operador associado deve, por regra, agir à direita na função de onda\(\psi(x)\):

\[\begin{align*} -i\hbar\dfrac{d}{dx} \psi(x) &= -i\hbar \dfrac{d}{dx} Ae^{-i\omega t}\sin \, \dfrac{\pi x}{L} \nonumber \\[4pt] &= - i\dfrac{Ah}{2L} e^{-i\omega t} \cos\, \dfrac{\pi x}{L}. \nonumber \end{align*} \nonumber \]

Portanto, o valor esperado do momentum é

\[ \begin{align*} \langle p \rangle &= \int_0^L dx \left(Ae^{+i\omega t}sin \dfrac{\pi x}{L}\right)\left(-i \dfrac{Ah}{2L} e^{-i\omega t} cos \, \dfrac{\pi x}{L}\right) \nonumber \\[4pt] &= -i \dfrac{A^2h}{4L} \int_0^L dx \, \sin \, \dfrac{2\pi x}{L} \nonumber \\[4pt] &= 0. \nonumber \end{align*} \nonumber \]

A função na integral é uma função senoidal com um comprimento de onda igual à largura do poço, L —uma função ímpar sobre\(x = L/2\). Como resultado, a integral desaparece.

O valor esperado da energia cinética na direção x exige que o operador associado atue na função de onda:

\[ \begin{align} -\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2} \psi (x) &= - \dfrac{\hbar^2}{2m} \dfrac{d^2}{dx^2} Ae^{-i\omega t} \, \sin \, \dfrac{\pi x}{L} \nonumber \\[4pt] &= - \dfrac{\hbar^2}{2m} Ae^{-i\omega t} \dfrac{d^2}{dx^2} \, \sin \, \dfrac{\pi x}{L} \nonumber \\[4pt] &= \dfrac{Ah^2}{8mL^2} e^{-i\omega t} \, \sin \, \dfrac{\pi x}{L}. \nonumber \end{align} \nonumber \]

Assim, o valor esperado da energia cinética é

\[\begin{align*} \langle K \rangle &= \int_0^L dx \left( Ae^{+i\omega t} \, \sin \, \dfrac{\pi x}{L}\right) \left(\dfrac{Ah^2}{8mL^2} e^{-i\omega t} \, \sin \, \dfrac{\pi x}{L}\right) \nonumber \\[4pt] &= \dfrac{A^2h^2}{8mL^2} \int_0^L dx \, \sin^2 \, \dfrac{\pi x}{L} \nonumber \\[4pt] &= \dfrac{A^2h^2}{8mL^2} \dfrac{L}{2} \nonumber \\[4pt] &= \dfrac{h^2}{8mL^2}. \end{align*} \nonumber \]

Significância

A posição média de um grande número de partículas nesse estado é\(L/2\). O momento médio dessas partículas é zero porque uma determinada partícula tem a mesma probabilidade de se mover para a direita ou para a esquerda. No entanto, a partícula não está em repouso porque sua energia cinética média não é zero. Finalmente, a densidade de probabilidade é

\[|\psi|^2 = (2/L) \, \sin^2 (\pi x/L). \nonumber \]

Essa densidade de probabilidade é maior no local\(L/2\) e é zero em\(x = 0\) e em\(x = L\). Observe que essas conclusões não dependem explicitamente do tempo.

Exercício\(\PageIndex{3}\)

Para a partícula no exemplo acima, determine a probabilidade de localizá-la entre as posições\(0\)\(L/4\) e.

Resposta

\((1/2 - 1/\pi) /2 = 9\%\)

A mecânica quântica faz muitas previsões surpreendentes. No entanto, em 1920, Niels Bohr (fundador do Instituto Niels Bohr em Copenhague, do qual obtemos o termo “interpretação de Copenhague”) afirmou que as previsões da mecânica quântica e da mecânica clássica devem concordar com todos os sistemas macroscópicos, como planetas em órbita, bolas saltitantes, cadeiras de balanço e molas. Esse princípio de correspondência agora é geralmente aceito. Isso sugere que as regras da mecânica clássica são uma aproximação das regras da mecânica quântica para sistemas com energias muito grandes. A mecânica quântica descreve tanto o mundo microscópico quanto o macroscópico, mas a mecânica clássica descreve apenas o último.