12.5: Teorema binomial
- Page ID
- 183093
Ao final desta seção, você poderá:
- Use o Triângulo de Pascal para expandir um binômio
- Avalie um coeficiente binomial
- Use o Teorema Binomial para expandir um binômio
Antes de começar, faça este teste de prontidão.
- Simplifique:\(\frac{7 \cdot 6 \cdot 5 \cdot 4}{4 \cdot 3 \cdot 2 \cdot 1}\).
Se você perdeu esse problema, revise o Exemplo 1.25. - Expandir:\((3 x+5)^{2}\).
Se você perdeu esse problema, consulte o Exemplo 5.32. - Expandir:\((x-y)^{2}\).
Se você perdeu esse problema, consulte o Exemplo 5.32.
Use o triângulo de Pascal para expandir um binômio
Em nosso trabalho anterior, temos binômios quadrados usando FOIL ou usando o Padrão de Quadrados Binomiais. Também podemos dizer que expandimos\((a+b)^{2}\).
\((a+b)^{2}=a^{2}+2 a b+b^{2}\)
Para expandir\((a+b)^{3}\), reconhecemos que isso é\((a+b)^{2}(a+b)\) e multiplicamos.
\((a+b)^{3}\)
\((a+b)^{2}(a+b)\)
\(\left(a^{2}+2 a b+b^{2}\right)(a+b)\)
\(a^{3}+2 a^{2} b+a b^{2}+a^{2} b+2 a b^{2}+b^{3}\)
\(a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)
\((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)
Para encontrar um método que seja menos tedioso e que funcione para expansões mais altas\((a+b)^{7}\), como, novamente, procuramos padrões em algumas expansões.
| Número de termos | Primeiro mandato | Último mandato | |
|---|---|---|---|
| \((a+b)^{1}=a+b\) | \(2\) | \(a^{1}\) | \(b^{1}\) |
| \((a+b)^{2}=a^{2}+2 a b+b^{2}\) | \(3\) | \(a^{2}\) | \(b^{2}\) |
| \((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\) | \(4\) | \(a^{3}\) | \(b^{3}\) |
| \((a+b)^{4}=a^{4}+4 a^{3} b+6 a^{2} b^{2}+4 a b^{3}+b^{4}\) | \(5\) | \(a^{4}\) | \(b^{4}\) |
| \((a+b)^{5}=a^{5}+5 a^{4} b+10 a^{3} b^{2}+10 a^{2} b^{3}+5 a b^{4}+b^{5}\) | \(6\) | \(a^{5}\) | \(b^{5}\) |
| \((a+b)^{n}\) | \(n\) | \(a^{n}\) | \(b^{n}\) |
Observe que o primeiro e o último termos mostram apenas uma variável. Lembre-se disso\(a^{0}=1\), para que possamos reescrever o primeiro e o último termos para incluir as duas variáveis. Por exemplo, poderíamos expandir\((a+b)^{3}\) para mostrar cada termo com as duas variáveis.
Geralmente, não mostramos os expoentes zero, assim como costumamos escrever\(x\) em vez de\(1x\).
Padrões na expansão do\((a+b)^{n}\)
- O número de termos é\(n+1\).
- O primeiro termo é\(a^{n}\) e o último termo é\(b^{n}\).
- Os expoentes\(a\) diminuem em um em cada termo, indo da esquerda para a direita.
- Os expoentes\(b\) aumentam em um em cada termo, indo da esquerda para a direita.
- A soma dos expoentes em qualquer termo é\(n\).
Vejamos um exemplo para destacar os últimos três padrões.
A partir dos padrões que identificamos, vemos que as variáveis na expansão de\((a+b)^{n}\), seriam
\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}\).
Para encontrar os coeficientes dos termos, escrevemos nossas expansões novamente com foco nos coeficientes. Nós reescrevemos os coeficientes para a direita formando uma matriz de coeficientes.
A matriz à direita é chamada de Triângulo de Pascal. Observe que cada número na matriz é a soma dos dois números mais próximos na linha acima. Podemos encontrar a próxima linha começando e terminando com um e depois adicionando dois números adjacentes.
Esse triângulo fornece os coeficientes dos termos quando expandimos binômios.
Triângulo de Pascal
No próximo exemplo, usaremos esse triângulo e os padrões que reconhecemos para expandir o binômio.
Use o Triângulo de Pascal para expandir\((x+y)^{6}\).
Solução:
Sabemos que as variáveis dessa expansão seguirão o padrão que identificamos. Os expoentes diferentes de zero\(x\) começarão em seis e diminuirão para um. Os expoentes diferentes de zero\(y\) começarão em um e aumentarão para seis. A soma dos expoentes em cada termo será seis. Em nosso padrão,\(a=x\)\(b=y\) e.
\(\begin{array}{l}{(a+b)^{n}=a^{n}+\_\_\_a^{n-1} b^{1}+\_\_\_a^{n-2} b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}} \\ {(x+y)^{6}=x^{6}+\_\_\_x^{5} y^{1}+\_\_\_x^{4} y^{2}+\_\_\_x^{3} y^{3}+\_\_\_x^{2} y^{4}+\_\_\_x^{1} y^{5}+y^{6}}\end{array}\)
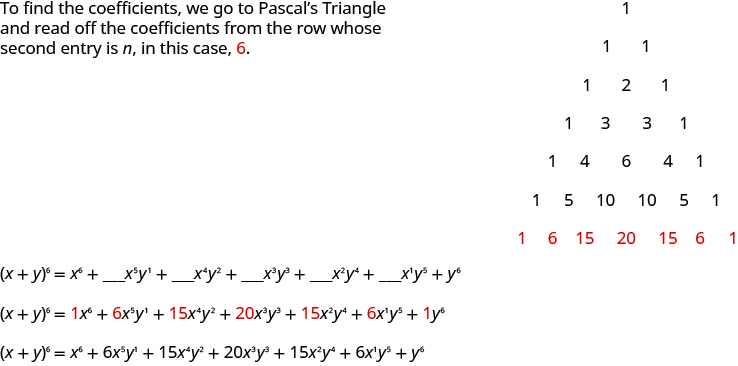
Use o Triângulo de Pascal para expandir\((x+y)^{5}\).
- Responda
-
\(\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}\)
Use o Triângulo de Pascal para expandir\((p+q)^{7}\).
- Responda
-
\(\begin{array}{c}{p^{7}+7 p^{6} q+21 p^{5} q^{2}+35 p^{4} q^{3}} {+35 p^{3} q^{4}+21 p^{2} q^{5}+7 p q^{6}+q^{7}}\end{array}\)
No próximo exemplo, queremos expandir um binômio com uma variável e uma constante. Precisamos identificar\(a\) e\(b\) aplicar cuidadosamente o padrão.
Use o Triângulo de Pascal para expandir\((x+3)^{5}\).
Solução:
Identificamos o\(a\) e\(b\) do padrão.
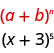
Em nosso padrão,\(a=x\)\(b=3\) e.
Sabemos que as variáveis dessa expansão seguirão o padrão que identificamos. A soma dos expoentes em cada termo será cinco.
\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} \)
\((x+3)^{5}=x^{5}+\_\_\_x^{4}\cdot3^{1}+\_\_\_x^{3}\cdot3^{2}+\_\_\_x^{2}\cdot3^{3}+\_\_\_x^{1}\cdot3^{4}+3^{5}\)

Use o Triângulo de Pascal para expandir\((x+2)^{4}\).
- Responda
-
\(x^{4}+8 x^{3}+24 x^{2}+32 x+16\)
Use o Triângulo de Pascal para expandir\((x+1)^{6}\).
- Responda
-
\(\begin{array}{l}{x^{6}+6 x^{5}+15 x^{4}+20 x^{3}+15 x^{2}} {+6 x+1}\end{array}\)
No próximo exemplo, o binômio é uma diferença e o primeiro termo tem uma constante multiplicada pela variável. Depois de identificarmos o\(a\) e\(b\) do padrão, devemos novamente aplicar o padrão com cuidado.
Use o Triângulo de Pascal para expandir\((3x-2)^{4}\).
Solução:
Identificamos o\(a\) e\(b\) do padrão.
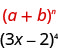
Em nosso padrão,\(a=3x\)\(b=-2\) e.

\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} \)
\((3 x-2 )^{4}=1 \cdot\left(\stackrel{3}{x}+4(3 x)^{3}(-2)^{1}+6(3 x)^{2}(-2)^{2}+4(3 x)^{1}(-2)^{3}+1 \cdot(-2)^{4}\right.\)
\((3 x-2)^{4}=81 x^{4}+4\left(27 x^{3}\right)(-2)+6\left(9 x^{2}\right)(4)+4(3 x)(-8)+1 \cdot 16\)
\((3 x-2 )^{4}=81 x^{4}-216 x^{3}+216 x^{2}-96 x+16\)
Use o Triângulo de Pascal para expandir\((2x-3)^{4}\).
- Responda
-
\(16 x^{4}-96 x^{3}+216 x^{2}-216 x+81\)
Use o Triângulo de Pascal para expandir\((2x-1)^{6}\).
- Responda
-
\(\begin{array}{l}{64 x^{6}-192 x^{5}+240 x^{4}-160 x^{3}} {+60 x^{2}-12 x+1}\end{array}\)
Avalie um coeficiente binomial
Embora o Triângulo de Pascal seja um método para expandir um binômio, também veremos outro método. Antes de chegarmos a isso, precisamos introduzir um pouco mais de notação fatorial. Essa notação não é usada apenas para expandir binômios, mas também no estudo e uso da probabilidade.
Para encontrar os coeficientes dos termos dos binômios expandidos, precisaremos ser capazes de avaliar a notação\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) que é chamada de coeficiente binomial. Lemos\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) como “\(n\)escolha\(r\)” ou “\(n\)tomada\(r\) de cada vez”.
Um coeficiente binomial\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\), onde\(r\) e\(b\) são números inteiros com\(0 \leq r \leq n\), é definido como
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
Lemos\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) como “\(n\)escolher\(r\)” ou “\(n\)\(r\)tirada de cada vez”.
Avalie:
- \(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)
- \(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)
Solução:
a. Usaremos a definição de um coeficiente binomial,
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
\(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
Use a definição\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), onde\(n=5, r=1\).
\(\frac{5 !}{1 !(5-1) !}\)
Simplifique.
\(\frac{5 !}{1 !(4) !}\)
Reescrever\(5!\) como\(5\cdot 4!\)
\(\frac{5 \cdot 4 !}{1 ! \cdot 4 !}\)
Simplifique, removendo fatores comuns.
\(\frac{5\cdot \cancel{4 !}}{1 ! \cdot \cancel{4 !}}\)
Simplifique.
\(5\)
\(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)=5\)
b.\(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)
Use a definição\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), onde\(n=7, r=7\).
\(\frac{7 !}{7 !(7-7) !}\)
Simplifique.
\(\frac{7 !}{7 !(0) !}\)
Simplifique. Lembrar\(0!=1\).
\(1\)
\(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)=1\)
c.\(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)
Use a definição\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), onde\(n=4, r=0\).
\(\frac{4 !}{0 !(4-0) !}\)
Simplifique.
\(\frac{4 !}{0 !(4) !}\)
Simplifique.
\(1\)
\(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)=1\)
d.\(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)
Use a definição\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), onde\(n=8, r=5\).
\(\frac{8 !}{5 !(8-5) !}\)
Simplifique.
\(\frac{8 !}{5 !(3) !}\)
Reescreva\(8!\) como\(8\cdot 7\cdot 6\cdot 5!\) e remova os fatores comuns.
\(\frac{8\cdot7\cdot\cancel{6}\cdot\cancel{5!}}{\cancel{5!}\cdot\cancel{3}\cdot\cancel{2}\cdot1}\)
Simplifique.
\(56\)
\(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)=56\)
Avalie cada coeficiente binomial:
- \(\left( \begin{array}{l}{6} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{8} \\ {8}\end{array}\right)\)
- \(\left( \begin{array}{l}{5} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{7} \\ {3}\end{array}\right)\)
- Responda
-
- \(6\)
- \(1\)
- \(1\)
- \(35\)
Avalie cada coeficiente binomial:
- \(\left( \begin{array}{l}{2} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{11} \\ {11}\end{array}\right)\)
- \(\left( \begin{array}{l}{9} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{6} \\ {5}\end{array}\right)\)
- Responda
-
- \(2\)
- \(1\)
- \(1\)
- \(6\)
No exemplo anterior,,\((a)\)\((b)\),\((c)\) demonstre algumas propriedades especiais dos coeficientes binomiais.
Propriedades dos coeficientes binomiais
\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
Use o teorema binomial para expandir um binômio
Agora estamos prontos para usar o método alternativo de expansão de binômios. O Teorema Binomial usa o mesmo padrão para as variáveis, mas usa o coeficiente binomial para o coeficiente de cada termo.
Teorema binomial
Para qualquer número real\(a\) e\(b\), um inteiro positivo\(n\),
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Use o Teorema Binomial para expandir\((p+q)^{4}\).
Solução:
Identificamos o\(a\) e\(b\) do padrão.
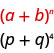
Em nosso padrão,\(a=p\)\(b=q\) e.
Usamos o Teorema Binomial.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Substitua os valores\(a=p, b=q\)\(n=4\) e.
\((p+q)^{4}=\left( \begin{array}{c}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{4-1} q^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{4-2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p^{4-3} q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}\)
Simplifique os expoentes.
\((p+q)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{3} q+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}\)
Avalie os coeficientes, lembre-se,\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
\((p+q)^{4}=1 p^{4}+4 p^{3} q^{1}+\frac{4 !}{2 !(2) !} p^{2} q^{2}+\frac{4 !}{3 !(4-3) !} p^{1} q^{3}+1 q^{4}\)
\((p+q)^{4}=p^{4}+4 p^{3} q+6 p^{2} q^{2}+4 p q^{3}+q^{4}\)
Use o Teorema Binomial para expandir\((x+y)^{5}\).
- Responda
-
\(\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}\)
Use o Teorema Binomial para expandir\((m+n)^{6}\).
- Responda
-
\(\begin{array}{l}{m^{6}+6 m^{5} n+15 m^{4} n^{2}+20 m^{3} n^{3}} {+15 m^{2} n^{4}+6 m n^{5}+n^{6}}\end{array}\)
Observe que quando expandimos\((p+q)^{4}\) no último exemplo, usando o Teorema Binomial, obtivemos os mesmos coeficientes que obteríamos usando o Triângulo de Pascal.
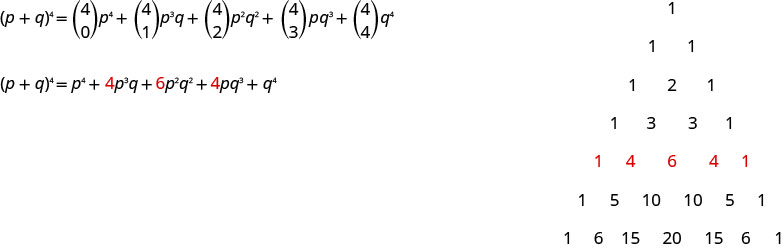
No exemplo a seguir, o binômio é uma diferença. Quando o binômio é uma diferença, devemos ter cuidado ao identificar os valores que usaremos no padrão.
Use o Teorema Binomial para expandir\((x-2)^{5}\).
Solução:
Identificamos o\(a\) e\(b\) do padrão.
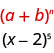
Em nosso padrão,\(a=x\)\(b=-2\) e.
Usamos o Teorema Binomial.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Substitua os valores\(a=x, b=-2\),\(n=5\) e.
\((x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{5-1}(-2)^{1}+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{5-2}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{5-3}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x^{5-4}(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}\)
Simplifique os coeficientes. Lembre-se,\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\).
\((x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{4}(-2)+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{3}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{2}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}\)
\((x-2)^{5}=1 x^{5}+5(-2) x^{4}+\frac{5 !}{2 ! \cdot 3 !}(-2)^{2} x^{3}+\frac{5 !}{3 ! 2 !}(-2)^{3} x^{2}+\frac{5 !}{4 !1 !}(-2)^{4} x+1(-2)^{5}\)
\((x-2)^{5}=x^{5}+5(-2) x^{4}+10 \cdot 4 \cdot x^{3}+10(-8) x^{2}+5 \cdot 16 \cdot x+1(-32)\)
\((x-2)^{5}=x^{5}-10 x^{4}+40 x^{3}-80 x^{2}+80 x-32\)
Use o Teorema Binomial para expandir\((x-3)^{5}\).
- Responda
-
\(\begin{array}{l}{x^{5}-15 x^{4}+90 x^{3}-270 x^{2}} {+405 x-243}\end{array}\)
Use o Teorema Binomial para expandir\((y-1)^{6}\).
- Responda
-
\(\begin{array}{l}{y^{6}-6 y^{5}+15 y^{4}-20 y^{3}+15 y^{2}} {-6 y+1}\end{array}\)
As coisas podem ficar confusas quando os dois termos têm um coeficiente e uma variável.
Use o Teorema Binomial para expandir\((2x-3y)^{4}\).
Solução:
Identificamos o\(a\) e\(b\) do padrão.
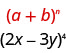
Em nosso padrão,\(a=2x\)\(b=-3y\) e.
Usamos o Teorema Binomial.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Substitua os valores\(a=2x, b=-3y\)\(n=4\) e.
\((2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{4-1}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{4-2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{4-3}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) (-3y)^{4}\)
Simplifique os expoentes.
\((2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{3}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{1}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right)(-3 y)^{4}\)
Avalie os coeficientes. Lembre-se,\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
\((2 x-3 y)^{4}=1(2 x)^{4}+4(2 x)^{3}(-3 y)^{1}+\frac{4 !}{2 !(2 x) !}(2 x)^{2}+\frac{4 !}{3 !(4-3) !}(2 x)^{3}(-3 y)^{3}+1(-3 y)^{4}\)
\((2 x-3 y)^{4}=16 x^{4}+4 \cdot 8 x^{3}(-3 y)+6\left(4 x^{2}\right)\left(9 y^{2}\right)+4(2 x)\left(-27 y^{3}\right)+81 y^{4}\)
\((2 x-3 y)^{4}=16 x^{4}-96 x^{3} y+216 x^{2} y^{2}-216 x y^{3}+81 y^{4}\)
Use o Teorema Binomial para expandir\((3x-2y)^{5}\).
- Responda
-
\(\begin{array}{l}{243 x^{5}-810 x^{4} y+1080 x^{3} y^{2}} {-720 x^{2} y^{3}+240 x y^{4}-32 y^{5}}\end{array}\)
Use o Teorema Binomial para expandir\((4x-3y)^{4}\).
- Responda
-
\(\begin{array}{l}{256 x^{4}-768 x^{3} y+864 x^{2} y^{2}} {-432 x y^{3}+81 y^{4}}\end{array}\)
A verdadeira beleza do Teorema Binomial é que ele fornece uma fórmula para qualquer termo específico da expansão sem precisar calcular a soma total. Vamos procurar um padrão no Teorema Binomial.
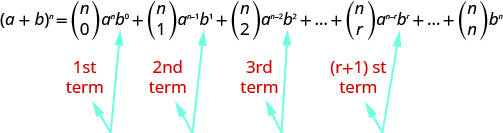
Observe que, em cada caso, o expoente no\(b\) é um a menos que o número do termo. O\((r+1)^{st}\) termo é o termo em que o expoente de\(b\) está\(r\). Assim, podemos usar o formato do\((r+1)^{st}\) termo para encontrar o valor de um termo específico.
Encontre um termo específico em uma expansão binomial
O\((r+1)^{s t}\) termo na expansão de\((a+b)^{n}\) é
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}\)
Encontre o quarto termo de\((x+y)^{7}\).
Solução:
| Em nosso padrão,\(n=7, a=x\)\(b=y\) e. | 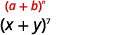 |
|
Estamos procurando o quarto mandato. Desde\(r+1=4\) então\(r=3\). |
|
| Escreva a fórmula | 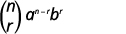 |
| Substitua os valores\(n=7, r=3, a=x\),\(b=y\) e. | 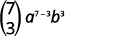 |
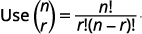 |
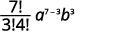 |
| Simplifique. | 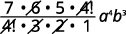 |
| Simplifique. |  |
Encontre o terceiro termo de\((x+y)^{6}\).
- Responda
-
\(15x^{4}y^{2}\)
Encontre o quinto termo de\((a+b)^{8}\).
- Responda
-
\(8ab^{7}\)
Encontre o coeficiente do\(x^{6}\) termo de\((x+3)^{9}\).
Solução:
| Em nosso padrão, então\(n=9, a=x\),\(b=3\) e. |

|
| Estamos procurando o coeficiente do\(x^{6}\) termo. Desde então\(a=x\), e\(x^{9-r}=x^{6}\), nós sabemos\(r=3\). | |
| Escreva a fórmula. |
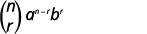
|
| Substitua os valores\(n=9, 4=3, a=x\),\(b=3\) e. |
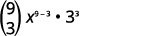
|
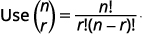
|
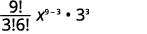
|
| Simplifique. |
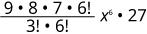
|
| Simplifique. |
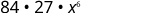
|
| Simplifique. |

|
Encontre o coeficiente do\(x^{5}\) termo de\((x+4)^{8}\).
- Responda
-
\(7,168\)
Encontre o coeficiente do\(x^{4}\) termo de\((x+2)^{7}\).
- Responda
-
\(280\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com sequências.
Conceitos-chave
- Padrões na expansão de\ ((a+b) ^ {n}\ (
- O número de termos é\(n+1\).
- O primeiro termo é\(a^{n}\) e o último termo é\(b^{n}\).
- Os expoentes\(a\) diminuem em um em cada termo, indo da esquerda para a direita.
- Os expoentes\(b\) aumentam em um em cada termo, indo da esquerda para a direita.
- A soma dos expoentes em qualquer termo é\(n\).
- Triângulo de Pascal

- Coeficiente binomial \(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\): Um coeficiente binomial\(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\), onde\(r\) e\(n\) são números inteiros com\(0≤r≤n\), é definido como
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
Lemos\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) como “\(n\)escolha\(r\)” ou “\(n\)tomada\(r\) de cada vez”.
- Propriedades dos coeficientes binomiais
\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
- Teorema binomial:
Para qualquer número\(a\) real\(b\) e número inteiro positivo\(n\),
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)


