12.4: Sequências e séries geométricas
- Page ID
- 183045
Ao final desta seção, você poderá:
- Determine se uma sequência é geométrica
- Encontre o termo geral (\(n\)ésimo termo) de uma sequência geométrica
- Encontre a soma dos primeiros\(n\) termos de uma sequência geométrica
- Encontre a soma de uma série geométrica infinita
- Aplique sequências e séries geométricas no mundo real
Antes de começar, faça este teste de prontidão.
- Simplifique:\(\frac{24}{32}\).
Se você perdeu esse problema, revise o Exemplo 1.24. - Avalie: a.\(3^{4}\)\(\left(\frac{1}{2}\right)^{4}\) b.
Se você perdeu esse problema, revise o Exemplo 1.19. - Se\(f(x)=4 \cdot 3^{x}\), encontre a.\(f(1)\) b.\(f(2)\)\(f(3)\) c.
Se você perdeu esse problema, revise o Exemplo 3.49.
Determine se uma sequência é geométrica
Agora estamos prontos para ver o segundo tipo especial de sequência, a sequência geométrica.
Uma sequência é chamada de sequência geométrica se a razão entre termos consecutivos for sempre a mesma. A razão entre termos consecutivos em uma sequência geométrica é\(r\), a razão comum, onde\(n\) é maior ou igual a dois.
Uma sequência geométrica é uma sequência em que a razão entre termos consecutivos é sempre a mesma.
A razão entre termos consecutivos\(\frac{a_{n}}{a_{n-1}}\),\(r\), é a proporção comum. \(n\)é maior ou igual a dois.
Considere essas sequências.
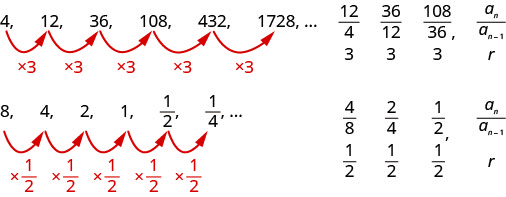
Determine se cada sequência é geométrica. Em caso afirmativo, indique a proporção comum.
- \(4,8,16,32,64,128, \dots\)
- \(-2,6,-12,36,-72,216, \dots\)
- \(27,9,3,1, \frac{1}{3}, \frac{1}{9}, \ldots\)
Solução:
Para determinar se a sequência é geométrica, encontramos a proporção dos termos consecutivos mostrados.
a. Encontre a proporção dos termos consecutivos
\(\begin{aligned} 4, \quad& \:8, \quad 16, \quad 32, \quad 64, \quad 128, \dots \\ &\frac{8}{4} \quad\frac{16}{8}\quad\frac{32}{16}\quad\frac{64}{32}\quad\frac{128}{64} \\ &\:2 \quad\:\:\: 2 \quad\quad2\quad\quad2\quad\quad2 \end{aligned}\)
A sequência é geométrica. A ração comum é\(r=2\).
b. Encontre a proporção dos termos consecutivos
\(\begin{aligned}-\:2,\quad &\:\:\:6,\quad -12,\quad 36,\quad \:-72\quad \:\:216,\dots \\ & \frac{6}{-2}\quad\frac{-12}{6}\quad\frac{36}{-12}\quad\frac{-72}{36}\quad\frac{216}{-72} \\ & -3\quad -2\quad\:\: -3\quad \:\:\:-2\quad \:\:-3 \end{aligned}\)
A sequência não é geométrica. Não há uma proporção comum.
c. Encontre a proporção dos termos consecutivos
\(\begin{aligned}27,\quad &\:\:9,\quad 3,\quad 1,\quad \frac{1}{3},\quad \frac{1}{9}, \ldots\\ & \frac{9}{27}\quad\frac{3}{9}\quad\frac{1}{3}\quad\frac{\frac{1}{3}}{1}\quad\frac{\frac{1}{9}}{\frac{1}{3}}\\ &\frac{1}{3}\quad\;\:\frac{1}{3}\quad\frac{1}{3}\quad\:\frac{1}{3}\quad\:\frac{1}{3}\end{aligned}\)
A sequência é geométrica. A proporção comum é\(r=\frac{1}{3}\).
Determine se cada sequência é geométrica. Em caso afirmativo, indique a proporção comum.
- \(7,21,63,189,567,1,701, \dots\)
- \(64,16,4,1, \frac{1}{4}, \frac{1}{16}, \dots\)
- \(2,4,12,48,240,1,440, \dots\)
- Responda
-
- A sequência é geométrica com proporção comum\(r=3\).
- A sequência é geométrica com proporção comum\(d=\frac{1}{4}\).
- A sequência não é geométrica. Não há uma proporção comum.
Determine se cada sequência é geométrica. Em caso afirmativo, indique a proporção comum.
- \(-150,-30,-15,-5,-\frac{5}{2}, 0, \dots\)
- \(5,10,20,40,80,160, \dots\)
- \(8,4,2,1, \frac{1}{2}, \frac{1}{4}, \ldots\)
- Responda
-
- A sequência não é geométrica. Não há uma proporção comum.
- A sequência é geométrica com proporção comum\(r=2\).
- A sequência é geométrica com proporção comum\(r=\frac{1}{2}\).
Se soubermos o primeiro termo\(a_{1}\),, e a razão comum\(r\),, podemos listar um número finito de termos da sequência.
Escreva os primeiros cinco termos da sequência onde está o primeiro termo\(3\) e a proporção comum\(r=−2\).
Solução:
Começamos com o primeiro termo e o multiplicamos pela proporção comum. Em seguida, multiplicamos esse resultado pela proporção comum para obter o próximo termo, e assim por diante.
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {3} & {3 \cdot(-2)} & {-6 \cdot(-2)} & {12 \cdot(-2)} & {-24 \cdot(-2)} \\& {-6} & {12} & {-24} & {48}\end{array}\)
Resposta:
A sequência é\(3,-6,12,-24,48, \dots\)
Escreva os primeiros cinco termos da sequência onde está o primeiro termo\(7\) e a proporção comum\(r=−3\).
- Responda
-
\(7,-21,63,-189,567\)
Escreva os primeiros cinco termos da sequência onde está o primeiro termo\(6\) e a proporção comum\(r=−4\).
- Responda
-
\(6,-24,96,-384,1536\)
Encontre o termo geral (\(n\)ésimo termo) de uma sequência geométrica
Assim como encontramos uma fórmula para o termo geral de uma sequência e uma sequência aritmética, também podemos encontrar uma fórmula para o termo geral de uma sequência geométrica.
Vamos escrever os primeiros termos da sequência em que está o primeiro termo\(a_{1}\) e a proporção comum\(r\). Em seguida, procuraremos um padrão.
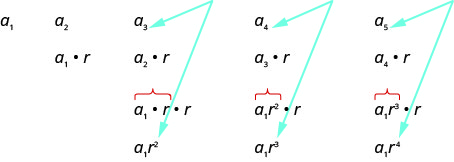
Ao procurarmos um padrão nos cinco termos acima, vemos que cada um dos termos começa com\(a_{1}\).
O primeiro termo,\(a_{1}\), não é multiplicado por nenhum\(r\). No segundo termo, o\(a_{1}\) é multiplicado por\(r\). No terceiro termo, o\(a_{1}\) é multiplicado por\(r\) duas vezes (\(r⋅r\)ou\(r^{2}\)). No quarto termo, o\(a_{1}\) é multiplicado por\(r\) três vezes (\(r⋅r⋅r\)ou\(r^{3}\)) e no quinto termo, o\(a_{1}\) é multiplicado por\(r\) quatro vezes. Em cada termo, o número de vezes\(a_{1}\) multiplicado por\(r\) é um a menos que o número do termo. Isso nos leva ao seguinte
\(a_{n}=a_{1} r^{n-1}\)
O termo geral de uma sequência geométrica com o primeiro termo\(a_{1}\) e a razão comum\(r\) é
\(a_{n}=a_{1} r^{n-1}\)
Usaremos essa fórmula no próximo exemplo para encontrar o décimo quarto termo de uma sequência.
Encontre o décimo quarto termo de uma sequência em que o primeiro termo é\(64\) e a proporção comum é\(r=\frac{1}{2}\).
Solução:
\(a_{n}=a_{1} r^{n-1}\)
Para encontrar o décimo quarto termo\(a_{14}\),, use a fórmula com\(a_{1}=64\)\(r=\frac{1}{2}\) e.
\(a_{14}=64\left(\frac{1}{2}\right)^{14-1}\)
Substitua os valores.
\(a_{14}=64\left(\frac{1}{2}\right)^{13}\)
Simplifique.
\(a_{14}=\frac{1}{128}\)
Encontre o décimo terceiro termo de uma sequência em que o primeiro termo está\(81\) e a proporção comum é\(r=\frac{1}{3}\).
- Responda
-
\(\frac{1}{6,561}\)
Encontre o décimo segundo termo de uma sequência em que o primeiro termo é\(256\) e a proporção comum é\(r=\frac{1}{4}\).
- Responda
-
\(\frac{1}{16,384}\)
Às vezes, não sabemos a proporção comum e devemos usar as informações fornecidas para encontrá-la antes de encontrarmos o termo solicitado.
Encontre o décimo segundo termo da sequência\(3, 6, 12, 24, 48, 96, …\) Encontre o termo geral da sequência.
Solução:
Para encontrar o décimo segundo termo, usamos a fórmula e\(a_{n}=a_{1} r^{n-1}\), portanto, precisamos primeiro determinar\(a_{1}\) a proporção comum\(r\).
O primeiro termo é três.
\(3,6,12,24,48,96, \dots\)
\(a_{1}=3\)
Encontre a proporção comum.
\(\begin{array}{l}{\frac{6}{3} \quad \frac{12}{6} \quad \frac{24}{12} \quad \frac{48}{24} \quad \frac{96}{48}} \\ {2 \:\:\:\quad 2 \quad \:\:2 \quad\:\:\: 2 \:\:\quad \:2} \\ {\text { The common ratio is } r=2}\end{array}\)
Para encontrar o décimo segundo termo\(a_{12}\), use a fórmula com\(a_{1}=3\)\(r=2\) e.
\(a_{n}=a_{1} r^{n-1}\)
Substitua os valores.
\(a_{12}=3 \cdot 2^{12-1}\)
Simplifique.
\(a_{12}=3 \cdot 2^{11}\)
\(a_{12}=6,144\)
Encontre o termo geral. Usamos a fórmula com\(a_{1}=3\)\(r=2\) e.
\(a_{n}=a_{1} r^{n-1}\)
\(a_{n}=3(2)^{n-1}\)
Encontre o nono termo da sequência\(6, 18, 54, 162, 486, 1,458, … \) Em seguida, encontre o termo geral da sequência.
- Responda
-
\(a_{9}=39,366 .\)O termo geral é\(a_{n}=6(3)^{n-1}\).
Encontre o décimo primeiro termo da sequência\(7, 14, 28, 56, 112, 224, …\) Em seguida, encontre o termo geral da sequência.
- Responda
-
\(a_{11}=7,168 .\)O termo geral é\(a_{n}=7(2)^{n-1}\).
Encontre a soma dos primeiros\(n\) termos de uma sequência geométrica
Encontramos a soma das sequências gerais e da sequência aritmética. Agora faremos o mesmo para sequências geométricas. A soma,\(S_{n}\), dos primeiros\(n\) termos de uma sequência geométrica é escrita como\(S_{n}=a_{1}+a_{2}+a_{3}+\ldots+a_{n}\). Podemos escrever essa soma começando com o primeiro termo\(a_{1}\), e continuar multiplicando por\(r\) para obter o próximo termo como:
\(S_{n}=a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}\)
Vamos também multiplicar os dois lados da equação por\(r\).
\(r S_{n}=a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n}\)
Em seguida, subtraímos essas equações. Veremos que, quando subtrairmos, todos, exceto o primeiro termo da equação superior e o último termo da equação inferior, subtraem para zero.
\(\begin{aligned} S_{n}&= a_{1}+a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1} \\ r S_{n} &= a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1}+a_{1} r^{n}\\\hline S_{n}-r S_{n} &= a_{1} -a_{1}r^{n} \end{aligned}\)
Nós consideramos os dois lados.
\(S_{n}(1-r)=a_{1}\left(1-r^{n}\right)\)
Para obter a fórmula para\(S_{n}\), divida os dois lados por\((1-r)\).
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
A soma,\(S_{n}\), dos primeiros\(n\) termos de uma sequência geométrica é
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
onde\(a_{1}\) é o primeiro termo e\(r\) é a proporção comum, e não\(r\) é igual a um.
Aplicamos essa fórmula no próximo exemplo, onde os primeiros termos da sequência são fornecidos. Observe que a soma de uma sequência geométrica normalmente fica muito grande quando a proporção comum é maior que um.
Encontre a soma dos primeiros\(20\) termos da sequência geométrica\(7, 14, 28, 56, 112, 224, …\)
Solução:
Para encontrar a soma, usaremos a fórmula\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\). Nós sabemos\(a_{1}=7\)\(r=2\), e\(n=20\),
Conhecendo e\(a_{1}=7, r=2\)\(n=20\), use a fórmula da soma.
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
Substitua os valores.
\(S_{20}=\frac{7\left(1-2^{20}\right)}{1-2}\)
Simplifique.
\(S_{20}=7,340,025\)
Encontre a soma dos primeiros\(20\) termos da sequência geométrica\(3, 6, 12, 24, 48, 96, …\)
- Responda
-
\(3,145,725\)
Encontre a soma dos primeiros\(20\) termos da sequência geométrica\(6, 18, 54, 162, 486, 1,458, …\)
- Responda
-
\(10,460,353,200\)
No próximo exemplo, recebemos a soma em notação de soma. Embora seja possível adicionar todos os termos, na maioria das vezes é mais fácil usar a fórmula para encontrar a soma dos primeiros\(n\) termos.
Para usar a fórmula, precisamos\(r\). Podemos encontrá-lo escrevendo os primeiros termos da sequência e encontrando sua proporção. Outra opção é perceber que na notação somatória, uma sequência é escrita na forma\(\sum_{i=1}^{k} a(r)^{i}\), onde\(r\) está a proporção comum.
Encontre a soma:\(\sum_{i=1}^{15} 2(3)^{i}\).
Solução:
Para encontrar a soma, usaremos a fórmula\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\), que requer\(a_{1}\)\(r\) e. Escreveremos alguns dos termos, para que possamos obter as informações necessárias.
 |
|
| Escreva os primeiros termos. | 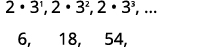 |
| Identifique\(a_{1}\). |  |
| Encontre a proporção comum. |  |
| Sabendo\(a_{1}=6\)\(r=3\), e\(n=15\), use a fórmula da soma. | 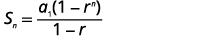 |
| Substitua os valores. | 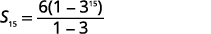 |
| Simplifique. | 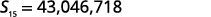 |
Encontre a soma:\(\sum_{i=1}^{15} 6(2)^{i}\).
- Responda
-
\(393,204\)
Encontre a soma:\(\sum_{i=1}^{10} 5(2)^{i}\).
- Responda
-
\(10,230\)
Encontre a soma de uma série geométrica infinita
Se pegarmos uma sequência geométrica e adicionarmos os termos, teremos uma soma que é chamada de série geométrica. Uma série geométrica infinita é uma soma infinita cujo primeiro termo é\(a_{1}\) e a razão comum é\(r\) e está escrito
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
Uma série geométrica infinita é uma soma infinita cujo primeiro termo é\(a_{1}\) e a razão comum é\(r\) e está escrito
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\dots\)
Sabemos como encontrar a soma dos primeiros\(n\) termos de uma série geométrica usando a fórmula,\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\). Mas como podemos encontrar a soma de uma soma infinita?
Vamos dar uma olhada na série geométrica infinita\(3+6+12+24+48+96+….\). Cada termo fica cada vez maior, então faz sentido que a soma do número infinito de termos fique maior. Vamos dar uma olhada em algumas somas parciais desta série. Nós vemos\(a_{1}=3\) e\(r=2\)
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{3\left(1-2^{10}\right)}{1-2}} & {S_{30}=\frac{3\left(1-2^{30}\right)}{1-2}} & {S_{50}=\frac{3\left(1-2^{50}\right)}{1-2}} \\ {S_{10}=3,069} & {S_{30}=3,221,225,469} & {S_{50}\approx 3.38 \times 10^{15}}\end{array}\)
À medida\(n\) que fica cada vez maior, a soma fica cada vez maior. Isso é verdade quando\(|r|≥1\) e chamamos a série de divergente. Não podemos encontrar a soma de uma série geométrica infinita quando\(|r|≥1\).
Vejamos uma série geométrica infinita cuja proporção comum é uma fração menor que um,
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\ldots\). Aqui, os termos ficam cada vez menores à\(n\) medida que aumentam. Vamos dar uma olhada em algumas somas finitas desta série. Nós vemos\(a_{1}=\frac{1}{2}\)\(r=\frac{1}{2}\) e.
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{10}\right)}{1-\frac{1}{2}}} & {S_{20}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{20}\right)}{1-\frac{1}{2}}} & {S_{30}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{30}\right)}{1-\frac{1}{2}}} \\ {S_{10}\approx 0.9990234375} & {S_{20}\approx 0.9999990463} & {S_{30}\approx 0.9999999991}\end{array}\)
Observe que a soma fica cada vez maior, mas também se aproxima cada vez mais de um. Quando\(|r|<1\), a expressão\(r^{n}\) fica cada vez menor. Nesse caso, chamamos a série de convergente. À medida que\(n\) se aproxima do infinito, (fica infinitamente grande),\(r^{n}\) fica cada vez mais perto de zero. Em nossa fórmula de soma, podemos\(r^{n}\) substituir o por zero e então obtemos uma fórmula para a soma,\(S\), para uma série geométrica infinita quando\(|r|<1\).
\(\begin{aligned} S_{n} &=\frac{a_{1}\left(1-r^{n}\right)}{1-r} \\ S &=\frac{a_{1}(1-0)}{1-r} \\ S &=\frac{a_{1}}{1-r} \end{aligned}\)
Essa fórmula nos dá a soma da sequência geométrica infinita. Observe\(S\) que o não tem o subscrito\(n\),\(S_{n}\) pois não estamos adicionando um número finito de termos.
Para uma série geométrica infinita cujo primeiro termo é uma\(a_{1}\) proporção comum\(r\),
Se\(|r|<1\), a soma é
\(S=\frac{a_{1}}{1-r}\)
Se\(|r|≥1\), a série geométrica infinita não tem uma soma. Dizemos que a série diverge.
Encontre a soma das séries geométricas infinitas\(54+18+6+2+\frac{2}{3}+\frac{2}{9}+\ldots\)
Solução:
Para encontrar a soma, primeiro temos que verificar se é a razão comum\(|r|<1\) e depois podemos usar a fórmula da soma\(S=\frac{a_{1}}{1-r}\).
Encontre a proporção comum.
\(\begin{array}{ll}{r=\frac{18}{54}} & {r=\frac{6}{18} \dots} \\ {r=\frac{1}{3}} & {r=\frac{1}{3} \quad|r|<1}\end{array}\)
Identifique\(a_{1}\).
\(a_{1}=54\)
Sabendo\(a_{1}=54, r=\frac{1}{3}\), use a fórmula da soma.
\(S=\frac{a_{1}}{1-r}\)
Substitua os valores.
\(S=\frac{54}{1-\frac{1}{3}}\)
Simplifique.
\(S=81\)
Resposta:
\(S=80\)
Encontre a soma das séries geométricas infinitas\(48+24+12+6+3+\frac{3}{2}+\dots\)
- Responda
-
\(96\)
Encontre a soma das séries geométricas infinitas\(64+16+4+1+\frac{1}{4}+\frac{1}{16}+\dots\)
- Responda
-
\(\frac{256}{3}\)
Um uso interessante de séries geométricas infinitas é escrever um decimal repetido como uma fração.
Escreva o decimal repetido\(0.5\) como uma fração.
Solução:
Reescreva a\(0.5\) exibição dos cinco repetidos. Use o valor posicional para reescrever isso como uma soma. Esta é uma série geométrica infinita.
0,5555555555 55 55\(\ldots\)
\(0.5+0.05+0.005+0.0005+\dots\)
Encontre a proporção comum.
\(\begin{array}{ll}{r=\frac{0.05}{0.5}} & {r=\frac{0.005}{0.05} \dots} \\ {r=0.1} & {r=0.1 \quad|r|<1}\end{array}\)
Identifique\(a_{1}\)
\(a_{1}=0.5\)
Sabendo\(a_{1}=0.5 ,r=0.1\), use a fórmula da soma.
\(S=\frac{a_{1}}{1-r}\)
Substitua os valores.
\(S=\frac{0.5}{1-0.1}\)
Simplifique.
\(S=\frac{0.5}{0.9}\)
Multiplique o numerador e o denominador por\(10\).
\(S=\frac{5}{9}\)
Somos solicitados a encontrar a forma fracionária.
\(0.5 = \frac{5}{9}\)
Escreva o decimal repetido\(0.4\) como uma fração.
- Responda
-
\(\frac{4}{9}\)
Escreva o decimal repetido\(0.8\) como uma fração.
- Responda
-
\(\frac{8}{9}\)
Aplique sequências e séries geométricas no mundo real
Uma aplicação de sequências geométricas tem a ver com os gastos do consumidor. Se um desconto fiscal for concedido a cada família, o efeito na economia é muitas vezes o valor do desconto individual.
O governo decidiu conceder um desconto\(1,000\) fiscal de $ para cada família, a fim de estimular a economia. As estatísticas do governo dizem que cada família gastará\(80\)% do desconto em bens e serviços. As empresas e indivíduos que se beneficiaram dessa\(80\)% gastarão então\(80\)% do que receberam e assim por diante. O resultado é chamado de efeito multiplicador. Qual é o efeito total do desconto na economia?
Solução:
Toda vez que o dinheiro vai para a economia,\(80\)% dele é gasto e, em seguida, está na economia para ser gasto. Novamente,\(80\)% desse dinheiro é gasto na economia novamente. Essa situação continua e nos leva a uma série geométrica infinita.
\(1000+1000(0.8)+1000(0.8)^{2}+\ldots\)
Aqui, o primeiro termo é\(1,000, a_{1}=1000\). A proporção comum é\(0.8, r=0.8\). Podemos avaliar essa soma desde então\(0.8<1\). Usamos a fórmula para a soma em uma série geométrica infinita.
\(S=\frac{a_{1}}{1-r}\)
Substitua os valores,\(a_{1}=1,000\)\(r=0.8\) e.
\(S=\frac{1,000}{1-0.8}\)
Avalie.
\(S=5,000\)
Resposta:
O efeito total do $\(1,000\) recebido por cada família será um\(5,000\) crescimento de $ na economia.
Qual é o efeito total na economia de um desconto fiscal do governo de $\(1,000\) para cada família, a fim de estimular a economia se cada família gastar\(90\)% do desconto em bens e serviços?
- Responda
-
$\(10,000\)
Qual é o efeito total na economia de um desconto fiscal do governo de $\(500\) para cada família, a fim de estimular a economia se cada família gastar\(85\)% do desconto em bens e serviços?
- Responda
-
$\(3,333.33\)
Examinamos uma fórmula de juros compostos em que um principal,\(P\), é investido a uma taxa de juros,\(r\), por\(t\) anos. O novo saldo,\(A\), é\(A=P\left(1+\frac{r}{n}\right)^{n t}\) quando os juros são compostos\(n\) vezes por ano. Essa fórmula se aplica quando uma quantia fixa é investida antecipadamente e nos informa o valor após um determinado período de tempo.
Uma anuidade é um investimento que é uma sequência de depósitos periódicos iguais. Analisaremos as anuidades que pagam os juros no momento dos depósitos. À medida que desenvolvemos a fórmula para o valor de uma anuidade, vamos deixar\(n=1\). Isso significa que há um depósito por ano.
\(\begin{aligned} &A =P\left(1+\frac{r}{n}\right)^{n t} \\ \text { Let } n=1 .\quad & A=P\left(1+\frac{r}{1}\right)^{1 t} \\ \text { Simplify. }\quad & A=P(1+r)^{t} \end{aligned}\)
Suponha que\(P\) dólares sejam investidos no final de cada ano. Um ano depois, esse depósito vale\(P(1+r)^{1}\) dólares e outro ano depois vale\(P(1+r)^{2}\) dólares. Depois de\(t\) anos, valerá\(P(1+r)^{t}\) dólares.
| Fim do ano\(1\) | Fim do ano\(2\) | Fim do ano\(3\) | |
|---|---|---|---|
| Primeiro depósito\(P\) no final do ano\(1\) | \ (1\) ">\(P\) | \ (2\) ">Quantia\(1\) um ano depois\(P(1+r)^{1}\) | \ (3\) ">Quantidade de\(2\) anos depois\(P(1+r)^{2}\) |
| \(2\)Depósito\(P\) final no final do ano\(2\) | \ (1\) "> | \ (2\) ">\(P\) | \ (3\) ">Quantia\(1\) ano depois\(P(1+r)^{1}\) |
| \(3\)3º\(P\) Depósito no final do ano\(3\) | \ (1\) "> | \ (2\) "> | \ (3\) ">\(P\) |
Depois de três anos, o valor da anuidade é
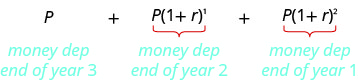
É a soma dos termos de uma sequência geométrica em que o primeiro termo é\(P\) e a razão comum é\(1+r\). Substituímos esses valores na fórmula da soma. Tenha cuidado, temos dois usos diferentes do\(r\). A fórmula\(r\) in the sum é a proporção comum da sequência. Nesse caso, é\(1+r\) aí que\(r\) está a taxa de juros.
\(\begin{aligned} &S_{t} =\frac{a_{1}\left(1-r^{t}\right)}{1-r} \\ \text { Substitute in the values. }\quad & S_{t}=\frac{P\left(1-(1+r)^{t}\right)}{1-(1+r)} \\ \text { Simplify. }\quad & S_{t} =\frac{P\left(1-(1+r)^{t}\right)}{-r} \\ &S_{t} =\frac{P\left((1+r)^{t}-1\right)}{r} \end{aligned}\)
Lembre-se de que nossa premissa era que um depósito era feito no final de cada ano.
Podemos adaptar essa fórmula para\(n\) depósitos feitos por ano e os juros são compostos\(n\) vezes por ano.
Para um principal\(P\),, investido no final de um período composto, com uma taxa de juros\(r\), que é composta\(n\) vezes por ano, o novo saldo\(A\), após\(t\) anos, é
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Novos pais decidem investir $\(100\) por mês em uma anuidade para sua filha. A conta pagará\(5\)% de juros por ano, que são compostos mensalmente. Quanto estará na conta da criança em seu aniversário de dezoito anos?
Solução:
Para encontrar a fórmula da anuidade\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\), precisamos identificar\(P, r, n\),\(t\) e.
Identifique\(P\) o valor investido a cada mês.
\(P=100\)
Identifique\(r\) a taxa de juros anual, na forma decimal.
\(r=0.05\)
Identifique\(n\) o número de vezes que o depósito será feito e os juros compostos a cada ano.
\(n=12\)
\(t\)Identifique o número de anos.
\(t=18\)
Conhecendo\(P=100, r=0.05, n=12\) e\(t=18\), use a fórmula da soma.
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Substitua os valores.
\(A_{t}=\frac{100\left(\left(1+\frac{0.05}{12}\right)^{12.18}-1\right)}{\frac{0.05}{12}}\)
Use a calculadora para avaliar. Certifique-se de usar parênteses conforme necessário.
\(A_{t}=34.920 .20\)
Resposta:
A criança terá $\(34,920.20\)
Os novos avós decidem investir $\(200\) por mês em uma anuidade para o neto. A conta pagará\(5\)% de juros por ano, que são compostos mensalmente. Quanto estará na conta da criança em seu vigésimo primeiro aniversário?
- Responda
-
$\(88,868.36\)
Arturo acabou de conseguir seu primeiro emprego em tempo integral depois de se formar na faculdade com a idade\(27\). Ele decidiu investir $\(200\) por mês em um IRA (uma anuidade). Os juros sobre a anuidade são\(8\)%, que são compostos mensalmente. Quanto estará na conta do Arturo quando ele se aposentar em seu sexagésimo sétimo aniversário?
- Responda
-
$\(698,201.57\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com sequências.
Conceitos-chave
- Termo geral (\(n\)ésimo termo) de uma sequência geométrica: O termo geral de uma sequência geométrica com o primeiro termo\(a_{1}\) e a proporção comum\(r\) é
\(a_{n}=a_{1} r^{n-1}\)
- Soma dos primeiros\(n\) termos de uma série geométrica: A soma,\(S_{n}\), dos\(n\) termos de uma sequência geométrica é
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
onde\(a_{1}\) está o primeiro termo e\(r\) é a proporção comum. Série Geométrica Infinita: Uma série geométrica infinita é uma soma infinita cujo primeiro termo é\(a_{1}\) uma proporção comum é\(r\) e está escrito\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
- Soma de uma série geométrica infinita: Para uma série geométrica infinita cujo primeiro termo é\(a_{1}\) uma proporção comum\(r\),
Se\(|r|<1\), a soma é
\(S=\frac{a_{1}}{1-r}\)
Dizemos que a série converge.
Se\(|r|≥1\), a série geométrica infinita não tem uma soma. Dizemos que a série diverge.
- Valor de uma anuidade com juros compostos \(n\)vezes por ano: Para um principal,\(P\), investido no final de um período composto, com uma taxa de juros,\(r\), que é composta\(n\) vezes por ano, o novo saldo,\(A\), após \(t\)anos, é
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Glossário
- anuidade
- Uma anuidade é um investimento que é uma sequência de depósitos periódicos iguais.
- proporção comum
- A razão entre termos consecutivos em uma sequência geométrica\(\frac{a_{n}}{a_{n-1}}\),\(r\), é a razão comum, onde\(r\) maior ou igual a dois.
- sequência geométrica
- Uma sequência geométrica é uma sequência em que a razão entre termos consecutivos é sempre a mesma
- série geométrica infinita
- Uma série geométrica infinita é uma sequência geométrica infinita de soma infinita.


