12.3: Sequências aritméticas
- Page ID
- 183081
Ao final desta seção, você poderá:
- Determine se uma sequência é aritmética
- Encontre o termo geral (\(n\)ésimo termo) de uma sequência aritmética
- Encontre a soma dos primeiros\(n\) termos de uma sequência aritmética
Antes de começar, faça este teste de prontidão.
- Avalie\(4n−1\) os números inteiros\(1, 2, 3\)\(4\) e.
Se você perdeu esse problema, consulte o Exemplo 1.6. - Resolva o sistema de equações:\(\left\{\begin{array}{l}{x+y=7} \\ {3 x+4 y=23}\end{array}\right.\).
Se você perdeu esse problema, consulte o Exemplo 4.9. - Se\(f(n)=\frac{n}{2}(3 n+5)\), encontre\(f(1)+f(20)\).
Se você perdeu esse problema, consulte o Exemplo 3.49.
Determine se uma sequência é aritmética
A última seção introduziu sequências e agora veremos dois tipos específicos de sequências, cada uma com propriedades especiais. Nesta seção, veremos as sequências aritméticas e, na próxima seção, as sequências geométricas.
Uma sequência aritmética é uma sequência em que a diferença entre termos consecutivos é constante. A diferença entre termos consecutivos em uma sequência aritmética, a_ {n} -a_ {n-1}\(d\), é a diferença comum, para\(n\) maior ou igual a dois.
Uma sequência aritmética é uma sequência em que a diferença entre termos consecutivos é sempre a mesma.
A diferença entre termos consecutivos, a_ {n} -a_ {n-1}\(d\), é a diferença comum, para\(n\) maior ou igual a dois.
Determine se cada sequência é aritmética. Em caso afirmativo, indique a diferença comum.
- \(5,9,13,17,21,25, \dots\)
- \(4,9,12,17,20,25, \dots\)
- \(10,3,-4,-11,-18,-25, \dots\)
Solução:
Para determinar se a sequência é aritmética, encontramos a diferença dos termos consecutivos mostrados.
uma.\(\begin{array}{cccccc}{5,} & {9,} & {13,} & {17} & {21,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-5} & {13-9} & {17-13} & {21-17} & {25-21} \\ & {4} & {4} & {4} & {4}&{4}\end{array}\)
A sequência é aritmética. A diferença comum é\(d=4\).
b.\(\begin{array}{cccccc}{4,} & {9,} & {12,} & {17} & {20,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-4} & {12-9} & {17-12} & {20-17} & {25-20} \\ & {2} & {3} & {5} & {3}&{5}\end{array}\)
A sequência não é aritmética, pois todas as diferenças entre os termos consecutivos não são as mesmas. Não há nenhuma diferença comum.
c.\(\begin{array}{cccccc}{10,} & {3,} & {-4,} & {-11} & {-18,} & {-25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {3-10} & {-4-3} & {-11-(-4)} & {-18-(-11)} & {-25-(-18)} \\ & {-7} & {-7} & {-7} & {-7}&{-7}\end{array}\)
Resposta:
A sequência é aritmética. A diferença comum é\(d=-7\).
Determine se cada sequência é aritmética. Em caso afirmativo, indique a diferença comum.
- \(9,20,31,42,53,64, \dots\)
- \(12,6,0,-6,-12,-18, \dots\)
- \(7,1,10,4,13,7, \dots\)
- Responda
-
- A sequência é aritmética com diferença comum\(d=11\).
- A sequência é aritmética com diferença comum\(d=-6\).
- A sequência não é aritmética, pois todas as diferenças entre os termos consecutivos não são as mesmas.
Determine se cada sequência é aritmética. Em caso afirmativo, indique a diferença comum.
- \(-4,4,2,10,8,16, \dots\)
- \(-3,-1,1,3,5,7, \dots\)
- \(7,2,-3,-8,-13,-18, \dots\)
- Responda
-
- A sequência não é aritmética, pois todas as diferenças entre os termos consecutivos não são as mesmas.
- A sequência é aritmética com diferença comum\(d=2\).
- A sequência é aritmética com diferença comum\(d=−5\).
Se soubermos o primeiro termo\(a_{1}\),, e a diferença comum\(d\), podemos listar um número finito de termos da sequência.
Escreva os primeiros cinco termos da sequência onde está o primeiro termo\(5\) e a diferença comum\(d=−6\).
Solução:
Começamos com o primeiro termo e adicionamos a diferença comum. Em seguida, adicionamos a diferença comum a esse resultado para obter o próximo termo, e assim por diante.
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {5} & {5+(-6)} & {-1+(-6)} & {-7+(-6)} & {-13+(-6)} \\ {}&{-1} & {-7} & {-13} & {-19}\end{array}\)
Resposta:
A sequência é\(5,-1,-7,-13,-19, \dots\)
Escreva os primeiros cinco termos da sequência onde está o primeiro termo\(7\) e a diferença comum\(d=−4\).
- Responda
-
\(7,3,-1,-5,-9, \dots\)
Escreva os primeiros cinco termos da sequência onde está o primeiro termo\(11\) e a diferença comum\(d=−8\).
- Responda
-
\(11,3,-5,-13,-21, \dots\)
Encontre o termo geral (\(n\)ésimo termo) de uma sequência aritmética
Assim como encontramos uma fórmula para o termo geral de uma sequência, também podemos encontrar uma fórmula para o termo geral de uma sequência aritmética.
Vamos escrever os primeiros termos de uma sequência em que o primeiro termo é\(a_{1}\) e a diferença comum é\(d\). Em seguida, procuraremos um padrão.
Ao procurarmos um padrão, vemos que cada termo começa com\(a_{1}\).
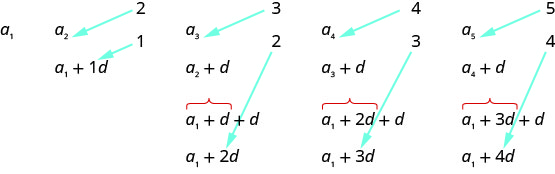
O primeiro termo é adicionado\(0d\) ao\(a_{1}\), o segundo termo adiciona\(1d\), o terceiro termo adiciona\(2d\), o quarto termo soma\(3d\) e o quinto termo adiciona\(4d\). O número dos\(ds\) que foram adicionados\(a_{1}\) é um a menos do que o número do termo. Isso nos leva ao seguinte
\(a_{n}=a_{1}+(n-1) d\)
O termo geral de uma sequência aritmética com o primeiro termo\(a_{1}\) e a diferença comum\(d\) é
\(a_{n}=a_{1}+(n-1) d\)
Usaremos essa fórmula no próximo exemplo para encontrar o 15º termo de uma sequência.
Encontre o décimo quinto termo de uma sequência em que o primeiro termo está\(3\) e a diferença comum é\(6\).
Solução:
\(\begin{array}{cc}{\text{To find the fifteenth term, }a_{15}\text{, use the formula with } a_{1}=3 \:\text{and} \:d=6.}&{a_{n}=a_{1}+(n-1) d} \\ {\text{Substitute in the values.}}&{a_{15}=3+(15-1) 6} \\{\text{Simplify.}}& {a_{15}=3+(14) 6} \\ {}&{a_{15}=87}\end{array}\)
Encontre o vigésimo sétimo termo de uma sequência em que o primeiro termo está\(7\) e a diferença comum é\(9\).
- Responda
-
\(241\)
Encontre o décimo oitavo termo de uma sequência em que o primeiro termo está\(13\) e a diferença comum é\(−7\).
- Responda
-
\(-106\)
Às vezes, não conhecemos o primeiro termo e devemos usar outras informações para encontrá-lo antes de encontrarmos o termo solicitado.
Encontre o décimo segundo termo de uma sequência em que o sétimo termo está\(10\) e a diferença comum é\(−2\). Dê a fórmula para o termo geral.
Solução:
Para encontrar primeiro o primeiro termo\(a_{1}\), use a fórmula com\(a_{7}=10\)\(n=7\),\(d=−2\) e. Substitua os valores. Simplifique.
\(a_{n}=a_{1}+(n-1) d\)
\(10=a_{1}+(7-1)(-2)\)
\(10=a_{1}+(6)(-2)\)
\(10=a_{1}-12\)
\(a_{1}=22\)
Encontre o décimo segundo termo\(a_{12}\),, usando a fórmula com\(a_{1}=22\)\(n=12\),\(d=-2\) e. Substitua os valores. Simplifique.
\(a_{n}=a_{1}+(n-1) d\)
\(a_{12}=22+(12-1)(-2)\)
\(a_{12}=22+(11)(-2)\)
\(a_{12}=0\)
O décimo segundo termo da sequência é\(0, a_{12}=0\)
Para encontrar o termo geral, substitua os valores na fórmula.
\(a_{n}=a_{1}+(n-1) d\)
\(a_{n}=22+(n-1)(-2)\)
\(a_{n}=22-2 n+2\)
Resposta:
O termo geral é\(a_{n}=-2 n+24\)
Encontre o décimo primeiro termo de uma sequência em que o nono termo está\(8\) e a diferença comum é\(−3\). Dê a fórmula para o termo geral.
- Responda
-
\(a_{11}=2 .\)O termo geral é\(a_{n}=-3 n+35\)
Encontre o décimo nono termo de uma sequência em que o quinto termo é\(1\) e a diferença comum é\(−4\) .Forneça a fórmula para o termo geral.
- Responda
-
\(a_{19}=-55 .\)O termo geral é\(a_{n}=-4 n+21\)
Às vezes, as informações fornecidas nos levam a duas equações em duas incógnitas. Em seguida, usamos nossos métodos para resolver sistemas de equações para encontrar os valores necessários.
Encontre o primeiro termo e a diferença comum de uma sequência em que o quinto termo é\(19\) e o décimo primeiro termo está\(37\). Dê a fórmula para o termo geral.
Solução:
Como conhecemos dois termos, podemos criar um sistema de equações usando a fórmula para o termo geral.
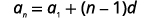 |
|
| Sabemos o valor de\(a_{5}\) e\(a_{11}\), então usaremos\(n=5\)\(n=11\) e. | 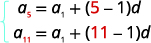 |
Substitua os valores,\(a_{5}=19\)\(a_{11}=37\) e. |
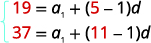 |
| Simplifique. | 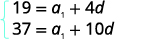 |
| Prepare-se para eliminar o\(a_{1}\) termo multiplicando a equação superior por\(−1\). Adicione as equações. |
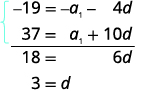 |
| Substituindo de\(d=3\) volta na primeira equação. | 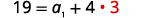 |
| Resolva para\(a_{1}\). |  |
| Use a fórmula com\(a_{1}=7\)\(d=3\) e. | 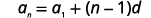 |
| Substitua os valores. | 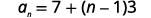 |
| Simplifique. | 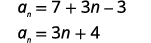 |
| O primeiro termo é\(a_{1}=7\). A diferença comum é\(d=3\). |
|
| O termo geral da sequência é\(a_{n}=3n+4\). |
Resposta:
O termo geral da sequência é\(a_{n}=3n+4\).
Encontre o primeiro termo e a diferença comum de uma sequência em que o quarto termo é\(17\) e o décimo terceiro termo está\(53\). Dê a fórmula para o termo geral.
- Responda
-
\(a_{1}=5, d=4 .\)O termo geral é\(a_{n}=4 n+1\).
Encontre o primeiro termo e a diferença comum de uma sequência em que o terceiro termo é\(2\) e o décimo segundo termo é\(−25\). Dê a fórmula para o termo geral.
- Responda
-
\(a_{1}=8, d=-3 .\)O termo geral é\(a_{n}=-3 n+11\).
Encontre a soma dos primeiros\(n\) termos de uma sequência aritmética
Assim como acontece com as sequências gerais, geralmente é útil encontrar a soma de uma sequência aritmética. A soma,\(S_{n}\), dos primeiros\(n\) termos de qualquer sequência aritmética é escrita como\(S_{n} =a_{1} +a_{2} +a_{3} +\ldots +a_{n}\). Encontrar a soma simplesmente adicionando todos os termos pode ser entediante. Assim, também podemos desenvolver uma fórmula para encontrar a soma de uma sequência usando o primeiro e o último termo da sequência.
Podemos desenvolver essa nova fórmula escrevendo primeiro a soma começando com o primeiro termo\(a_{1}\), e continuar adicionando a\(d\) para obter o próximo termo como:
\(S_{n}=a_{1}+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n}\).
Também podemos reverter a ordem dos termos e escrever a soma começando com\(a_{n}\) e continuar subtraindo\(d\) para obter o próximo termo como
\(S_{n}=a_{n}+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1}\).
Se somarmos essas duas expressões para a soma dos primeiros\(n\) termos de uma sequência aritmética, podemos derivar uma fórmula para a soma dos primeiros\(n\) termos de qualquer série aritmética.
\(\begin{aligned} &S_{n}= a_{1} \quad+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n} \\+&S_{n} =a_{n} \quad+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1} \\ \hline \\ &2S_{n}=(a_{1}+a_{n})+(a_{1}+a_{n})+(a_{1}+a_{n})+\dots+(a_{1}+a_{n}) \end{aligned}\)
Como há\(n\) somas de\((a_{1}+a_{n})\) no lado direito da equação, reescrevemos o lado direito como\(n(a_{1}+a_{n})\).
\(2 S_{n}=n\left(a_{1}+a_{n}\right)\)
Nós dividimos por dois para resolver\(S_{n}\).
\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
Isso nos dá uma fórmula geral para a soma dos primeiros\(n\) termos de uma sequência aritmética.
A soma,\(S_{n}\), dos primeiros\(n\) termos de uma progressão aritmética é
\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
onde\(a_{1}\) é o primeiro termo e\(a_{n}\) é o\(n\) décimo termo.
Aplicamos essa fórmula no próximo exemplo, onde os primeiros termos da sequência são fornecidos.
Encontre a soma dos primeiros\(30\) termos da progressão aritmética:\(8, 13, 18, 23, 28, …\)
Solução:
Para encontrar a soma, usaremos a fórmula\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). Nós sabemos\(a_{1}=8, d=5\) e\(n=30\), mas precisamos encontrar\(a_{n}\) para usar a fórmula da soma.
Descubra\(a_{n}\) onde\(a_{1}=8, d=5\)\(n=30\) e. Simplifique.
\(\begin{aligned} a_{n} &=a_{1}+(n-1) d \\ a_{30} &=8+(30-1) 5 \\ a_{30} &=8+(29) 5 \\ a_{30} &=153 \end{aligned}\)
Conhecendo e\(a_{1}=8, n=30\)\(a_{30}=153\), use a fórmula da soma. Substitua os valores. Simplifique. Simplifique.
\(\begin{aligned} S_{n} &=\frac{n}{2}\left(a_{1}+a_{n}\right) \\ S_{30} &=\frac{30}{2}(8+153) \\ S_{30} &=15(161) \\ S_{30} &=2,415 \end{aligned}\)
Encontre a soma dos primeiros\(30\) termos da progressão aritmética:\(5, 9, 13, 17, 21, …\)
- Responda
-
\(1,890\)
Encontre a soma dos primeiros\(30\) termos da progressão aritmética:\(7, 10, 13, 16, 19, …\)
- Responda
-
\(1,515\)
No próximo exemplo, recebemos o termo geral para a sequência e somos solicitados a encontrar a soma dos primeiros\(50\) termos.
Encontre a soma dos primeiros\(50\) termos da progressão aritmética cujo termo geral é\(a_{n}=3n−4\).
Solução:
Para encontrar a soma, usaremos a fórmula\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). Nós sabemos\(n=50\), mas precisamos encontrar\(a_{1}\) e\(a_{n}\) para usar a fórmula da soma.
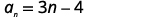 |
|
| Encontre\(a_{1}\), substituindo\(n=1\). | 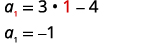 |
| Encontre\(a_{n}\) substituindo\(n=50\). | 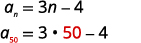 |
| Simplifique. | 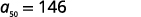 |
| Conhecer\(n=50, a_{1}=−1,\) e\(a_{50}=146\) usar a fórmula da soma. | 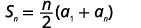 |
| Substitua os valores. | 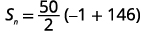 |
| Simplifique. | 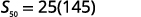 |
| Simplifique. | 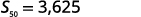 |
Encontre a soma dos primeiros\(50\) termos da progressão aritmética cujo termo geral é\(a_{n}=2n−5\).
- Responda
-
\(2,300\)
Encontre a soma dos primeiros\(50\) termos da progressão aritmética cujo termo geral é\(a_{n}=4n+3\).
- Responda
-
\(5,250\)
No próximo exemplo, recebemos a soma em notação de soma. Adicionar todos os termos seria entediante, então extraímos as informações necessárias para usar a fórmula para encontrar a soma dos primeiros\(n\) termos.
Encontre a soma:\(\sum_{i=1}^{25}(4 i+7)\).
Solução:
Para encontrar a soma, usaremos a fórmula\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). Nós sabemos\(n=25\), mas precisamos encontrar\(a_{1}\) e\(a_{n}\) para usar a fórmula da soma.
| Expanda a notação da soma. |
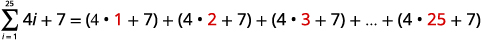
|
| Simplifique. |
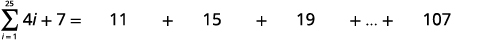
|
| Identifique\(a_{1}\). |  |
| Identifique\(a_{25}\). |

|
| Conhecer\(n=25, a_{1}=11\) e\(a_{25} = 107\) usar a fórmula da soma. |  |
| Substitua os valores. |  |
| Simplifique. |  |
| Simplifique. |  |
Encontre a soma:\(\sum_{i=1}^{30}(6 i-4)\).
- Responda
-
\(2,670\)
Encontre a soma:\(\sum_{i=1}^{35}(5 i-3)\).
- Responda
-
\(3,045\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com sequências aritméticas
Conceitos-chave
- Termo geral (\(n\)ésimo termo) de uma sequência aritmética
O termo geral de uma sequência aritmética com o primeiro termo\(a_{1}\) e a diferença comum\(d\) é\(a_{n}=a_{1}+(n-1) d\)
- Soma dos primeiros\(n\) termos de uma progressão aritmética
A soma\(S_{n}\),, dos primeiros\\(n\) termos de uma progressão aritmética, onde\(a_{1}\) é o primeiro termo e\(a_{n}\) o\(n\) ésimo termo é\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
Glossário
- sequência aritmética
- Uma sequência aritmética é uma sequência em que a diferença entre termos consecutivos é constante.
- diferença comum
- A diferença entre termos consecutivos em uma sequência aritmética\(a_{n}−a_{n−1}\),\(d\), é a diferença comum, para\(n\) maior ou igual a dois.


