Skip to main content
Global

12.2E: Exercícios

  1. Last updated
  2. Save as PDF
  • Page ID
    183062

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    A prática leva à perfeição

    Exercício\(\PageIndex{25}\) Write the First Few Terms of a Sequence

    Nos exercícios a seguir, escreva os primeiros cinco termos da sequência cujo termo geral é dado.

    1. \(a_{n}=2 n-7\)
    2. \(a_{n}=5 n-1\)
    3. \(a_{n}=3 n+1\)
    4. \(a_{n}=4 n+2\)
    5. \(a_{n}=2^{n}+3\)
    6. \(a_{n}=3^{n}-1\)
    7. \(a_{n}=3^{n}-2 n\)
    8. \(a_{n}=2^{n}-3 n\)
    9. \(a_{n}=\frac{2^{n}}{n^{2}}\)
    10. \(a_{n}=\frac{3^{n}}{n^{3}}\)
    11. \(a_{n}=\frac{4 n-2}{2^{n}}\)
    12. \(a_{n}=\frac{3 n+3}{3^{n}}\)
    13. \(a_{n}=(-1)^{n} \cdot 2 n\)
    14. \(a_{n}=(-1)^{n} \cdot 3 n\)
    15. \(a_{n}=(-1)^{n+1} n^{2}\)
    16. \(a_{n}=(-1)^{n+1} n^{4}\)
    17. \(a_{n}=\frac{(-1)^{n+1}}{n^{2}}\)
    18. \(a_{n}=\frac{(-1)^{n+1}}{2 n}\)
    Responda

    1. \(-5,-3,-1,1,3\)

    3. \(4,7,10,13,16\)

    5. \(5,7,11,19,35\)

    7. \(1,5,21,73,233\)

    9. \(2,1, \frac{8}{9}, 1, \frac{32}{25}\)

    11. \(1, \frac{3}{2}, \frac{5}{4}, \frac{7}{8}, \frac{9}{16}\)

    13. \(-2,4,-6,8,-10\)

    15. \(1,-4,9,-16,25\)

    17. \(1,-\frac{1}{4}, \frac{1}{9},-\frac{1}{16}, \frac{1}{25}\)

    Exercício\(\PageIndex{26}\) Find a Formula for the General Term (\(n\)th Term) of a Sequence

    Nos exercícios a seguir, encontre um termo geral para a sequência cujos primeiros cinco termos são mostrados.

    1. \(8,16,24,32,40, \dots\)
    2. \(7,14,21,28,35, \ldots\)
    3. \(6,7,8,9,10, \dots\)
    4. \(-3,-2,-1,0,1, \dots\)
    5. \(e^{3}, e^{4}, e^{5}, e^{6}, e^{7}, \ldots\)
    6. \(\frac{1}{e^{2}}, \frac{1}{e}, 1, e, e^{2}, \ldots\)
    7. \(-5,10,-15,20,-25, \dots\)
    8. \(-6,11,-16,21,-26, \dots\)
    9. \(-1,8,-27,64,-125, \dots\)
    10. \(2,-5,10,-17,26, \dots\)
    11. \(-2,4,-6,8,-10, \dots\)
    12. \(1,-3,5,-7,9, \dots\)
    13. \(\frac{1}{4}, \frac{1}{16}, \frac{1}{64}, \frac{1}{256}, \frac{1}{1,024}, \dots\)
    14. \(\frac{1}{1}, \frac{1}{8}, \frac{1}{27}, \frac{1}{64}, \frac{1}{125}, \dots\)
    15. \(-\frac{1}{2},-\frac{2}{3},-\frac{3}{4},-\frac{4}{5},-\frac{5}{6}, \dots\)
    16. \(-2,-\frac{3}{2},-\frac{4}{3},-\frac{5}{4},-\frac{6}{5}, \dots\)
    17. \(-\frac{5}{2},-\frac{5}{4},-\frac{5}{8},-\frac{5}{16},-\frac{5}{32}, \dots\)
    18. \(4, \frac{1}{2}, \frac{4}{27}, \frac{4}{64}, \frac{4}{125}, \dots\)
    Responda

    1. \(a_{n}=8 n\)

    3. \(a_{n}=n+5\)

    5. \(a_{n}=e^{n+2}\)

    7. \(a_{n}=(-1)^{n} 5 n\)

    9. \(a_{n}=(-1)^{n} n^{3}\)

    11. \(a_{n}=(-1)^{n} 2 n\)

    13. \(a_{n}=\frac{1}{4^{n}}\)

    15. \(a_{n}=-\frac{n}{n+1}\)

    17. \(-\frac{5}{2^{n}}\)

    Exercício\(\PageIndex{27}\) Use Factorial Notation

    Nos exercícios a seguir, usando notação fatorial, escreva os primeiros cinco termos da sequência cujo termo geral é dado.

    1. \(a_{n}=\frac{4}{n !}\)
    2. \(a_{n}=\frac{5}{n !}\)
    3. \(a_{n}=3 n !\)
    4. \(a_{n}=2 n !\)
    5. \(a_{n}=(2 n) !\)
    6. \(a_{n}=(3 n) !\)
    7. \(a_{n}=\frac{(n-1) !}{(n) !}\)
    8. \(a_{n}=\frac{n !}{(n+1) !}\)
    9. \(a_{n}=\frac{n !}{n^{2}}\)
    10. \(a_{n}=\frac{n^{2}}{n !}\)
    11. \(a_{n}=\frac{(n+1) !}{n^{2}}\)
    12. \(a_{n}=\frac{(n+1) !}{2 n}\)
    Responda

    1. \(4,2, \frac{2}{3}, \frac{1}{6}, \frac{1}{30}\)

    3. \(3,6,18,72,360\)

    5. \(2,24,720,40320,3628800\)

    7. \(1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}\)

    9. \(1, \frac{1}{2}, \frac{2}{3}, \frac{3}{2}, \frac{24}{5}\)

    11. \(2, \frac{3}{2}, \frac{8}{3}, \frac{15}{2}, \frac{144}{5}\)

    Exercício\(\PageIndex{28}\) Find the Partial Sum

    Nos exercícios a seguir, expanda a soma parcial e encontre seu valor.

    1. \(\sum_{i=1}^{5} i^{2}\)
    2. \(\sum_{i=1}^{5} i^{3}\)
    3. \(\sum_{i=1}^{6}(2 i+3)\)
    4. \(\sum_{i=1}^{6}(3 i-2)\)
    5. \(\sum_{i=1}^{4} 2^{i}\)
    6. \(\sum_{i=1}^{4} 3^{i}\)
    7. \(\sum_{k=0}^{3} \frac{4}{k !}\)
    8. \(\sum_{k=0}^{4}-\frac{1}{k !}\)
    9. \(\sum_{k=1}^{5} k(k+1)\)
    10. \(\sum_{k=1}^{5} k(2 k-3)\)
    11. \(\sum_{n=1}^{5} \frac{n}{n+1}\)
    12. \(\sum_{n=1}^{4} \frac{n}{n+2}\)
    Responda

    1. \(1+4+9+16+25=55\)

    3. \(5+7+9+11+13+15=60\)

    5. \(2+4+8+16=30\)

    7. \(\frac{4}{1}+\frac{4}{1}+\frac{4}{2}+\frac{4}{6}+\frac{32}{3}=10 \frac{2}{3}\)

    9. \(2+6+12+20+30=70\)

    11. \(\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\frac{4}{5}+\frac{5}{6}=\frac{71}{20}\)

    Exercício\(\PageIndex{29}\) Use Summation Notation to Write a Sum

    Nos exercícios a seguir, escreva cada soma usando a notação de soma.

    1. \(\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}+\frac{1}{243}\)
    2. \(\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\frac{1}{256}\)
    3. \(1+\frac{1}{8}+\frac{1}{27}+\frac{1}{64}+\frac{1}{125}\)
    4. \(\frac{1}{5}+\frac{1}{25}+\frac{1}{125}+\frac{1}{625}\)
    5. \(2+1+\frac{2}{3}+\frac{1}{2}+\frac{2}{5}\)
    6. \(3+\frac{3}{2}+1+\frac{3}{4}+\frac{3}{5}+\frac{1}{2}\)
    7. \(3-6+9-12+15\)
    8. \(-5+10-15+20-25\)
    9. \(-2+4-6+8-10+\ldots+20\)
    10. \(1-3+5-7+9+\ldots+21\)
    11. \(14+16+18+20+22+24+26\)
    12. \(9+11+13+15+17+19+21\)
    Responda

    1. \(\sum_{n=1}^{5} \frac{1}{3^{n}}\)

    3. \(\sum_{n=1}^{5} \frac{1}{n^{3}}\)

    5. \(\sum_{n=1}^{5} \frac{2}{n}\)

    7. \(\sum_{n=1}^{5}(-1)^{n+1} 3 n\)

    9. \(\sum_{n=1}^{10}(-1)^{n} 2 n\)

    11. \(\sum_{n=1}^{7}(2 n+12)\)

    Exercício\(\PageIndex{30}\) Writing Exercises
    1. Com suas próprias palavras, explique como escrever os termos de uma sequência quando você conhece a fórmula. Mostre um exemplo para ilustrar sua explicação.
    2. Quais termos da sequência são negativos quando o\(n^{th}\) termo da sequência é\(a_{n}=(-1)^{n}(n+2)\)?
    3. Com suas próprias palavras, explique o que significa\(n!\) Mostrar alguns exemplos para ilustrar sua explicação.
    4. Explique o que\(\sum_{k=1}^{12} 2 k\) significa cada parte da notação.
    Responda

    1. As respostas podem variar.

    3. As respostas podem variar.

    Verificação automática

    a. Depois de concluir os exercícios, use esta lista de verificação para avaliar seu domínio dos objetivos desta seção.

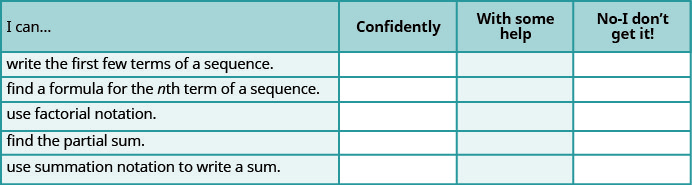
    Esta figura mostra uma tabela com quatro colunas e seis linhas. A primeira linha é a linha do cabeçalho e rotula cada coluna como “Eu posso”, “Com confiança”, “Com alguma ajuda” e “Não, eu não entendo!”. A primeira linha na segunda coluna diz: “Escreva os primeiros termos de uma sequência”, a terceira linha, primeira coluna, diz: “Encontre uma fórmula para o enésimo termo de uma sequência”, a primeira coluna da quarta linha diz “Use notação fatorial, a quinta linha, a primeira coluna diz: Encontre a soma parcial” e a última linha, primeira A coluna diz: “Use a notação de soma para escrever uma soma”. As três colunas e linhas restantes estão em branco.
    Figura 12.1.24

    b. Se a maioria dos seus cheques fosse:

    ... com confiança. Parabéns! Você alcançou os objetivos desta seção. Reflita sobre as habilidades de estudo que você usou para continuar a usá-las. O que você fez para ter certeza de sua capacidade de fazer essas coisas? Seja específico.

    ... com alguma ajuda. Isso deve ser abordado rapidamente porque tópicos que você não domina se tornam buracos em seu caminho para o sucesso. Em matemática, cada tópico se baseia em trabalhos anteriores. É importante ter certeza de que você tem uma base sólida antes de seguir em frente. A quem você pode pedir ajuda? Seus colegas de classe e instrutor são bons recursos. Há algum lugar no campus onde os professores de matemática estejam disponíveis? Suas habilidades de estudo podem ser aprimoradas?

    ... não - eu não entendo! Este é um sinal de alerta e você não deve ignorá-lo. Você deve procurar ajuda imediatamente ou ficará sobrecarregado rapidamente. Consulte seu instrutor o mais rápido possível para discutir sua situação. Juntos, vocês podem elaborar um plano para obter a ajuda de que precisam.