12.2: Sequências
- Page ID
- 183046
Ao final desta seção, você poderá:
- Escreva os primeiros termos de uma sequência
- Encontre uma fórmula para o termo geral (enésimo termo) de uma sequência
- Use notação fatorial
- Encontre a soma parcial
- Use a notação de soma para escrever uma soma
Antes de começar, faça este teste de prontidão.
- Avalie\(2n+3\) os números inteiros\(1, 2, 3\),\(4\) e.
Se você perdeu esse problema, revise o Exemplo 1.6. - Avalie\((−1)^{n}\) os números inteiros\(1, 2, 3\),\(4\) e.
Se você perdeu esse problema, revise o Exemplo 1.19. - Se\(f(n)=n^{2}+2\), encontre\(f(1)+f(2)+f(3)\).
Se você perdeu esse problema, revise o Exemplo 3.49.
Escreva os primeiros termos de uma sequência
Vamos examinar a função\(f(x)=2x\) e avaliá-la apenas para os números de contagem.
| \(f(x)=2x\) | |
| \(x\) | \(2x\) |
| \(1\) | \(2\) |
| \(2\) | \(4\) |
| \(3\) | \(6\) |
| \(4\) | \(8\) |
| \(5\) | \(10\) |
| \(...\) | \(...\) |
Se listarmos os valores da função em ordem como\(2, 4, 6, 8\)\(10\), e,... temos uma sequência. Uma sequência é uma função cujo domínio é a contagem de números.
Uma sequência é uma função cujo domínio é a contagem de números.
Uma sequência também pode ser vista como uma lista ordenada de números e cada número na lista é um termo. Uma sequência pode ter um número infinito de termos ou um número finito de termos. Nossa sequência tem três pontos (reticências) no final, o que indica que a lista nunca termina. Se o domínio for o conjunto de todos os números contados, a sequência será uma sequência infinita. Seu domínio é todo contando números e há um número infinito de números contando.
\(2,4,6,8,10, \dots\)
Se limitarmos o domínio a um número finito de números contados, a sequência será uma sequência finita. Se usarmos apenas os primeiros quatro números contados,\(1, 2, 3, 4\) nossa sequência seria a sequência finita,
\(2,4,6,8\)
Muitas vezes, ao trabalhar com sequências, não queremos escrever todos os termos. Queremos uma forma mais compacta de mostrar como cada termo é definido. Quando trabalhamos com funções, escrevemos\(f(x)=2x\) e dissemos que a expressão\(2x\) era a regra que definia os valores no intervalo. Embora uma sequência seja uma função, não usamos a notação de função usual. Em vez de escrever a função como\(f(x)=2x\), nós a escreveríamos como\(a_{n}=2n\). O\(a_{n}\) é o\(n\) décimo termo da sequência, o termo na posição\(n\) enésima onde\(n\) é um valor no domínio. A fórmula para escrever o\(n\) décimo termo da sequência é chamada de termo geral ou fórmula da sequência.
O termo geral da sequência é encontrado na fórmula para escrever o\(n\) décimo termo da sequência. O\(n\) décimo termo da sequência,\(a_{n}\), é o termo na posição\(n\) enésima em que\(n\) é um valor no domínio.
Quando recebemos o termo geral da sequência, podemos encontrar os termos\(n\) substituindo-os pelos números de contagem em ordem. Para\(a_{n}=2 n\),
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(a_{n}\) | 2\(\cdot 1\) | 2\(\cdot 2\) | 2\(\cdot 3\) | 2\(\cdot 4\) | 2\(\cdot 5\) | 2\(\cdot 6\) |
| \(2\) | \(4\) | \(6\) | \(8\) | \(10\) |
\(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \ldots, \quad a_{n}, \dots\)
\(2, \quad 4, \quad 6, \quad 8, \quad10, \dots\)
Para encontrar os valores de uma sequência, substituímos os números de contagem pelo termo geral da sequência.
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=4 n-3\).
Solução:
Substituímos os valores e\(1, 2, 3, 4\),\(5\) na fórmula\(a_{n}=4n−3\), em ordem.
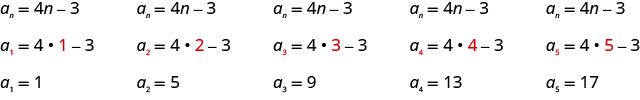
Resposta:
Os primeiros cinco termos da sequência são\(1, 5, 9, 13\),\(17\) e.
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=3n-4\).
- Resposta
-
\(-1,2,5,8,11\)
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=2n-5\).
- Resposta
-
\(-3,-1,1,3,5\)
Para algumas sequências, a variável é um expoente.
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=2^{n}+1\).
Solução:
Substituímos os valores e\(1, 2, 3, 4\),\(5\) na fórmula\(a_{n}=2^{n}+1\), em ordem.
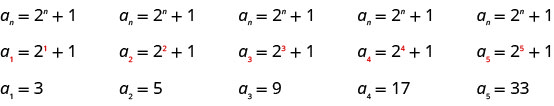
Resposta:
Os primeiros cinco termos da sequência são\(3, 5, 9, 17\),\(33\) e.
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=3^{n}+4\).
- Resposta
-
\(7,13,31,85,247\)
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=2^{n}-5\).
- Resposta
-
\(-3,-1,3,11,27\)
Não é incomum ver as expressões\((−1)^{n}\) ou\((−1)^{n+1}\) o termo geral de uma sequência. Se avaliarmos cada uma dessas expressões para alguns valores, veremos que essa expressão alterna o sinal dos termos.
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|
| \ (n\) ">\((-1)^{n}\) | \ (1\) ">\((-1)^{1}\) \(-1\) |
\ (2\) ">\((-1)^{2}\) 1 |
\ (3\) ">\((-1)^{3}\) \(-1\) |
\ (4\) ">\((-1)^{4}\) \(1\) |
\ (5\) ">\((-1)^{5}\) \(-1\) |
| \ (n\) ">\((-1)^{n+1}\) | \ (1\) ">\((-1)^{1+1}\) 1 |
\ (2\) ">\((-1)^{2+1}\) \(-1\) |
\ (3\) ">\((-1)^{3+1}\) 1 |
\ (4\) ">\((-1)^{4+1}\) \(-1\) |
\ (5\) ">\((-1)^{5+1}\) 1 |
\(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \dots, \quad a_{n}, \dots\)
\(\begin{array}{rrrr}{-1,} & {1,} & {-1,} & {1,} & {-1 \ldots} \\ {1,} & {-1,} & {1,} & {-1,} & {1 \ldots}\end{array}\)
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=(-1)^{n} n^{3}\).
Solução:
Substituímos os valores e\(1, 2, 3, 4\),\(5\) na fórmula\(a_{n}=(-1)^{n} n^{3}\), em ordem.
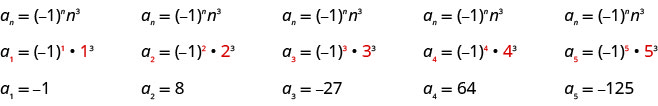
Resposta:
Os primeiros cinco termos da sequência são\(−1, 8, −27, 64, −1, 8, −27, 64\),\(−125\) e.
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=(-1)^{n} n^{2}\).
- Resposta
-
\(-1,4,-9,16,-25\)
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=(-1)^{n+1} n^{3}\).
- Resposta
-
\(1,-8,27,-64,125\)
Encontre uma fórmula para o termo geral (\(n\)ésimo termo) de uma sequência
Às vezes, temos alguns termos de uma sequência e seria útil conhecer o termo geral ou\(n\) o termo. Para encontrar o termo geral, procuramos padrões nos termos. Muitas vezes, os padrões envolvem múltiplos ou poderes. Também procuramos um padrão nos sinais dos termos.
Encontre um termo geral para a sequência cujos primeiros cinco termos são mostrados. \(4,8,12,16,20, \dots\)
Solução:
-


Procuramos um padrão nos termos. 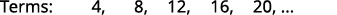
Os números são todos múltiplos de\(4\). 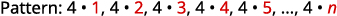
O termo geral da sequência é\(a_{n}=4n\). Tabela 12.1.4 Resposta:
O termo geral da sequência é\(a_{n}=4n\).
Encontre um termo geral para a sequência cujos primeiros cinco termos são mostrados.
\(3,6,9,12,15, \dots\)
- Resposta
-
\(a_{n}=3 n\)
Encontre um termo geral para a sequência cujos primeiros cinco termos são mostrados.
\(5,10,15,20,25, \dots\)
- Responda
-
\(a_{n}=5 n\)
Encontre um termo geral para a sequência cujos primeiros cinco termos são mostrados. \(2,-4,8,-16,32, \dots\)
Solução:
-
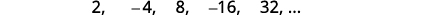
Figura 12.1.8 
Figura 12.1.9 Procuramos um padrão nos termos. 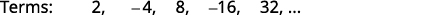
Figura 12.1.10 Os números são potências de\(2\). Os sinais são alternados, com até mesmo\(n\) negativos. 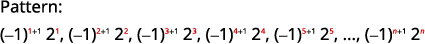
Figura 12.1.11 O termo geral da sequência é\(a_{n}=(-1)^{n+1} 2^{n}\) Tabela 12.1.5 Resposta:
O termo geral da sequência é\(a_{n}=(-1)^{n+1}2^{n}\).
Encontre um termo geral para a sequência cujos primeiros cinco termos são mostrados.
\(-3,9,-27,81,-243, \dots\)
- Responda
-
\(a_{n}=(-1)^{n} 3^{n}\)
Encontre um termo geral para a sequência cujos primeiros cinco termos são mostrados
\(1,-4,9,-16,25, \dots\)
- Responda
-
\(a_{n}=(-1)^{n+1} n^{2}\)
Encontre um termo geral para a sequência cujos primeiros cinco termos são mostrados. \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \frac{1}{243}, \dots\)
Solução:
-
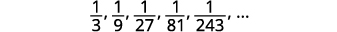
Figura 12.1.12 
Figura 12.1.13 Procuramos um padrão nos termos. 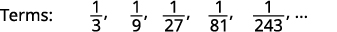
Figura 12.1.14 Os numeradores são todos\(1\). 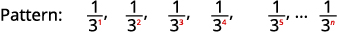
Figura 12.1.15 Os denominadores são poderes de\(3\). O termo geral da sequência é\(a_{n}=\frac{1}{3^{n}}\). Tabela 12.1.6 Resposta:
O termo geral da sequência é\(a_{n}=\frac{1}{3^{n}}\).
Encontre um termo geral para a sequência cujos primeiros cinco termos são mostrados.
\(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \dots\)
- Responda
-
\(a_{n}=\frac{1}{2^{n}}\)
Encontre um termo geral para a sequência cujos primeiros cinco termos são mostrados.
\(\frac{1}{1}, \frac{1}{4}, \frac{1}{9}, \frac{1}{16}, \frac{1}{25}, \dots\)
- Responda
-
\(a_{n}=\frac{1}{n^{2}}\)
Use notação fatorial
As sequências geralmente têm termos que são produtos de números inteiros consecutivos. Indicamos esses produtos com uma notação especial chamada notação fatorial. Por exemplo\(5!\), leia\(5\) fatorial, significa\(5⋅4⋅3⋅2⋅1\). O ponto de exclamação não é pontuação aqui; ele indica a notação fatorial.
Se\(n\) for um número inteiro positivo, então\(n!\) é
\(n !=n(n-1)(n-2) \dots\)
Nós definimos\(0!\) como\(1\), então\(0!=1\).
Os valores de\(n!\) para os primeiros números inteiros\(5\) positivos são mostrados.
\(\begin{array}{ccccc}{1 !} & {2 !} & {3 !} & {4 !} & {5 !} \\ {1} & \quad{2 \cdot 1} & \quad {3 \cdot 2 \cdot 1} & \quad{4 \cdot 3 \cdot 2 \cdot 1} & \quad {5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ {1} & {2} & {6} & {24} & {120}\end{array}\)
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=\frac{1}{n !}\).
Solução:
Substituímos os valores\(1, 2, 3, 4, 5\) na fórmula,\(a_{n}=\frac{1}{n !}\), em ordem.
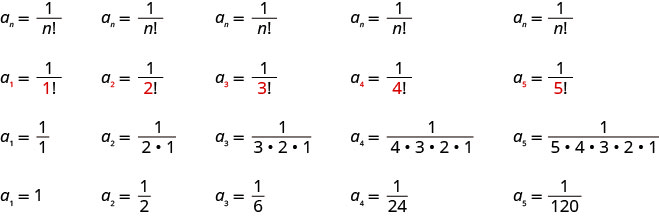
Resposta:
Os primeiros cinco termos da sequência são\(1, \frac{1}{2}, \frac{1}{6}, \frac{1}{24}, \frac{1}{120}\).
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=\frac{2}{n !}\).
- Responda
-
\(2,1, \frac{1}{3}, \frac{1}{12}, \frac{1}{60}\)
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=\frac{3}{n !}\).
- Responda
-
\(3, \frac{3}{2}, \frac{1}{2}, \frac{1}{8}, \frac{1}{40}\)
Quando há uma fração com fatoriais no numerador e no denominador, alinhamos os fatores verticalmente para facilitar nossos cálculos.
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=\frac{(n+1) !}{(n-1) !}\).
Solução:
Substituímos os valores\(1, 2, 3, 4, 5\) na fórmula,\(a_{n}=\frac{(n+1) !}{(n-1) !}\), em ordem.
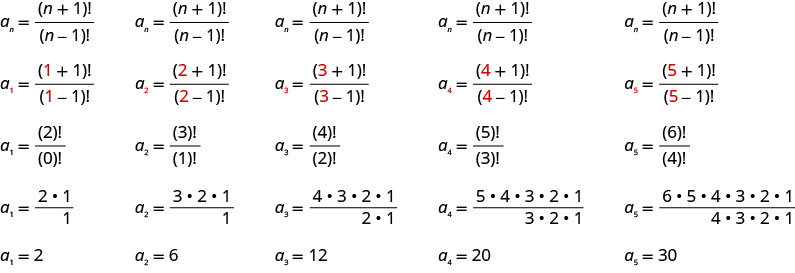
Resposta:
Os primeiros cinco termos da sequência são\(2, 6, 12, 20\),\(30\) e.
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=\frac{(n-1) !}{(n+1) !}\)
- Responda
-
\(\frac{1}{2}, \frac{1}{6}, \frac{1}{12}, \frac{1}{20}, \frac{1}{30}\)
Escreva os primeiros cinco termos da sequência cujo termo geral é\(a_{n}=\frac{n !}{(n+1) !}\).
- Responda
-
\(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}\)
Encontre a soma parcial
Às vezes, em aplicativos, em vez de apenas listar os termos, é importante adicionarmos os termos de uma sequência. Em vez de apenas conectar os termos com sinais de adição, podemos usar a notação de soma.
Por exemplo,\(a_{1}+a_{2}+a_{3}+a_{4}+a_{5}\) pode ser escrito como\(\sum_{i=1}^{5} a_{i}\). Lemos isso como “a soma de\(a\) sub\(i\) de\(i\) é igual a um a cinco”. O símbolo\(∑\) significa somar e o\(i\) é o índice da soma. O nos\(1\) diz por onde começar (valor inicial) e o nos\(5\) diz onde terminar (valor terminal).
A soma dos primeiros\(n\) termos de uma sequência cujo\(n\) décimo termo é\(a_{n}\) é escrita em notação de soma como:
\(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)
O\(i\) é o índice da soma e o nos\(1\) diz por onde começar e por onde terminar.\(n\)
Quando adicionamos um número finito de termos, chamamos a soma de soma parcial.
Expanda a soma parcial e encontre seu valor:\(\sum_{i=1}^{5} 2 i\).
Solução:
-
\(\sum_{i=1}^{5} 2 i\) Substituímos os valores\(1, 2, 3, 4, 5\) em ordem. \(2 \cdot 1+2 \cdot 2+2 \cdot 3+2 \cdot 4 + 2 \cdot 5\) Simplifique. \(2+4+6+8+10\) Adicionar. \(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\) Tabela 12.1.7 Resposta:
\(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\)
Expanda a soma parcial e encontre seu valor:\(\sum_{i=1}^{5} 3 i\).
- Responda
-
\(45\)
Expanda a soma parcial e encontre seu valor:\(\sum_{i=1}^{5} 4 i\).
- Responda
-
\(60\)
O índice nem sempre precisa ser:\(i\) podemos usar qualquer letra, mas sim\(i\) e\(k\) somos comumente usados. O índice não precisa começar com nenhum dos\(1\) dois — ele pode começar e terminar com qualquer número inteiro positivo.
Expanda a soma parcial e encontre seu valor:\(\sum_{k=0}^{3} \frac{1}{k !}\).
Solução:
\(\begin{array}{c c} {}&{\sum_{k=0}^{3} \frac{1}{k !}} \\ {We\:substitute\:the\:values\:0,1,2,3\:in\:order.}&{\frac{1}{1}+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}} \\ {Evaluate\:the\:factorials.}& {\frac{1}{1}+\frac{1}{1}+\frac{1}{2 !}+\frac{1}{6}} \\ {Simplify.}&{1+1+\frac{3}{6}+\frac{1}{6}} \\{Simplify.}& {\frac{16}{6}} \\ {Simplify.}&{\frac{8}{3}} \\{}& {\sum_{k=0}^{3} \frac{1}{k !}=\frac{8}{3}}\end{array}\)
Expanda a soma parcial e encontre seu valor:\(\sum_{k=0}^{3} \frac{2}{k !}\).
- Responda
-
\(\frac{16}{3}\)
Expanda a soma parcial e encontre seu valor:\(\sum_{k=0}^{3} \frac{3}{k !}\).
- Responda
-
\(8\)
Use a notação de soma para escrever uma soma
Nos dois últimos exemplos, passamos da notação somatória para a escrita da soma. Agora vamos começar com uma soma e alterá-la para notação de soma. Isso é muito parecido com encontrar o termo geral de uma sequência. Precisaremos examinar os termos e encontrar um padrão. Muitas vezes, os padrões envolvem múltiplos ou poderes.
Escreva a soma usando a notação somatória:\(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\).
Solução:
\(\begin{array} {}&{ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}} \\ {}&{n : 1,2,3,4,5} \\ {\text{We look for a pattern in the terms.}}&{\text { Terms: } 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}} \\ {\text{The numerators are all one.}}&{\text { Pattern: } \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots \frac{1}{n}} \\ {\text{The denominators are the counting numbers from one to five.}}&{\text{The sum written in summation notation}} \\ {}&{1 + \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}=\sum^{5}_{n=1} \frac{1}{n}.} \end{array}\)
Escreva a soma usando a notação somatória:\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\).
- Responda
-
\(\sum_{n=1}^{5} \frac{1}{2^{n}}\)
Escreva a soma usando a notação de soma:\(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}\)
- Responda
-
\(\sum_{n=1}^{5} \frac{1}{n^{2}}\)
Quando os termos de uma soma têm coeficientes negativos, devemos analisar cuidadosamente o padrão dos sinais.
Escreva a soma usando a notação somatória:\(-1+8-27+64-125\).
Solução:
-
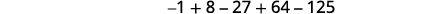
Figura 12.1.18 
Figura 12.1.19 Procuramos um padrão nos termos. 
Figura 12.1.20 Os sinais dos termos se alternam
e os termos ímpares são negativos.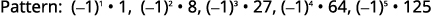
Figura 12.1.21 Os números são os cubos dos números
contados de um a cinco.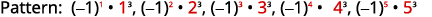
Figura 12.1.22 
Figura 12.1.23 A soma escrita em notação de soma é \(-1+8-27+64-125=\sum_{n=1}^{5}(-1)^{n} \cdot n^{3}\) Tabela 12.1.8
Escreva cada soma usando a notação somatória:\(1-4+9-16+25\).
- Responda
-
\(\sum_{n=1}^{5}(-1)^{n+1} n^{2}\)
Escreva cada soma usando a notação somatória:\(-2+4-6+8-10\).
- Responda
-
\(\sum_{n=1}^{5}(-1)^{n} 2 n\)
Acesse este recurso on-line para obter instruções e práticas adicionais com sequências.
Conceitos-chave
- Notação fatorial
Se\(n\) for um número inteiro positivo, então\(n!\) é
\(n !=n(n-1)(n-2) \ldots(3)(2)(1)\)
Nós definimos\(0!\) como\(1\), então\(0!=1\)
- Notação de soma
A soma dos primeiros\(n\) termos de uma sequência cujo\(n\) décimo termo\(a_{n}\) está escrito em notação de soma como:
\(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)
O\(i\) é o índice da soma e o nos\(1\) diz por onde começar e por onde terminar.\(n\)
Glossário
- sequência finita
- Uma sequência com um domínio limitado a um número finito de números contados.
- termo geral de uma sequência
- O termo geral da sequência é a fórmula para escrever o\(n\) décimo termo da sequência. O\(n\) décimo termo da sequência,\(a_{n}\), é o termo na posição\(n\) enésima em que\(n\) é um valor no domínio.
- sequência infinita
- Uma sequência cujo domínio é toda contagem de números e há um número infinito de números contando.
- soma parcial
- Quando adicionamos um número finito de termos de uma sequência, chamamos a soma de soma parcial.
- sequência
- Uma sequência é uma função cujo domínio é a contagem de números.


