Skip to main content
Global

11.6E: Exercícios

  1. Last updated
  2. Save as PDF
  • Page ID
    183710

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    A prática leva à perfeição

    Exercício\(\PageIndex{17}\) Solve a System of Nonlinear Equations Using Graphing

    Nos exercícios a seguir, resolva o sistema de equações usando gráficos.

    1. \(\left\{\begin{array}{l}{y=2 x+2} \\ {y=-x^{2}+2}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{y=6 x-4} \\ {y=2 x^{2}}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{x+y=2} \\ {x=y^{2}}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x-y=-2} \\ {x=y^{2}}\end{array}\right.\)
    5. \(\left\{\begin{array}{l}{y=\frac{3}{2} x+3} \\ {y=-x^{2}+2}\end{array}\right.\)
    6. \(\left\{\begin{array}{l}{y=x-1} \\ {y=x^{2}+1}\end{array}\right.\)
    7. \(\left\{\begin{array}{l}{x=-2} \\ {x^{2}+y^{2}=4}\end{array}\right.\)
    8. \(\left\{\begin{array}{l}{y=-4} \\ {x^{2}+y^{2}=16}\end{array}\right.\)
    9. \(\left\{\begin{array}{l}{x=2} \\ {(x+2)^{2}+(y+3)^{2}=16}\end{array}\right.\)
    10. \(\left\{\begin{array}{l}{y=-1} \\ {(x-2)^{2}+(y-4)^{2}=25}\end{array}\right.\)
    11. \(\left\{\begin{array}{l}{y=-2 x+4} \\ {y=\sqrt{x}+1}\end{array}\right.\)
    12. \(\left\{\begin{array}{l}{y=-\frac{1}{2} x+2} \\ {y=\sqrt{x}-2}\end{array}\right.\)
    Responda

    2.

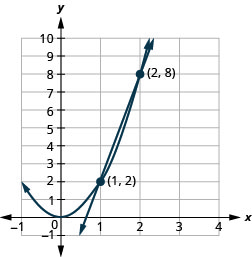
    Este gráfico mostra as equações de um sistema, y é igual a 6 x menos 4 que é uma linha e y é igual a 2 x ao quadrado que é uma parábola, no plano de coordenadas x y. O vértice da parábola é (0, 0) e a parábola se abre para cima. A linha tem uma inclinação de 6. A linha e a parábola se cruzam nos pontos (1, 2) e (2, 8), que são rotulados. As soluções são (1, 2) e (2, 8).
    Figura 11.5.61

    4.

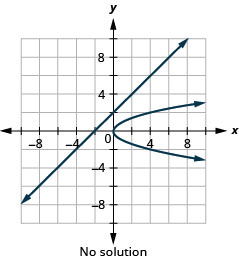
    Este gráfico mostra as equações de um sistema, x menos y é igual a menos 2 que é uma linha e x é igual a y ao quadrado, que é uma parábola de abertura para a direita, no plano de coordenadas x y. O vértice da parábola é (0, 0) e passa pelos pontos (1, 1) e (1, menos 1). A linha tem uma inclinação de 1 e um intercepto y em 2. A linha e a parábola não se cruzam, então o sistema não tem solução.
    Figura 11.5.62

    6.

    Este gráfico mostra as equações de um sistema, y é x menos 1 que é uma linha e y é igual a x ao quadrado mais 1 que é uma parábola de abertura ascendente, no plano de coordenadas x y. O vértice da parábola é (0, 1) e passa pelos pontos (menos 1, 2) e (1, 2). A linha tem uma inclinação de 1 e um intercepto y em menos 1. A linha e a parábola não se cruzam, então o sistema não tem solução.
    Figura 11.5.63

    8.

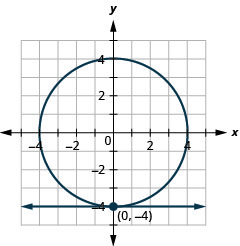
    Este gráfico mostra as equações de um sistema, x é igual a menos 2 que é uma linha e x ao quadrado mais y ao quadrado é igual a 16 que é um círculo, no plano de coordenadas x y. A linha é horizontal. O centro do círculo é (0, 0) e o raio do círculo é 4. A linha e o círculo se cruzam em (menos 2, 0), então a solução do sistema é (menos 2, 0).
    Figura 11.5.64

    10.

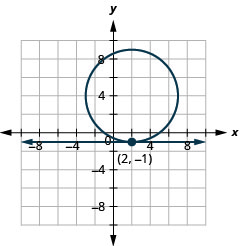
    Este gráfico mostra as equações de um sistema, x é igual a 2 que é uma linha e a quantidade x menos 2 quantidade final ao quadrado mais a quantidade y menos 4 quantidade final ao quadrado é igual a 25, que é um círculo, no plano de coordenadas x y. A linha é horizontal. O centro do círculo é (2, 4) e o raio do círculo é 5. A linha e o círculo se cruzam em (2, menos 1), então a solução do sistema é (2, menos 1).
    Figura 11.5.65

    12.

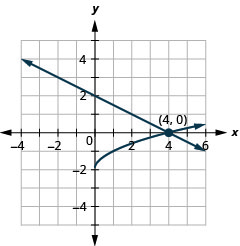
    Este gráfico mostra as equações de um sistema, y é igual a menos meio x mais 2 que é uma linha e y é igual à raiz quadrada de x menos 2, no plano de coordenadas x y. A curva para y é igual à raiz quadrada de x menos 2 A curva para y é igual à raiz quadrada de x mais 1, onde x é maior ou igual a 0 e y é maior ou igual a menos 2. A linha e a curva da raiz quadrada se cruzam em (4, 0), então a solução é (4, 0).
    Figura 11.5.66
    Exercício\(\PageIndex{18}\) Solve a System of Nonlinear Equations Using Substitution

    Nos exercícios a seguir, resolva o sistema de equações usando a substituição.

    1. \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {y=\frac{1}{2} x-1}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x+3}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=x+3}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {x=2}\end{array}\right.\)
    5. \(\left\{\begin{array}{l}{4 x^{2}+y^{2}=4} \\ {y=4}\end{array}\right.\)
    6. \(\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.\)
    7. \(\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.\)
    8. \(\left\{\begin{array}{l}{2 y^{2}-x=0} \\ {y=x+1}\end{array}\right.\)
    9. \(\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=x+3}\end{array}\right.\)
    10. \(\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.\)
    11. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {x-y=1}\end{array}\right.\)
    12. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {2 x+y=10}\end{array}\right.\)
    Responda

    2. \((-1,0),(0,3)\)

    4. \((2,0)\)

    6. \((12,-5),(12,5)\)

    8. Sem solução

    10. \((0,-4),(1,-3)\)

    12. \((3,4),(5,0)\)

    Exercício\(\PageIndex{19}\) Solve a System of Nonlinear Equations Using Elimination

    Nos exercícios a seguir, resolva o sistema de equações usando a eliminação.

    1. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y=8}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-y=4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}+2 y=1}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y=2}\end{array}\right.\)
    5. \(\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=3}\end{array}\right.\)
    6. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {y^{2}-x=2}\end{array}\right.\)
    7. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {2 x^{2}-3 y^{2}=5}\end{array}\right.\)
    8. \(\left\{\begin{array}{l}{x^{2}+y^{2}=20} \\ {x^{2}-y^{2}=-12}\end{array}\right.\)
    9. \(\left\{\begin{array}{l}{x^{2}+y^{2}=13} \\ {x^{2}-y^{2}=5}\end{array}\right.\)
    10. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-y^{2}=16}\end{array}\right.\)
    11. \(\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.\)
    12. \(\left\{\begin{array}{l}{x^{2}-y^{2}=3} \\ {2 x^{2}+y^{2}=6}\end{array}\right.\)
    13. \(\left\{\begin{array}{l}{4 x^{2}-y^{2}=4} \\ {4 x^{2}+y^{2}=4}\end{array}\right.\)
    14. \(\left\{\begin{array}{l}{x^{2}-y^{2}=-5} \\ {3 x^{2}+2 y^{2}=30}\end{array}\right.\)
    15. \(\left\{\begin{array}{l}{x^{2}-y^{2}=1} \\ {x^{2}-2 y=4}\end{array}\right.\)
    16. \(\left\{\begin{array}{l}{2 x^{2}+y^{2}=11} \\ {x^{2}+3 y^{2}=28}\end{array}\right.\)
    Responda

    2. \((0,-4),(-\sqrt{7}, 3),(\sqrt{7}, 3)\)

    4. \((0,-2),(-\sqrt{3}, 1),(\sqrt{3}, 1)\)

    6. \((-2,0),(1,-\sqrt{3}),(1, \sqrt{3})\)

    8. \((-2,-4),(-2,4),(2,-4),(2,4)\)

    10. \((-4,0),(4,0)\)

    12. \((-\sqrt{3}, 0),(\sqrt{3}, 0)\)

    14. \((-2,-3),(-2,3),(2,-3),(2,3)\)

    16. \((-1,-3),(-1,3),(1,-3),(1,3)\)

    Exercício\(\PageIndex{20}\) Use a System of Nonlinear Equations to Solve Applications

    Nos exercícios a seguir, resolva o problema usando um sistema de equações.

    1. A soma de dois números é\(−6\) e o produto é\(8\). Encontre os números.
    2. A soma de dois números é\(11\) e o produto é\(−42\). Encontre os números.
    3. A soma dos quadrados de dois números é\(65\). A diferença do número é\(3\). Encontre os números.
    4. A soma dos quadrados de dois números é\(113\). A diferença do número é\(1\). Encontre os números.
    5. A diferença dos quadrados de dois números é\(15\). A diferença de duas vezes o quadrado do primeiro número e o quadrado do segundo número é\(30\). Encontre os números.
    6. A diferença dos quadrados de dois números é\(20\). A diferença entre o quadrado do primeiro número e o dobro do quadrado do segundo número é\(4\). Encontre os números.
    7. O perímetro de um retângulo é\(32\) polegadas e sua área é polegadas\(63\) quadradas. Encontre o comprimento e a largura do retângulo.
    8. O perímetro de um retângulo é\(52\) cm e sua área é\(165\)\(\mathrm{cm}^{2}\). Encontre o comprimento e a largura do retângulo.
    9. Dion comprou um novo microondas. A diagonal da porta mede\(17\) polegadas. A porta também tem uma área de polegadas\(120\) quadradas. Quais são o comprimento e a largura da porta do micro-ondas?
    10. Jules comprou um micro-ondas para sua cozinha. A diagonal da frente do micro-ondas mede\(26\) polegadas. A frente também tem uma área de polegadas\(240\) quadradas. Quais são o comprimento e a largura do micro-ondas?
    11. Roman encontrou uma TV widescreen à venda, mas não tem certeza se ela caberá em seu centro de entretenimento. A TV é\(60\)”. O tamanho de uma TV é medido na diagonal da tela e uma tela widescreen tem um comprimento maior que a largura. A tela também tem uma área de polegadas\(1728\) quadradas. Seu centro de entretenimento tem um encaixe para a TV com um comprimento de\(50\) polegadas e largura de\(40\) polegadas. Quais são o comprimento e a largura da tela da TV e ela se encaixa no centro de entretenimento de Roman?
    12. Donnette encontrou uma TV widescreen em uma venda de garagem, mas não tem certeza se ela caberá em seu centro de entretenimento. A TV é\(50\)”. O tamanho de uma TV é medido na diagonal da tela e uma tela widescreen tem um comprimento maior que a largura. A tela também tem uma área de polegadas\(1200\) quadradas. Seu centro de entretenimento tem um encaixe para a TV com um comprimento de\(38\) polegadas e largura de\(27\) polegadas. Quais são o comprimento e a largura da tela da TV e ela caberá no centro de entretenimento de Donnette?
    Responda

    2. \(-3\)e\(14\)

    4. \(-7\)e\(-8\) ou\(8\) e\(7\)

    6. \(-6\)e\(-4\) ou\(-6\) e\(4\) ou\(6\) e\(-4\) ou\(6\) e\(4\)

    8. Se o comprimento for\(11\) cm, a largura será\(15\) cm. Se o comprimento for\(15\) cm, a largura será\(11\) cm.

    10. Se o comprimento for\(10\) polegadas, a largura será\(24\) polegadas. Se o comprimento for\(24\) polegadas, a largura será\(10\) polegadas.

    12. O comprimento é\(40\) polegadas e a largura é\(30\) polegadas. A TV não cabe no centro de entretenimento de Donnette.

    Exercício\(\PageIndex{21}\) Writing Exercises
    1. Com suas próprias palavras, explique as vantagens e desvantagens de resolver um sistema de equações por meio de gráficos.
    2. Explique com suas próprias palavras como resolver um sistema de equações usando a substituição.
    3. Explique com suas próprias palavras como resolver um sistema de equações usando a eliminação.
    4. Um círculo e uma parábola podem se cruzar de maneiras que resultariam em\(4\) soluções\(0, 1, 2, 3,\) ou soluções. Desenhe um esboço de cada uma das possibilidades.
    Responda

    2. As respostas podem variar

    4. As respostas podem variar

    Verificação automática

    a. Depois de concluir os exercícios, use esta lista de verificação para avaliar seu domínio dos objetivos desta seção.

    Essa tabela tem quatro colunas e cinco linhas. A primeira linha é um cabeçalho e rotula cada coluna, “Eu não posso”, “Confiantemente”, “Com alguma ajuda, †— e “não, eu não entendo!™ †Na linha 2, o I can foi resolver um sistema de equações não lineares usando gráficos. Na linha 3, o I pode resolver um sistema de equações não lineares usando substituição. Na linha 4, o I can foi resolver um sistema de equações não lineares usando a eliminação. Na linha 5, o I can era usar um sistema de equações não lineares para resolver aplicações.
    Figura 11.5.67

    b. Depois de examinar a lista de verificação, você acha que está bem preparado para a próxima seção? Por que ou por que não?