Home
Idioma Portugues
Álgebra intermediária (OpenStax)
11: Cônicas
11.6: Resolvendo sistemas de equações não lineares

11.6: Resolvendo sistemas de equações não lineares

Last updated
Save as PDF

Page ID: 183701

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Ao final desta seção, você poderá:

Resolva um sistema de equações não lineares usando gráficos
Resolva um sistema de equações não lineares usando substituição
Resolva um sistema de equações não lineares usando eliminação
Use um sistema de equações não lineares para resolver aplicações

Antes de começar, faça este teste de prontidão.

Resolva o sistema representando graficamente:$\left\{\begin{array}{l}{x-3 y=-3} \\ {x+y=5}\end{array}\right.$.
Se você perdeu esse problema, consulte o Exemplo 4.2.
Resolva o sistema por substituição:$\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.$
Se você perdeu esse problema, consulte o Exemplo 4.7.
Resolva o sistema eliminando:$\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right.$
Se você perdeu esse problema, consulte o Exemplo 4.9.

Resolva um sistema de equações não lineares usando gráficos

Aprendemos como resolver sistemas de equações lineares com duas variáveis por meio de representação gráfica, substituição e eliminação. Usaremos esses mesmos métodos ao examinarmos sistemas de equações não lineares com duas equações e duas variáveis. Um sistema de equações não lineares é um sistema em que pelo menos uma das equações não é linear.

Por exemplo, cada um dos sistemas a seguir é um sistema de equações não lineares.

$\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=9}\end{array}\right. \left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x-3}\end{array}\right. \left\{\begin{array}{l}{x+y=4} \\ {y=x^{2}+2}\end{array}\right.$

Definição$\PageIndex{1}$

Um sistema de equações não lineares é um sistema em que pelo menos uma das equações não é linear.

Assim como com sistemas de equações lineares, uma solução de um sistema não linear é um par ordenado que torna ambas as equações verdadeiras. Em um sistema não linear, pode haver mais de uma solução. Veremos isso ao resolvermos um sistema de equações não lineares por meio de gráficos.

Quando resolvemos sistemas de equações lineares, a solução do sistema foi o ponto de interseção das duas retas. Com sistemas de equações não lineares, os gráficos podem ser círculos, parábolas ou hipérboles e pode haver vários pontos de interseção e, portanto, várias soluções. Depois de identificar os gráficos, visualize as diferentes maneiras pelas quais os gráficos podem se cruzar e, portanto, quantas soluções podem existir.

Para resolver sistemas de equações não lineares por meio de gráficos, usamos basicamente as mesmas etapas dos sistemas de equações lineares modificados ligeiramente para equações não lineares. As etapas estão listadas abaixo para referência.

Resolva um sistema de equações não lineares representando graficamente.

Identifique o gráfico de cada equação. Esboce as opções possíveis para a interseção.
Faça um gráfico da primeira equação.
Faça um gráfico da segunda equação no mesmo sistema de coordenadas retangulares.
Determine se os gráficos se cruzam.
Identifique os pontos de interseção.
Verifique se cada par ordenado é uma solução para ambas as equações originais.

Exemplo$\PageIndex{1}$

Resolva o sistema representando graficamente:$\left\{\begin{array}{l}{x-y=-2} \\ {y=x^{2}}\end{array}\right.$

Solução:

Tabela 11.5.1
Identifique cada gráfico.	$\left\{\begin{array}{ll}{x-y=-2} & {\text { line }} \\ {y=x^{2}} & {\text { parabola }}\end{array}\right.$
Esboce as opções possíveis para a interseção de uma parábola e uma linha.	$.$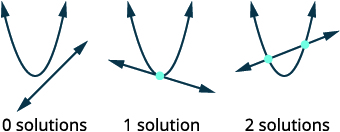
Faça um gráfico da linha,$x-y=-2$. Forma de interceptação de inclinação$y=x+2$. Faça um gráfico da parábola,$y=x^{2}$.	$.$
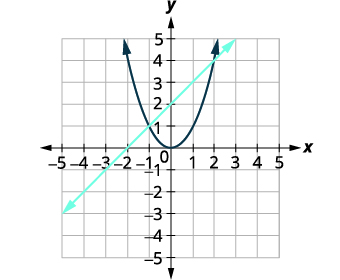Identifique os pontos de interseção.	Os pontos de interseção parecem ser$(2,3)$$(-1,1)$ e.
Verifique se cada solução torna as duas equações verdadeiras. $(2,4)$ $\begin{array} {r l } {x-y=-2}\quad\quad {y=x^{2}} \\ {2-4\stackrel{?}{=}-2}\quad\quad {4\stackrel{?}{=}2^{2}} \\ {-2 = -2}\quad\quad\:{4 = 4} \end{array}$ $(-1,1)$ $\begin{array} {l l } {x-y=-2}\quad\quad {y=x^{2}} \\ {-1-1\stackrel{?}{=}-2}\:\quad {1\stackrel{?}{=}(-1)^{2}} \\ {-2 = -2}\quad\quad\quad{1 = 1} \end{array}$
	As soluções são$(2,4)$$(-1,1)$ e.

Exercício$\PageIndex{1}$

Resolva o sistema representando graficamente:$\left\{\begin{array}{l}{x+y=4} \\ {y=x^{2}+2}\end{array}\right.$.

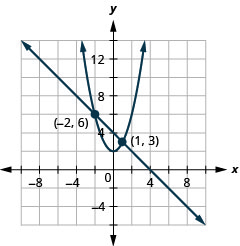
Responda: $Este gráfico mostra as equações de um sistema, x mais y é igual a 4 e y é igual a x ao quadrado mais 2, e o plano de coordenadas x y. A linha tem uma inclinação de menos 1 e um intercepto y em 4. O vértice da parábola é (0, 2) e se abre para cima. A linha e a parábola se cruzam nos pontos (menos 2, 6) e (1, 3), que são rotulados.$
Figura 11.5.3

Exercício$\PageIndex{2}$

Resolva o sistema representando graficamente:$\left\{\begin{array}{l}{x-y=-1} \\ {y=-x^{2}+3}\end{array}\right.$

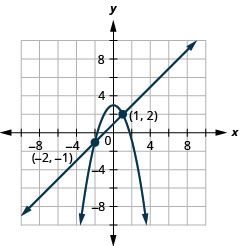
Responda: $Este gráfico mostra as equações de um sistema, x menos y é igual a menos 1 e y é igual a menos x ao quadrado mais três, e o plano de coordenadas x y. A linha tem uma inclinação de 1 e um intercepto y em 1. O vértice da parábola é (0, menos 3) e se abre para cima. A linha e a parábola se cruzam nos pontos (menos 2, menos 1) e (1, 2), que são rotulados.$
Figura 11.5.4

Para identificar o gráfico de cada equação, tenha em mente as características$x^{2}$ e os$y^{2}$ termos de cada cônica.

Exemplo$\PageIndex{2}$

Resolva o sistema representando graficamente:$\left\{\begin{array}{l}{y=-1} \\ {(x-2)^{2}+(y+3)^{2}=4}\end{array}\right.$.

Solução:

Tabela 11.5.2
Identifique cada gráfico.	$\left\{\begin{array}{ll}{y=-1} & {\text { line }} \\ {(x-2)^{2}+(y+3)^{2}=4} & {\text { circle }}\end{array}\right.$
Esboce as opções possíveis para a interseção de um círculo e uma linha.	$.$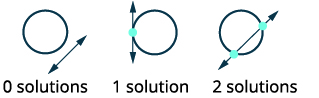
Faça um gráfico do círculo,$(x-2)^{2}+(y+3)^{2}=4$ Centro:$(2,-3)$ raio:$2$ Faça um gráfico da linha,$y=-1$. É uma linha horizontal.	$.$
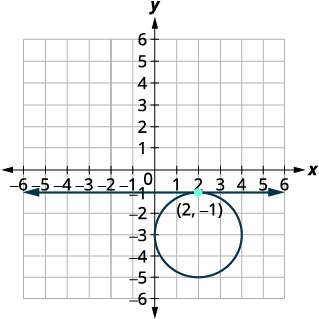Identifique os pontos de interseção.	O ponto de interseção parece ser$(2,-1)$.
Verifique se a solução torna as duas equações verdadeiras. $(2,-1)$ $\begin{array} {r r} {(x-2)^{2}+(y+3)^{2}=4} \quad\quad {y=-1} \\ {(2-2)^{2}+(-1+3)^{2}\stackrel{?}{=}4}\quad{-1=-1} \\ {(0)^{2}+(2)^{2}\stackrel{?}{=}4}\quad\quad\quad\quad\quad \\ {4=4}\quad\quad\quad\quad\quad \end{array}$
	A solução é$(2,-1)$

Exercício$\PageIndex{3}$

Resolva o sistema representando graficamente:$\left\{\begin{array}{l}{x=-6} \\ {(x+3)^{2}+(y-1)^{2}=9}\end{array}\right.$

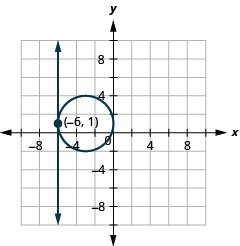
Responda: $Este gráfico mostra as equações de um sistema, x é igual a menos 6 e a quantidade x mais 3 ao quadrado mais a quantidade y menos 1 ao quadrado é igual a 9, que é um círculo, no plano de coordenadas x y. A linha é uma linha vertical. O centro do círculo é (menos 3, 1) e tem um raio de 3 unidades. O ponto de interseção entre a linha e o círculo é (menos 6, 1).$
Figura 11.5.7

Exercício$\PageIndex{4}$

Resolva o sistema representando graficamente:$\left\{\begin{array}{l}{y=4} \\ {(x-2)^{2}+(y+3)^{2}=4}\end{array}\right.$

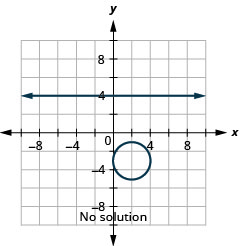
Responda: $Este gráfico mostra as equações de um sistema, y é igual a menos 4 e a quantidade x menos 2 ao quadrado mais a quantidade y mais 3 ao quadrado é igual a 4, que é um círculo, no plano de coordenadas x y. A linha é uma linha horizontal. O centro do círculo é (2, menos 3) e tem um raio de 2 unidades. Não há ponto de interseção entre a linha e o círculo, então o sistema não tem solução.$
Figura 11.5.8

Resolva um sistema de equações não lineares usando substituição

O método gráfico funciona bem quando os pontos de interseção são inteiros e são fáceis de ler no gráfico. Mas, mais frequentemente, é difícil ler as coordenadas dos pontos de interseção. O método de substituição é um método algébrico que funcionará bem em muitas situações. Funciona especialmente bem quando é fácil resolver uma das equações de uma das variáveis.

O método de substituição é muito semelhante ao método de substituição que usamos para sistemas de equações lineares. As etapas estão listadas abaixo para referência.

Resolva um sistema de equações não lineares por substituição

Identifique o gráfico de cada equação. Esboce as opções possíveis para a interseção.
Resolva uma das equações para qualquer variável.
Substitua a expressão da Etapa 2 pela outra equação.
Resolva a equação resultante.
Substitua cada solução na Etapa 4 em uma das equações originais para encontrar a outra variável.
Escreva cada solução como um par ordenado.
Verifique se cada par ordenado é uma solução para ambas as equações originais.

Exemplo$\PageIndex{3}$

Resolva o sistema usando a substituição:$\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x-3}\end{array}\right.$

Solução:

Tabela 11.5.3
Identifique cada gráfico.	$\left\{\begin{array}{ll}{9 x^{2}+y^{2}=9} & {\text { ellipse }} \\ {y=3 x-3} & {\text { line }}\end{array}\right.$
Esboce as opções possíveis para a interseção de uma elipse e uma linha.	$.$
A equação$y=3x-3$ foi resolvida para$y$.	$.$
	$.$
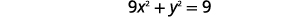$3x-3$Substitua por$y$ na primeira equação.	$.$
Resolva a equação para$x$.	$.$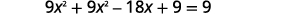
	$.$
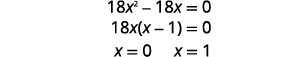Substitua$x=0$ e$x=1$ entre$y=3x-3$ para encontrar$y$ -.	$.$
	$.$
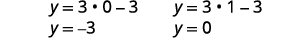	Os pares encomendados são$(0,-3), (1,0)$.
Verifique os dois pares ordenados em ambas as equações. $(0,-3)$ $\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot0^{2}+(-3)^{2}\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}3\cdot0-3} \\ {0+9\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}0-3} \\ {9=9}&\quad{-3=-3} \end{array}$ $(1,0)$ $\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot 1^{2}+(0)^{2}\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3\cdot 1-3} \\ {9+0\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3-3} \\ {9=9}&\quad{0=0} \end{array}$
	As soluções são$(0,-3), (1,0)$.

Exercício$\PageIndex{5}$

Resolva o sistema usando a substituição:$\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {y=\frac{1}{3} x-3}\end{array}\right.$

Responda: Sem solução

Exercício$\PageIndex{6}$

Resolva o sistema usando a substituição:$\left\{\begin{array}{l}{4 x^{2}+y^{2}=4} \\ {y=x+2}\end{array}\right.$

Responda: $\left(-\frac{4}{5}, \frac{6}{5}\right),(0,2)$

Até agora, cada sistema de equações não lineares teve pelo menos uma solução. O próximo exemplo mostrará outra opção.

Exemplo$\PageIndex{4}$

Resolva o sistema usando a substituição:$\left\{\begin{array}{l}{x^{2}-y=0} \\ {y=x-2}\end{array}\right.$

Solução:

Tabela 11.5.4
Identifique cada gráfico.	$\left\{\begin{array}{ll}{x^{2}-y=0} & {\text { parabola }} \\ {y=x-2} & {\text { line }}\end{array}\right.$
Esboce as opções possíveis para a interseção de uma parábola e uma linha.	$.$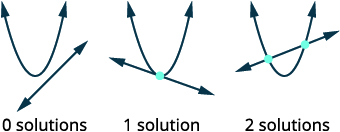
A equação$y=x-2$ foi resolvida para$y$.	$.$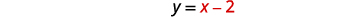
	$.$
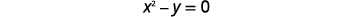$x-2$Substitua por$y$ na primeira equação.	$.$
Resolva a equação para$x$.	$.$
Isso não é um fator fácil, então podemos verificar o discriminante.
$\begin{array}{c}{b^{2}-4 a c} \\ {(-1)^{2}-4 \cdot 1 \cdot 2} \\ {-7}\end{array}$	O discriminante é negativo, então não há uma solução real. O sistema não tem solução.

Exercício$\PageIndex{7}$

Resolva o sistema usando a substituição:$\left\{\begin{array}{l}{x^{2}-y=0} \\ {y=2 x-3}\end{array}\right.$

Responda: Sem solução

Exercício$\PageIndex{8}$

Resolva o sistema usando a substituição:$\left\{\begin{array}{l}{y^{2}-x=0} \\ {y=3 x-2}\end{array}\right.$

Responda: $\left(\frac{4}{9},-\frac{2}{3}\right),(1,1)$

Resolva um sistema de equações não lineares usando eliminação

Quando estudamos sistemas de equações lineares, usamos o método de eliminação para resolver o sistema. Também podemos usar a eliminação para resolver sistemas de equações não lineares. Funciona bem quando as equações têm as duas variáveis ao quadrado. Ao usar a eliminação, tentamos fazer com que os coeficientes de uma variável sejam opostos, então, quando somamos as equações, essa variável é eliminada.

O método de eliminação é muito semelhante ao método de eliminação que usamos para sistemas de equações lineares. As etapas estão listadas para referência.

Resolva um sistema de equações por eliminação

Identifique o gráfico de cada equação. Esboce as opções possíveis para a interseção.
Escreva as duas equações na forma padrão.
Faça os coeficientes de uma variável oposta.
Decida qual variável você eliminará.
Multiplique uma ou ambas as equações para que os coeficientes dessa variável sejam opostos.
Adicione as equações resultantes da Etapa 3 para eliminar uma variável.
Resolva a variável restante.
Substitua cada solução da Etapa 5 em uma das equações originais. Em seguida, resolva a outra variável.
Escreva cada solução como um par ordenado.
Verifique se cada par ordenado é uma solução para ambas as equações originais.

Exemplo$\PageIndex{5}$

Resolva o sistema por eliminação:$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y=4}\end{array}\right.$

Solução:

Tabela 11.5.5
Identifique cada gráfico.	$.$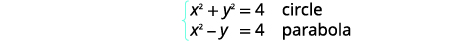
Esboce as opções possíveis para a interseção de um círculo e uma parábola.	$.$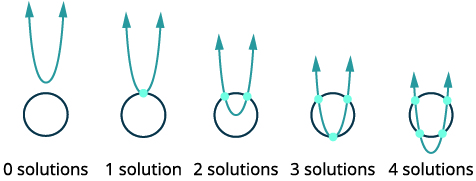
Ambas as equações estão na forma padrão.	$.$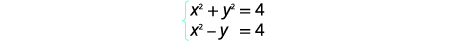
Para obter coeficientes opostos de$x^{2}$, multiplicaremos a segunda equação por$-1$.	$.$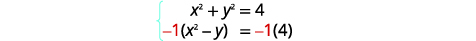
Simplifique.	$.$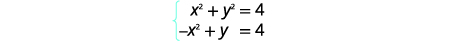
Adicione as duas equações para eliminar$x^{2}$/	$.$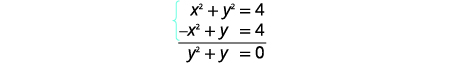
Resolver para$y$.	$.$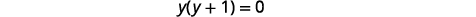
	$.$
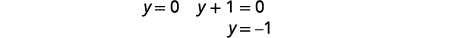Substitua$y=0$ e$y=-1$ em uma das equações originais. Em seguida, resolva por$x$.	$.$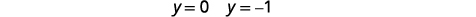
	$.$
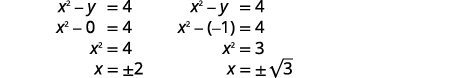Escreva cada solução como um par ordenado.	Os pares encomendados são$(-2,0)(2,0)$. $(\sqrt{3},-1)(-\sqrt{3},-1)$
Verifique se cada par ordenado é uma solução para ambas as equações originais.
Deixaremos as verificações de cada uma das quatro soluções para você.	As soluções são$(-2,0),(2,0),(\sqrt{3},-1)$,$(-\sqrt{3},-1)$ e.

Exercício$\PageIndex{9}$

Resolva o sistema por eliminação:$\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=9}\end{array}\right.$

Responda: $(-3,0),(3,0),(-2 \sqrt{2},-1),(2 \sqrt{2},-1)$

Exercício$\PageIndex{10}$

Resolva o sistema por eliminação:$\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {-x+y^{2}=1}\end{array}\right.$

Responda: $(-1,0),(0,1),(0,-1)$

Também há quatro opções quando consideramos um círculo e uma hipérbole.

Exemplo$\PageIndex{6}$

Resolva o sistema por eliminação:$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$

Solução:

Tabela 11.5.6
Identifique cada gráfico.	$\left\{\begin{array}{ll}{x^{2}+y^{2}=7} & {\text { circle }} \\ {x^{2}-y^{2}=1} & {\text { hyperbola }}\end{array}\right.$
Esboce as opções possíveis para a interseção de um círculo e uma hipérbole.	$.$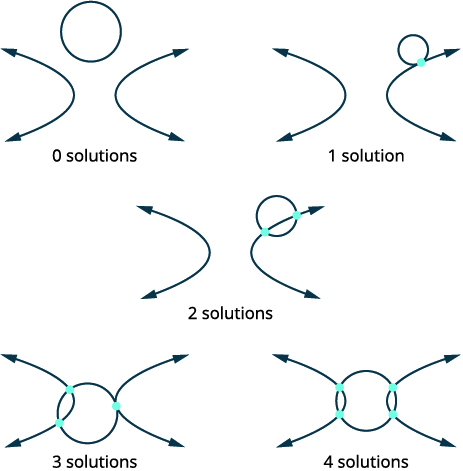
Ambas as equações estão na forma padrão.	$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$
Os coeficientes de$y^{2}$ são opostos, então adicionaremos as equações.	$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$ $2 x^{2}=8$
Simplifique.	$x^{2}=4$ $x=\pm 2$ $x=2 \quad x=-2$
Substitua$x=2$ e$x=-2$ em uma das equações originais. Em seguida, resolva por$y$.	$\begin{array}{rl}{x^{2}+y^{2} = 7} &\quad { x^{2}+y^{2}=7} \\ {2^{2}+y^{2}=7} & \quad{(-2)^{2}+y^{2}=7} \\ {4+y^{2}=7} &\quad {4+y^{2}=7} \\ {y^{2}=3} &\quad {y^{2}=3} \\ {y=\pm \sqrt{3}} &\quad {y=\pm \sqrt{3}}\end{array}$
Escreva cada solução como um par ordenado.	Os pares encomendados são$(-2, \sqrt{3}),(-2,-\sqrt{3})$,$(2, \sqrt{3}),$$(2,-\sqrt{3})$ e.
Verifique se o par ordenado é uma solução para ambas as equações originais.
Deixaremos as verificações de cada uma das quatro soluções para você.	As soluções são$(-2, \sqrt{3}),(-2,-\sqrt{3}),(2, \sqrt{3})$,$(2,-\sqrt{3})$ e.

Exercício$\PageIndex{11}$

Resolva o sistema por eliminação:$\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y^{2}-x^{2}=7}\end{array}\right.$

Responda: $(-3,-4),(-3,4),(3,-4),(3,4)$

Exercício$\PageIndex{12}$

Resolva o sistema por eliminação:$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y^{2}=4}\end{array}\right.$

Responda: $(-2,0),(2,0)$

Use um sistema de equações não lineares para resolver aplicações

Sistemas de equações não lineares podem ser usados para modelar e resolver muitas aplicações. Veremos uma situação geométrica cotidiana como nosso exemplo.

Exemplo$\PageIndex{7}$

A diferença dos quadrados de dois números é$15$. A soma dos números é$5$. Encontre os números.

Solução:

Tabela 11.5.7
Identifique o que estamos procurando.	Dois números diferentes.
Defina as variáveis.	$x$=primeiro número $y$=segundo número
Traduza as informações em um sistema de equações.
Primeira frase.	A diferença dos quadrados de dois números é$15$.
	$.$
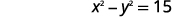Segunda frase.	A soma dos números é$5$.
	$.$
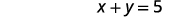Resolva o sistema por substituição.	$.$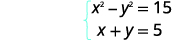
Resolva a segunda equação para$x$.	$.$
Substitua$x$ na primeira equação.	$.$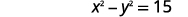
	$.$
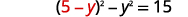Expanda e simplifique.	$.$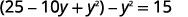
	$.$
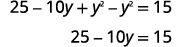Resolver para$y$.	$.$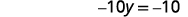
	$.$
Substitua novamente na segunda equação.	$.$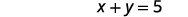
	$.$
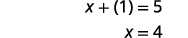	Os números são$1$$4$ e.

Exercício$\PageIndex{13}$

A diferença dos quadrados de dois números é$−20$. A soma dos números é$10$. Encontre os números.

Responda: $4$e$6$

Exercício$\PageIndex{14}$

A diferença dos quadrados de dois números é$35$. A soma dos números é$−1$. Encontre os números.

Responda: $-18$e$17$

Exemplo$\PageIndex{8}$

Myra comprou uma$25$ “pequena” TV para sua cozinha. O tamanho de uma TV é medido na diagonal da tela. A tela também tem uma área de polegadas$300$ quadradas. Quais são o comprimento e a largura da tela da TV?

Solução:

Tabela 11.5.8
Identifique o que estamos procurando.	O comprimento e a largura do retângulo.
Defina as variáveis.	Seja$x$ = largura do retângulo $y$=comprimento do retângulo
Desenhe um diagrama para ajudar a visualizar a situação.	$.$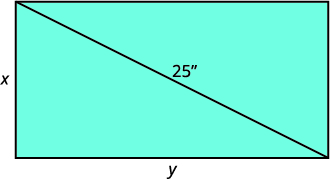
	A área é em polegadas$300$ quadradas.
Traduza as informações em um sistema de equações.	A diagonal do triângulo direito é em$25$ polegadas.
	$.$
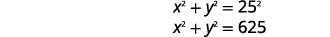	A área do retângulo é de polegadas$300$ quadradas.
	$.$
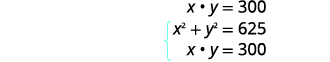Resolva o sistema usando a substituição.	$.$
Resolva a segunda equação para$x$.	$.$
Substitua$x$ na primeira equação.	$.$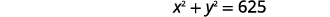
	$.$
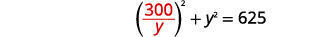Simplifique.	$.$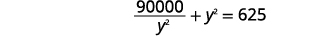
Multiplique por$y^{2}$ para limpar as frações.	$.$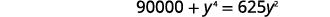
Coloque na forma padrão.	$.$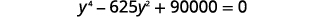
Resolva por fatoração.	$.$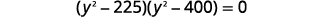
	$.$
	$.$
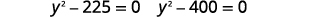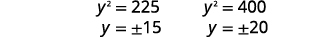Como$y$ é um lado do retângulo, descartamos os valores negativos.	$.$
Substitua novamente na segunda equação.	$.$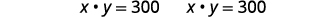
	$.$
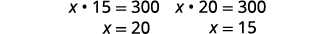	Se o comprimento for$15$ polegadas, a largura será$20$ polegadas.
	Se o comprimento for$20$ polegadas, a largura será$15$ polegadas.

Exercício$\PageIndex{15}$

Edgar comprou uma$20$ “pequena” TV para sua garagem. O tamanho de uma TV é medido na diagonal da tela. A tela também tem uma área de polegadas$192$ quadradas. Quais são o comprimento e a largura da tela da TV?

Responda: Se o comprimento for$12$ polegadas, a largura será$16$ polegadas. Se o comprimento for$16$ polegadas, a largura será$12$ polegadas.

Exercício$\PageIndex{16}$

A família Harper comprou um pequeno micro-ondas para o quarto da família. A diagonal da porta mede$15$ polegadas. A porta também tem uma área de polegadas$108$ quadradas. Quais são o comprimento e a largura da porta do micro-ondas?

Responda: Se o comprimento for$12$ polegadas, a largura será$9$ polegadas. Se o comprimento for$9$ polegadas, a largura será$12$ polegadas.

Acesse esses recursos on-line para obter instruções adicionais e praticar a resolução de equações não lineares.

Sistemas de equações não lineares
Resolva um sistema de equações não lineares
Resolva um sistema de equações não lineares por eliminação
Sistema de equações não lineares — Aplicação de área e perímetro

Conceitos chave

Como resolver um sistema de equações não lineares por meio de gráficos.
1. Identifique o gráfico de cada equação. Esboce as opções possíveis para a interseção.
2. Faça um gráfico da primeira equação.
3. Faça um gráfico da segunda equação no mesmo sistema de coordenadas retangulares.
4. Determine se os gráficos se cruzam.
5. Identifique os pontos de interseção.
6. Verifique se cada par ordenado é uma solução para ambas as equações originais.
Como resolver um sistema de equações não lineares por substituição.
1. Identifique o gráfico de cada equação. Esboce as opções possíveis para a interseção.
2. Resolva uma das equações para qualquer variável.
3. Substitua a expressão da Etapa 2 pela outra equação.
4. Resolva a equação resultante.
5. Substitua cada solução na Etapa 4 em uma das equações originais para encontrar a outra variável.
6. Escreva cada solução como um par ordenado.
7. Verifique se cada par ordenado é uma solução para ambas as equações originais.
Como resolver um sistema de equações por eliminação.
1. Identifique o gráfico de cada equação. Esboce as opções possíveis para a interseção.
2. Escreva as duas equações na forma padrão.
3. Faça os coeficientes de uma variável oposta.
  Decida qual variável você eliminará.
  Multiplique uma ou ambas as equações para que os coeficientes dessa variável sejam opostos.
4. Adicione as equações resultantes da Etapa 3 para eliminar uma variável.
5. Resolva a variável restante.
6. Substitua cada solução da Etapa 5 em uma das equações originais. Em seguida, resolva a outra variável.
7. Escreva cada solução como um par ordenado.
8. Verifique se cada par ordenado é uma solução para ambas as equações originais.

Identifique cada gráfico.	\(\left\{\begin{array}{ll}{x^{2}+y^{2}=7} & {\text { circle }} \\ {x^{2}-y^{2}=1} & {\text { hyperbola }}\end{array}\right.\)
Esboce as opções possíveis para a interseção de um círculo e uma hipérbole.	$.$
Ambas as equações estão na forma padrão.	\(\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.\)
Os coeficientes de\(y^{2}\) são opostos, então adicionaremos as equações.	\(\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.\) \(2 x^{2}=8\)
Simplifique.	\(x^{2}=4\) \(x=\pm 2\) \(x=2 \quad x=-2\)
Substitua\(x=2\) e\(x=-2\) em uma das equações originais. Em seguida, resolva por\(y\).	\(\begin{array}{rl}{x^{2}+y^{2} = 7} &\quad { x^{2}+y^{2}=7} \\ {2^{2}+y^{2}=7} & \quad{(-2)^{2}+y^{2}=7} \\ {4+y^{2}=7} &\quad {4+y^{2}=7} \\ {y^{2}=3} &\quad {y^{2}=3} \\ {y=\pm \sqrt{3}} &\quad {y=\pm \sqrt{3}}\end{array}\)
Escreva cada solução como um par ordenado.	Os pares encomendados são\((-2, \sqrt{3}),(-2,-\sqrt{3})\),\((2, \sqrt{3}),\)\((2,-\sqrt{3})\) e.
Verifique se o par ordenado é uma solução para ambas as equações originais.
Deixaremos as verificações de cada uma das quatro soluções para você.	As soluções são\((-2, \sqrt{3}),(-2,-\sqrt{3}),(2, \sqrt{3})\),\((2,-\sqrt{3})\) e.

Definição\(\PageIndex{1}\)

Exemplo\(\PageIndex{1}\)

Exercício\(\PageIndex{1}\)

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{2}\)

Exercício\(\PageIndex{3}\)

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{3}\)

Exercício\(\PageIndex{5}\)

Exercício\(\PageIndex{6}\)

Exemplo\(\PageIndex{4}\)

Exercício\(\PageIndex{7}\)

Exercício\(\PageIndex{8}\)

Exemplo\(\PageIndex{5}\)

Exercício\(\PageIndex{9}\)

Exercício\(\PageIndex{10}\)

Exemplo\(\PageIndex{6}\)

Exercício\(\PageIndex{11}\)

Exercício\(\PageIndex{12}\)

Exemplo\(\PageIndex{7}\)

Exercício\(\PageIndex{13}\)

Exercício\(\PageIndex{14}\)

Exemplo\(\PageIndex{8}\)

Exercício\(\PageIndex{15}\)

Exercício\(\PageIndex{16}\)

Identifique cada gráfico.	\(\left\{\begin{array}{ll}{x-y=-2} & {\text { line }} \\ {y=x^{2}} & {\text { parabola }}\end{array}\right.\)
Esboce as opções possíveis para a interseção de uma parábola e uma linha.	$.$
Faça um gráfico da linha,\(x-y=-2\). Forma de interceptação de inclinação\(y=x+2\). Faça um gráfico da parábola,\(y=x^{2}\).	$.$
Identifique os pontos de interseção.	Os pontos de interseção parecem ser\((2,3)\)\((-1,1)\) e.
Verifique se cada solução torna as duas equações verdadeiras. \((2,4)\) \(\begin{array} {r l } {x-y=-2}\quad\quad {y=x^{2}} \\ {2-4\stackrel{?}{=}-2}\quad\quad {4\stackrel{?}{=}2^{2}} \\ {-2 = -2}\quad\quad\:{4 = 4} \end{array}\) \((-1,1)\) \(\begin{array} {l l } {x-y=-2}\quad\quad {y=x^{2}} \\ {-1-1\stackrel{?}{=}-2}\:\quad {1\stackrel{?}{=}(-1)^{2}} \\ {-2 = -2}\quad\quad\quad{1 = 1} \end{array}\)
	As soluções são\((2,4)\)\((-1,1)\) e.

Identifique cada gráfico.	\(\left\{\begin{array}{ll}{y=-1} & {\text { line }} \\ {(x-2)^{2}+(y+3)^{2}=4} & {\text { circle }}\end{array}\right.\)
Esboce as opções possíveis para a interseção de um círculo e uma linha.	$.$
Faça um gráfico do círculo,\((x-2)^{2}+(y+3)^{2}=4\) Centro:\((2,-3)\) raio:\(2\) Faça um gráfico da linha,\(y=-1\). É uma linha horizontal.	$.$
Identifique os pontos de interseção.	O ponto de interseção parece ser\((2,-1)\).
Verifique se a solução torna as duas equações verdadeiras. \((2,-1)\) \(\begin{array} {r r} {(x-2)^{2}+(y+3)^{2}=4} \quad\quad {y=-1} \\ {(2-2)^{2}+(-1+3)^{2}\stackrel{?}{=}4}\quad{-1=-1} \\ {(0)^{2}+(2)^{2}\stackrel{?}{=}4}\quad\quad\quad\quad\quad \\ {4=4}\quad\quad\quad\quad\quad \end{array}\)
	A solução é\((2,-1)\)

Identifique cada gráfico.	\(\left\{\begin{array}{ll}{9 x^{2}+y^{2}=9} & {\text { ellipse }} \\ {y=3 x-3} & {\text { line }}\end{array}\right.\)
Esboce as opções possíveis para a interseção de uma elipse e uma linha.	$.$
A equação\(y=3x-3\) foi resolvida para\(y\).	$.$
	$.$
\(3x-3\)Substitua por\(y\) na primeira equação.	$.$
Resolva a equação para\(x\).	$.$
	$.$
Substitua\(x=0\) e\(x=1\) entre\(y=3x-3\) para encontrar\(y\) -.	$.$
	$.$
	Os pares encomendados são\((0,-3), (1,0)\).
Verifique os dois pares ordenados em ambas as equações. \((0,-3)\) \(\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot0^{2}+(-3)^{2}\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}3\cdot0-3} \\ {0+9\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}0-3} \\ {9=9}&\quad{-3=-3} \end{array}\) \((1,0)\) \(\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot 1^{2}+(0)^{2}\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3\cdot 1-3} \\ {9+0\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3-3} \\ {9=9}&\quad{0=0} \end{array}\)
	As soluções são\((0,-3), (1,0)\).

Identifique cada gráfico.	\(\left\{\begin{array}{ll}{x^{2}-y=0} & {\text { parabola }} \\ {y=x-2} & {\text { line }}\end{array}\right.\)
Esboce as opções possíveis para a interseção de uma parábola e uma linha.	$.$
A equação\(y=x-2\) foi resolvida para\(y\).	$.$
	$.$
\(x-2\)Substitua por\(y\) na primeira equação.	$.$
Resolva a equação para\(x\).	$.$
Isso não é um fator fácil, então podemos verificar o discriminante.
\(\begin{array}{c}{b^{2}-4 a c} \\ {(-1)^{2}-4 \cdot 1 \cdot 2} \\ {-7}\end{array}\)	O discriminante é negativo, então não há uma solução real. O sistema não tem solução.