Skip to main content
Global

Capítulo 11 Exercícios de revisão

  1. Last updated
  2. Save as PDF
  • Page ID
    183711

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Exercícios de revisão de

    Fórmulas de distância e ponto médio; círculos

    Exercício\(\PageIndex{1}\) Use the Distance Formula

    Nos exercícios a seguir, encontre a distância entre os pontos. Arredonde para o décimo mais próximo, se necessário.

    1. \((-5,1)\)e\((-1,4)\)
    2. \((-2,5)\)e\((1,5)\)
    3. \((8,2)\)e\((-7,-3)\)
    4. \((1,-4)\)e\((5,-5)\)
    Resposta

    2. \(d=3\)

    4. \(d=\sqrt{17}, d \approx 4.1\)

    Exercício\(\PageIndex{2}\) Use the Midpoint Formula

    Nos exercícios a seguir, encontre o ponto médio dos segmentos de linha cujos pontos finais são fornecidos.

    1. \((-2,-6)\)e\((-4,-2)\)
    2. \((3,7)\)e\((5,1)\)
    3. \((-8,-10)\)e\((9,5)\)
    4. \((-3,2)\)e\((6,-9)\)
    Resposta

    2. \((4,4)\)

    4. \(\left(\frac{3}{2},-\frac{7}{2}\right)\)

    Exercício\(\PageIndex{3}\) Write the Equation of a Circle in Standard Form

    Nos exercícios a seguir, escreva a forma padrão da equação do círculo com as informações fornecidas.

    1. o raio é\(15\) e o centro é\((0,0)\)
    2. o raio é\(\sqrt{7}\) e o centro é\((0,0)\)
    3. o raio é\(9\) e o centro é\((-3,5)\)
    4. o raio é\(7\) e o centro é\((-2,-5)\)
    5. centro é\((3,6)\) e um ponto no círculo é\((3,-2)\)
    6. centro é\((2,2)\) e um ponto no círculo é\((4,4)\)
    Resposta

    2. \(x^{2}+y^{2}=7\)

    4. \((x+2)^{2}+(y+5)^{2}=49\)

    6. \((x-2)^{2}+(y-2)^{2}=8\)

    Exercício\(\PageIndex{4}\) Graph a Circle

    Nos exercícios a seguir,

    1. Encontre o centro e o raio e, em seguida,
    2. Faça um gráfico de cada círculo.
    1. \(2 x^{2}+2 y^{2}=450\)
    2. \(3 x^{2}+3 y^{2}=432\)
    3. \((x+3)^{2}+(y-5)^{2}=81\)
    4. \((x+2)^{2}+(y+5)^{2}=49\)
    5. \(x^{2}+y^{2}-6 x-12 y-19=0\)
    6. \(x^{2}+y^{2}-4 y-60=0\)
    Resposta

    2.

    1. raio:\(12,\) centro:\((0,0)\)
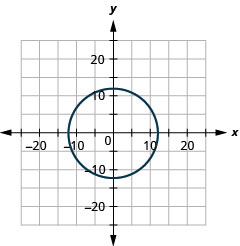
    A figura mostra um círculo representado graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 20 a 20. O eixo y do plano vai de menos 15 a 15. O centro do círculo é (0, 0) e o raio do círculo é 12.
    Figura 11.E.1

    4.

    1. raio:\(7,\) centro:\((-2,-5)\)
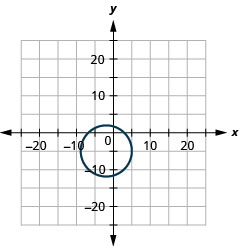
    A figura mostra um círculo representado graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 20 a 20. O eixo y do plano vai de menos 15 a 15. O centro do círculo é (menos 2, menos 5) e o raio do círculo é 7.
    Figura 11.E.2

    6.

    1. raio:\(8,\) centro:\((0,2)\)
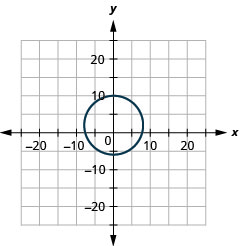
    A figura mostra um círculo representado graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 20 a 20. O eixo y do plano vai de menos 15 a 15. O centro do círculo é (0, 2) e o raio do círculo é 8.
    Figura 11.E.3

    Parábolas

    Exercício\(\PageIndex{5}\) Graph Vertical Parabolas

    Nos exercícios a seguir, represente graficamente cada equação usando suas propriedades.

    1. \(y=x^{2}+4 x-3\)
    2. \(y=2 x^{2}+10 x+7\)
    3. \(y=-6 x^{2}+12 x-1\)
    4. \(y=-x^{2}+10 x\)
    Resposta

    2.

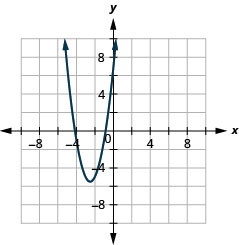
    A figura mostra uma parábola de abertura ascendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 7 a 7. O vértice é (menos cinco metades, menos onze metades) e a parábola passa pelos pontos (menos 4, menos 1) e (menos 1, menos 1).
    Figura 11.E.4

    4.

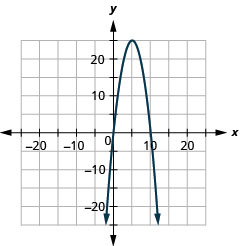
    A figura mostra uma parábola de abertura descendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 36 a 36. O eixo y do plano vai de menos 26 a 26. O vértice é (5, 25) e a parábola passa pelos pontos (2, 16) e (8, 16).
    Figura 11.E.5
    Exercício\(\PageIndex{6}\) Graph Vertical Parabolas

    Nos exercícios a seguir,

    1. Escreva a equação na forma padrão e, em seguida,
    2. Use as propriedades da forma padrão para representar graficamente a equação.
    1. \(y=x^{2}+4 x+7\)
    2. \(y=2 x^{2}-4 x-2\)
    3. \(y=-3 x^{2}-18 x-29\)
    4. \(y=-x^{2}+12 x-35\)
    Resposta

    2.

    1. \(y=2(x-1)^{2}-4\)
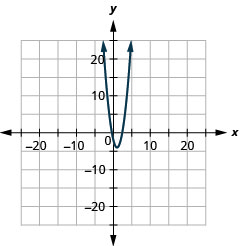
    A figura mostra uma parábola de abertura ascendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 22 a 22. O eixo y do plano vai de menos 16 a 16. O vértice é (1, menos 4) e a parábola passa pelos pontos (0, menos 2) e (2, menos 2).
    Figura 11.E.6

    4.

    1. \(y=-(x-6)^{2}+1\)
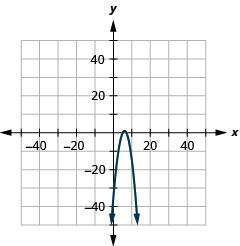
    A figura mostra uma parábola de abertura descendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 60 a 60. O eixo y do plano vai de menos 46 a 46. O vértice é (6, 1) e a parábola passa pelos pontos (5, 0) e (7, 0).
    Figura 11.E.7
    Exercício\(\PageIndex{7}\) Graph Horizontal Parabolas

    Nos exercícios a seguir, represente graficamente cada equação usando suas propriedades.

    1. \(x=2 y^{2}\)
    2. \(x=2 y^{2}+4 y+6\)
    3. \(x=-y^{2}+2 y-4\)
    4. \(x=-3 y^{2}\)
    Resposta

    2.

    A figura mostra uma parábola de abertura à direita representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 8 a 8. O vértice é (4, menos 1) e a parábola passa pelos pontos (6, 0) e (6, menos 2).
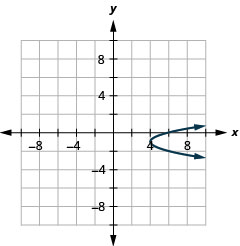
    Figura 11.E.8

    4.

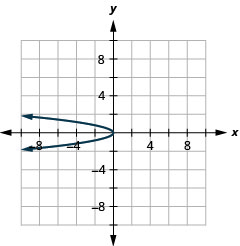
    A figura mostra uma parábola de abertura à esquerda representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 8 a 8. O vértice é (0, 0) e a parábola passa pelos pontos (menos 3, 1) e (menos 3, menos 1).
    Figura 11.E.9
    Exercício\(\PageIndex{8}\) Graph Horizontal Parabolas

    Nos exercícios a seguir,

    1. Escreva a equação na forma padrão e, em seguida,
    2. Use as propriedades da forma padrão para representar graficamente a equação.
    1. \(x=4 y^{2}+8 y\)
    2. \(x=y^{2}+4 y+5\)
    3. \(x=-y^{2}-6 y-7\)
    4. \(x=-2 y^{2}+4 y\)
    Resposta

    2.

    1. \(x=(y+2)^{2}+1\)
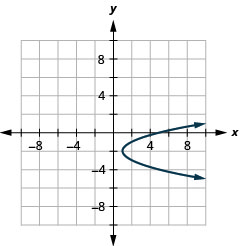
    A figura mostra uma parábola de abertura à direita representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 8 a 8. O vértice é (1, menos 2) e a parábola passa pelos pontos (5, 0) e (5, menos 4).
    Figura 11.E.10

    4.

    1. \(x=-2(y-1)^{2}+2\)
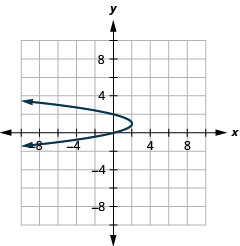
    A figura mostra uma parábola de abertura à esquerda representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 8 a 8. O vértice é (2, menos 3) e a parábola passa pelos pontos (0, 2) e (0, 0).
    Figura 11.E.11
    Exercício\(\PageIndex{9}\) Solve Applications with Parabolas

    Nos exercícios a seguir, crie a equação do arco parabólico formado na base da ponte mostrada. Dê a resposta na forma padrão.

    1.

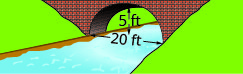
    A figura mostra um arco parabólico formado na base da ponte. O arco tem 5 pés de altura e 20 pés de largura.
    Figura 11.E.12

    2.

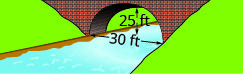
    A figura mostra um arco parabólico formado na base da ponte. O arco tem 25 pés de altura e 30 pés de largura.
    Figura 11.E.13
    Resposta

    2. \(y=-\frac{1}{9} x^{2}+\frac{10}{3} x\)

    Elipses

    Exercício\(\PageIndex{10}\) Graph an Ellipse with Center at the Origin

    Nos exercícios a seguir, represente graficamente cada elipse.

    1. \(\frac{x^{2}}{36}+\frac{y^{2}}{25}=1\)
    2. \(\frac{x^{2}}{4}+\frac{y^{2}}{81}=1\)
    3. \(49 x^{2}+64 y^{2}=3136\)
    4. \(9 x^{2}+y^{2}=9\)
    Resposta

    2.

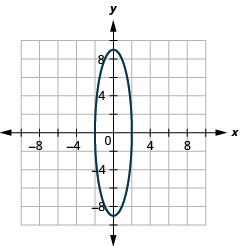
    A figura mostra uma elipse representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 14 a 14. O eixo y do plano vai de menos 10 a 10. A elipse tem um centro em (0, 0), um eixo maior vertical, vértices em (0, mais ou menos 9) e co-vértices em (mais ou menos 2, 0).
    Figura 11.E.14

    4.

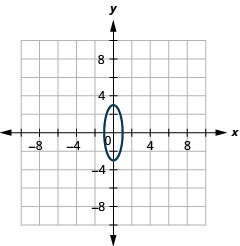
    A figura mostra uma elipse representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 9 a 9. O eixo y do plano vai de menos 7 a 7. A elipse tem um centro em (0, 0), um eixo maior vertical, vértices em (0, mais ou menos 3) e co-vértices em (mais ou menos 1, 0).
    Figura 11.E.15
    Exercício\(\PageIndex{11}\) Find the Equation of an Ellipse with Center at the Origin

    Nos exercícios a seguir, encontre a equação da elipse mostrada no gráfico.

    1.

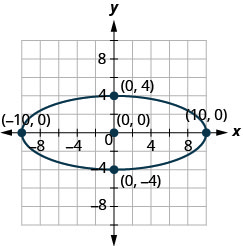
    A figura mostra uma elipse representada graficamente no plano de coordenadas x y. A elipse tem um centro em (0, 0), um eixo maior horizontal, vértices em (mais ou menos 10, 0) e co-vértices em (0, mais ou menos 4).
    Figura 11.E.16

    2.

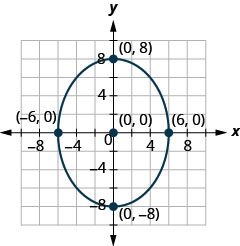
    A figura mostra uma elipse representada graficamente no plano de coordenadas x y. A elipse tem um centro em (0, 0), um eixo maior vertical, vértices em (0, mais ou menos 8) e co-vértices em (mais ou menos 6, 0).
    Figura 11.E.17
    Resposta

    2. \(\frac{x^{2}}{36}+\frac{y^{2}}{64}=1\)

    Exercício\(\PageIndex{12}\) Graph an Ellipse with Center Not at the Origin

    Nos exercícios a seguir, represente graficamente cada elipse.

    1. \(\frac{(x-1)^{2}}{25}+\frac{(y-6)^{2}}{4}=1\)
    2. \(\frac{(x+4)^{2}}{16}+\frac{(y+1)^{2}}{9}=1\)
    3. \(\frac{(x-5)^{2}}{16}+\frac{(y+3)^{2}}{36}=1\)
    4. \(\frac{(x+3)^{2}}{9}+\frac{(y-2)^{2}}{25}=1\)
    Resposta

    2.

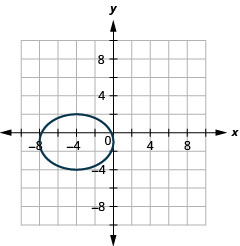
    A figura mostra uma elipse representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 14 a 14. O eixo y do plano vai de menos 10 a 10. A elipse tem um centro em (menos 4, menos 1), um eixo maior horizontal, vértices em (menos 8, menos 1) e (0, menos 1) e co-vértices em (menos 4, 2) e (menos 4, menos 4).
    Figura 11.E.18

    4.

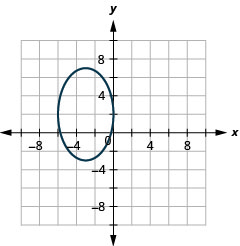
    A figura mostra uma elipse representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 14 a 14. O eixo y do plano vai de menos 10 a 10. A elipse tem um centro em (menos 3, 2), um eixo maior vertical, vértices em (menos 3, 7) e (menos 3, menos 3) e co-vértices em (menos 6, 2) e (0, 2).
    Figura 11.E.19
    Exercício\(\PageIndex{13}\) Graph an Ellipse with Center Not at the Origin

    Nos exercícios a seguir,

    1. Escreva a equação na forma padrão e
    2. Gráfico.
    1. \(x^{2}+y^{2}+12 x+40 y+120=0\)
    2. \(25 x^{2}+4 y^{2}-150 x-56 y+321=0\)
    3. \(25 x^{2}+4 y^{2}+150 x+125=0\)
    4. \(4 x^{2}+9 y^{2}-126 x+405=0\)
    Resposta

    2.

    1. \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
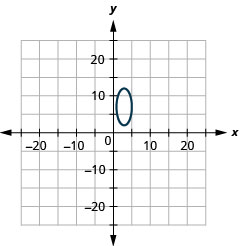
    A figura mostra uma elipse representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 18 a 18. O eixo y do plano vai de menos 14 a 14. A elipse tem um centro em (3, 7), um eixo maior vertical, vértices em (3, 2) e (3, 12) e co-vértices em (menos 1, 7) e (5, 7).
    Figura 11.E.20

    4.

    1. \(\frac{x^{2}}{9}+\frac{(y-7)^{2}}{4}=1\)
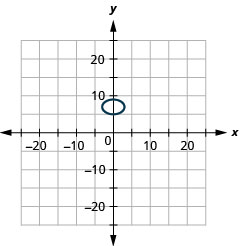
    A figura mostra uma elipse representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 15 a 15. O eixo y do plano vai de menos 11 a 11. A elipse tem um centro em (0, 7), um eixo maior horizontal, vértices em (3, 7) e (menos 3, 7) e co-vértices em (0, 5) e (0, 9).
    Figura 11.E.21
    Exercício\(\PageIndex{14}\) Solve Applications with Ellipses

    Nos exercícios a seguir, escreva a equação da elipse descrita.

    1. Um cometa se move em uma órbita elíptica ao redor do sol. O mais próximo que o cometa chega do sol é aproximadamente\(10\) AU e o mais distante é aproximadamente\(90\) AU. O sol é um dos focos da órbita elíptica. Deixando a elipse centrar na origem e rotulando os eixos em AU, a órbita ficará parecida com a figura abaixo. Use o gráfico para escrever uma equação para a órbita elíptica do cometa.
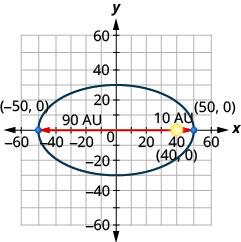
    A figura mostra um modelo de uma órbita elíptica ao redor do sol no plano de coordenadas x y. A elipse tem um centro em (0, 0), um eixo principal horizontal, vértices marcados em (mais ou menos 50, 0), o sol marcado como um foco e rotulado (50, 0), a distância mais próxima que o cometa está do sol marcada como 10 A U e a mais distante um cometa está do sol marcado como 90 A U.
    Figura 11.E.22
    Resposta

    1. Resolver

    Hipérbolas

    Exercício\(\PageIndex{15}\) Graph a Hyperbola with Center at \((0,0)\)

    Nos exercícios a seguir, faça um gráfico.

    1. \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\)
    2. \(\frac{y^{2}}{49}-\frac{x^{2}}{16}=1\)
    3. \(9 y^{2}-16 x^{2}=144\)
    4. \(16 x^{2}-4 y^{2}=64\)
    Resposta

    1.

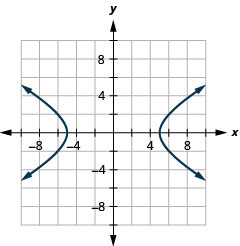
    A figura mostra uma hipérbole representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 12 a 12. O eixo y do plano vai de menos 9 a 9. A hipérbole tem um centro em (0, 0) e ramificações que passam pelos vértices (mais ou menos 5, 0) e que se abrem para a esquerda e para a direita.
    Figura 11.E.23

    3.

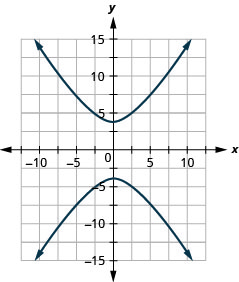
    A figura mostra uma hipérbole representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 19 a 19. O eixo y do plano vai de menos 15 a 15. A hipérbole tem um centro em (0, 0) e ramificações que passam pelos vértices (0, mais ou menos 4) e que se abrem para cima e para baixo.
    Figura 11.E.24
    Exercício\(\PageIndex{16}\) Graph a Hyperbola with Center at \((h,k)\)

    Nos exercícios a seguir, faça um gráfico.

    1. \(\frac{(x+1)^{2}}{4}-\frac{(y+1)^{2}}{9}=1\)
    2. \(\frac{(x-2)^{2}}{4}-\frac{(y-3)^{2}}{16}=1\)
    3. \(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{9}=1\)
    4. \(\frac{(y-1)^{2}}{25}-\frac{(x-2)^{2}}{9}=1\)
    Resposta

    1.

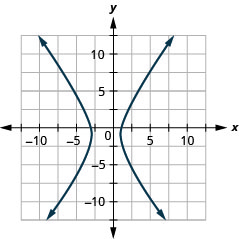
    A figura mostra uma hipérbole representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 14 a 14. O eixo y do plano vai de menos 10 a 10. A hipérbole tem um centro em (menos 1, menos 1) e ramificações que passam pelos vértices (menos 3, menos 1) e (1, menos 1), e que se abrem para a esquerda e para a direita.
    Figura 11.E.25

    3.

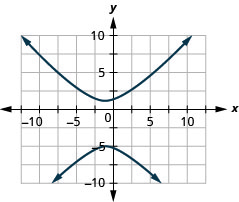
    A figura mostra uma hipérbole representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 14 a 14. O eixo y do plano vai de menos 10 a 10. A hipérbole tem um centro em (menos 1, menos 2) e ramificações que passam pelos vértices (menos 1, 1) e (menos 1, menos 5) e que se abrem para cima e para baixo.
    Figura 11.E.26
    Exercício\(\PageIndex{17}\) Graph a Hyperbola with Center at \((h,k)\)

    Nos exercícios a seguir,

    1. Escreva a equação na forma padrão e
    2. Gráfico.
    1. \(4 x^{2}-16 y^{2}+8 x+96 y-204=0\)
    2. \(16 x^{2}-4 y^{2}-64 x-24 y-36=0\)
    3. \(4 y^{2}-16 x^{2}+32 x-8 y-76=0\)
    4. \(36 y^{2}-16 x^{2}-96 x+216 y-396=0\)
    Resposta

    1.

    1. \(\frac{(x+1)^{2}}{16}-\frac{(y-3)^{2}}{4}=1\)
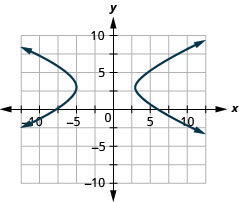
    A figura mostra uma hipérbole representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 14 a 14. O eixo y do plano vai de menos 10 a 10. A hipérbole tem um centro em (menos 1, 3) e ramificações que passam pelos vértices (menos 5, 3) e (3, 3), e que se abrem para a esquerda e para a direita.
    Figura 11.E.27

    3.

    1. \(\frac{(y-1)^{2}}{16}-\frac{(x-1)^{2}}{4}=1\)
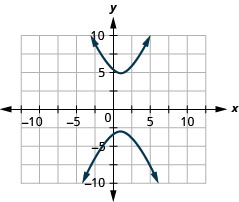
    A figura mostra uma hipérbole representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 14 a 14. O eixo y do plano vai de menos 10 a 10. A hipérbole tem um centro em (1, 1) e ramificações que passam pelos vértices (1, menos 3) e (1, 5) e que se abrem para cima e para baixo.
    Figura 11.E.28
    Exercício\(\PageIndex{18}\) Identify the Graph of Each Equation as a Circle, Parabola, Ellipse, or Hyperbola

    Nos exercícios a seguir, identifique o tipo de gráfico.

      1. \(16 y^{2}-9 x^{2}-36 x-96 y-36=0\)
      2. \(x^{2}+y^{2}-4 x+10 y-7=0\)
      3. \(y=x^{2}-2 x+3\)
      4. \(25 x^{2}+9 y^{2}=225\)
      1. \(x^{2}+y^{2}+4 x-10 y+25=0\)
      2. \(y^{2}-x^{2}-4 y+2 x-6=0\)
      3. \(x=-y^{2}-2 y+3\)
      4. \(16 x^{2}+9 y^{2}=144\)
    Resposta

    1.

    1. Hyperbole
    2. Círculo
    3. Parábola
    4. Elipse

    Resolva sistemas de equações não lineares

    Exercício\(\PageIndex{19}\) Solve a System of Nonlinear Equations Using Graphing

    Nos exercícios a seguir, resolva o sistema de equações usando gráficos.

    1. \(\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y=-5}\end{array}\right.\)
    Resposta

    1.

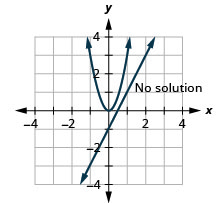
    A figura mostra uma parábola e uma linha representadas graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 5 a 5. O eixo y do plano vai de menos 4 a 4. A parábola tem um vértice em (0, 0) e se abre para cima. A linha tem uma inclinação de 2 com um intercepto y em menos 1. A parábola e a linha não se cruzam, então o sistema não tem solução.
    Figura 11.E.29

    3.

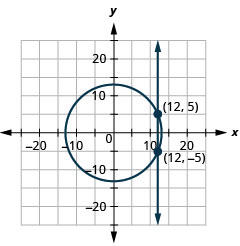
    A figura mostra um círculo e uma linha representados graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 20 a 20. O eixo y do plano vai de menos 15 a 15. O círculo tem um centro em (0, 0) e um raio de 13. A linha é vertical. O círculo e a linha se cruzam nos pontos (12, 5) e (12, menos 5), que são rotulados. A solução do sistema é (12, 5) e (12, menos 5)
    Figura 11.E.30
    Exercício\(\PageIndex{20}\) Solve a System of Nonlinear Equations Using Substitution

    Nos exercícios a seguir, resolva o sistema de equações usando a substituição.

    1. \(\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=-2 x+2}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x-y=4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {y-x=5}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {2 x-y=1}\end{array}\right.\)
    Resposta

    1. \((-1,4)\)

    3. Sem solução

    Exercício\(\PageIndex{21}\) Solve a System of Nonlinear Equations Using Elimination

    Nos exercícios a seguir, resolva o sistema de equações usando a eliminação.

    1. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y-1=0}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}-y^{2}=5} \\ {-2 x^{2}-3 y^{2}=-30}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {3 y^{2}-4 x=12}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=14} \\ {x^{2}-y^{2}=16}\end{array}\right.\)
    Resposta

    1. \((-\sqrt{7}, 3),(\sqrt{7}, 3)\)

    3. \((-3,0),(0,-2),(0,2)\)

    Exercício\(\PageIndex{22}\) Use a System of Nonlinear Equations to Solve Applications

    Nos exercícios a seguir, resolva o problema usando um sistema de equações.

    1. A soma dos quadrados de dois números é\(25\). A diferença dos números é\(1\). Encontre os números.
    2. A diferença dos quadrados de dois números é\(45\). A diferença entre o quadrado do primeiro número e o dobro do quadrado do segundo número é\(9\). Encontre os números.
    3. O perímetro de um retângulo é de\(58\) metros e sua área é de metros\(210\) quadrados. Encontre o comprimento e a largura do retângulo.
    4. Colton comprou um micro-ondas maior para sua cozinha. A diagonal da frente do micro-ondas mede\(34\) polegadas. A frente também tem uma área de polegadas\(480\) quadradas. Quais são o comprimento e a largura do micro-ondas?
    Resposta

    1. \(-3\)e\(-4\) ou\(4\) e\(3\)

    3. Se o comprimento for\(14\) polegadas, a largura será\(15\) polegadas. Se o comprimento for\(15\) polegadas, a largura será\(14\) polegadas.

    Teste prático

    Exercício\(\PageIndex{23}\)

    Nos exercícios a seguir, encontre a distância entre os pontos e o ponto médio do segmento de linha com os pontos finais fornecidos. Arredonde para o décimo mais próximo, conforme necessário.

    1. \((-4,-3)\)e\((-10,-11)\)
    2. \((6,8)\)e\((-5,-3)\)
    Resposta

    1. distância:\(10,\) ponto médio:\((-7,-7)\)

    Exercício\(\PageIndex{24}\)

    Nos exercícios a seguir, escreva a forma padrão da equação do círculo com as informações fornecidas.

    1. o raio é\(11\) e o centro é\((0,0)\)
    2. o raio é\(12\) e o centro é\((10,-2)\)
    3. centro é\((-2,3)\) e um ponto no círculo é\((2,-3)\)
    4. Encontre a equação da elipse mostrada no gráfico.
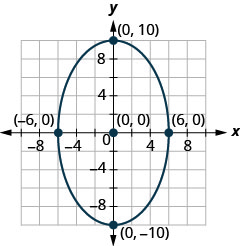
    A figura mostra uma elipse representada graficamente no plano de coordenadas x y. A elipse tem um centro em (0, 0), um eixo maior vertical, vértices em (0, mais ou menos 10) e co-vértices em (mais ou menos 6, 0).
    Figura 11.E.31
    Resposta

    1. \(x^{2}+y^{2}=121\)

    3. \((x+2)^{2}+(y-3)^{2}=52\)

    Exercício\(\PageIndex{25}\)

    Nos exercícios a seguir,

    1. Identifique o tipo de gráfico de cada equação como um círculo, parábola, elipse ou hipérbole e
    2. Faça um gráfico da equação.
    1. \(4 x^{2}+49 y^{2}=196\)
    2. \(y=3(x-2)^{2}-2\)
    3. \(3 x^{2}+3 y^{2}=27\)
    4. \(\frac{y^{2}}{100}-\frac{x^{2}}{36}=1\)
    5. \(\frac{x^{2}}{16}+\frac{y^{2}}{81}=1\)
    6. \(x=2 y^{2}+10 y+7\)
    7. \(64 x^{2}-9 y^{2}=576\)
    Resposta

    1.

    1. Elipse
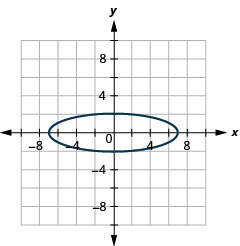
    A figura mostra uma elipse representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 8 a 8. A elipse tem um centro em (0, 0), um eixo maior horizontal, vértices em (mais ou menos 7, 0) e co-vértices em (0, mais ou menos 2).
    Figura 11.E.32

    3.

    1. Círculo
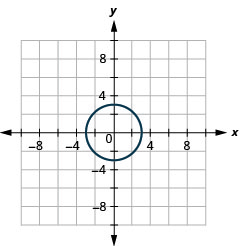
    A figura mostra um círculo representado graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 8 a 8. O círculo da parábola tem um centro em (0, 0) e um raio de 3.
    Figura 11.E.33

    5.

    1. Elipse
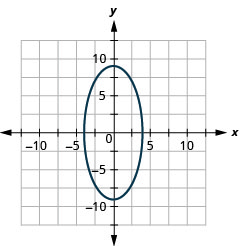
    A figura mostra uma elipse representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 14 a 14. O eixo y do plano vai de menos 10 a 10. A elipse tem um centro em (0, 0), um eixo maior vertical, vértices em (0, mais ou menos 9) e co-vértices em (mais ou menos 4, 0).
    Figura 11.E.34

    7.

    1. Hyperbole
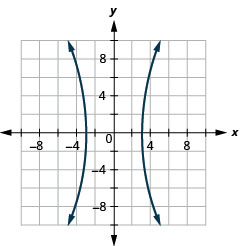
    A figura mostra uma hipérbole representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 8 a 8. A hipérbole tem um centro em (0, 0) e ramificações que passam pelos vértices (mais ou menos 3, 0) e que se abrem para a esquerda e para a direita.
    Figura 11.E.35
    Exercício\(\PageIndex{26}\)

    Nos exercícios a seguir,

    1. Identifique o tipo de gráfico de cada equação como um círculo, parábola, elipse ou hipérbole,
    2. Escreva a equação na forma padrão e
    3. Faça um gráfico da equação.
    1. \(25 x^{2}+64 y^{2}+200 x-256 y-944=0\)
    2. \(x^{2}+y^{2}+10 x+6 y+30=0\)
    3. \(x=-y^{2}+2 y-4\)
    4. \(9 x^{2}-25 y^{2}-36 x-50 y-214=0\)
    5. \(y=x^{2}+6 x+8\)
    6. Resolva o sistema não linear de equações representando graficamente:\(\left\{\begin{array}{l}{3 y^{2}-x=0} \\ {y=-2 x-1}\end{array}\right.\).
    7. Resolva o sistema não linear de equações usando substituição:\(\left\{\begin{array}{l}{x^{2}+y^{2}=8} \\ {y=-x-4}\end{array}\right.\).
    8. Resolva o sistema não linear de equações usando a eliminação:\(\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.\)
    9. Crie a equação do arco parabólico formado na base da ponte mostrada. Dê a resposta em\(y=a x^{2}+b x+c\) forma.
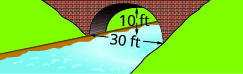
    A figura mostra um arco parabólico formado na base da ponte. O arco tem 10 pés de altura e 30 pés de largura.
    Figura 11.E.36

    10. Um cometa se move em uma órbita elíptica ao redor do sol. O mais próximo que o cometa chega do sol é aproximadamente\(20\) AU e o mais distante é aproximadamente\(70\) AU. O sol é um dos focos da órbita elíptica. Deixando a elipse centrar na origem e rotulando os eixos em AU, a órbita ficará parecida com a figura abaixo. Use o gráfico para escrever uma equação para a órbita elíptica do cometa.

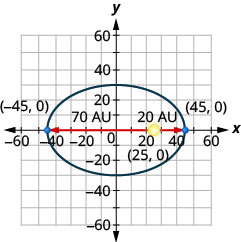
    A figura mostra um modelo de uma órbita elíptica ao redor do sol no plano de coordenadas x y. A elipse tem um centro em (0, 0), um eixo principal horizontal, vértices marcados em (mais ou menos 45, 0), o sol marcado como um foco e rotulado (25, 0), a distância mais próxima que o cometa está do sol marcada como 20 A U e a mais distante um cometa está do sol marcado como 70 A U.
    Figura 11.E.37

    11. A soma de dois números é\(22\) e o produto é\(−240\). Encontre os números.

    12. No aniversário dela, os avós de Olive compraram para ela uma nova TV widescreen. Antes de abri-lo, ela quer ter certeza de que ele se encaixa em seu centro de entretenimento. A TV é\(55\)”. O tamanho de uma TV é medido na diagonal da tela e uma tela widescreen tem um comprimento maior que a largura. A tela também tem uma área de polegadas\(1452\) quadradas. Seu centro de entretenimento tem um encaixe para a TV com um comprimento de\(50\) polegadas e largura de\(40\) polegadas. Quais são o comprimento e a largura da tela da TV e ela se encaixará no centro de entretenimento de Olive?

    Resposta

    2.

    1. Círculo
    2. \((x+5)^{2}+(y+3)^{2}=4\)
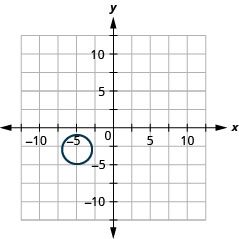
    A figura mostra um círculo representado graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 14 a 14. O eixo y do plano vai de menos 10 a 10. O círculo tem um centro em (menos 5, menos 3) e um raio 2.
    Figura 11.E.38

    4.

    1. Hyperbole
    2. \(\frac{(x-2)^{2}}{25}-\frac{(y+1)^{2}}{9}=1\)
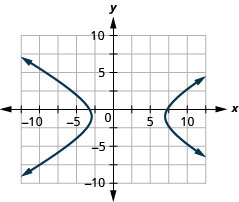
    A figura mostra uma hipérbole representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 14 a 14. O eixo y do plano vai de menos 10 a 10. A hipérbole tem um centro em (2, menos 1) e ramificações que passam pelos vértices (menos 3, menos 1) e (7, menos 1) que se abrem para a esquerda e para a direita.
    Figura 11.E.39

    6. Sem solução

    8. \((0,-3),(0,3)\)

    10. \(\frac{x^{2}}{2025}+\frac{y^{2}}{1400}=1\)

    12. O comprimento é\(44\) polegadas e a largura é\(33\) polegadas. A TV caberá no centro de entretenimento de Olive.

    Glossário

    sistema de equações não lineares
    Um sistema de equações não lineares é um sistema em que pelo menos uma das equações não é linear.