10.5: Use as propriedades dos logaritmos
- Page ID
- 183471
Ao final desta seção, você poderá:
- Use as propriedades dos logaritmos
- Use a fórmula de mudança de base
Antes de começar, faça este teste de prontidão.
- Avalie: a.\(a^{0}\)\(a^{1}\) b.
Se você perdeu esse problema, consulte o Exemplo 5.14. - Escreva com um expoente racional:\(\sqrt[3]{x^{2} y}\).
Se você perdeu esse problema, consulte o Exemplo 8.27. - Arredonde para três casas decimais:\(2.5646415\).
Se você perdeu esse problema, revise o Exemplo 1.34.
Use as propriedades dos logaritmos
Agora que aprendemos sobre funções exponenciais e logarítmicas, podemos introduzir algumas das propriedades dos logaritmos. Isso será muito útil à medida que continuarmos resolvendo equações exponenciais e logarítmicas.
As duas primeiras propriedades derivam da definição de logaritmos. Desde então\(a^{0}=1\), podemos converter isso em forma logarítmica e obter\(\log _{a} 1=0\). Além disso, desde então\(a^{1}=a\), nós recebemos\(\log _{a} a=1\).
Propriedades dos logaritmos
\(\log _{a} 1=0 \quad \log _{a} a=1\)
No próximo exemplo, poderíamos calcular o logaritmo convertendo-o para a forma exponencial, como fizemos anteriormente, mas reconhecer e aplicar as propriedades economiza tempo.
Avalie usando as propriedades dos logaritmos:
- \(\log _{8} 1\)
- \(\log _{6} 6\)
Solução:
uma.
\(\log _{8} 1\)
Use a propriedade,\(\log _{a} 1=0\).
\(0 \quad \log _{8} 1=0\)
b.
\(\log _{6} 6\)
Use a propriedade,\(\log _{a} a=1\).
\(1 \quad \log _{6} 6=1\)
Avalie usando as propriedades dos logaritmos:
- \(\log _{13} 1\)
- \(\log _{9} 9\)
- Resposta
-
- \(0\)
- \(1\)
Avalie usando as propriedades dos logaritmos:
- \(\log _{5} 1\)
- \(\log _{7} 7\)
- Resposta
-
- \(0\)
- \(1\)
As próximas duas propriedades também podem ser verificadas convertendo-as da forma exponencial para a forma logarítmica, ou o contrário.
A equação exponencial é\(a^{\log _{a} x}=x\) convertida para a equação logarítmica\(\log _{a} x=\log _{a} x\), que é uma afirmação verdadeira\(x\) apenas para valores positivos.
A equação logarítmica se\(\log _{a} a^{x}=x\) converte para a equação exponencial\(a^{x}=a^{x}\), que também é uma afirmação verdadeira.
Essas duas propriedades são chamadas de propriedades inversas porque, quando temos a mesma base, elevar a uma potência “desfaz” o tronco e tomar o tronco “desfaz” aumentando para uma potência. Essas duas propriedades mostram a composição das funções. Ambos terminaram com a função de identidade, que mostra novamente que as funções exponenciais e logarítmicas são funções inversas.
Propriedades inversas dos logaritmos
Para\(a>0, x>0\) e\(a \neq 1\),
\(a^{\log _{a} x}=x \quad \log _{a} a^{x}=x\)
No próximo exemplo, aplique as propriedades inversas dos logaritmos.
Avalie usando as propriedades dos logaritmos:
- \(4^{\log _{4} 9}\)
- \(\log _{3} 3^{5}\)
Solução:
uma.
\(4^{\log _{4} 9}\)
Use a propriedade,\(a^{\log _{a} x}=x\).
\(9 \quad 4^{\log _{4} 9}=9\)
b.
\(\log _{3} 3^{5}\)
Use a propriedade,\(a^{\log _{a} x}=x\).
\(5 \quad \log _{3} 3^{5}=5\)
Avalie usando as propriedades dos logaritmos:
- \(5^{\log _{5} 15}\)
- \(\log _{7} 7^{4}\)
- Resposta
-
- \(15\)
- \(4\)
Avalie usando as propriedades dos logaritmos:
- \(2^{\log _{2} 8}\)
- \(\log _{2} 2^{15}\)
- Resposta
-
- \(8\)
- \(15\)
Existem mais três propriedades dos logaritmos que serão úteis em nosso trabalho. Sabemos que as funções exponenciais e logarítmicas estão muito interrelacionadas. Nossa definição de logaritmo nos mostra que um logaritmo é o expoente do exponencial equivalente. As propriedades dos expoentes têm propriedades relacionadas aos expoentes.
Na Propriedade de Produto dos Expoentes\(a^{m} \cdot a^{n}=a^{m+n}\), vemos que, para multiplicar a mesma base, adicionamos os expoentes. A propriedade do produto dos logaritmos, nos\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\) diz para pegar o registro de um produto, adicionamos o log dos fatores.
Propriedade do produto dos logaritmos
Se\(M>0, N>0, \mathrm{a}>0\) e\(\mathrm{a} \neq 1,\) depois
\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\)
O logaritmo de um produto é a soma dos logaritmos.
Usamos essa propriedade para escrever o log de um produto como uma soma dos registros de cada fator.
Use a propriedade de produto dos logaritmos para escrever cada logaritmo como uma soma dos logaritmos. Simplifique, se possível:
- \(\log _{3} 7 x\)
- \(\log _{4} 64 x y\)
Solução:
uma.
\(\log _{3} 7 x\)
Use a propriedade do produto,\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\).
\(\log _{3} 7+\log _{3} x\)
\(\log _{3} 7 x=\log _{3} 7+\log _{3} x\)
b.
\(\log _{4} 64 x y\)
Use a propriedade do produto,\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\).
\(\log _{4} 64+\log _{4} x+\log _{4} y\)
Simplifique a avaliação,\(\log _{4} 64\).
\(3+\log _{4} x+\log _{4} y\)
\(\log _{4} 64 x y=3+\log _{4} x+\log _{4} y\)
Use a propriedade de produto dos logaritmos para escrever cada logaritmo como uma soma dos logaritmos. Simplifique, se possível:
- \(\log _{3} 3 x\)
- \(\log _{2} 8 x y\)
- Resposta
-
- \(1+\log _{3} x\)
- \(3+\log _{2} x+\log _{2} y\)
Use a propriedade de produto dos logaritmos para escrever cada logaritmo como uma soma dos logaritmos. Simplifique, se possível:
- \(\log _{9} 9 x\)
- \(\log _{3} 27 x y\)
- Resposta
-
- \(1+\log _{9} x\)
- \(3+\log _{3} x+\log _{3} y\)
Da mesma forma, na Propriedade Quociente dos Expoentes\(\frac{a^{m}}{a^{n}}=a^{m-n}\), vemos que, para dividir a mesma base, subtraímos os expoentes. A propriedade quociente dos logaritmos, nos\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\) diz que, para pegar o log de um quociente, subtraímos o log do numerador e do denominador.
Propriedade quociente dos logaritmos
Se\(M>0, N>0, \mathrm{a}>0\) e\(\mathrm{a} \neq 1,\) depois
\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\)
O logaritmo de um quociente é a diferença dos logaritmos.
Observe isso\(\log _{a} M=\log _{a} N \not=\log _{a}(M-N)\).
Usamos essa propriedade para escrever o log de um quociente como uma diferença dos registros de cada fator.
Use a propriedade quociente dos logaritmos para escrever cada logaritmo como uma diferença de logaritmos. Simplifique, se possível.
- \(\log _{5} \frac{5}{7}\)
- \(\log \frac{x}{100}\)
Solução:
uma.
\(\log _{5} \frac{5}{7}\)
Use a propriedade do quociente,\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\).
\(\log _{5} 5-\log _{5} 7\)
Simplifique.
\(1-\log _{5} 7\)
\(\log _{5} \frac{5}{7}=1-\log _{5} 7\)
b.
\(\log \frac{x}{100}\)
Use a propriedade do quociente,\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\).
\(\log x-\log 100\)
Simplifique.
\(\log x-2\)
\(\log \frac{x}{100}=\log x-2\)
Use a propriedade quociente dos logaritmos para escrever cada logaritmo como uma diferença de logaritmos. Simplifique, se possível.
- \(\log _{4} \frac{3}{4}\)
- \(\log \frac{x}{1000}\)
- Resposta
-
- \(\log _{4} 3-1\)
- \(\log x-3\)
Use a propriedade quociente dos logaritmos para escrever cada logaritmo como uma diferença de logaritmos. Simplifique, se possível.
- \(\log _{2} \frac{5}{4}\)
- \(\log \frac{10}{y}\)
- Resposta
-
- \(\log _{2} 5-2\)
- \(1-\log y\)
A terceira propriedade dos logaritmos está relacionada à propriedade de potência dos expoentes\(\left(a^{m}\right)^{n}=a^{m \cdot n}\), vemos que, para elevar uma potência a uma potência, multiplicamos os expoentes. A propriedade de potência dos logaritmos, nos\(\log _{a} M^{p}=p \log _{a} M\) diz que, para pegar o log de um número elevado a uma potência, multiplicamos a potência pelo log do número.
Propriedade de poder dos logaritmos
Se\(M>0, \mathrm{a}>0, \mathrm{a} \neq 1\) e\(p\) for qualquer número real, então,
\(\log _{a} M^{p}=p \log _{a} M\)
O registro de um número elevado a uma potência como o produto da potência multiplicado pelo log do número.
Usamos essa propriedade para escrever o log de um número elevado a uma potência como o produto da potência multiplicado pelo log do número. Basicamente, pegamos o expoente e o jogamos na frente do logaritmo.
Use a propriedade de potência dos logaritmos para escrever cada logaritmo como um produto dos logaritmos. Simplifique, se possível.
- \(\log _{5} 4^{3}\)
- \(\log x^{10}\)
Solução:
uma.
\(\log _{5} 4^{3}\)
Use a propriedade Power,\(\log _{a} M^{p}=p \log _{a} M\).
3\(\log _{5} 4\)
\(\log _{5} 4^{3}=3 \log _{5} 4\)
b.
\(\log x^{10}\)
Use a propriedade Power,\(\log _{a} M^{p}=p \log _{a} M\).
\(10\log x\)
\(\log x^{10}=10 \log x\)
Use a propriedade de potência dos logaritmos para escrever cada logaritmo como um produto dos logaritmos. Simplifique, se possível.
- \(\log _{7} 5^{4}\)
- \(\log x^{100}\)
- Resposta
-
- \(4\log _{7} 5\)
- 100\(\cdot \log x\)
Use a propriedade de potência dos logaritmos para escrever cada logaritmo como um produto dos logaritmos. Simplifique, se possível.
- \(\log _{2} 3^{7}\)
- \(\log x^{20}\)
- Resposta
-
- \(7\log _{2} 3\)
- \(20\cdot \log x\)
Resumimos as propriedades dos logaritmos aqui para facilitar a referência. Embora os logaritmos naturais sejam um caso especial dessas propriedades, geralmente é útil mostrar também a versão do logaritmo natural de cada propriedade.
Propriedades dos logaritmos
Se\(M>0, \mathrm{a}>0, \mathrm{a} \neq 1\) e\(p\) for qualquer número real, então,
| Propriedade | Base\(a\) | Base\(e\) |
|---|---|---|
| \ (a\) ">\(\log _{a} 1=0\) | \ (e\) ">\(\ln 1=0\) | |
| \ (a\) ">\(\log _{a} a=1\) | \ (e\) ">\(\ln e=1\) | |
| Propriedades inversas | \ (a\) ">\(a^{\log _{a} x}=x\) \(\log _{a} a^{x}=x\) |
\ (e\) ">\(e^{\ln x}=x\) \(\ln e^{x}=x\) |
| Propriedade do produto dos logaritmos | \ (a\) ">\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\) | \ (e\) ">\(\ln (M \cdot N)=\ln M+\ln N\) |
| Propriedade quociente dos logaritmos | \ (a\) ">\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\) | \ (e\) ">\(\ln \frac{M}{N}=\ln M-\ln N\) |
| Propriedade de poder dos logaritmos | \ (a\) ">\(\log _{a} M^{p}=p \log _{a} M\) | \ (e\) ">\(\ln M^{p}=p \ln M\) |
Agora que temos as propriedades, podemos usá-las para “expandir” uma expressão logarítmica. Isso significa escrever o logaritmo como uma soma ou diferença e sem nenhum poder.
Geralmente aplicamos as propriedades do produto e do quociente antes de aplicarmos a propriedade de energia.
Use as propriedades dos logaritmos para expandir o logaritmo\(\log _{4}\left(2 x^{3} y^{2}\right)\). Simplifique, se possível.
Solução:
Use a propriedade do produto,\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\).
Use a propriedade de poder\(\log _{a} M^{p}=p \log _{a} M\),, nos dois últimos termos. Simplifique.
Use as propriedades dos logaritmos para expandir o logaritmo\(\log _{2}\left(5 x^{4} y^{2}\right)\). Simplifique, se possível.
- Resposta
-
\(\log _{2} 5+4 \log _{2} x+2 \log _{2} y\)
Use as propriedades dos logaritmos para expandir o logaritmo\(\log _{3}\left(7 x^{5} y^{3}\right)\). Simplifique, se possível.
- Resposta
-
\(\log _{3} 7+5 \log _{3} x+3 \log _{3} y\)
Quando temos um radical na expressão logarítmica, é útil primeiro escrever seu radicando como um expoente racional.
Use as propriedades dos logaritmos para expandir o logaritmo\(\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}\). Simplifique, se possível.
Solução
\(\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}\)
Reescreva o radical com um expoente racional.
\(\log _{2}\left(\frac{x^{3}}{3 y^{2} z}\right)^{\frac{1}{4}}\)
Use a propriedade Power,\(\log _{a} M^{p}=p \log _{a} M\).
\(\frac{1}{4} \log _{2}\left(\frac{x^{3}}{3 y^{2} z}\right)\)
Use a propriedade do quociente,\(\log _{a} M \cdot N=\log _{a} M-\log _{a} N\).
\(\frac{1}{4}\left(\log _{2}\left(x^{3}\right)-\log _{2}\left(3 y^{2} z\right)\right)\)
Use a Propriedade do Produto\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\),, no segundo termo.
\(\frac{1}{4}\left(\log _{2}\left(x^{3}\right)-\left(\log _{2} 3+\log _{2} y^{2}+\log _{2} z\right)\right)\)
Use a propriedade de poder\(\log _{a} M^{p}=p \log _{a} M\),, dentro dos parênteses.
\(\frac{1}{4}\left(3 \log _{2} x-\left(\log _{2} 3+2 \log _{2} y+\log _{2} z\right)\right)\)
Simplifique distribuindo.
\(\frac{1}{4}\left(3 \log _{2} x-\log _{2} 3-2 \log _{2} y-\log _{2} z\right)\)
\(\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}=\frac{1}{4}\left(3 \log _{2} x-\log _{2} 3-2 \log _{2} y-\log _{2} z\right)\)
Use as propriedades dos logaritmos para expandir o logaritmo\(\log _{4} \sqrt[5]{\frac{x^{4}}{2 y^{3} z^{2}}}\). Simplifique, se possível.
- Resposta
-
\(\frac{1}{5}\left(4 \log _{4} x-\frac{1}{2}-3 \log _{4} y-2 \log _{4} z\right)\)
Use as propriedades dos logaritmos para expandir o logaritmo\(\log _{3} \sqrt[3]{\frac{x^{2}}{5 y z}}\). Simplifique, se possível.
- Resposta
-
\(\frac{1}{3}\left(2 \log _{3} x-\log _{3} 5-\log _{3} y-\log _{3} z\right)\)
O oposto de expandir um logaritmo é condensar uma soma ou diferença de logaritmos que têm a mesma base em um único logaritmo. Mais uma vez, usamos as propriedades dos logaritmos para nos ajudar, mas ao contrário.
Para condensar expressões logarítmicas com a mesma base em um logaritmo, começamos usando a Propriedade de Potência para obter os coeficientes dos termos logarítmicos como um e, em seguida, as Propriedades do Produto e do Quociente, conforme necessário.
Use as propriedades dos logaritmos para condensar o logaritmo\(\log _{4} 3+\log _{4} x-\log _{4} y\). Simplifique, se possível.
Solução:
Todas as expressões de log têm a mesma base,\(4\).
Os dois primeiros termos são adicionados, então usamos a Propriedade do Produto,\(\log _{a} M+\log _{a} N=\log _{a} M : N\).
Como os registros são subtraídos, usamos a propriedade do quociente,\(\log _{a} M-\log _{a} N=\log _{a} \frac{M}{N}\).
Use as propriedades dos logaritmos para condensar o logaritmo\(\log _{2} 5+\log _{2} x-\log _{2} y\). Simplifique, se possível.
- Resposta
-
\(\log _{2} \frac{5 x}{y}\)
Use as propriedades dos logaritmos para condensar o logaritmo\(\log _{3} 6-\log _{3} x-\log _{3} y\). Simplifique, se possível.
- Resposta
-
\(\log _{3} \frac{6}{x y}\)
Use as propriedades dos logaritmos para condensar o logaritmo\(2 \log _{3} x+4 \log _{3}(x+1)\). Simplifique, se possível.
Solução:
As expressões de log têm a mesma base,\(3\).
\(2 \log _{3} x+4 \log _{3}(x+1)\)
Use a propriedade Power,\(\log _{a} M+\log _{a} N=\log _{a} M \cdot N\).
\(\log _{3} x^{2}+\log _{3}(x+1)^{4}\)
Os termos são adicionados, então usamos a Propriedade do Produto,\(\log _{a} M+\log _{a} N=\log _{a} M \cdot N\).
\(\log _{3} x^{2}(x+1)^{4}\)
\(2 \log _{3} x+4 \log _{3}(x+1)=\log _{3} x^{2}(x+1)^{4}\)
Use as propriedades dos logaritmos para condensar o logaritmo\(3 \log _{2} x+2 \log _{2}(x-1)\). Simplifique, se possível.
- Resposta
-
\(\log _{2} x^{3}(x-1)^{2}\)
Use as propriedades dos logaritmos para condensar o logaritmo\(2 \log x+2 \log (x+1)\). Simplifique, se possível.
- Resposta
-
\(\log x^{2}(x+1)^{2}\)
Use a fórmula de mudança de base
Para calcular um logaritmo com qualquer outra base, podemos usar a Fórmula de Mudança de Base. Mostraremos como isso é derivado.
\(\begin{array} {l c} {\text{Suppose we want to evaluate} \log_{a}M} & {\log_{a}M} \\ {\text{Let} \:y =\log_{a}M. }&{y=\log_{a}M} \\ {\text{Rewrite the epression in exponential form. }}&{a^{y}=M } \\ {\text{Take the }\:\log_{b} \text{of each side.}}&{\log_{b}a^{y}=\log_{b}M}\\ {\text{Use the Power Property.}}&{y\log_{b}a=\log_{b}M} \\ {\text{Solve for}\:y. }&{y=\frac{\log_{b}M}{\log_{b}a}} \\ {\text{Substiture}\:y=\log_{a}M.}&{\log_{a}M=\frac{\log_{b}M}{\log_{b}a}} \end{array}\)
A fórmula de mudança de base introduz uma nova base\(b\). Essa pode ser qualquer base\(b\) que quisermos e onde quisermos\(b>0,b≠1\). Como nossas calculadoras têm chaves para logaritmos base\(10\) e base\(e\), reescreveremos a Fórmula de Mudança de Base com a nova base como\(10\) ou\(e\).
Fórmula de mudança de base
Para quaisquer bases logarítmicas\(a, b\) e\(M>0\),
\(\begin{array}{lll}{\log _{a} M=\frac{\log _{b} M}{\log _{b} a}} & {\log _{a} M=\frac{\log M}{\log a}} & {\log _{a} M=\frac{\ln M}{\ln a}} \\ {\text { new base } b} & {\text { new base } 10} & {\text { new base } e}\end{array}\)
Quando usamos uma calculadora para encontrar o valor do logaritmo, geralmente arredondamos para três casas decimais. Isso nos dá um valor aproximado e, portanto, usamos o símbolo aproximadamente igual\((≈)\).
Arredondamento para três casas decimais, aproximado\(\log _{4} 35\).
Solução:
 |
|
| Use a fórmula de mudança de base. | 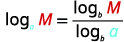 |
| Identifique\(a\)\(M\) e. Escolha\(10\) por\(b\). | 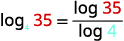 |
| Insira a expressão\(\frac{\log 35}{\log 4}\) na calculadora usando o botão de registro como base\(10\). Arredonde para três casas decimais. | 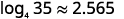 |
Arredondamento para três casas decimais, aproximado\(\log _{3} 42\).
- Resposta
-
\(3.402\)
Arredondamento para três casas decimais, aproximado\(\log _{5} 46\).
- Resposta
-
\(2.379\)
Acesse esses recursos on-line para obter instruções adicionais e praticar o uso das propriedades dos logaritmos.
Conceitos chave
- \(\log _{a} 1=0 \quad \log _{a} a=1\)
- Propriedades inversas dos logaritmos
- Para\(a>0,x>0\) e\(a≠1\)
\(a^{\log _{a} x}=x \quad \log _{a} a^{x}=x\)
- Para\(a>0,x>0\) e\(a≠1\)
- Propriedade do produto dos logaritmos
- Se\(M>0,N>0,a>0\) e\(a≠1\), então,
\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\)
O logaritmo de um produto é a soma dos logaritmos.
- Se\(M>0,N>0,a>0\) e\(a≠1\), então,
- Propriedade quociente dos logaritmos
- Se\(M>0, N>0, \mathrm{a}>0\) e\(a≠1\), então,
\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\)
O logaritmo de um quociente é a diferença dos logaritmos.
- Se\(M>0, N>0, \mathrm{a}>0\) e\(a≠1\), então,
- Propriedade de poder dos logaritmos
- Se\(M>0,a>0,a≠1\) e\(p\) for qualquer número real, então,
\(\log _{a} M^{p}=p \log _{a} M\)
O registro de um número elevado a uma potência é o produto da potência vezes o log do número.
- Se\(M>0,a>0,a≠1\) e\(p\) for qualquer número real, então,
- Resumo das propriedades dos logaritmos
Se\(M>0,a>0,a≠1\) e\(p\) for qualquer número real, então,
| Propriedade | Base\(a\) | Base\(e\) |
|---|---|---|
| \ (a\) ">\(\log _{a} 1=0\) | \ (e\) ">\(\ln 1=0\) | |
| \ (a\) ">\(\log _{a} a=1\) | \ (e\) ">\(\ln e=1\) | |
| Propriedades inversas | \ (a\) ">\(a^{\log _{a} x}=x\) \(\log _{a} a^{x}=x\) |
\ (e\) ">\(e^{\ln x}=x\) \(\ln e^{x}=x\) |
| Propriedade do produto dos logaritmos | \ (a\) ">\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\) | \ (e\) ">\(\ln (M \cdot N)=\ln M+\ln N\) |
| Propriedade quociente dos logaritmos | \ (a\) ">\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\) | \ (e\) ">\(\ln \frac{M}{N}=\ln M-\ln N\) |
| Propriedade de poder dos logaritmos | \ (a\) ">\(\log _{a} M^{p}=p \log _{a} M\) | \ (e\) ">\(\ln M^{p}=p \ln M\) |
- Fórmula de mudança de base
Para quaisquer bases logarítmicas\(a\) e\(b\), e\(M>0\),\(\begin{array}{ll}{\log _{a} M=\frac{\log _{b} M}{\log _{b} a}} & {\log _{a} M=\frac{\log M}{\log a}} & {\log _{a} M=\frac{\ln M}{\ln a}} \\ {\text { new base } b} & {\text { new base } 10} & {\text { new base } e}\end{array}\)


