10.4: Avalie e represente graficamente funções logarítmicas
- Page ID
- 183493
Ao final desta seção, você poderá:
- Converta entre a forma exponencial e logarítmica
- Avalie funções logarítmicas
- Grafar funções logarítmicas
- Resolva equações logarítmicas
- Use modelos logarítmicos em aplicativos
Antes de começar, faça este teste de prontidão.
- Resolver:\(x^{2}=81\).
Se você perdeu esse problema, revise o Exemplo 6.46. - Avalie:\(3^{−2}\).
Se você perdeu esse problema, consulte o Exemplo 5.15. - Resolver:\(2^{4}=3x−5\).
Se você perdeu esse problema, revise o Exemplo 2.2.
Passamos algum tempo encontrando o inverso de muitas funções. Funciona bem para “desfazer” uma operação com outra operação. Subtrair 'desfaz' adição, multiplicação 'desfaz' divisão, tomando a raiz quadrada 'desfaz' ao quadrado.
Ao estudarmos a função exponencial, vimos que ela é individual, pois seus gráficos passam no teste da linha horizontal. Isso significa que uma função exponencial tem um inverso. Se tentarmos nosso método algébrico para encontrar um inverso, nos deparamos com um problema.
\(f(x)=a^{x}\)
Reescreva com\(y=f(x)\).
\(y=a^{x}\)
Troque as variáveis\(x\)\(y\) e.
\(x=a^{y}\)
Resolver para\(y\).
Opa! Não temos como resolver\(y\)!
Para lidar com isso, definimos a função logarítmica com base a como sendo o inverso da função exponencial\(f(x)=a^{x}\). Usamos a notação\(f^{−1}(x)=log_{a}x\) e dizemos que a função inversa da função exponencial é a função logarítmica.
A função\(f(x)=\log_{a}x\) é a função logarítmica com base\(a\)\(a>0,x>0\), onde,\(a≠1\) e.
\(y=\log _{a} x\)é equivalente a\(x=a^{y}\)
Converter entre a forma exponencial e logarítmica
Como as equações\(y=\log _{a} x\)\(x=a^{y}\) são equivalentes, podemos ir e voltar entre elas. Esse geralmente será o método para resolver algumas equações exponenciais e logarítmicas. Para ajudar na conversão para frente e para trás, vamos dar uma olhada nas equações. Veja a Figura 10.3.1. Observe as posições do expoente e da base.
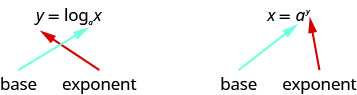
Se percebermos que o logaritmo é o expoente, isso facilita a conversão. Você pode repetir: “com base no expoente, forneça o número”.
Converter para a forma logarítmica:
- \(2^{3}=8\)
- \(5^{\frac{1}{2}}=\sqrt{5}\)
- \(\left(\frac{1}{2}\right)^{x}=\frac{1}{16}\)
Solução:
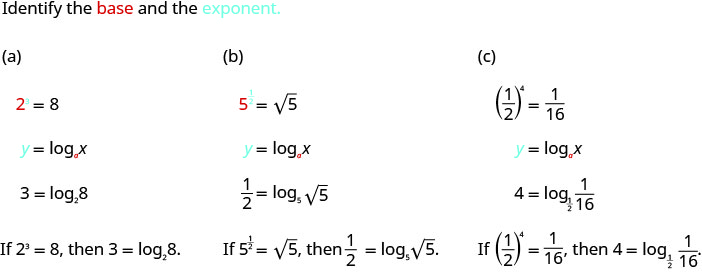
Converter para a forma logarítmica:
- \(3^{2}=9\)
- \(7^{\frac{1}{2}}=\sqrt{7}\)
- \(\left(\frac{1}{3}\right)^{x}=\frac{1}{27}\)
- Responda
-
- \(\log _{3} 9=2\)
- \(\log _{7} \sqrt{7}=\frac{1}{2}\)
- \(\log _{\frac{1}{3}} \frac{1}{27}=x\)
Converter para a forma logarítmica:
- \(4^{3}=64\)
- \(4^{\frac{1}{3}}=\sqrt[3]{4}\)
- \(\left(\frac{1}{2}\right)^{x}=\frac{1}{32}\)
- Responda
-
- \(\log _{4} 64=3\)
- \(\log _{4} \sqrt[3]{4}=\frac{1}{3}\)
- \(\log _{\frac{1}{2}} \frac{1}{32}=x\)
No próximo exemplo, fazemos a conversão inversa da forma logarítmica para a forma exponencial.
Converta para a forma exponencial:
- \(2=\log _{8} 64\)
- \(0=\log _{4} 1\)
- \(-3=\log _{10} \frac{1}{1000}\)
Solução:
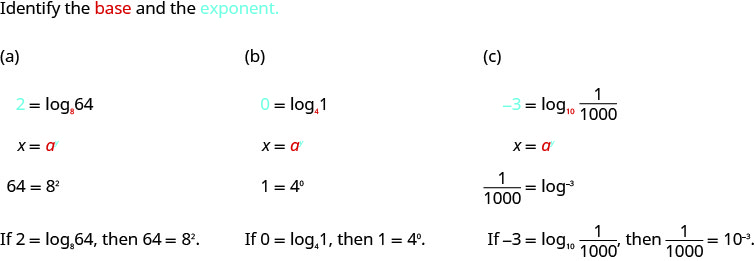
Converta para a forma exponencial:
- \(3=\log _{4} 64\)
- \(0=\log _{x} 1\)
- \(-2=\log _{10} \frac{1}{100}\)
- Responda
-
- \(64=4^{3}\)
- \(1=x^{0}\)
- \(\frac{1}{100}=10^{-2}\)
Converta para a forma exponencial:
- \(3=\log _{3} 27\)
- \(0=\log _{x} 1\)
- \(-1=\log _{10} \frac{1}{10}\)
- Responda
-
- \(27=3^{3}\)
- \(1=x^{0}\)
- \(\frac{1}{10}=10^{-1}\)
Avalie funções logarítmicas
Podemos resolver e avaliar equações logarítmicas usando a técnica de converter a equação em sua equação exponencial equivalente.
Encontre o valor de\(x\):
- \(\log _{x} 36=2\)
- \(\log _{4} x=3\)
- \(\log _{\frac{1}{2}} \frac{1}{8}=x\)
Solução:
uma.
\(\log _{x} 36=2\)
Converta para a forma exponencial.
\(x^{2}=36\)
Resolva a quadrática.
\(x=6, \quad \cancel{x=-6}\)
A base de uma função logarítmica deve ser positiva, então eliminamos\(x=−6\).
\(x=6 \quad\)Portanto,\(\log _{6} 36=2\)
b.
\(\log _{4} x=3\)
Converta para a forma exponencial.
\(4^{3}=x\)
Simplifique.
\(x=64 \quad\)Portanto\(, \log _{4} 64=3\)
c.
\(\log _{\frac{1}{2}} \frac{1}{8}=x\)
Converta para a forma exponencial.
\(\left(\frac{1}{2}\right)^{x}=\frac{1}{8}\)
Reescreva\(\frac{1}{8}\) como\(\left(\frac{1}{2}\right)^{3}\).
\(\left(\frac{1}{2}\right)^{x}=\left(\frac{1}{2}\right)^{3}\)
Com a mesma base, os expoentes devem ser iguais.
\(x=3 \quad\)Portanto\(\log _{\frac{1}{2}} \frac{1}{8}=3\)
Encontre o valor de\(x\):
- \(\log _{x} 64=2\)
- \(\log _{5} x=3\)
- \(\log _{\frac{1}{2}} \frac{1}{4}=x\)
- Responda
-
- \(x=8\)
- \(x=125\)
- \(x=2\)
Encontre o valor de\(x\):
- \(\log _{x} 81=2\)
- \(\log _{3} x=5\)
- \(\log _{\frac{1}{3}} \frac{1}{27}=x\)
- Responda
-
- \(x=9\)
- \(x=243\)
- \(x=3\)
Quando vemos uma expressão como\(log_{3}27\), podemos encontrar seu valor exato de duas maneiras. Por inspeção, percebemos que significa “\(3\)para que poder será\(27\)”? Desde então\(3^{3}=27\), nós sabemos\(log_{3}27=3\). Uma forma alternativa é definir a expressão igual a\(x\) e depois convertê-la em uma equação exponencial.
Encontre o valor exato de cada logaritmo sem usar uma calculadora:
- \(\log _{5} 25\)
- \(\log _{9} 3\)
- \(\log _{2} \frac{1}{16}\)
Solução:
uma.
\(\log _{5} 25\)
\(5\)para que poder será\(25\)?
\(\log _{5} 25=2\)
Ou
Defina a expressão igual\(x\) a.
\(\log _{5} 25=x\)
Mude para a forma exponencial.
\(5^{x}=25\)
Reescreva\(25\) como\(5^{2}\).
\(5^{x}=5^{2}\)
Com a mesma base, os expoentes devem ser iguais.
\(x=2 \quad\)Portanto\(, \log _{5} 25=2\).
b.
\(\log _{9} 3\)
Defina a expressão igual\(x\) a.
\(\log _{9} 3=x\)
Mude para a forma exponencial.
\(9^{x}=3\)
Reescreva\(9\) como\(3^{2}\).
\(\left(3^{2}\right)^{x}=3^{1}\)
Simplifique os expoentes.
\(3^{2 x}=3^{1}\)
Com a mesma base, os expoentes devem ser iguais.
\(2 x=1\)
Resolva a equação.
\(x=\frac{1}{2} \quad\)Portanto\(, \log _{9} 3=\frac{1}{2}\).
c.
\(\log _{2} \frac{1}{16}\)
Defina a expressão igual\(x\) a.
\(\log _{2} \frac{1}{16}=x\)
Mude para a forma exponencial.
\(2^{x}=\frac{1}{16}\)
Reescreva\(16\) como\(2^{4}\).
\(2^{x}=\frac{1}{2^{4}}\)
\(2^{x}=2^{-4}\)
Com a mesma base, os expoentes devem ser iguais.
\(x=-4 \quad\)Portanto\(, \log _{2} \frac{1}{16}=-4\).
Encontre o valor exato de cada logaritmo sem usar uma calculadora:
- \(\log _{12} 144\)
- \(\log _{4} 2\)
- \(\log _{2} \frac{1}{32}\)
- Responda
-
- \(2\)
- \(\frac{1}{2}\)
- \(-5\)
Encontre o valor exato de cada logaritmo sem usar uma calculadora:
- \(\log _{9} 81\)
- \(\log _{8} 2\)
- \(\log _{3} \frac{1}{9}\)
- Responda
-
- \(2\)
- \(\frac{1}{3}\)
- \(-2\)
Grafe funções logarítmicas
Para representar graficamente uma função logarítmica\(y=log_{a}x\), é mais fácil converter a equação em sua forma exponencial,\(x=a^{y}\). Geralmente, quando procuramos pares ordenados para o gráfico de uma função, geralmente escolhemos um\(x\) valor -e, em seguida, determinamos seu\(y\) valor -correspondente. Nesse caso, você pode achar mais fácil escolher\(y\) -values e, em seguida, determinar o\(x\) valor -correspondente.
Gráfico\(y=\log _{2} x\).
Solução:
Para representar graficamente a função, primeiro reescreveremos a equação logarítmica\(y=\log _{2} x\),, na forma exponencial,\(2^{y}=x\).
Usaremos a plotagem de pontos para representar graficamente a função. Será mais fácil começar com valores de\(y\) e depois obter\(x\).
| \(y\) | \(2^{y}=x\) | \((x,y)\) |
|---|---|---|
| \ (y\) ">\(-2\) | \ (2^ {y} =x\) ">\(2^{-2}=\frac{1}{2^{2}}=\frac{1}{4}\) | \ ((x, y)\) ">\((\frac{1}{4},2)\) |
| \ (y\) ">\(-1\) | \ (2^ {y} =x\) ">\(2^{-1}=\frac{1}{2^{1}}=\frac{1}{2}\) | \ ((x, y)\) ">\((\frac{1}{2},-1)\) |
| \ (y\) ">\(0\) | \ (2^ {y} =x\) ">\(2^{0}=1\) | \ ((x, y)\) ">\((1,0)\) |
| \ (y\) ">\(1\) | \ (2^ {y} =x\) ">\(2^{1}=2\) | \ ((x, y)\) ">\((2,1)\) |
| \ (y\) ">\(2\) | \ (2^ {y} =x\) ">\(2^{2}=4\) | \ ((x, y)\) ">\((4,2)\) |
| \ (y\) ">\(3\) | \ (2^ {y} =x\) ">\(2^{3}=8\) | \ ((x, y)\) ">\((8,3)\) |
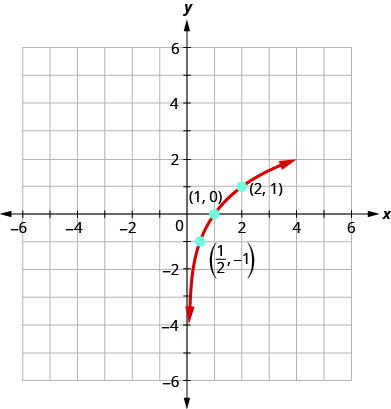
Gráfico:\(y=\log _{3} x\).
- Responda
-
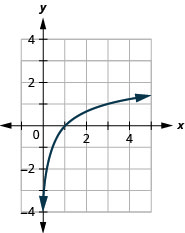
Figura 10.3.5
Gráfico:\(y=\log _{5} x\).
- Responda
-
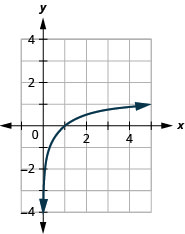
Figura 10.3.6
Os gráficos de\(y=\log _{2} x, y=\log _{3} x\), e\(y=\log _{5} x\) são a forma que esperamos de uma função logarítmica onde\(a>1\).
Percebemos que, para cada função, o gráfico contém o ponto\((1,0)\). Isso faz sentido porque\(0=log_{a}1\) significa\(a^{0}=1\) que é verdadeiro para qualquer um\(a\).
O gráfico de cada função também contém o ponto\((a,1)\). Isso faz sentido como\(1=\log _{a} a\) meio\(a^{1}=a\). O que é verdade para qualquer um\(a\).
Observe também que o gráfico de cada função\(y=\log _{a} x\) também contém o ponto\(\left(\frac{1}{a},-1\right)\). Isso faz sentido como\(-1=\log _{a} \frac{1}{a}\) meio\(a^{-1}=\frac{1}{a}\), o que vale para qualquer um\(a\).
Veja cada gráfico novamente. Agora veremos que muitas características da função logarítmica são simplesmente “imagens espelhadas” das características da função exponencial correspondente.
Qual é o domínio da função? O gráfico nunca atinge o\(y\) eixo -. O domínio contém todos números positivos. Escrevemos o domínio em notação de intervalo como\((0,∞)\).
Qual é o alcance de cada função? A partir dos gráficos, podemos ver que o intervalo é o conjunto de todos os números reais. Não há restrição no alcance. Escrevemos o intervalo em notação de intervalo como\((−∞,∞)\).
Quando o gráfico se aproxima do\(y\) eixo -tão de perto, mas nunca o cruza, chamamos a linha\(x=0\) de\(y\) eixo -de assíntota vertical.
| Domínio | \((0, \infty)\) |
| Alcance | \((-\infty, \infty)\) |
| \(x\)-interceptar | \((1,0)\) |
| \(y\)-interceptar | Nenhuma |
| Contém | \((a, 1),\left(\frac{1}{a},-1\right)\) |
| Assíntota | \(y\)-eixo |
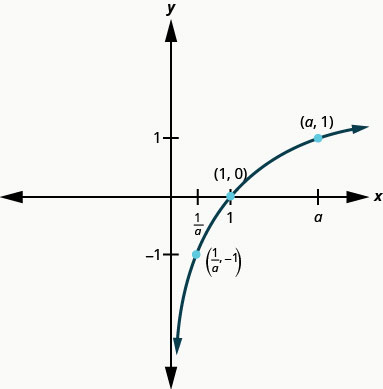
Nosso próximo exemplo analisa o gráfico de\(y=log_{a}x\) quando\(0<a<1\).
Gráfico\(y=\log _{\frac{1}{3}} x\).
Solução:
Para representar graficamente a função, primeiro reescreveremos a equação logarítmica\(y=\log _{\frac{1}{3}} x\),, na forma exponencial,\(\left(\frac{1}{3}\right)^{y}=x\).
Usaremos a plotagem de pontos para representar graficamente a função. Será mais fácil começar com valores de\(y\) e depois obter\(x\).
| \(y\) | \(\left(\frac{1}{3}\right)^{y}=x\) | \((x,y)\) |
|---|---|---|
| \ (y\) ">\(-2\) | \ (\ left (\ frac {1} {3}\ direita) ^ {y} =x\) ">\(\left(\frac{1}{3}\right)^{-2}=3^{2}=9\) | \ ((x, y)\) ">\((9,-2)\) |
| \ (y\) ">\(-1\) | \ (\ left (\ frac {1} {3}\ direita) ^ {y} =x\) ">\(\left(\frac{1}{3}\right)^{-1}=3^{1}=3\) | \ ((x, y)\) ">\((3,-1)\) |
| \ (y\) ">\(0\) | \ (\ left (\ frac {1} {3}\ direita) ^ {y} =x\) ">\(\left(\frac{1}{3}\right)^{0}=1\) | \ ((x, y)\) ">\((1,0)\) |
| \ (y\) ">\(1\) | \ (\ left (\ frac {1} {3}\ direita) ^ {y} =x\) ">\(\left(\frac{1}{3}\right)^{1}=\frac{1}{3}\) | \ ((x, y)\) ">\(\left(\frac{1}{3}, 1\right)\) |
| \ (y\) ">\(2\) | \ (\ left (\ frac {1} {3}\ direita) ^ {y} =x\) ">\(\left(\frac{1}{3}\right)^{2}=\frac{1}{9}\) | \ ((x, y)\) ">\(\left(\frac{1}{9}, 2\right)\) |
| \ (y\) ">\(3\) | \ (\ left (\ frac {1} {3}\ direita) ^ {y} =x\) ">\(\left(\frac{1}{3}\right)^{3}=\frac{1}{27}\) | \ ((x, y)\) ">\(\left(\frac{1}{27}, 3\right)\) |
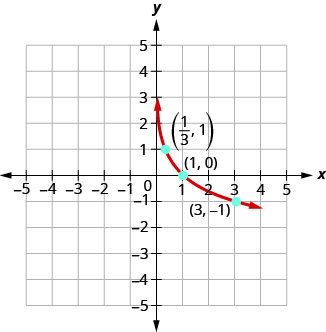
Gráfico:\(y=\log _{\frac{1}{2}} x\).
- Responda
-
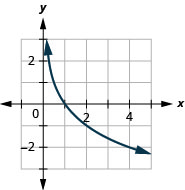
Gráfico:\(y=\log _{\frac{1}{4}} x\).
- Responda
-
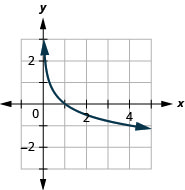
Agora, vamos dar uma olhada nos gráficos\(y=\log _{\frac{1}{2}} x, y=\log _{\frac{1}{3}} x\) e\(y=\log _{\frac{1}{4}} x\), para que possamos identificar algumas das propriedades das funções logarítmicas onde\(0<a<1\).
Os gráficos de todos têm a mesma forma básica. Embora essa seja a forma que esperamos de uma função logarítmica onde\(0<a<1\).
Percebemos que, para cada função, novamente, o gráfico contém os pontos,\((1,0),(a, 1),\left(\frac{1}{a},-1\right)\). Isso faz sentido pelos mesmos motivos que discutimos acima.
Percebemos que o domínio e o intervalo também são os mesmos — o domínio é\((0,∞)\) e o intervalo são\((−∞,∞)\). O\(y\) eixo -é novamente a assíntota vertical.
Resumiremos essas propriedades no gráfico abaixo. O que também inclui quando\(a>1\).
| Quando\(a>1\) | Quando\(0<a<1\) | ||
|---|---|---|---|
| \ (a">1\) ">Domínio | \((0, \infty)\) | \ (0<a<1\) ">Domínio | \((0, \infty)\) |
| \ (a">1\) ">Intervalo | \((-\infty, \infty)\) | \ (0<a<1\) ">Intervalo | \((-\infty, \infty)\) |
| \ (a">1\) ">\(x\) -interceptar | \((1,0)\) | \ (0<a<1\) ">\(x\) -interceptar | \((1,0)\) |
| \ (a">1\) ">\(y\) -interceptar | Nenhuma | \ (0<a<1\) ">\(y\) -interceptar | Nenhuma |
| \ (a">1\) ">Contém | \((a, 1),\left(\frac{1}{a},-1\right)\) | \ (0<a<1\) ">Contém | \((a, 1),\left(\frac{1}{a},-1\right)\) |
| \ (a">1\) ">Assíntota | \(y\)-eixo | \ (0<a<1\) ">Assíntota | \(y\)-eixo |
| \ (a">1\) ">Forma básica | Aumentando | \ (0<a<1\) ">Forma básica | Decrescente |

Falamos anteriormente sobre como a função logarítmica\(f^{-1}(x)=\log _{a} x\) é o inverso da função exponencial\(f(x)=a^{x}\). Os gráficos na Figura 10.3.12 mostram as funções exponencial (azul) e logarítmica (vermelha) no mesmo gráfico para\(a>1\)\(0<a<1\) e.
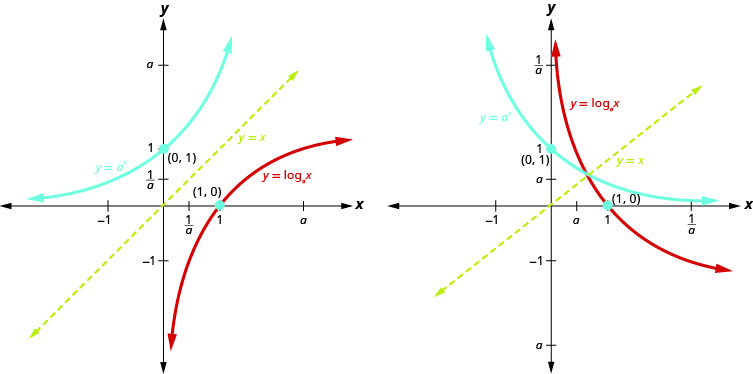
Observe como os gráficos são reflexos um do outro ao longo da linha\(y=x\). Sabemos que isso é verdade para funções inversas. Manter uma visão geral desses gráficos ajudará você a lembrar o domínio e o alcance de cada função. Observe que o\(x\) eixo -é a assíntota horizontal para as funções exponenciais e o\(y\) eixo -é a assíntota vertical para as funções logarítmicas.
Resolver equações logarítmicas
Quando falamos sobre funções exponenciais, introduzimos o número\(e\). Assim como\(e\) era uma base para uma função exponencial, ela também pode ser usada como base para funções logarítmicas. A função logarítmica com base\(e\) é chamada de função logarítmica natural. A função geralmente\(f(x)=\log _{e} x\) é escrita\(f(x)=\ln x\) e a lemos como “el en of”\(x\).
A função\(f(x)=\ln x\) é a função logarítmica natural com base\(e\), onde\(x>0\).
\(y=\ln x\)é equivalente a\(x=e^{y}\)
Quando a base da função logarítmica é\(10\), nós a chamamos de função logarítmica comum e a base não é mostrada. Se a base\(a\) de um logaritmo não for mostrada, assumimos que sim\(10\).
A função\(f(x)=\log x\) é a função logarítmica comum com base\(10\), onde\(x>0\).
\(y=\log x\)é equivalente a\(x=10^{y}\)

Para resolver equações logarítmicas, uma estratégia é mudar a equação para a forma exponencial e, em seguida, resolver a equação exponencial como fizemos antes. À medida que resolvemos equações logarítmicas\(y=log_{a}x\), precisamos lembrar que, para a base\(a\),\(a>0\)\(a≠1\) e. Além disso, o domínio é\(x>0\). Assim como com as equações radicais, devemos verificar nossas soluções para eliminar quaisquer soluções estranhas.
Resolver:
- \(\log _{a} 49=2\)
- \(\ln x=3\)
Solução:
uma.
\(\log _{a} 49=2\)
Reescreva em forma exponencial.
\(a^{2}=49\)
Resolva a equação usando a propriedade raiz quadrada.
\(a=\pm 7\)
A base não pode ser negativa, então eliminamos\(a=-7\).
\(a=7, \quad \cancel{a=-7}\)
Verifique. \(a=7\)
\(\begin{aligned} \log _{a} 49&=2 \\ \log_{7}49&\stackrel{?}{=}2 \\ 7^{2}&\stackrel{?}{=}49 \\ 49&=49 \end{aligned}\)
b.
\(\ln x=3\)
Reescreva em forma exponencial.
\(e^{3}=x\)
Verifique. \(x=e^{3}\)
\(\begin{aligned} \ln x &=3 \\ \ln e^{3} & \stackrel{?}{=} 3 \\ e^{3} &=e^{3} \end{aligned}\)
Resolver:
- \(\log _{a} 121=2\)
- \(\ln x=7\)
- Responda
-
- \(a=11\)
- \(x=e^{7}\)
Resolver:
- \(\log _{a} 64=3\)
- \(\ln x=9\)
- Responda
-
- \(a=4\)
- \(x=e^{9}\)
Resolver:
- \(\log _{2}(3 x-5)=4\)
- \(\ln e^{2 x}=4\)
Solução:
uma.
\(\log _{2}(3 x-5)=4\)
Reescreva em forma exponencial.
\(2^{4}=3 x-5\)
Simplifique.
\(16=3 x-5\)
Resolva a equação.
\(21=3 x\)
\(7=x\)
Verifique. \(x=7\)
\(\begin{aligned} \log _{2}(3 x-5)&=4 \\ \log_{2}(3\cdot7-5)&\stackrel{?}{=}4\\ \log_{2}(16)&\stackrel{?}{=}4 \\ 2^{4}& \stackrel{?}{=}16 \\ 16&=16 \end{aligned}\)
b.
\(\ln e^{2 x}=4\)
Reescreva em forma exponencial.
\(e^{4}=e^{2 x}\)
Como as bases são as mesmas, os expoentes são iguais.
\(4=2 x\)
Resolva a equação.
\(2=x\)
Verifique. \(x=2\)
\(\begin{aligned} \ln e^{2 x} &=4 \\ \ln e^{2 \cdot 2} & \stackrel{?}{=} 4 \\ \ln e^{4} &=4 \\ e^{4} &=e^{4} \end{aligned}\)
Resolver:
- \(\log _{2}(5 x-1)=6\)
- \(\ln e^{3 x}=6\)
- Responda
-
- \(x=13\)
- \(x=2\)
Resolver:
- \(\log _{3}(4 x+3)=3\)
- \(\ln e^{4 x}=4\)
- Responda
-
- \(x=6\)
- \(x=1\)
Use modelos logarítmicos em aplicativos
Há muitas aplicações que são modeladas por equações logarítmicas. Primeiro, examinaremos a equação logarítmica que fornece o nível de decibéis (dB) do som. Os decibéis variam de\(0\), que é quase inaudível\(160\), até, que pode romper um tímpano. O\(10^{−12}\) na fórmula representa a intensidade do som que é quase inaudível.
Nível de som em decibéis
O nível de volume\(D\), medido em decibéis, de um som de intensidade,\(I\), medido em watts por polegada quadrada é
\(D=10 \log \left(\frac{I}{10^{-12}}\right)\)
A exposição prolongada a ruídos que mede\(85\) dB pode causar danos permanentes ao ouvido interno, o que resultará em perda auditiva. Qual é o nível de decibéis da música que vem dos fones de ouvido com intensidade de\(10^{−2}\) watts por polegada quadrada?
Solução:
 |
|
| Substitua no nível de intensidade,\(I\). | 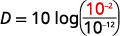 |
| Simplifique. | 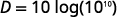 |
| Desde\(\log 10^{10}=10\). |  |
| Multiplique. | 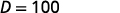 |
| O nível de decibéis da música que vem dos fones de ouvido é\(100\) dB. |
Qual é o nível de decibéis de uma das novas máquinas de lavar louça silenciosas com intensidade de\(10^{−7}\) watts por polegada quadrada?
- Responda
-
As máquinas de lavar louça silenciosas têm um nível de decibéis de\(50\) dB.
Qual é o nível de decibéis do tráfego urbano intenso com intensidade de\(10^{−3}\) watts por polegada quadrada?
- Responda
-
O nível de decibéis do tráfego intenso é\(90\) dB.
A magnitude\(R\) de um terremoto é medida por uma escala logarítmica chamada escala Richter. O modelo é\(R=\log I\), onde\(I\) está a intensidade da onda de choque. Este modelo fornece uma maneira de medir a intensidade do terremoto.
A magnitude\(R\) de um terremoto é medida por\(R=\log I\), onde\(I\) está a intensidade de sua onda de choque.
Em 1906, San Francisco sofreu um intenso terremoto com uma magnitude de\(7.8\) na escala Richter. Mais de\(80\)% da cidade foi destruída pelos incêndios resultantes. Em 2014, Los Angeles sofreu um terremoto moderado medido\(5.1\) na escala Richter e causou danos\(108\) de $ milhões de dólares. Compare as intensidades dos dois terremotos.
Solução:
Para comparar as intensidades, primeiro precisamos converter as magnitudes em intensidades usando a fórmula logarítmica. Em seguida, configuraremos uma proporção para comparar as intensidades.
Converta as magnitudes em intensidades.
\(R=\log I\)
Terremoto de 1906
\(7.8=\log I\)
Converta para a forma exponencial.
\(I=10^{7.8}\)
Terremoto de 2014
\(5.1=\log I\)
Converta para a forma exponencial.
\(I=10^{5.1}\)
Forme uma proporção das intensidades.
\(\frac{\text { Intensity for } 1906}{\text { Intensity for } 2014}\)
Substitua os valores.
\(\frac{10^{7.8}}{10^{5.1}}\)
Divida subtraindo os expoentes.
\(10^{2.7}\)
Avalie.
\(501\)
A intensidade do terremoto de 1906 foi cerca de\(501\) vezes a intensidade do terremoto de 2014.
Em 1906, San Francisco sofreu um intenso terremoto com uma magnitude de\(7.8\) na escala Richter. Em 1989, o terremoto de Loma Prieta também afetou a área de São Francisco e medido\(6.9\) na escala Richter. Compare as intensidades dos dois terremotos.
- Responda
-
A intensidade do terremoto de 1906 foi cerca de\(8\) vezes a intensidade do terremoto de 1989.
Em 2014, o Chile sofreu um intenso terremoto com uma magnitude de\(8.2\) na escala Richter. Em 2014, Los Angeles também sofreu um terremoto medido\(5.1\) na escala Richter. Compare as intensidades dos dois terremotos.
- Responda
-
A intensidade do terremoto no Chile foi cerca de\(1,259\) vezes a intensidade do terremoto em Los Angeles.
Acesse esses recursos on-line para obter instruções e práticas adicionais de avaliação e representação gráfica de funções logarítmicas.
Conceitos-chave
- Propriedades do gráfico de\(y=\log _{a} x\):
| Quando\(a>1\) | Quando\(0<a<1\) | ||
|---|---|---|---|
| \ (a">1\) ">Domínio | \((0, \infty)\) | \ (0<a<1\) ">Domínio | \((0, \infty)\) |
| \ (a">1\) ">Intervalo | \((-\infty, \infty)\) | \ (0<a<1\) ">Intervalo | \((-\infty, \infty)\) |
| \ (a">1\) ">\(x\) -interceptar | \((1,0)\) | \ (0<a<1\) ">\(x\) -interceptar | \((1,0)\) |
| \ (a">1\) ">\(y\) -interceptar | Nenhuma | \ (0<a<1\) ">\(y\) -interceptar | Nenhuma |
| \ (a">1\) ">Contém | \((a, 1),\left(\frac{1}{a},-1\right)\) | \ (0<a<1\) ">Contém | \((a, 1),\left(\frac{1}{a},-1\right)\) |
| \ (a">1\) ">Assíntota | \(y\)-eixo | \ (0<a<1\) ">Assíntota | \(y\)-eixo |
| \ (a">1\) ">Forma básica | Aumentando | \ (0<a<1\) ">Forma básica | Decrescente |

- Nível de som em decibéis: O nível de volume\(D\), medido em decibéis, de um som de intensidade,\(I\), medido em watts por polegada quadrada é\(D=10 \log \left(\frac{I}{10^{-12}}\right)\).
- Intensidade do terremoto: A magnitude\(R\) de um terremoto é medida por\(R=\log I\), onde\(I\) está a intensidade de sua onda de choque.
Glossário
- função logarítmica comum
- A função\(f(x)=\log x\) é a função logarítmica comum com base\(10\), onde\(x>0\).
\(y=\log x\)é equivalente a\(x=10^{y}\)
- função logarítmica
- A função\(f(x)=\log _{a} x\) é a função logarítmica com base\(a\)\(a>0,x>0\), onde,\(a≠1\) e.
\(y=\log _{a} x\)é equivalente a\(x=a^{y}\)
- função logarítmica natural
- A função\(f(x)=\ln x\) é a função logarítmica natural com base\(e\), onde\(x>0\).
\(y=\ln x\)é equivalente a\(x=e^{y}\)


