10.3: Avalie e represente graficamente funções exponenciais
- Page ID
- 183470
Ao final desta seção, você poderá:
- Funções exponenciais gráficas
- Resolva equações exponenciais
- Use modelos exponenciais em aplicativos
Antes de começar, faça este teste de prontidão.
- Simplifique:\(\left(\frac{x^{3}}{x^{2}}\right)\).
Se você perdeu esse problema, consulte o Exemplo 5.13. - Avalie: a.\(2^{0}\)\(\left(\frac{1}{3}\right)^{0}\) b.
Se você perdeu esse problema, consulte o Exemplo 5.14. - Avalie: a.\(2^{−1}\)\(\left(\frac{1}{3}\right)^{-1}\) b.
Se você perdeu esse problema, consulte o Exemplo 5.15.
Grafar funções exponenciais
As funções que estudamos até agora não nos fornecem um modelo para muitos fenômenos que ocorrem naturalmente. Do crescimento das populações e da disseminação de vírus ao decaimento radioativo e ao interesse composto, os modelos são muito diferentes do que estudamos até agora. Esses modelos envolvem funções exponenciais.
Uma função exponencial é uma função da forma\(f(x)=a^{x}\) onde\(a>0\)\(a≠1\) e.
Uma função exponencial, onde\(a>0\) e\(a≠1\), é uma função da forma
\(f(x)=a^{x}\)
Observe que nessa função, a variável é o expoente. Em nossas funções até agora, as variáveis eram a base.

Nossa definição diz\(a≠1\). Se deixarmos\(a=1\), então\(f(x)=a^{x}\) se torna\(f(x)=1^{x}\). Já que\(1^{x}=1\) para todos os números reais,\(f(x)=1\). Essa é a função constante.
Nossa definição também diz\(a>0\). Se deixarmos uma base ser negativa, digamos\(−4\), então não\(f(x)=(−4)^{x}\) é um número real quando\(x=\frac{1}{2}\).
\(\begin{aligned} f(x) &=(-4)^{x} \\ f\left(\frac{1}{2}\right) &=(-4)^{\frac{1}{2}} \\ f\left(\frac{1}{2}\right) &=\sqrt{-4} \text { not a real number } \end{aligned}\)
Na verdade, não\(f(x)=(−4)^{x}\) seria um número real a qualquer momento\(x\) é uma fração com um denominador par. Portanto, nossa definição exige\(a>0\).
Ao representar graficamente algumas funções exponenciais, poderemos ver suas propriedades exclusivas.
No mesmo gráfico do sistema de coordenadas\(f(x)=2^{x}\)\(g(x)=3^{x}\) e.
Solução:
Usaremos a plotagem de pontos para representar graficamente as funções.
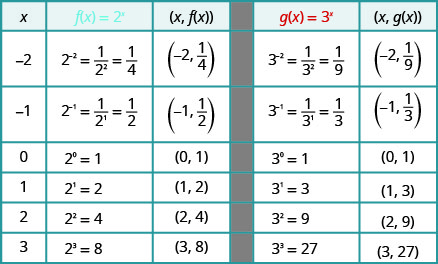
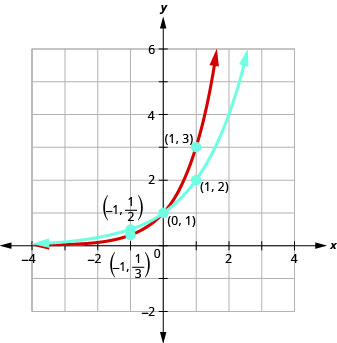
Gráfico:\(f(x)=4^{x}\).
- Resposta
-
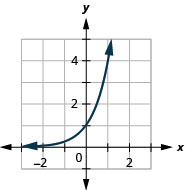
Figura 10.2.4
Gráfico:\(g(x)=5^{x}\)
- Resposta
-
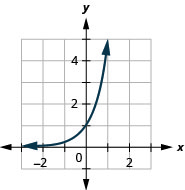
Figura 10.2.5
Se observarmos os gráficos do exemplo 10.2.1 anterior e dos exercícios 10.2.1 e 10.2.2, podemos identificar algumas das propriedades das funções exponenciais.
Os gráficos de\(f(x)=2^{x}\) e\(g(x)=3^{x}\), assim como os gráficos de\(f(x)=4^{x}\) e\(g(x)=5^{x}\), todos têm a mesma forma básica. Essa é a forma que esperamos de uma função exponencial onde\(a>1\).
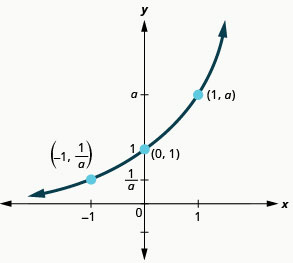
Percebemos que, para cada função, o gráfico contém o ponto\((0,1)\). Isso faz sentido porque,\(a^{0}=1\) para qualquer um\(a\).
O gráfico de cada função\(f(x)=a^{x}\) também contém o ponto\((1,a)\). O gráfico de\(f(x)=2^{x}\) contido\((1,2)\) e o gráfico de\(g(x)=3^{x}\) contido\((1,3)\). Isso faz sentido, pois\(a^{1}=a\).
Observe também que o gráfico de cada função\(f(x)=a^{x}\) também contém o ponto\((−1,\frac{1}{a})\). O gráfico de\(f(x)=2^{x}\) contido\((−1,\frac{1}{2})\) e o gráfico de\(g(x)=3^{x}\) contido\((−1,\frac{1}{3})\). Isso faz sentido, pois\(a^{−1}=\frac{1}{a}\).
Qual é o domínio para cada função? A partir dos gráficos, podemos ver que o domínio é o conjunto de todos os números reais. Não há restrição no domínio. Escrevemos o domínio em notação de intervalo como\((−∞,∞)\).
Veja cada gráfico. Qual é o alcance da função? O gráfico nunca atinge o\(x\) eixo -. O intervalo é composto por todos números positivos. Escrevemos o intervalo em notação de intervalo como\((0,∞)\).
Sempre que um gráfico de uma função se aproxima de uma linha, mas nunca a toca, chamamos essa linha de assíntota. Para as funções exponenciais que estamos observando, o gráfico se aproxima muito do\(x\) eixo -, mas nunca o cruzará, chamamos a linha\(y=0\),\(x\) eixo -, uma assíntota horizontal.
Propriedades do gráfico de\(f(x)=a^{x}\) quando\(a>1\)
| Domínio | \((-\infty, \infty)\) |
| Alcance | \((0, \infty)\) |
| \(x\)-interceptar | Nenhuma |
| \(y\)-interceptar | \((0,1)\) |
| Contém | \((1, a),\left(-1, \frac{1}{a}\right)\) |
| Assíntota | \(x\)-eixo, a linha\(y=0\) |
Nossa definição de uma função exponencial\(f(x)=a^{x}\) diz\(a>0\), mas os exemplos e discussões até agora têm sido sobre funções em que\(a>1\). O que acontece quando\(0<a<1\) o próximo exemplo explorará essa possibilidade.
No mesmo sistema de coordenadas,\(f(x)=\left(\frac{1}{2}\right)^{x}\) grafe\(g(x)=\left(\frac{1}{3}\right)^{x}\) e.
Solução:
Usaremos a plotagem de pontos para representar graficamente as funções.
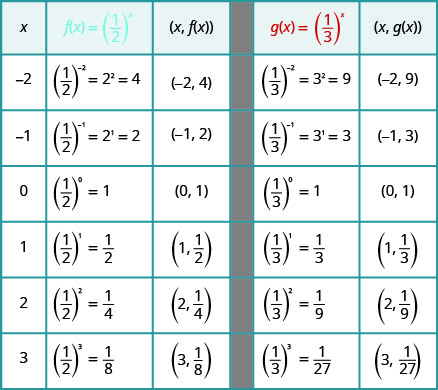
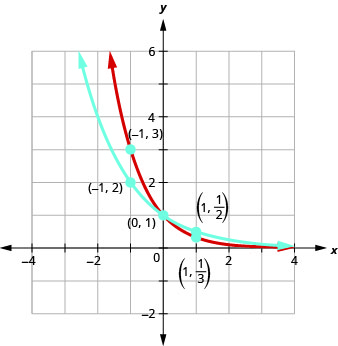
Gráfico:\(f(x)=\left(\frac{1}{4}\right)^{x}\).
- Resposta
-
Figura 10.2.9
Gráfico:\(g(x)=\left(\frac{1}{5}\right)^{x}\).
- Resposta
-
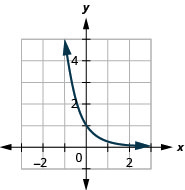
Figura 10.2.10
Agora, vamos dar uma olhada nos gráficos do exemplo 10.2.2 anterior e dos exercícios 10.2.3 e 10.2.4 para que agora possamos identificar algumas das propriedades das funções exponenciais onde\(0<a<1\).
Os gráficos de\(f(x)=\left(\frac{1}{2}\right)^{x}\) e bem\(g(x)=\left(\frac{1}{3}\right)^{x}\) como os gráficos de\(f(x)=\left(\frac{1}{4}\right)^{x}\) e\(g(x)=\left(\frac{1}{5}\right)^{x}\) todos têm a mesma forma básica. Embora essa seja a forma que esperamos de uma função exponencial\(0<a<1\), onde os gráficos descem da esquerda para a direita, enquanto os gráficos anteriores, quando\(a>1\), vão da esquerda para a direita.
Percebemos que, para cada função, o gráfico ainda contém o ponto\((0, 1)\). Isso faz sentido porque,\(a^{0}=1\) para qualquer um\(a\).
Como antes, o gráfico de cada função,\(f(x)=a^{x}\), também contém o ponto\((1,a)\). O gráfico de\(f(x)=\left(\frac{1}{2}\right)^{x}\) contido\(\left(1, \frac{1}{2}\right)\) e o gráfico de\(g(x)=\left(\frac{1}{3}\right)^{x}\) contido\(\left(1, \frac{1}{3}\right)\). Isso faz sentido, pois\(a^{1}=a\).
Observe também que o gráfico de cada função,\(f(x)=a^{x}\), também contém o ponto\(\left(-1, \frac{1}{a}\right)\). O gráfico de\(f(x)=\left(\frac{1}{2}\right)^{x}\) contido\((−1,2)\) e o gráfico de\(g(x)=\left(\frac{1}{3}\right)^{x}\) contido\((−1,3)\). Isso faz sentido, pois\(a^{-1}=\frac{1}{a}\).
Qual é o domínio e o intervalo de cada função? A partir dos gráficos, podemos ver que o domínio é o conjunto de todos os números reais e escrevemos o domínio em notação de intervalo como\((−∞,∞)\). Novamente, o gráfico nunca atinge o\(x\) eixo -. O intervalo é composto por todos números positivos. Escrevemos o intervalo em notação de intervalo como\((0,∞)\).
Resumiremos essas propriedades no gráfico abaixo. O que também inclui quando\(a>1\).
Propriedades do gráfico de\(f(x)=a^{x}\)
| Quando\(a>1\) | Quando\(0<a<1\) | ||
|---|---|---|---|
| \ (a">1\) ">Domínio | \((-\infty, \infty)\) | \ (0<a<1\) ">Domínio | \((-\infty, \infty)\) |
| \ (a">1\) ">Intervalo | \((0, \infty)\) | \ (0<a<1\) ">Intervalo | \((0, \infty)\) |
| \ (a">1\) ">\(x\) -interceptar | nenhum | \ (0<a<1\) ">\(x\) -interceptar | nenhum |
| \ (a">1\) ">\(y\) -interceptar | \((0,1)\) | \ (0<a<1\) ">\(y\) -interceptar | \((0,1)\) |
| \ (a">1\) ">Contém | \((1, a),\left(-1, \frac{1}{a}\right)\) | \ (0<a<1\) ">Contém | \((1, a),\left(-1, \frac{1}{a}\right)\) |
| \ (a">1\) ">Assíntota |
\(x\)-eixo, a linha\(y=0\) |
\ (0<a<1\) ">Assíntota | \(x\)-eixo, a linha\(y=0\) |
| \ (a">1\) ">Forma básica | aumentando | \ (0<a<1\) ">Forma básica | diminuindo |
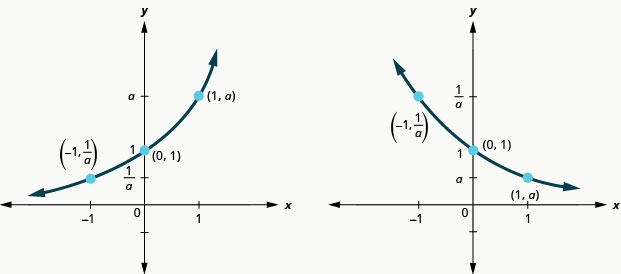
É importante observarmos que esses dois gráficos são individuais, pois ambos passam no teste da linha horizontal. Isso significa que a função exponencial terá um inverso. Vamos analisar isso mais tarde.
Quando graficamos funções quadráticas, conseguimos representar graficamente usando tradução em vez de apenas traçar pontos. Isso funcionará na representação gráfica de funções exponenciais?
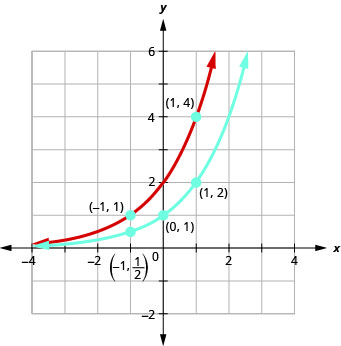
No mesmo gráfico do sistema de coordenadas\(f(x)=2^{x}\)\(g(x)=2^{x+1}\) e.
Solução:
Usaremos a plotagem de pontos para representar graficamente as funções.

No mesmo sistema de coordenadas, grafe:\(f(x)=2^{x}\)\(g(x)=2^{x-1}\) e.
- Resposta
-
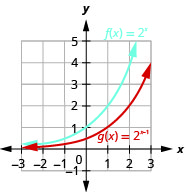
Figura 10.2.14
No mesmo sistema de coordenadas,\(f(x)=3^{x}\) grafe\(g(x)=3^{x+1}\) e.
- Resposta
-
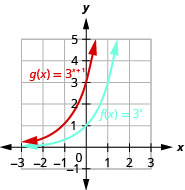
Figura 10.2.15
Observando os gráficos das funções\(f(x)=2^{x}\) e\(g(x)=2^{x+1}\) no último exemplo, vemos que adicionar uma no expoente causou um deslocamento horizontal de uma unidade para a esquerda. Reconhecer esse padrão nos permite representar graficamente outras funções com o mesmo padrão por tradução.
Vamos agora considerar outra situação que pode ser representada graficamente mais facilmente por tradução, uma vez que reconhecemos o padrão.
No mesmo gráfico do sistema de coordenadas\(f(x)=3^{x}\)\(g(x)=3^{x}-2\) e.
Solução:
Usaremos a plotagem de pontos para representar graficamente as funções.
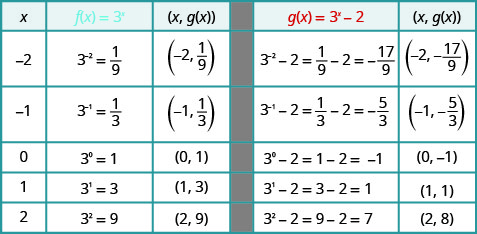
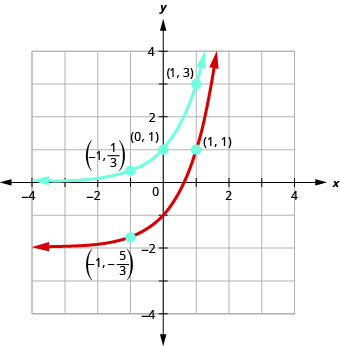
No mesmo sistema de coordenadas,\(f(x)=3^{x}\) grafe\(g(x)=3^{x}+2\) e.
- Resposta
-
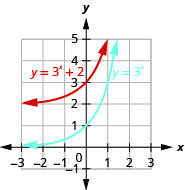
Figura 10.2.18
No mesmo sistema de coordenadas,\(f(x)=4^{x}\) grafe\(g(x)=4^{x}-2\) e.
- Resposta
-
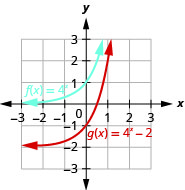
Figura 10.2.19
Observando os gráficos das funções\(f(x)=3^{x}\) e\(g(x)=3^{x}−2\) no último exemplo, vemos que a subtração\(2\) causou uma mudança vertical de duas unidades para baixo. Observe que a assíntota horizontal também deslocou\(2\) unidades para baixo. Reconhecer esse padrão nos permite representar graficamente outras funções com o mesmo padrão por tradução.
Todas as nossas funções exponenciais tiveram um número inteiro ou um número racional como base. Agora veremos uma função exponencial com um número irracional como base.
Antes de podermos examinar essa função exponencial, precisamos definir o número irracional,\(e\). Esse número é usado como base em muitas aplicações nas ciências e nos negócios que são modeladas por funções exponenciais. O número é definido como o valor de\(\left(1+\frac{1}{n}\right)^{n}\) à medida\(n\) que fica cada vez maior. Dizemos que, à medida que\(n\) se aproxima do infinito, ou aumenta sem limites. A tabela mostra o valor de\(\left(1+\frac{1}{n}\right)^{n}\) para vários valores de\(n\).
| \(n\) | \(\left(1+\frac{1}{n}\right)^{n}\) |
|---|---|
| \ (n\) ">\(1\) | \ (\ left (1+\ frac {1} {n}\ direita) ^ {n}\) ">\(2\) |
| \ (n\) ">\(2\) | \ (\ left (1+\ frac {1} {n}\ direita) ^ {n}\) ">\(2.25\) |
| \ (n\) ">\(5\) | \ (\ left (1+\ frac {1} {n}\ direita) ^ {n}\) ">\(2.48832\) |
| \ (n\) ">\(10\) | \ (\ left (1+\ frac {1} {n}\ direita) ^ {n}\) ">\(2.59374246\) |
| \ (n\) ">\(100\) | \ (\ left (1+\ frac {1} {n}\ direita) ^ {n}\) ">\(2.704813829 \ldots\) |
| \ (n\) ">\(1,000\) | \ (\ left (1+\ frac {1} {n}\ direita) ^ {n}\) ">\(2.716923932 \ldots\) |
| \ (n\) ">\(10,000\) | \ (\ left (1+\ frac {1} {n}\ direita) ^ {n}\) ">\(2.718145927 \ldots\) |
| \ (n\) ">\(100,000\) | \ (\ left (1+\ frac {1} {n}\ direita) ^ {n}\) ">\(2.718268237 \ldots\) |
| \ (n\) ">\(1,000,000\) | \ (\ left (1+\ frac {1} {n}\ direita) ^ {n}\) ">\(2.718280469 \ldots\) |
| \ (n\) ">\(1,000,000,000\) | \ (\ left (1+\ frac {1} {n}\ direita) ^ {n}\) ">\(2.718281827 \ldots\) |
\(e \approx 2.718281827\)
O número\(e\) é como o número\(π\) em que usamos um símbolo para representá-lo porque sua representação decimal nunca para ou se repete. O número irracional\(e\) é chamado de base natural.
Base natural\(e\)
O número\(e\) é definido como o valor de\(\left(1+\frac{1}{n}\right)^{n}\), à medida que\(n\) aumenta sem limite. Dizemos que, quando\(n\) se aproxima do infinito,
\(e \approx 2.718281827\)
A função exponencial, cuja base é\(e\),\(f(x)=e^{x}\) é chamada de função exponencial natural.
Função exponencial natural
A função exponencial natural é uma função exponencial cuja base é\(e\)
\(f(x)=e^{x}\)
O domínio é\((−∞,∞)\) e o intervalo é\((0,∞)\).
Vamos representar graficamente a função\(f(x)=e^{x}\) no mesmo sistema de coordenadas que\(g(x)=2^{x}\)\(h(x)=3^{x}\) e.
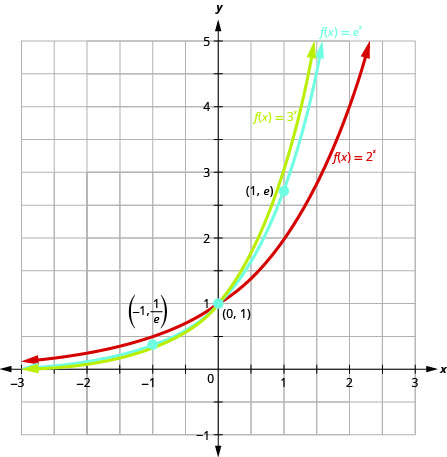
Observe que o gráfico de\(f(x)=e^{x}\) está “entre” os gráficos de\(g(x)=2^{x}\)\(h(x)=3^{x}\) e. Isso faz sentido como\(2<e<3\)?
Resolva equações exponenciais
As equações que incluem uma expressão exponencial\(a^{x}\) são chamadas de equações exponenciais. Para resolvê-los, usamos uma propriedade que diz tanto quanto\(a>0\) e\(a≠1\), se\(a^{x}=a^{y}\) então, é verdade que\(x=y\). Em outras palavras, em uma equação exponencial, se as bases forem iguais, os expoentes serão iguais.
Propriedade individual das equações exponenciais
Para\(a>0\) e\(a≠1\),
Se\(a^{x}=a^{y}\), então\(x=y\).
Para usar essa propriedade, devemos ter certeza de que os dois lados da equação são escritos com a mesma base.
Resolver:\(3^{2 x-5}=27\).
Solução:
| Etapa 1: Escreva os dois lados da equação com a mesma base. | Como o lado esquerdo tem base\(3\), escrevemos o lado direito com base\(3\). \(27=3^{3}\) | \(3^{2 x-5}=27\) \(3^{2 x-5}=3^{3}\) |
| Etapa 2: Escreva uma nova equação definindo os expoentes iguais. | Como as bases são as mesmas, os expoentes devem ser iguais. | \(2x-5=3\) |
| Etapa 3: Resolva a equação. |
Adicione\(5\) a cada lado. Divida por\(2\). |
\(\begin{aligned} 2 x &=8 \\ x &=4 \end{aligned}\) |
| Etapa 4: verifique a solução. | Substitua\(x=4\) na equação original. | \(\begin{aligned} 3^{2 x-5} &=27 \\ 3^{2 \cdot \color{red}{4}\color{black}{-}5} & \stackrel{?}{=} 27 \\ 3^{3} &\stackrel{?}{=}27 \\ 27 &=27 \end{aligned}\) |
Resolver:\(3^{3 x-2}=81\).
- Resposta
-
\(x=2\)
Resolver:\(7^{x-3}=7\).
- Resposta
-
\(x=4\)
As etapas estão resumidas abaixo.
Como resolver uma função exponencial
- Escreva os dois lados da equação com a mesma base, se possível.
- Escreva uma nova equação definindo os expoentes iguais.
- Resolva a equação.
- Verifique a solução.
No próximo exemplo, usaremos nossas propriedades em expoentes.
Resolver\(\frac{e^{x^{2}}}{e^{3}}=e^{2 x}\).
Solução:
| \(\frac{e^{x^{2}}}{e^{3}}=e^{2 x}\) | |
| Use a propriedade dos expoentes:\(\frac{a^{m}}{a^{n}}=a^{m-n}\). | \(e^{x^{2}-3}=e^{2 x}\) |
| Escreva uma nova equação definindo os expoentes iguais. | \(x^{2}-3=2 x\) |
| Resolva a equação. | \(x^{2}-2 x-3=0\) |
| \((x-3)(x+1)=0\) | |
| \(x=3, x=-1\) | |
| Verifique as soluções. | |
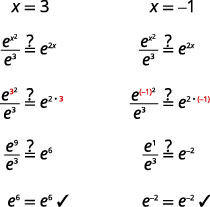 |
Resolver:\(\frac{e^{x^{2}}}{e^{x}}=e^{2}\).
- Resposta
-
\(x=-1, x=2\)
Resolver:\(\frac{e^{x^{2}}}{e^{x}}=e^{6}\).
- Resposta
-
\(x=-2, x=3\)
Use modelos exponenciais em aplicativos
As funções exponenciais modelam muitas situações. Se você possui uma conta bancária, já experimentou o uso de uma função exponencial. Existem duas fórmulas usadas para determinar o saldo na conta quando os juros são ganhos. Se um principal,\(P\), for investido a uma taxa de juros\(r\),, por\(t\) anos, o novo saldo\(A\),, dependerá da frequência com que os juros são compostos. Se os juros forem compostos\(n\) vezes por ano, usamos a fórmula\(A=P\left(1+\frac{r}{n}\right)^{n t}\). Se os juros forem compostos continuamente, usamos a fórmula\(A=Pe^{rt}\). Essas são as fórmulas para juros compostos.
Juros compostos
Para um principal,\(P\), investido a uma taxa de juros\(r\), há\(t\) anos, o novo saldo,\(A\), é:
\(\begin{array}{ll}{A=P\left(1+\frac{r}{n}\right)^{n t}} & {\text { when compounded } n \text { times a year. }} \\ {A=P e^{r t}} & {\text { when compounded continuously. }}\end{array}\)
Ao trabalhar com as fórmulas Interest, geralmente é útil identificar primeiro os valores das variáveis e depois substituí-las pela fórmula.
Um total de $\(10,000\) foi investido em um fundo universitário para um novo neto. Se a taxa de juros for\(5\)%, quanto estará na conta em\(18\) anos por cada método de composição?
- composto trimestral
- composto mensal
- composto continuamente
Solução:
Identifique os valores de cada variável nas fórmulas. Lembre-se de expressar a porcentagem como decimal.
\(\begin{aligned} A &=? \\ P &=\$ 10,000 \\ r &=0.05 \\ t &=18 \text { years } \end{aligned}\)
a. Para composição trimestral,\(n=4\). Há\(4\) trimestres em um ano.
\(A=P\left(1+\frac{r}{n}\right)^{n t}\)
Substitua os valores na fórmula.
\(A=10,000\left(1+\frac{0.05}{4}\right)^{4 \cdot 18}\)
Calcule o valor. Tenha cuidado ao considerar a ordem das operações ao inserir a expressão em sua calculadora.
\(A=\$ 24,459.20\)
b. Para composição mensal,\(n=12\) .Há\(12\) meses em um ano.
\(A=P\left(1+\frac{r}{n}\right)^{n t}\)
Substitua os valores na fórmula.
\(A=10,000\left(1+\frac{0.05}{12}\right)^{12 \cdot 18}\)
Calcule o valor.
\(A=\$ 24,550.08\)
c. Para composição contínua,
\(A=P e^{r t}\)
Substitua os valores na fórmula.
\(A=10,000 e^{0.05 \cdot 18}\)
Calcule o valor.
\(A=\$ 24,596.03\)
Angela investiu $\(15,000\) em uma conta poupança. Se a taxa de juros for\(4\)%, quanto estará na conta em\(10\) anos por cada método de composição?
- composto trimestral
- composto mensal
- composto continuamente
- Resposta
-
- $\(22,332.96\)
- $\(22,362.49\)
- $\(22,377.37\)
Allan investiu $\(10,000\) em um fundo mútuo. Se a taxa de juros for\(5\)%, quanto estará na conta em\(15\) anos por cada método de composição?
- composto trimestral
- composto mensal
- composto continuamente
- Resposta
-
- $\(21,071.81\)
- $\(21,137.04\)
- $\(21,170.00\)
Outros tópicos que são modelados por funções exponenciais envolvem crescimento e decadência. Ambos também usam a fórmula\(A=Pe^{rt}\) que usamos para o crescimento do dinheiro. Para crescimento e decadência, geralmente usamos\(A_{0}\), como quantidade original, em vez de chamá-la\(P\), o principal. Vemos que o crescimento exponencial tem uma taxa de crescimento positiva e a queda exponencial tem uma taxa de crescimento negativa.
Crescimento e decadência exponenciais
Para uma quantidade original,\(A_{0}\), que cresce ou decai a uma taxa,\(r\), por um certo tempo,\(t\), a quantidade final,\(A\), é:
\(A=A_{0} e^{r t}\)
O crescimento exponencial é normalmente observado no crescimento de populações de humanos, animais ou bactérias. Nosso próximo exemplo analisa o crescimento de um vírus.
Chris é pesquisador do Centro de Controle e Prevenção de Doenças e está tentando entender o comportamento de um vírus novo e perigoso. Ele inicia seu experimento com\(100\) o vírus que cresce a uma taxa de\(25\)% por hora. Ele verificará o vírus em\(24\) horas. Quantos vírus ele encontrará?
Solução:
Identifique os valores de cada variável nas fórmulas. Certifique-se de colocar a porcentagem na forma decimal. Certifique-se de que as unidades correspondam — a taxa é por hora e o tempo está em horas.
\(\begin{aligned} A &=? \\ A_{0} &=100 \\ r &=0.25 / \text { hour } \\ t &=24 \text { hours } \end{aligned}\)
Substitua os valores na fórmula:\(A=A_{0} e^{r t}\).
\(A=100 e^{0.25 \cdot 24}\)
Calcule o valor.
\(A=40,342.88\)
Arredonde até o vírus inteiro mais próximo.
\(A=40,343\)
O pesquisador encontrará\(40,343\) vírus.
Outra pesquisadora do Centro de Controle e Prevenção de Doenças, Lisa, está estudando o crescimento de uma bactéria. Ela inicia seu experimento com\(50\) a bactéria que cresce a uma taxa de\(15\)% por hora. Ele verificará as bactérias a cada\(8\) hora. Quantas bactérias ele encontrará em\(8\) horas?
- Resposta
-
Ela encontrará\(166\) bactérias.
Maria, bióloga, está observando o padrão de crescimento de um vírus. Ela começa com\(100\) o vírus que cresce a uma taxa de\(10\)% por hora. Ela verificará o vírus em\(24\) horas. Quantos vírus ela encontrará?
- Resposta
-
Ela encontrará\(1,102\) vírus.
Acesse esses recursos on-line para obter instruções e práticas adicionais de avaliação e representação gráfica de funções exponenciais.
Conceitos-chave
- Propriedades do gráfico de\(f(x)=a^{x}\):
| Quando\(a>1\) | Quando\(0<a<1\) | ||
|---|---|---|---|
| \ (a">1\) ">Domínio | \((-\infty, \infty)\) | \ (0<a<1\) ">Domínio | \((-\infty, \infty)\) |
| \ (a">1\) ">Intervalo | \((0, \infty)\) | \ (0<a<1\) ">Intervalo | \((0, \infty)\) |
| \ (a">1\) ">\(x\) -interceptar | nenhum | \ (0<a<1\) ">\(x\) -interceptar | nenhum |
| \ (a">1\) ">\(y\) -interceptar | \((0,1)\) | \ (0<a<1\) ">\(y\) -interceptar | \((0,1)\) |
| \ (a">1\) ">Contém | \((1, a),\left(-1, \frac{1}{a}\right)\) | \ (0<a<1\) ">Contém | \((1, a),\left(-1, \frac{1}{a}\right)\) |
| \ (a">1\) ">Assíntota |
\(x\)-eixo, a linha\(y=0\) |
\ (0<a<1\) ">Assíntota | \(x\)-eixo, a linha\(y=0\) |
| \ (a">1\) ">Forma básica | aumentando | \ (0<a<1\) ">Forma básica | diminuindo |
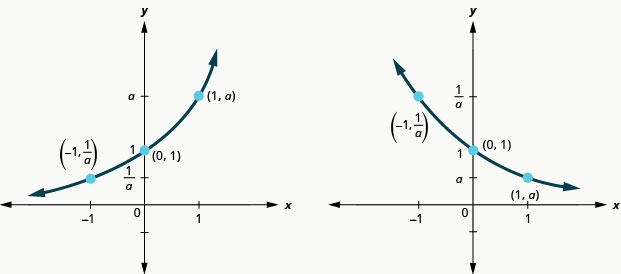
- Propriedade individual das equações exponenciais:
Para\(a>0\) e\(a≠1\),\(A=A_{0} e^{r t}\)
- Como resolver uma equação exponencial
- Escreva os dois lados da equação com a mesma base, se possível.
- Escreva uma nova equação definindo os expoentes iguais.
- Resolva a equação.
- Verifique a solução.
- Juros compostos: Para um principal\(P\), investido a uma taxa de juros\(r\),, por\(t\) anos, o novo saldo,\(A\), é
\(\begin{array}{ll}{A=P\left(1+\frac{r}{n}\right)^{n t}} & {\text { when compounded } n \text { times a year. }} \\ {A=P e^{r t}} & {\text { when compounded continuously. }}\end{array}\) - Crescimento e decaimento exponenciais: Para uma quantidade original,\(A_{0}\) que cresce ou decai a uma taxa,\(r\), por um certo tempo\(t\), a quantidade final,\(A\), é\(A=A_{0}e^{rt}\).
Glossário
- assíntota
- Uma linha na qual um gráfico de uma função se aproxima, mas nunca toca.
- função exponencial
- Uma função exponencial, onde\(a>0\) e\(a≠1\), é uma função da forma\(f(x)=a^{x}\).
- base natural
- O número\(e\) é definido como o valor de\((1+\frac{1}{n})^{n}\), à medida\(n\) que fica cada vez maior. Dizemos que, à medida que\(n\) aumenta sem limites,\(e≈2.718281827...\)
- função exponencial natural
- A função exponencial natural é uma função exponencial cuja base é\(e\):\(f(x)=e^{x}\). O domínio é\((−∞,∞)\) e o intervalo é\((0,∞)\).


