10.2: Encontrando funções compostas e inversas
- Page ID
- 183437
Ao final desta seção, você poderá:
- Encontre e avalie funções compostas
- Determine se uma função é individual
- Encontre o inverso de uma função
Antes de começar, faça este teste de prontidão.
- Se\(f(x)=2 x-3\) e\(g(x)=x^{2}+2 x-3\), encontre\(f(4)\).
Se você perdeu esse problema, revise o Exemplo 3.48. - Resolva para\(x\),\(3x+2y=12\).
Se você perdeu esse problema, consulte o Exemplo 2.31. - Simplifique:\(5 \frac{(x+4)}{5}-4\).
Se você perdeu esse problema, revise o Exemplo 1.25.
Neste capítulo, apresentaremos dois novos tipos de funções, funções exponenciais e funções logarítmicas. Essas funções são amplamente usadas nos negócios e nas ciências, como veremos.
Encontre e avalie funções compostas
Antes de introduzirmos as funções, precisamos examinar outra operação sobre funções chamada composição. Na composição, a saída de uma função é a entrada de uma segunda função. Para funções\(f\) e\(g\), a composição é escrita\(f∘g\) e definida por\((f∘g)(x)=f(g(x))\).
Lemos\(f(g(x))\) como “\(f\)\(g\)de”\(x\).
Para fazer uma composição, a saída da primeira função,\(g(x)\), se torna a entrada da segunda função e\(f\), portanto, devemos ter certeza de que ela faz parte do domínio de\(f\).
A composição das funções\(f\) e\(g\) é escrita\(f \cdot g\) e é definida por
\((f \circ g)(x)=f(g(x))\)
Lemos\(f(g(x))\) a partir\(f\)\(g\) de\(x\).
Na verdade, usamos a composição sem usar a notação muitas vezes antes. Quando representamos graficamente funções quadráticas usando traduções, estávamos compondo funções. Por exemplo, se primeiro graficássemos\(g(x)=x^{2}\) como uma parábola e depois a deslocarmos verticalmente quatro unidades, estávamos usando a composição definida por\((f∘g)(x)=f(g(x))\) where\(f(x)=x−4\).
Para funções\(f(x)=4x-5\) e\(g(x)=2x+3\), encontre
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
Solução:
-
Use a definição de\((f \circ g)(x)\). 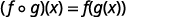

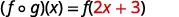

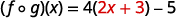
Distribuir. 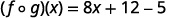
Simplifique. 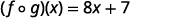
Tabela 10.1.1 -
Use a definição de\((f \circ g)(x)\). 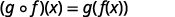

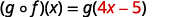

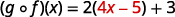
Distribuir. 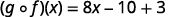
Simplifique. 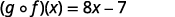
Tabela 10.1.2
Observe a diferença no resultado na parte a. e na parte b.
c. Observe que isso\((f \cdot g)(x)\) é diferente de\((f \circ g)(x)\). Na parte a. fizemos a composição das funções. Agora, na parte c. não os estamos compondo, estamos multiplicando-os.
Use a definição de\((f \cdot g)(x)\).
\((f \cdot g)(x)=f(x) \cdot g(x)\)
\(f(x)=4 x-5\)Substitua\(g(x)=2 x+3\) e.
\((f \cdot g)(x)=(4 x-5) \cdot(2 x+3)\)
Multiplique.
\((f \cdot g)(x)=8 x^{2}+2 x-15\)
Para funções\(f(x)=3x-2\) e\(g(x)=5x+1\), encontre
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
- Responda
-
- \(15x+1\)
- \(15x-9\)
- \(15 x^{2}-7 x-2\)
Para funções e\(f(x)=4 x-3\)\(g(x)=6x-5\), encontre
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
- Responda
-
- \(24 x-23\)
- \(24 x-23\)
- \(24 x^{2}-38 x+15\)
No próximo exemplo, avaliaremos uma composição para um valor específico.
Para funções\(f(x)=x^{2}-4\)\(g(x)=3 x+2\), e encontre:
- \((f \circ g)(-3)\)
- \((g \circ f)(-1)\)
- \((f \circ f)(2)\)
Solução:
-
Use a definição de\((f \circ g)(-3)\). 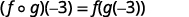

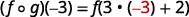
Simplifique. 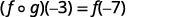

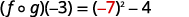
Simplifique. 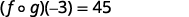
Tabela 10.1.3 -
Use a definição de\((g \circ f)(-1)\). 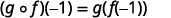

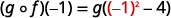
Simplifique. 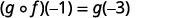

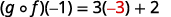
Simplifique. 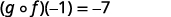
Tabela 10.1.4 -
Use a definição de\((f \circ f)(2)\). 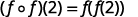

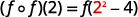
Simplifique. 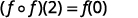

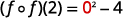
Simplifique. 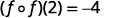
Tabela 10.1.5
Para funções e\(f(x)=x^{2}-9\)\(g(x)=2x+5\), encontre
- \((f \circ g)(-2)\)
- \((g \circ f)(-3)\)
- \((f \circ f)(4)\)
- Responda
-
- \(-8\)
- \(5\)
- \(40\)
Para funções e\(f(x)=x^{2}+1\)\(g(x)=3x-5\), encontre
- \((f \circ g)(-1)\)
- \((g \circ f)(2)\)
- \((f \circ f)(-1)\)
- Responda
-
- \(65\)
- \(10\)
- \(5\)
Determine se uma função é individual
Quando introduzimos funções pela primeira vez, dissemos que uma função é uma relação que atribui a cada elemento em seu domínio exatamente um elemento no intervalo. Para cada par ordenado na relação, cada\(x\) valor -é combinado com apenas um\(y\) valor -.
Usamos o exemplo de aniversário para nos ajudar a entender a definição. Toda pessoa faz aniversário, mas ninguém tem dois aniversários e não há problema em duas pessoas compartilharem um aniversário. Como cada pessoa tem exatamente um aniversário, essa relação é uma função.

Uma função é individual se cada valor no intervalo tiver exatamente um elemento no domínio. Para cada par ordenado na função, cada valor y é combinado com apenas um\(x\) valor.
Nosso exemplo da relação de aniversário não é uma função individual. Duas pessoas podem compartilhar o mesmo aniversário. O valor do intervalo em 2 de agosto é o aniversário de Liz e June e, portanto, um valor de intervalo tem dois valores de domínio. Portanto, a função não é individual.
Uma função é individual se cada valor no intervalo corresponder a um elemento no domínio. Para cada par ordenado na função, cada\(y\) valor -é combinado com apenas um\(x\) valor. Não há\(y\) valores repetidos.
Para cada conjunto de pares ordenados, determine se ela representa uma função e, em caso afirmativo, se a função é individual.
- \(\{(-3,27),(-2,8),(-1,1),(0,0),(1,1),(2,8),(3,27)\}\)
- \(\{(0,0),(1,1),(4,2),(9,3),(16,4)\}\)
Solução:
- \(\{(-3,27),(-2,8),(-1,1),(0,0),(1,1),(2,8),(3,27)\}\)
Cada\(x\) valor -é combinado com apenas um\(y\) valor. Então, essa relação é uma função.
Mas cada\(y\) valor -não está emparelhado com apenas um\(x\) valor -,\((−3,27)\) e\((3,27)\), por exemplo. Portanto, essa função não é individual.
- \(\{(0,0),(1,1),(4,2),(9,3),(16,4)\}\)
Cada\(x\) valor -é combinado com apenas um\(y\) valor. Então, essa relação é uma função.
Como cada\(y\) valor -é pareado com apenas um\(x\) valor -, essa função é individual.
Para cada conjunto de pares ordenados, determine se ela representa uma função e, em caso afirmativo, é a função um a um.
- \(\{(-3,-6),(-2,-4),(-1,-2),(0,0),(1,2),(2,4),(3,6)\}\)
- \(\{(-4,8),(-2,4),(-1,2),(0,0),(1,2),(2,4),(4,8)\}\)
- Responda
-
- Função um para um
- Função; não um para um
Para cada conjunto de pares ordenados, determine se ela representa uma função e, em caso afirmativo, é a função um a um.
- \(\{(27,-3),(8,-2),(1,-1),(0,0),(1,1),(8,2),(27,3)\}\)
- \(\{(7,-3),(-5,-4),(8,0),(0,0),(-6,4),(-2,2),(-1,3)\}\)
- Responda
-
- Não é uma função
- Função; não um para um
Para nos ajudar a determinar se uma relação é uma função, usamos o teste de linha vertical. Um conjunto de pontos em um sistema de coordenadas retangulares é o gráfico de uma função se cada linha vertical cruzar o gráfico em no máximo um ponto. Além disso, se alguma linha vertical cruzar o gráfico em mais de um ponto, o gráfico não representa uma função.
A linha vertical está representando um\(x\) valor -e verificamos se ela cruza o gráfico em apenas um\(y\) valor. Então é uma função.
Para verificar se uma função é individual, usamos um processo semelhante. Usamos uma linha horizontal e verificamos se cada linha horizontal cruza o gráfico em apenas um ponto. A linha horizontal representa um\(y\) valor -e verificamos se ela cruza o gráfico em apenas um\(x\) valor. Se cada linha horizontal intersecta o gráfico de uma função em no máximo um ponto, é uma função individual. Este é o teste da linha horizontal.
Teste de linha horizontal
Se cada linha horizontal intersecta o gráfico de uma função em no máximo um ponto, é uma função individual.
Podemos testar se um gráfico de uma relação é uma função usando o teste de linha vertical. Podemos então saber se a função é individual aplicando o teste de linha horizontal.
Determinar
- se cada gráfico é o gráfico de uma função e, em caso afirmativo,
- se é um para um
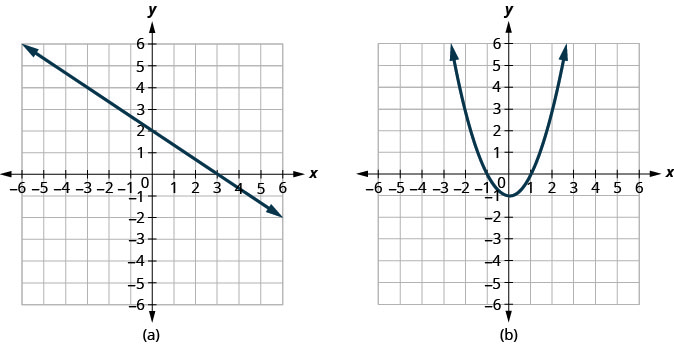
Solução:
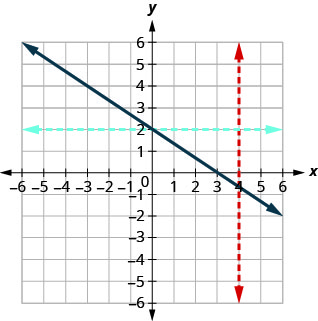
Figura 10.1.40
Como qualquer linha vertical cruza o gráfico em no máximo um ponto, o gráfico é o gráfico de uma função. Como qualquer linha horizontal cruza o gráfico em no máximo um ponto, o gráfico é o gráfico de uma função individual.
b.
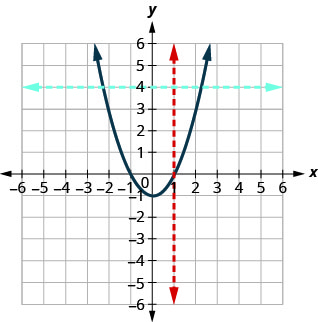
Como qualquer linha vertical cruza o gráfico em no máximo um ponto, o gráfico é o gráfico de uma função. A linha horizontal mostrada no gráfico a cruza em dois pontos. Esse gráfico não representa uma função individual.
Determinar
- se cada gráfico é o gráfico de uma função e, em caso afirmativo,
- se é um para um
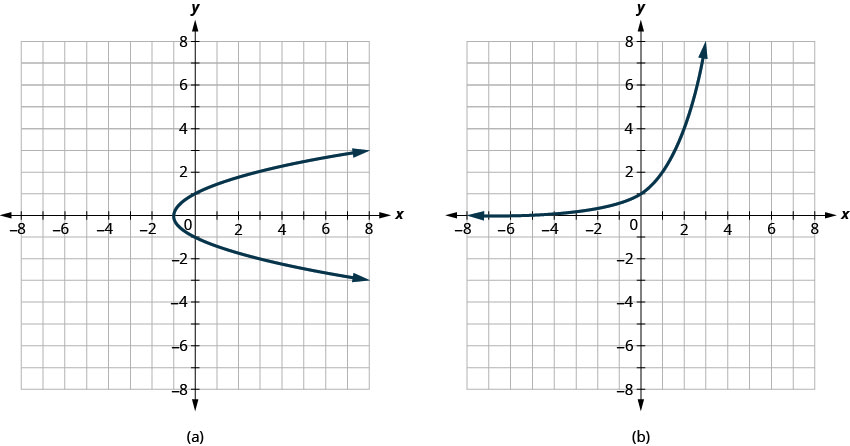
- Responda
-
- Não é uma função
- Função um para um
Determinar
- se cada gráfico é o gráfico de uma função e, em caso afirmativo,
- se é um para um
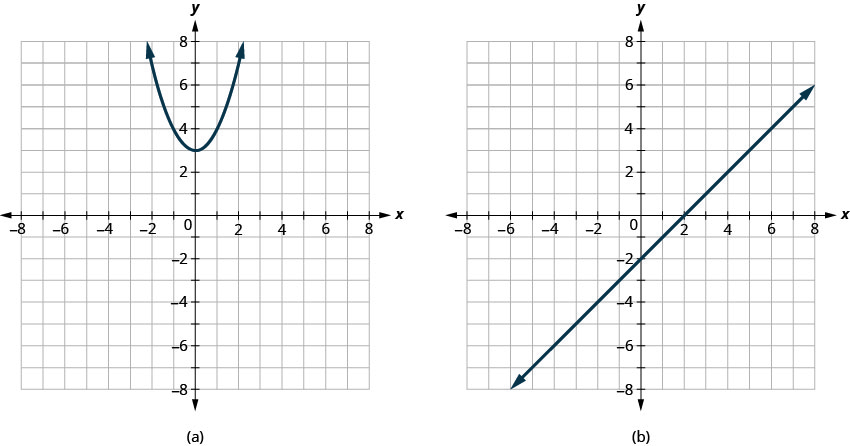
- Responda
-
- Função; não um para um
- Função um para um
Encontre o inverso de uma função
Vejamos uma função individual\(f\), representada pelos pares ordenados\(\{(0,5),(1,6),(2,7),(3,8)\}\). Para cada\(x\) -value,\(f\) adiciona\(5\) para obter o\(y\) valor -. Para 'desfazer' a adição de\(5\), subtraímos\(5\) de cada\(y\) valor -e voltamos ao\(x\) valor original. Podemos chamar isso de “tomar o inverso de\(f\)” e nomear a função\(f^{−1}\).
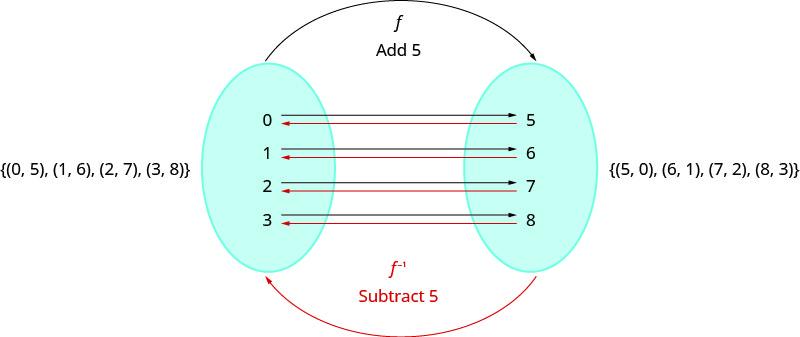
Observe que os pares ordenados de\(f\) e\(f^{−1}\) têm seus\(x\) valores -e\(y\) -valores invertidos. O domínio de\(f\) é o intervalo de\(f^{−1}\) e o domínio de\(f^{−1}\) é o intervalo de\(f\).
Inverso de uma função definida por pares ordenados
Se\(f(x)\) for uma função um-para-um cujos pares ordenados são da forma\((x,y)\), então sua função inversa\(f^{−1}(x)\) é o conjunto de pares ordenados\((y,x)\).
No próximo exemplo, encontraremos o inverso de uma função definida por pares ordenados.
Encontre o inverso da função\(\{(0,3),(1,5),(2,7),(3,9)\}\). Determine o domínio e o alcance da função inversa.
Solução:
Essa função é individual, pois cada\(x\) valor -é pareado com exatamente um\(y\) valor.
Para encontrar o inverso, invertemos\(x\) os valores\(y\) -e os valores -nos pares ordenados da função.
\(\begin{array}{ll} {\text{Function}}&{\{(0,3),(1,5),(2,7),(3,9)\}} \\ {\text{Inverse Function}}& {\{(3,0), (5,1), (7,2), (9,3)\}} \\ {\text{Domain of Inverse Function}}&{\{3, 5, 7, 9\}} \\ {\text{Range of Inverse Function}}&{\{0, 1, 2, 3\}} \end{array}\)
Encontre o inverso de\(\{(0,4),(1,7),(2,10),(3,13)\}\). Determine o domínio e o alcance da função inversa.
- Responda
-
Função inversa:\(\{(4,0),(7,1),(10,2),(13,3)\}\). Domínio:\(\{4,7,10,13\}\). Alcance:\(\{0,1,2,3\}\).
Encontre o inverso de\(\{(-1,4),(-2,1),(-3,0),(-4,2)\}\). Determine o domínio e o alcance da função inversa.
- Responda
-
Função inversa:\(\{(4,-1),(1,-2),(0,-3),(2,-4)\}\). Domínio:\(\{0,1,2,4\}\). Alcance:\(\{-4,-3,-2,-1\}\).
Acabamos de observar que se\(f(x)\) é uma função um-para-um cujos pares ordenados são da forma\((x,y)\), então sua função inversa\(f^{−1}(x)\) é o conjunto de pares ordenados\((y,x)\).
Então, se um ponto\((a,b)\) está no gráfico de uma função\(f(x)\), então o par ordenado\((b,a)\) está no gráfico de\(f^{−1}(x)\). Veja a Figura 10.1.43.
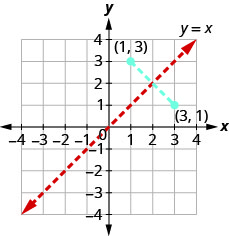
A distância entre quaisquer dois pares\((a,b)\)\((b,a)\) é cortada ao meio pela linha\(y=x\). Então, dizemos que os pontos são imagens espelhadas um do outro ao longo da linha\(y=x\).
Como cada ponto no gráfico de uma função\(f(x)\) é uma imagem espelhada de um ponto no gráfico de\(f^{−1}(x)\), dizemos que os gráficos são imagens espelhadas um do outro através da linha\(y=x\). Usaremos esse conceito para representar graficamente o inverso de uma função no próximo exemplo.
Gráfico, no mesmo sistema de coordenadas, o inverso da função um-para-um mostrada.
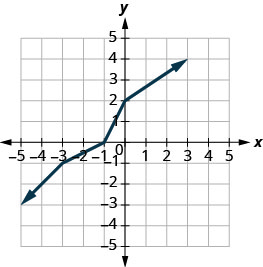
Solução:
Podemos usar pontos no gráfico para encontrar pontos no gráfico inverso. Alguns pontos no gráfico são:\((−5,−3),(−3,−1),(−1,0),(0,2),(3,4)\).
Então, a função inversa conterá os pontos:\((−3,−5),(−1,−3),(0,−1),(2,0),(4,3)\).
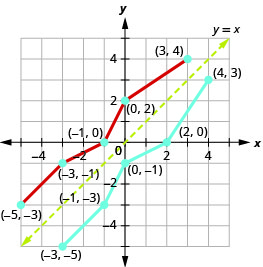
Observe como o gráfico da função original e o gráfico das funções inversas são imagens espelhadas ao longo da linha\(y=x\).
Gráfico, no mesmo sistema de coordenadas, o inverso da função um para um.
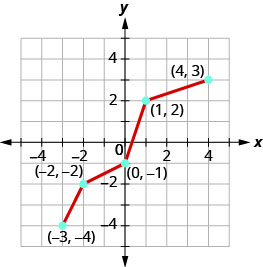
- Responda
-
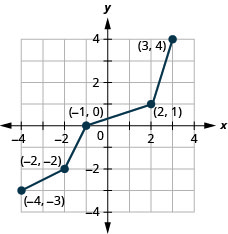
Figura 10.1.49
Gráfico, no mesmo sistema de coordenadas, o inverso da função um para um.
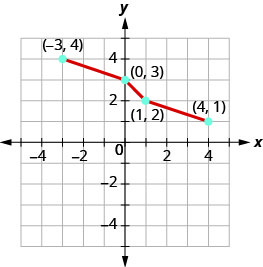
- Responda
-
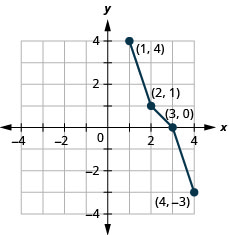
Figura 10.1.51
Quando começamos nossa discussão sobre uma função inversa, falamos sobre como a função inversa 'desfaz' o que a função original fez com um valor em seu domínio para voltar ao\(x\) valor original.

Funções inversas
\(f^{-1}(f(x))=x\), para todos\(x\) no domínio da\(f\)
\(f\left(f^{-1}(x)\right)=x\), para todos\(x\) no domínio da\(f^{-1}\)
Podemos usar essa propriedade para verificar se duas funções são inversas uma da outra.
Verifique\(f(x)=5x−1\) se\(g(x)=\frac{x+1}{5}\) são funções inversas.
Solução:
As funções são inversas uma da outra se\(g(f(x))=x\)\(f(g(x))=x\) e.
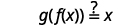 |
|
| Substitua\(5x-1\) para\(f(x)\). | 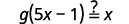 |
 |
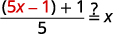 |
| Simplifique. | 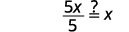 |
| Simplifique. | 
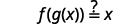
|
| Substituto\(\frac{x+1}{5}\) para\(g(x)\). | 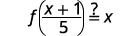 |
 |
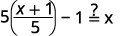 |
| Simplifique. | 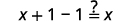 |
| Simplifique. |  |
Como ambas\(g(f(x))=x\)\(f(g(x))=x\) são verdadeiras, as funções\(f(x)=5x−1\) e\(g(x)=\frac{x+1}{5}\) são funções inversas. Ou seja, eles são inversos um do outro.
Verifique se as funções são funções inversas. \(f(x)=4 x-3\)\(g(x)=\frac{x+3}{4}\)e.
- Responda
-
\(g(f(x))=x\), e\(f(g(x))=x\), portanto, são inversas.
Verifique se as funções são funções inversas. \(f(x)=2 x+6\)e\(g(x)=\frac{x-6}{2}\)
- Responda
-
\(g(f(x))=x,\)e\(f(g(x))=x,\), portanto, são inversas.
Encontramos inversas de funções definidas por pares ordenados e de um gráfico. Agora veremos como encontrar um inverso usando uma equação algébrica. O método usa a ideia de que se\(f(x)\) for uma função individual com pares ordenados\((x,y)\), sua função inversa\(f^{−1}(x)\) é o conjunto de pares ordenados\((y,x)\).
Se invertermos o\(x\) e\(y\) na função e depois resolvermos para\(y\), obteremos nossa função inversa.
Encontre o inverso de\(f(x)=4 x+7\).
Solução:
| Etapa 1. Substituto\(y\) para\(f(x)\). | \(f(x)\)Substitua por\(y\). | \(\begin{aligned} f(x) &=4 x+7 \\ y &=4 x+7 \end{aligned}\) |
| Etapa 2: Troque as variáveis\(x\)\(y\) e. | \(x\)Substitua por\(y\) e depois\(y\) por\(x\). | \(x=4y+7\) |
| Etapa 3: Resolver\(y\). |
Subtraia\(7\) de cada lado. Divida por\(4\). |
\(x-7=4 y\) \(\frac{x-7}{4}=y\) |
| Etapa 4: Substitua\(f^{-1}(x)\) por\(y\). | \(y\)Substitua por\(f^{-1}(x)\). | \(\frac{x-7}{4}=f^{-1}(x)\) |
| Etapa 5: Verifique se as funções são inversas. |
Mostra\(f^{-1}(f(x))=x\) e\(f\left(f^{-1}(x)\right)=x\) |
\(\begin{aligned} f^{-1}(f(x)) & \stackrel{?}{=} x \\f^{-1}(4x+7)&\stackrel{?}{=}x\\ \frac{(4x+7)-7}{4}&\stackrel{?}{=}x \\ \frac{4x}{4}&\stackrel{?}{=}x\\x&=x \\ \\f(f^{-1}(x))&\stackrel{?}{=}x \\f \left(\frac{x-7}{4} \right)&\stackrel{?}{=}x \\ 4\left(\frac{x-7}{4} \right) + 7 &\stackrel{?}{=}x \\ x-7+7&\stackrel{?}{=}x \\x&=x \end{aligned}\) |
Encontre o inverso da função\(f(x)=5x-3\).
- Responda
-
\(f^{-1}(x)=\frac{x+3}{5}\)
Encontre o inverso da função\(f(x)=8 x+5\).
- Responda
-
\(f^{-1}(x)=\frac{x-5}{8}\)
Resumimos as etapas abaixo.
Como encontrar o inverso de uma função um-para-um
- Substituto\(y\) para\(f(x)\).
- Troque as variáveis\(x\)\(y\) e.
- Resolver para\(y\).
- Substituto\(f^{−1}(x)\) para\(y\).
- Verifique se as funções são inversas.
Encontre o inverso de\(f(x)=\sqrt[5]{2 x-3}\).
Solução:
\(f(x)=\sqrt[5]{2 x-3}\)
Substituto\(y\) para\(f(x)\).
\(y=\sqrt[5]{2 x-3}\)
Troque as variáveis\(x\)\(y\) e.
\(x=\sqrt[5]{2 y-3}\)
Resolver para\(y\).
\(\begin{aligned}(x)^{5} &=(\sqrt[5]{2 y-3})^{5} \\ x^{5} &=2 y-3 \\ x^{5}+3 &=2 y \\ \frac{x^{5}+3}{2} &=y \end{aligned}\)
Substituto\(f^{-1}(x)\) para\(y\).
\(f^{-1}(x)=\frac{x^{5}+3}{2}\)
Verifique se as funções são inversas.
\(\begin{array}{rr} {f^{-1}(f(x)) \stackrel{?}{=} x} & {f\left(f^{-1}(x)\right) \stackrel{?}{=} x} \\ {f^{-1}(\sqrt[5]{2x-3})\stackrel{?}{=}x}&{f\left(\frac{x^{5}+3}{2} \right)}\stackrel{?}{=}x \\ {\frac{(\sqrt[5]{2x-3})^{5}+3}{2}\stackrel{?}{=}x}&{\sqrt[5]{2\left(\frac{x^{5}+3}{2} \right)-3}\stackrel{?}{=}x} \\ {\frac{2x-3+3}{2}\stackrel{?}{=}x}&{\sqrt[5]{x^{5}+3-3}\stackrel{?}{=}x}\\ {\frac{2x}{2}\stackrel{?}{=}x}&{\sqrt[5]{x^{5}}\stackrel{?}{=}x} \\ {x=x}&{x=x} \end{array}\)
Encontre o inverso da função\(f(x)=\sqrt[5]{3 x-2}\).
- Responda
-
\(f^{-1}(x)=\frac{x^{5}+2}{3}\)
Encontre o inverso da função\(f(x)=\sqrt[4]{6 x-7}\).
- Responda
-
\(f^{-1}(x)=\frac{x^{4}+7}{6}\)
Conceitos-chave
- Composição de funções: A composição de funções\(f\) e\(g\), é escrita\(f∘g\) e é definida por
\((f \circ g)(x)=f(g(x))\)
Lemos\(f(g(x))\) a partir\(f\)\(g\) de\(x\). - Teste de linha horizontal: se cada linha horizontal cruzar o gráfico de uma função em no máximo um ponto, é uma função individual.
- Inverso de uma função definida por pares ordenados: Se\(f(x)\) for uma função individual cujos pares ordenados são da forma\((x,y)\), então sua função inversa\(f^{−1}(x)\) é o conjunto de pares ordenados\((y,x)\).
- Funções inversas: Para cada um\(x\) no domínio da função individual\(f\) e\(f^{−1}\),
\(f^{-1}(f(x))=x\)
\(f\left(f^{-1}(x)\right)=x\) - Como encontrar o inverso de uma função um-para-um:
- Substituto\(y\) para\(f(x)\).
- Troque as variáveis\(x\)\(y\) e.
- Resolver para\(y\).
- Substituto\(f^{−1}(x)\) para\(y\).
- Verifique se as funções são inversas.
Glossário
- função um para um
- Uma função é individual se cada valor no intervalo tiver exatamente um elemento no domínio. Para cada par ordenado na função, cada\(y\) valor -é combinado com apenas um\(x\) valor.


