9.9: Resolver desigualdades quadráticas

Last updated
Save as PDF

Page ID: 183508

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Ao final desta seção, você poderá:

Resolva desigualdades quadráticas graficamente
Resolva desigualdades quadráticas algebricamente

Antes de começar, faça este teste de prontidão.

Resolver:$2x−3=0$.
Se você perdeu esse problema, revise o Exemplo 2.2.
Resolver:$2y^{2}+y=15$.
Se você perdeu esse problema, consulte o Exemplo 6.45.
Resolver$\frac{1}{x^{2}+2 x-8}>0$
Se você perdeu esse problema, consulte o Exemplo 7.56.

Aprendemos como resolver desigualdades lineares e racionais anteriormente. Algumas das técnicas que usamos para resolvê-las eram as mesmas e outras eram diferentes. Agora aprenderemos a resolver desigualdades que têm uma expressão quadrática. Usaremos algumas das técnicas de resolução de desigualdades lineares e racionais, bem como equações quadráticas. Resolveremos as desigualdades quadráticas de duas maneiras: graficamente e algebricamente.

Resolva desigualdades quadráticas graficamente

Uma equação quadrática está na forma padrão quando escrita como$ax^{2}+bx+c=0$. Se substituirmos o sinal de igual por um sinal de desigualdade, teremos uma desigualdade quadrática na forma padrão.

Definição$\PageIndex{1}$: Quadratic Inequality

Uma desigualdade quadrática é uma desigualdade que contém uma expressão quadrática. A forma padrão de uma desigualdade quadrática está escrita:

$\begin{array}{ll}{a x^{2}+b x+c<0} & {a x^{2}+b x+c \leq 0} \\ {a x^{2}+b x+c>0} & {a x^{2}+b x+c \geq 0}\end{array}$

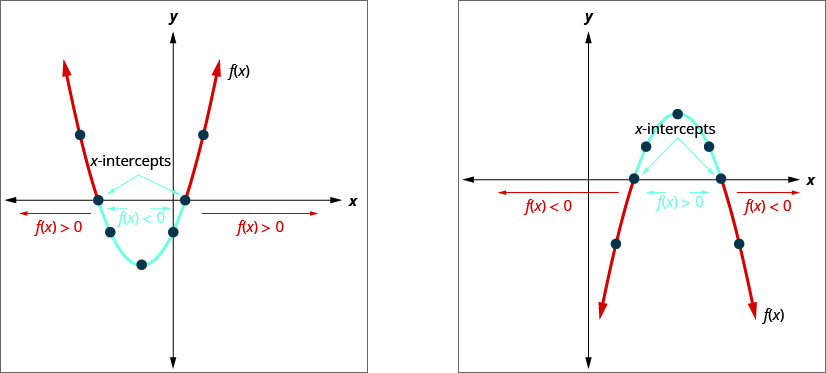
O gráfico de uma função quadrática$f(x)=a x^{2}+b x+c=0$ é uma parábola. Quando perguntamos quando é$a x^{2}+b x+c<0$, estamos perguntando quando é$f(x)<0$. Queremos saber quando a parábola está abaixo do$x$ eixo y.

Quando perguntamos quando é$a x^{2}+b x+c>0$, estamos perguntando quando é$f(x)>0$. Queremos saber quando a parábola está acima do$y$ eixo y.

O primeiro gráfico é uma parábola voltada para cima, f de x, em um plano de coordenadas x y. À esquerda da função, f de x é maior que 0. Entre os interceptos x, f de x é menor que 0. À direita da função, f de x é maior que 0. O segundo gráfico é uma parábola voltada para baixo, f de x, em um plano coordenado x y. À esquerda da função, f de x é menor que 0. Entre os interceptos x, f de x é maior que 0. À direita da função, f de x é menor que 0. — Figura 9.8.1

Exemplo$\PageIndex{1}$: How to Solve a Quadratic Inequality Graphically

Resolva$x^{2}−6x+8<0$ graficamente. Escreva a solução em notação de intervalo.

Solução:

Etapa 1: Escreva a desigualdade quadrática na forma padrão.

A desigualdade está na forma padrão.

$x^{2}-6 x+8<0$

Etapa 2: Faça um gráfico da função$f(x)=a x^{2}+b x+c$ usando propriedades ou transformações.

Vamos representar graficamente usando as propriedades.

$f(x)=x^{2}-6 x+8$

Veja$a$ na equação.

$\color{red}{a=1, b=-6, c=8}$

$f(x)=x^{2}-6 x+8$

Como$a$ é positivo, a parábola se abre para cima.

A parábola se abre para cima.

$f(x)=x^{2}-6 x+8$

O eixo de simetria é a linha$x=-\frac{b}{2 a}$.

Eixo de simetria

$x=-\frac{b}{2 a}$

$\begin{array}{l}{x=-\frac{(-6)}{2 \cdot 1}} \\ {x=3}\end{array}$

O eixo de simetria é a linha$x=3$.

O vértice está no eixo de simetria. $x=3$Substitua na função.

Vértice

$\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8} \\ {f(3)=-1}\end{array}$

O vértice é$(3,-1)$.

Nós encontramos$f(0)$

$y$-interceptar

$\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8} \\ {f(0)=8}\end{array}$

O$y$ intercepto -é$(0.8)$.

Usamos o eixo de simetria para encontrar um ponto simétrico ao$y$ intercepto. O$y$ intercepto -é a$3$ unidade à esquerda do eixo de simetria,$x=3$. Uma$3$ unidade de ponto à direita do eixo de simetria tem$x=6$.

Ponto simétrico a$y$ -intercepto

A questão é$(6,8)$.

Nós resolvemos$f(x)=0$.

$x$-intercepta

Podemos resolver essa equação quadrática fatorando.

$\begin{aligned} f(x) &=x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}(x-2)(x-4) \\ x &=2 \text { or } x=4 \end{aligned}$

As$x$ interceptações -são$(2,0)$$(4,0)$ e.

Representamos graficamente o vértice, os interceptos e o ponto simétrico ao$y$ intercepto. Conectamos esses$5$ pontos para esboçar a parábola.

Etapa 3: Determine a solução a partir do gráfico.

$x^{2}-6 x+8<0$

A desigualdade solicita os valores dos$x$ quais tornam a função menor que$0$. Quais valores de$x$ formam a parábola abaixo do$x$ eixo -.

Não incluímos os valores$2$,$4$ pois a desigualdade é menor do que apenas.

A solução, em notação de intervalo, é$(2,4)$.

Exercício$\PageIndex{1}$

Resolva$x^{2}+2 x-8<0$ graficamente
Escreva a solução em notação de intervalo

Responda

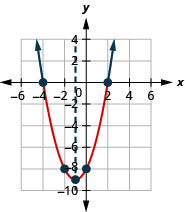
$Esta figura mostra uma parábola que se abre para cima no plano de coordenadas x y. Tem um vértice de (menos 2, menos 9), intercepto y de (0, 8) e eixo de simetria mostrado em x é igual a menos 2.$
Figura 9.8.4
$(-4,2)$

Exercício$\PageIndex{2}$

Resolva$x^{2}-8 x+12 \geq 0$ graficamente
Escreva a solução em notação de intervalo

Responda

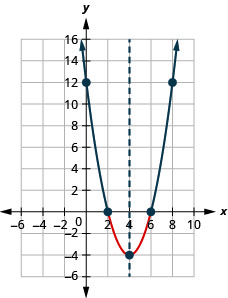
$Esta figura mostra uma parábola que se abre para cima no plano de coordenadas x y. Tem um vértice de (4, menos 4) e interceptos x de (2, 0) e (6, 0).$
Figura 9.8.5
$(-\infty, 2] \cup[6, \infty)$

Listamos as etapas a serem seguidas para resolver graficamente uma desigualdade quadrática.

Resolva graficamente uma desigualdade quadrática

Escreva a desigualdade quadrática na forma padrão.
Faça um gráfico da função$f(x)=ax^{2}+bx+c$.
Determine a solução a partir do gráfico.

No último exemplo, a parábola se abriu para cima e no próximo exemplo, ela se abre para baixo. Em ambos os casos, estamos procurando a parte da parábola que está abaixo do$x$ eixo -, mas observamos como a posição da parábola afeta a solução.

Exemplo$\PageIndex{2}$

Resolva$-x^{2}-8 x-12 \leq 0$ graficamente. Escreva a solução em notação de intervalo.

Solução:

Tabela 9.8.1
A desigualdade quadrática na forma padrão.	$-x^{2}-8 x-12 \leq 0$
Faça um gráfico da função $f(x)=-x^{2}-8 x-12$	A parábola se abre para baixo. $.$ Figura 9.8.6
Encontre a linha de simetria.	$\begin{array}{l}{x=-\frac{b}{2 a}} \\ {x=-\frac{-8}{2(-1)}} \\ {x=-4}\end{array}$
Encontre o vértice.	$\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ f(-4) &=-(-4)^{2}-8(-4)-12 \\ f(-4) &=-16+32-12 \\ & f(-4)=4 \end{aligned}$ Vértice$(-4,4)$
Encontre as$x$ interceptações -. Deixe$f(x)=0$.	$\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ 0 &=-x^{2}-8 x-12 \end{aligned}$
Fator: Use a propriedade Zero Product.	$\begin{array}{l}{0=-1(x+6)(x+2)} \\ {x=-6 \quad x=-2}\end{array}$
Faça um gráfico da parábola.	$x$-intercepta$(-6,0), (-2.0)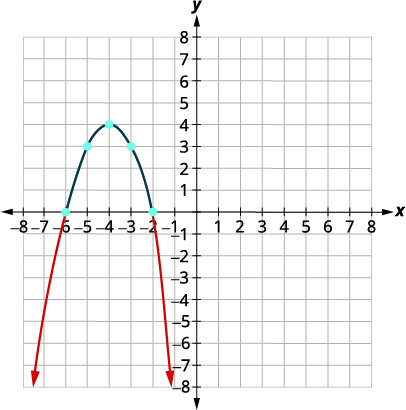$ $.$ Figura 9.8.7
Determine a solução a partir do gráfico. Incluímos os$x$ interceptos -porque a desigualdade é “menor ou igual a”.	$(-\infty,-6] \cup[-2, \infty)$

Exercício$\PageIndex{3}$

Resolva$-x^{2}-6 x-5>0$ graficamente
Escreva a solução em notação de intervalo

Responda

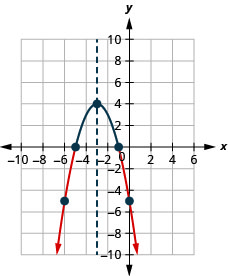
$Uma parábola voltada para baixo no plano de coordenadas x y. Tem um vértice de (menos 3, 4), um intercepto y em (0, menos 5) e um eixo de simetria mostrado em x é igual a menos 3.$
Figura 9.8.8
$(-5,-1)$

Exercício$\PageIndex{4}$

Resolva$−x^{2}+10x−16≤0$ graficamente
Escreva a solução em notação de intervalo

Responda

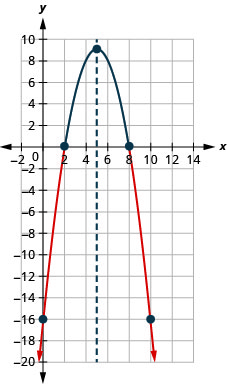
$Uma parábola voltada para baixo no plano de coordenadas x y. Tem um vértice de (5, 9), um intercepto y em (0, menos 16) e um eixo de simetria de x igual a 5.$
Figura 9.8.9
$(-\infty, 2] \cup[8, \infty)$

Resolva desigualdades quadráticas algebricamente

O método algébrico que usaremos é muito semelhante ao método que usamos para resolver desigualdades racionais. Encontraremos os pontos críticos para a desigualdade, que serão as soluções para a equação quadrática relacionada. Lembre-se de que uma expressão polinomial só pode mudar de sinal quando a expressão é zero.

Usaremos os pontos críticos para dividir a reta numérica em intervalos e depois determinar se a expressão quadrática será positiva ou negativa no intervalo. Em seguida, determinamos a solução para a desigualdade.

Exemplo$\PageIndex{3}$: How to Solve Quadratic Inequalities Algebraically

Resolva$x^{2}-x-12 \geq 0$ algebricamente. Escreva a solução em notação de intervalo.

Solução:

Tabela 9.8.2
Etapa 1: Escreva a desigualdade quadrática na forma padrão.	A desigualdade está na forma padrão.	$x^{2}-x-12 \geq 0$
Etapa 2: Determine os pontos críticos — as soluções para a equação quadrática relacionada.	Altere o sinal de desigualdade para um sinal de igual e, em seguida, resolva a equação.	$\begin{array}{c}{x^{2}-x-12=0} \\ {(x+3)(x-4)=0} \\ {x+3=0 \quad x-4=0} \\ {x=-3 \quad x=4}\end{array}$
Etapa 3: Use os pontos críticos para dividir a reta numérica em intervalos.	Use$-3$ e$4$ para dividir a reta numérica em intervalos.	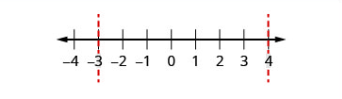$Captura de tela (4) .png$
Etapa 4: Acima da linha numérica, mostre o sinal de cada expressão quadrática usando pontos de teste de cada intervalo substituídos pela desigualdade original.	Teste: $x=-5$ $x=0$ $x=5$	$\begin{array}{ccc}{x^{2}-x-12} & {x^{2}-x-12} & {x^{2}-x-12} \\ {(-5)^{2}-(-5)-12} & {0^{2}-0-12} & {5^{2}-5-12} \\ {18} & {-12} & {8}\end{array}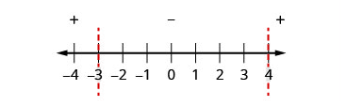$ $Captura de tela (5) .png$ Figura 9.8.11
Etapa 5: Determine os intervalos em que a desigualdade está correta. Escreva a solução em notação de intervalo.	$x^{2}-x-12 \geq 0$ A desigualdade é positiva no primeiro e no último intervalo e é igual$0$ nos pontos$-4,3$.	A solução, em notação de intervalo, é$(-\infty,-3] \cup[4, \infty)$.

Exercício$\PageIndex{5}$

Resolva$x^{2}+2x−8≥0$ algebricamente. Escreva a solução em notação de intervalo.

Responda: $(-\infty,-4] \cup[2, \infty)$

Exercício$\PageIndex{6}$

Resolva$x^{2}−2x−15≤0$ algebricamente. Escreva a solução em notação de intervalo.

Responda: $[-3,5]$

Neste exemplo, como a expressão$x^{2}−x−12$ influencia bem, também podemos encontrar o sinal em cada intervalo da mesma forma que fizemos quando resolvemos desigualdades racionais. Encontramos o sinal de cada um dos fatores e depois o sinal do produto. Nossa linha numérica ficaria assim:

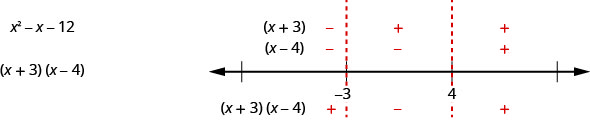
A figura mostra a expressão x ao quadrado menos x menos 12 fatorada à quantidade de x mais 3 vezes a quantidade de x menos 4. A imagem mostra uma linha numérica mostrando linhas pontilhadas em menos 3 e 4. Mostra os sinais da quantidade x mais 3 como negativa, positiva, positiva e os sinais da quantidade x menos 4 como negativa, negativa, positiva. Abaixo da linha numérica, mostra a quantidade x mais 3 vezes a quantidade x menos 4 com os sinais positivo, negativo, positivo. — Figura 9.8.12

O resultado é o mesmo que encontramos usando o outro método.

Resumimos as etapas aqui.

Resolva uma desigualdade quadrática algebricamente

Escreva a desigualdade quadrática na forma padrão.
Determine os pontos críticos — as soluções para a equação quadrática relacionada.
Use os pontos críticos para dividir a reta numérica em intervalos.
Acima da linha numérica, mostre o sinal de cada expressão quadrática usando pontos de teste de cada intervalo substituídos pela desigualdade original.
Determine os intervalos em que a desigualdade está correta. Escreva a solução em notação de intervalo.

Exemplo$\PageIndex{4}$

Resolva$x^{2}+6x−7≥0$ algebricamente. Escreva a solução em notação de intervalo.

Solução:

Tabela 9.8.3
Escreva a desigualdade quadrática na forma padrão.	$-x^{2}+6 x-7 \geq 0$
Multiplique os dois lados da desigualdade por$-1$. Lembre-se de reverter o sinal de desigualdade.	$x^{2}-6 x+7 \leq 0$
Determine os pontos críticos resolvendo a equação quadrática relacionada.	$x^{2}-6 x+7=0$
Escreva a fórmula quadrática.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
Em seguida, substitua os valores de$a, b, c$.	$x=\frac{-(-6) \pm \sqrt{(-6)^{2}-4 \cdot 1 \cdot(7)}}{2 \cdot 1}$
Simplifique.	$x=\frac{6 \pm \sqrt{8}}{2}$
Simplifique o radical.	$x=\frac{6 \pm 2 \sqrt{2}}{2}$
Remova o fator comum,$2$.	$\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ {x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \approx 1.6}\quad\quad\:\:\: x\approx 4.4\end{array}$
Use os pontos críticos para dividir a reta numérica em intervalos. Teste os números de cada intervalo na desigualdade original.	$.$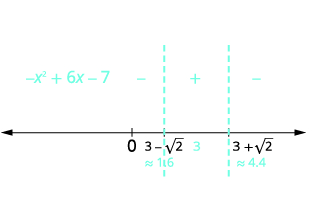
Determine os intervalos em que a desigualdade está correta. Escreva a solução em notação de intervalo.	$-x^{2}+6 x-7 \geq 0$no intervalo intermediário$[3-\sqrt{2}, 3+\sqrt{2}]$

Exercício$\PageIndex{7}$

Resolva$−x^{2}+2x+1≥0$ algebricamente. Escreva a solução em notação de intervalo.

Responda: $[-1-\sqrt{2},-1+\sqrt{2}]$

Exercício$\PageIndex{8}$

Resolva$−x^{2}+8x−14<0$ algebricamente. Escreva a solução em notação de intervalo.

Responda: $(-\infty, 4-\sqrt{2}) \cup(4+\sqrt{2}, \infty)$

As soluções das desigualdades quadráticas em cada um dos exemplos anteriores eram um intervalo ou a união de dois intervalos. Isso resultou do fato de que, em cada caso, encontramos duas soluções para a equação quadrática correspondente$ax^{2}+bx+c=0$. Essas duas soluções então nos deram as duas$x$ interceptações para o gráfico ou os dois pontos críticos para dividir a reta numérica em intervalos.

Isso se correlaciona com nossa discussão anterior sobre o número e o tipo de soluções para uma equação quadrática usando o discriminante.

Para uma equação quadrática do formulário$ax^{2}+bc+c=0, a≠0$.

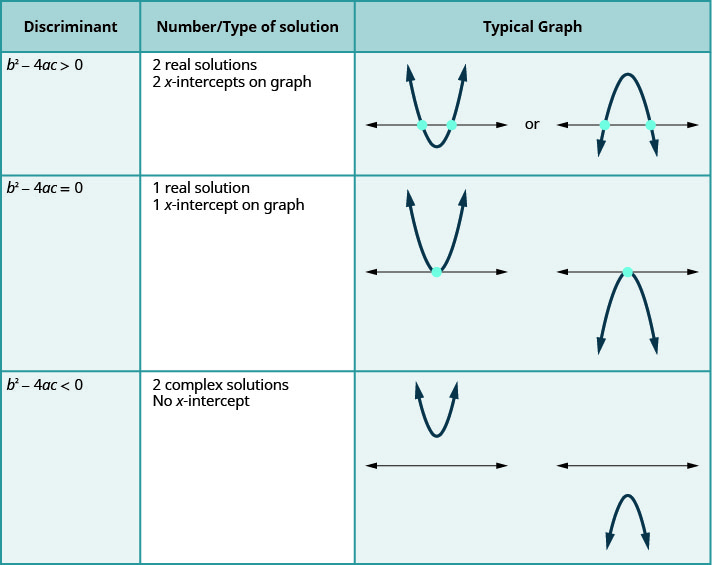
A figura é uma tabela com 3 colunas. A coluna 1 é rotulada como discriminante, a coluna 2 é o número/tipo de solução e a coluna 3 é o gráfico típico. Lendo as colunas, se b ao quadrado menos 4 vezes a vezes c for maior que 0, haverá 2 soluções reais porque há 2 interceptos x no gráfico. A imagem de um gráfico típico, uma parábola ascendente ou descendente com 2 interceptos-x. Se o discriminante b ao quadrado menos 4 vezes a vezes c for igual a 0, então há 1 solução real porque há 1 intercepto x no gráfico. A imagem do gráfico típico é uma parábola voltada para cima ou para baixo que tem um vértice no eixo x em vez de atravessá-lo. Se o discriminante b ao quadrado menos 4 vezes a vezes c for menor que 0, há 2 soluções complexas porque não há intercepto x. A imagem do gráfico típico mostra uma parábola voltada para cima ou para baixo que não cruza o eixo x. — Figura 9.8.14

A última linha da tabela nos mostra quando as parábolas nunca cruzam o$x$ eixo y. Usando a Fórmula Quadrática para resolver a equação quadrática, o radicando é negativo. Temos duas soluções complexas.

No próximo exemplo, as soluções de desigualdade quadrática resultarão da complexidade da solução da equação quadrática.

Exemplo$\PageIndex{5}$

Resolva, escrevendo qualquer solução em notação de intervalo:

$x^{2}-3 x+4>0$
$x^{2}-3 x+4 \leq 0$

Solução:

uma.

Tabela 9.8.4
Escreva a desigualdade quadrática na forma padrão.	$-x^{2}-3 x+4>0$
Determine os pontos críticos resolvendo a equação quadrática relacionada.	$x^{2}-3 x+4=0$
Escreva a fórmula quadrática.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
Em seguida, substitua os valores de$a, b, c$.	$x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \cdot 1 \cdot(4)}}{2 \cdot 1}$
Simplifique.	$x=\frac{3 \pm \sqrt{-7}}{2}$
Simplifique o radicando.	$x=\frac{3 \pm \sqrt{7 i}}{2}$
As soluções complexas nos dizem que a parábola não intercepta o$x$ eixo y. Além disso, a parábola se abre para cima. Isso nos diz que a parábola está completamente acima do$x$ eixo y.	Soluções complexas 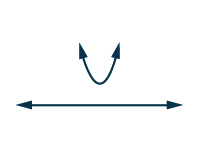$.$ Figura 9.8.15

Devemos encontrar a solução para$x^{2}−3x+4>0$. Como todos os valores$x$ do gráfico estão acima do$x$ eixo -, todos os valores de$x$ tornam a desigualdade verdadeira. Na notação de intervalo, escrevemos$(−∞,∞)$.

b. Escreva a desigualdade quadrática na forma padrão.

$x^{2}-3 x+4 \leq 0$

Determine os pontos críticos resolvendo a equação quadrática relacionada.

$x^{2}-3 x+4=0$

Como a equação quadrática correspondente é a mesma da parte (a), a parábola será a mesma. A parábola se abre para cima e está completamente acima do$x$ eixo -— nenhuma parte dela está abaixo do$x$ eixo -.

Devemos encontrar a solução para$x^{2}−3x+4≤0$. Como todos os valores$x$ do gráfico nunca estão abaixo do$x$ eixo -, nenhum valor de$x$ torna a desigualdade verdadeira. Não há solução para a desigualdade.

Exercício$\PageIndex{9}$

Resolva e escreva qualquer solução em notação de intervalo:

$-x^{2}+2 x-4 \leq 0$
$-x^{2}+2 x-4 \geq 0$

Responda

$(-\infty, \infty)$
sem solução

Exercício$\PageIndex{10}$

Resolva e escreva qualquer solução em notação de intervalo:

$x^{2}+3 x+3<0$
$x^{2}+3 x+3>0$

Responda

sem solução
$(-\infty, \infty)$

Conceitos-chave

Resolva graficamente uma desigualdade quadrática
1. Escreva a desigualdade quadrática na forma padrão.
2. Faça um gráfico da função$f(x)=ax^{2}+bx+c$ usando propriedades ou transformações.
3. Determine a solução a partir do gráfico.
Como resolver uma desigualdade quadrática algebricamente
1. Escreva a desigualdade quadrática na forma padrão.
2. Determine os pontos críticos — as soluções para a equação quadrática relacionada.
3. Use os pontos críticos para dividir a reta numérica em intervalos.
4. Acima da linha numérica, mostre o sinal de cada expressão quadrática usando pontos de teste de cada intervalo substituídos pela desigualdade original.
5. Determine os intervalos em que a desigualdade está correta. Escreva a solução em notação de intervalo.

Glossário

desigualdade quadrática: Uma desigualdade quadrática é uma desigualdade que contém uma expressão quadrática.

A desigualdade quadrática na forma padrão.	\(-x^{2}-8 x-12 \leq 0\)
Faça um gráfico da função \(f(x)=-x^{2}-8 x-12\)	A parábola se abre para baixo. $.$ Figura 9.8.6
Encontre a linha de simetria.	\(\begin{array}{l}{x=-\frac{b}{2 a}} \\ {x=-\frac{-8}{2(-1)}} \\ {x=-4}\end{array}\)
Encontre o vértice.	\(\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ f(-4) &=-(-4)^{2}-8(-4)-12 \\ f(-4) &=-16+32-12 \\ & f(-4)=4 \end{aligned}\) Vértice\((-4,4)\)
Encontre as\(x\) interceptações -. Deixe\(f(x)=0\).	\(\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ 0 &=-x^{2}-8 x-12 \end{aligned}\)
Fator: Use a propriedade Zero Product.	\(\begin{array}{l}{0=-1(x+6)(x+2)} \\ {x=-6 \quad x=-2}\end{array}\)
Faça um gráfico da parábola.	\(x\)-intercepta\((-6,0), (-2.0)\) $.$ Figura 9.8.7
Determine a solução a partir do gráfico. Incluímos os\(x\) interceptos -porque a desigualdade é “menor ou igual a”.	\((-\infty,-6] \cup[-2, \infty)\)

Escreva a desigualdade quadrática na forma padrão.	\(-x^{2}+6 x-7 \geq 0\)
Multiplique os dois lados da desigualdade por\(-1\). Lembre-se de reverter o sinal de desigualdade.	\(x^{2}-6 x+7 \leq 0\)
Determine os pontos críticos resolvendo a equação quadrática relacionada.	\(x^{2}-6 x+7=0\)
Escreva a fórmula quadrática.	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Em seguida, substitua os valores de\(a, b, c\).	\(x=\frac{-(-6) \pm \sqrt{(-6)^{2}-4 \cdot 1 \cdot(7)}}{2 \cdot 1}\)
Simplifique.	\(x=\frac{6 \pm \sqrt{8}}{2}\)
Simplifique o radical.	\(x=\frac{6 \pm 2 \sqrt{2}}{2}\)
Remova o fator comum,\(2\).	\(\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ {x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \approx 1.6}\quad\quad\:\:\: x\approx 4.4\end{array}\)
Use os pontos críticos para dividir a reta numérica em intervalos. Teste os números de cada intervalo na desigualdade original.	$.$
Determine os intervalos em que a desigualdade está correta. Escreva a solução em notação de intervalo.	\(-x^{2}+6 x-7 \geq 0\)no intervalo intermediário\([3-\sqrt{2}, 3+\sqrt{2}]\)

Escreva a desigualdade quadrática na forma padrão.	\(-x^{2}-3 x+4>0\)
Determine os pontos críticos resolvendo a equação quadrática relacionada.	\(x^{2}-3 x+4=0\)
Escreva a fórmula quadrática.	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Em seguida, substitua os valores de\(a, b, c\).	\(x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \cdot 1 \cdot(4)}}{2 \cdot 1}\)
Simplifique.	\(x=\frac{3 \pm \sqrt{-7}}{2}\)
Simplifique o radicando.	\(x=\frac{3 \pm \sqrt{7 i}}{2}\)
As soluções complexas nos dizem que a parábola não intercepta o\(x\) eixo y. Além disso, a parábola se abre para cima. Isso nos diz que a parábola está completamente acima do\(x\) eixo y.	Soluções complexas $.$ Figura 9.8.15

Definição\(\PageIndex{1}\): Quadratic Inequality

Exemplo\(\PageIndex{1}\): How to Solve a Quadratic Inequality Graphically

Exercício\(\PageIndex{1}\)

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{2}\)

Exercício\(\PageIndex{3}\)

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{3}\): How to Solve Quadratic Inequalities Algebraically

Exercício\(\PageIndex{5}\)

Exercício\(\PageIndex{6}\)

Exemplo\(\PageIndex{4}\)

Exercício\(\PageIndex{7}\)

Exercício\(\PageIndex{8}\)

Exemplo\(\PageIndex{5}\)

Exercício\(\PageIndex{9}\)

Exercício\(\PageIndex{10}\)

Etapa 1: Escreva a desigualdade quadrática na forma padrão.	A desigualdade está na forma padrão.	\(x^{2}-x-12 \geq 0\)
Etapa 2: Determine os pontos críticos — as soluções para a equação quadrática relacionada.	Altere o sinal de desigualdade para um sinal de igual e, em seguida, resolva a equação.	\(\begin{array}{c}{x^{2}-x-12=0} \\ {(x+3)(x-4)=0} \\ {x+3=0 \quad x-4=0} \\ {x=-3 \quad x=4}\end{array}\)
Etapa 3: Use os pontos críticos para dividir a reta numérica em intervalos.	Use\(-3\) e\(4\) para dividir a reta numérica em intervalos.	$Captura de tela (4) .png$
Etapa 4: Acima da linha numérica, mostre o sinal de cada expressão quadrática usando pontos de teste de cada intervalo substituídos pela desigualdade original.	Teste: \(x=-5\) \(x=0\) \(x=5\)	\(\begin{array}{ccc}{x^{2}-x-12} & {x^{2}-x-12} & {x^{2}-x-12} \\ {(-5)^{2}-(-5)-12} & {0^{2}-0-12} & {5^{2}-5-12} \\ {18} & {-12} & {8}\end{array}\) $Captura de tela (5) .png$ Figura 9.8.11
Etapa 5: Determine os intervalos em que a desigualdade está correta. Escreva a solução em notação de intervalo.	\(x^{2}-x-12 \geq 0\) A desigualdade é positiva no primeiro e no último intervalo e é igual\(0\) nos pontos\(-4,3\).	A solução, em notação de intervalo, é\((-\infty,-3] \cup[4, \infty)\).