Home
Idioma Portugues
Álgebra intermediária (OpenStax)
9: Equações e funções quadráticas
9.8: Representar graficamente funções quadráticas usando transformações

9.8: Representar graficamente funções quadráticas usando transformações

Last updated
Save as PDF

Page ID: 183531

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Ao final desta seção, você poderá:

Representar graficamente funções quadráticas da forma$f(x)=x^{2}+k$
Representar graficamente funções quadráticas da forma$f(x)=(x−h)^{2}$
Representar graficamente funções quadráticas da forma$f(x)=ax^{2}$
Representar graficamente funções quadráticas usando transformações
Encontre uma função quadrática em seu gráfico

Antes de começar, faça este teste de prontidão.

Faça um gráfico da função$f(x)=x^{2}$ traçando pontos.
Se você perdeu esse problema, consulte o Exemplo 3.54.
Fator completamente:$y^{2}−14y+49$.
Se você perdeu esse problema, consulte o Exemplo 6.24.
Fator completamente:$2x^{2}−16x+32$.
Se você perdeu esse problema, consulte o Exemplo 6.26.

Representar graficamente funções quadráticas do formulário$f(x)=x^{2}+k$

Na última seção, aprendemos como representar graficamente funções quadráticas usando suas propriedades. Outro método envolve começar com o gráfico básico$f(x)=x^{2}$ e “movê-lo” de acordo com as informações fornecidas na equação da função. Chamamos isso de representar graficamente funções quadráticas usando transformações.

No primeiro exemplo, representaremos graficamente a função$f(x)=x^{2}$ quadrática traçando pontos. Em seguida, veremos qual efeito a adição de uma constante$k$,, à equação terá no gráfico da nova função$f(x)=x^{2}+k$.

Exemplo$\PageIndex{1}$

Gráfico$f(x)=x^{2}$,$g(x)=x^{2}+2$, e$h(x)=x^{2}−2$ no mesmo sistema de coordenadas retangulares. Descreva qual efeito a adição de uma constante à função tem na parábola básica.

Solução:

Traçar pontos nos ajudará a ver o efeito das constantes no$f(x)=x^{2}$ gráfico básico. Preenchemos o gráfico para todas as três funções.

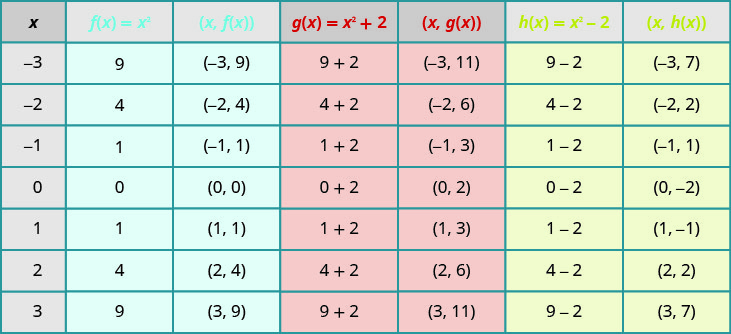
Uma tabela que mostra o efeito das constantes na função básica de x ao quadrado. A tabela tem sete colunas rotuladas x, f de x é igual a x ao quadrado, o par ordenado (x, f de x), g de x é igual a x ao quadrado mais 2, o par ordenado (x, g de x), h de x é igual a x ao quadrado menos 2 e o par ordenado (x, h de x). Na coluna x, os valores fornecidos são menos 3, menos 2, menos 1, 0, 1, 2 e 3. Na coluna f de x igual a x ao quadrado, os valores são 9, 4, 1, 0, 1, 4 e 9. Na coluna (x, f de x), os pares ordenados (menos 3, 9), (menos 2, 4), (menos 1, 1), (0, 0), (1, 1), (2, 4) e (3, 9) são fornecidos. A coluna g de x é igual a x ao quadrado mais 2 contém as expressões 9 mais 2, 4 mais 2, 1 mais 2, 0 mais 2, 1 mais 2, 4 mais 2 e 9 mais 2. A coluna (x, g de x) tem os pares ordenados de (menos 3, 11), (menos 2, 6), (menos 1, 3), (0, 2), (1, 3), (2, 6) e (3, 11). Na coluna h de x igual a x ao quadrado menos 2, as expressões dadas são 9 menos 2, 4 menos 2, 1 menos 2, 0 menos 2, 1 menos 2, 4 menos 2 e 9 menos 2. Na última coluna, (x, h de x), contém os pares ordenados (menos 3, 7), (menos 2, 2), (menos 1, menos 1), (0, menos 2), (1, menos 1), (2, 2) e (3, 7). — Figura 9.7.1

Os$g(x)$ valores são dois a mais do que os$f(x)$ valores. Além disso, os$h(x)$ valores são dois a menos que os$f(x)$ valores. Agora, representaremos graficamente todas as três funções no mesmo sistema de coordenadas retangulares.

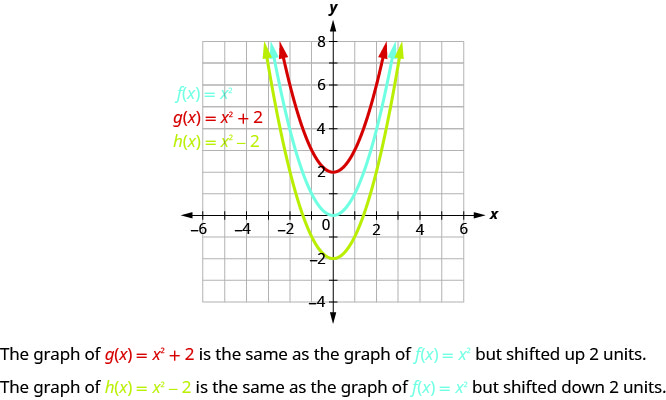
Esta figura mostra 3 parábolas de abertura ascendente no plano de coordenadas x y. O meio é o gráfico de f de x igual a x ao quadrado e tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A parábola superior foi movida 2 unidades para cima e a inferior foi movida para baixo 2 unidades. — Figura 9.7.2

O gráfico de$g(x)=x^{2}+2$ é o mesmo que o gráfico de$2$ unidades$f(x)=x^{2}$, mas deslocadas para cima.

O gráfico de$h(x)=x^{2}−2$ é o mesmo que o gráfico das$2$ unidades$f(x)=x^{2}$, mas deslocadas para baixo.

Exercício$\PageIndex{1}$

Gráfico$f(x)=x^{2}, g(x)=x^{2}+1,$ e$h(x)=x^{2}-1$ no mesmo sistema de coordenadas retangulares.
Descreva qual efeito a adição de uma constante à função tem na parábola básica.

Responda

uma.

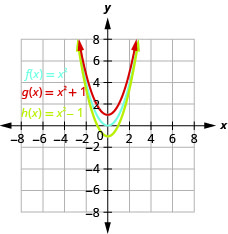
Esta figura mostra 3 parábolas de abertura ascendente no plano de coordenadas x y. O gráfico do meio é de f de x igual a x ao quadrado tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A curva superior foi movida para cima 1 unidade e a parte inferior foi movida para baixo 1 unidade. — Figura 9.7.3

b. O gráfico de$g(x)=x^{2}+1$ é o mesmo que o gráfico da$1$ unidade$f(x)=x^{2}$, mas deslocada para cima. O gráfico de$h(x)=x^{2}−1$ é o mesmo que o gráfico da$1$ unidade$f(x)=x^{2}$, mas deslocado para baixo.

Exercício$\PageIndex{2}$

Gráfico$f(x)=x^{2}, g(x)=x^{2}+6,$ e$h(x)=x^{2}-6$ no mesmo sistema de coordenadas retangulares.
Descreva qual efeito a adição de uma constante à função tem na parábola básica.

Responda

uma.

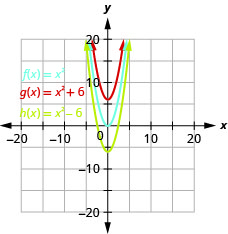
Esta figura mostra 3 parábolas de abertura ascendente no plano de coordenadas x y. A curva do meio é o gráfico de f de x igual a x ao quadrado e tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A curva superior foi movida 6 unidades para cima e a inferior foi movida para baixo 6 unidades. — Figura 9.7.4

b. O gráfico de$h(x)=x^{2}+6$ é o mesmo que o gráfico de$6$ unidades$f(x)=x^{2}$, mas deslocadas para cima. O gráfico de$h(x)=x^{2}-6$ é o mesmo que o gráfico das$6$ unidades$f(x)=x^{2}$, mas deslocadas para baixo.

O último exemplo nos mostra que, para representar graficamente uma função quadrática da forma$f(x)=x^{2}+k$, pegamos o gráfico básico da parábola de$f(x)=x^{2}$ e o deslocamos verticalmente para cima$(k>0)$ ou para baixo$(k<0)$.

Essa transformação é chamada de mudança vertical.

Representar graficamente uma função quadrática do formulário$f(x)=x^{2}+k$ usando um deslocamento vertical

O gráfico de$f(x)=x^{2}+k$ desloca o gráfico das$k$ unidades$f(x)=x^{2}$ verticais.

Se$k>0$, desloque a parábola verticalmente para cima$k$ das unidades.
Se$k<0$, desloque a parábola verticalmente para baixo em$|k|$ unidades.

Agora que vimos o efeito da constante$k$, é fácil representar graficamente as funções da forma$f(x)=x^{2}+k$. Começamos com a parábola básica de$f(x)=x^{2}$ e depois a deslocamos para cima ou para baixo.

Pode ser útil praticar esboços$f(x)=x^{2}$ rapidamente. Conhecemos os valores e podemos esboçar o gráfico a partir daí.

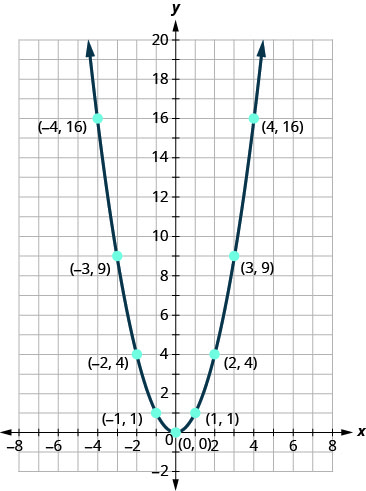
Esta figura mostra uma parábola de abertura ascendente no plano de coordenadas x y, com vértice (0, 0). Outros pontos na curva estão localizados em (menos 4, 16), (menos 3, 9), (menos 2, 4), (menos 1, 1), (1, 1), (2, 4), (3, 9) e (4, 16). — Figura 9.7.5

Depois de conhecermos essa parábola, será fácil aplicar as transformações. O próximo exemplo exigirá uma mudança vertical.

Exemplo$\PageIndex{2}$

Faça um gráfico$f(x)=x^{2}−3$ usando um deslocamento vertical.

Solução:

Tabela 9.7.1
Primeiro, desenhamos o gráfico de$f(x)=x^{2}$ na grade.	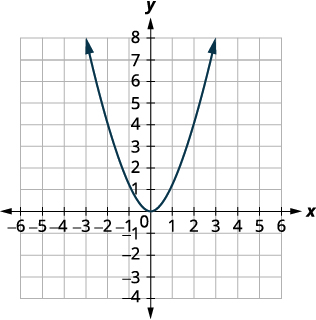$Esta figura mostra uma parábola de abertura ascendente no plano de coordenadas x y com um vértice de (0, 0) com outros pontos na curva localizados em (menos 1, 1) e (1, 1). É o gráfico de f de x igual a x ao quadrado.$
Determinar$k$.	$.$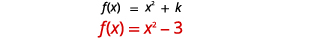
	$.$
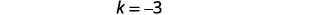Desloque o gráfico$f(x)=x^{2}$ para baixo$3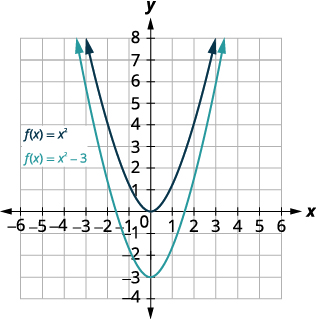$.	$Esta figura mostra 2 parábolas de abertura ascendente no plano de coordenadas x y. A curva superior é o gráfico de f de x igual a x ao quadrado que tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A curva inferior foi movida para baixo em 3 unidades.$

Exercício$\PageIndex{3}$

Faça um gráfico$f(x)=x^{2}−5$ usando um deslocamento vertical.

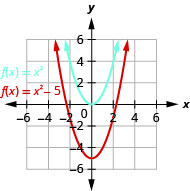
Responda: $Esta figura mostra 2 parábolas de abertura ascendente no plano de coordenadas x y. A curva superior é o gráfico de f de x igual a x ao quadrado e tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A curva inferior foi movida para baixo em 5 unidades.$
Figura 9.7.10

Exercício$\PageIndex{4}$

Faça um gráfico$f(x)=x^{2}+7$ usando um deslocamento vertical.

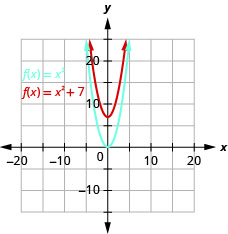
Responda: $Esta figura mostra 2 parábolas de abertura ascendente no plano de coordenadas x y. A curva inferior é o gráfico de f de x igual a x ao quadrado e tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A curva superior foi movida para cima em 7 unidades.$
Figura 9.7.11

Representar graficamente funções quadráticas do formulário$f(x)=(x-h)^{2}$

No primeiro exemplo, representamos graficamente a função$f(x)=x^{2}$ quadrática traçando pontos e depois vimos o efeito da adição de uma constante$k$ à função no gráfico resultante da nova função$f(x)=x^{2}+k$.

Agora vamos explorar o efeito de subtrair uma constante$h$,, de$x$ has no gráfico resultante da nova função$f(x)=(x−h)^{2}$.

Exemplo$\PageIndex{3}$

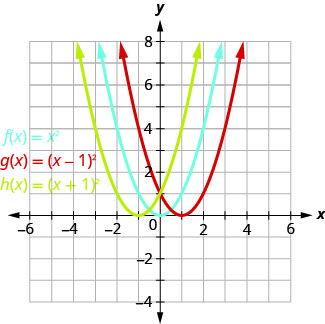
Gráfico$f(x)=x^{2}, g(x)=(x-1)^{2},$ e$h(x)=(x+1)^{2}$ no mesmo sistema de coordenadas retangulares. Descreva qual efeito a adição de uma constante à função tem na parábola básica.

Solução:

Traçar pontos nos ajudará a ver o efeito das constantes no$f(x)=x^{2}$ gráfico básico. Preenchemos o gráfico para todas as três funções.

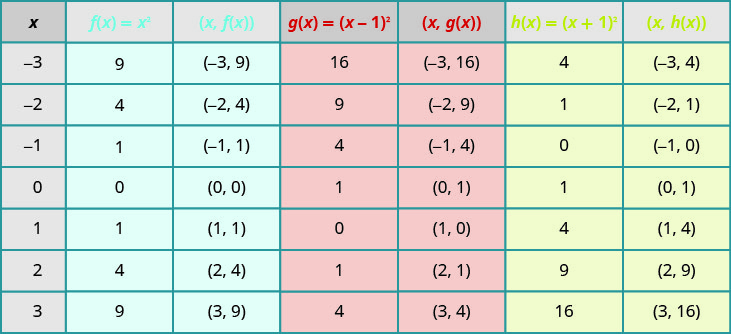
Os$g(x)$ valores e os$h(x)$ valores compartilham os números comuns$0, 1, 4, 9$, e$16$, mas são deslocados.

A figura diz na primeira linha que o gráfico de g de x é igual à quantidade x menos 1 quadrado é o mesmo que o gráfico de f de x é igual a x ao quadrado, mas deslocado para a direita 1 unidade. A segunda linha afirma que o gráfico de h de x é igual à quantidade x mais 1 ao quadrado é o mesmo que o gráfico de f de x é igual a x ao quadrado, mas deslocado para a esquerda em 1 unidade. A terceira linha da figura diz que g de x é igual à quantidade x menos 1 ao quadrado com uma seta abaixo apontando para a direita com 1 unidade escrita ao lado. Finalmente, dá h de x igual à quantidade de x mais 1 ao quadrado com uma seta abaixo apontando para a esquerda com 1 unidade escrita ao lado. — Figura 9.7.14

Exercício$\PageIndex{5}$

Gráfico$f(x)=x^{2}, g(x)=(x+2)^{2},$ e$h(x)=(x-2)^{2}$ no mesmo sistema de coordenadas retangulares.
Descreva qual efeito a adição de uma constante à função tem na parábola básica.

Responda

uma.

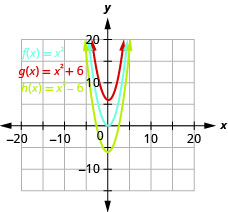
b. O gráfico de$g(x)=(x+2)^{2}$ é o mesmo que o gráfico das$2$ unidades à esquerda$f(x)=x^{2}$, mas deslocadas. O gráfico de$h(x)=(x−2)^{2}$ é o mesmo que o gráfico de,$f(x)=x^{2}$ mas desloca$2$ as unidades para a direita.

Exercício$\PageIndex{6}$

Gráfico$f(x)=x^{2}, g(x)=x^{2}+5,$ e$h(x)=x^{2}-5$ no mesmo sistema de coordenadas retangulares.
Descreva qual efeito a adição de uma constante à função tem na parábola básica.

Responda

uma.

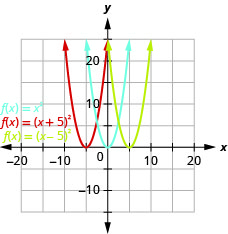
b. O gráfico de$g(x)=(x+5)^{2}$ é o mesmo que o gráfico das$5$ unidades à esquerda$f(x)=x^{2}$, mas deslocadas. O gráfico de$h(x)=(x-5)^{2}$ é o mesmo que o gráfico de$5$ unidades$f(x)=x^{2}$, mas deslocadas para a direita.

O último exemplo nos mostra que, para representar graficamente uma função quadrática da forma$f(x)=(x−h)^{2}$, pegamos o gráfico básico da parábola de$f(x)=x^{2}$ e o deslocamos para a esquerda$(h>0)$ ou para a direita$(h<0)$.

Essa transformação é chamada de mudança horizontal.

Representar graficamente uma função quadrática do formulário$f(x)=(x-h)^{2}$ usando um deslocamento horizontal

O gráfico de$f(x)=(x-h)^{2}$ desloca o gráfico das$h$ unidades$f(x)=x^{2}$ horizontais.

Se$h>0$, desloque a parábola horizontalmente para a$h$ esquerda.
Se$h<0$, desloque a parábola horizontalmente para a$|h|$ direita.

Agora que vimos o efeito da constante$h$, é fácil representar graficamente as funções da forma$f(x)=(x−h)^{2}$. Começamos com a parábola básica de$f(x)=x^{2}$ e depois a deslocamos para a esquerda ou para a direita.

O próximo exemplo exigirá uma mudança horizontal.

Exemplo$\PageIndex{4}$

Faça um gráfico$f(x)=(x−6)^{2}$ usando um deslocamento horizontal.

Solução:

Tabela 9.7.2
Primeiro, desenhamos o gráfico de$f(x)=x^{2}$ na grade.	$.$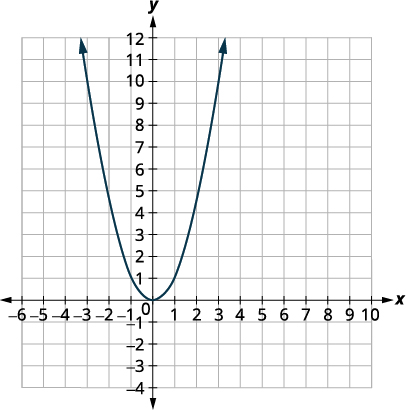
Determinar$h$.	$.$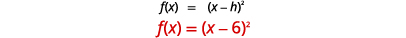
	$.$
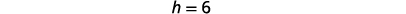Desloque o gráfico$f(x)=x^{2}$ para as$6$ unidades certas.	$.$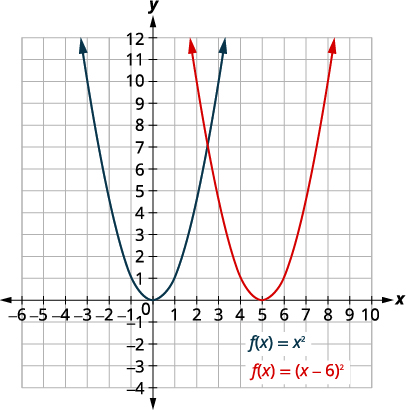

Exercício$\PageIndex{7}$

Faça um gráfico$f(x)=(x−4)^{2}$ usando um deslocamento horizontal.

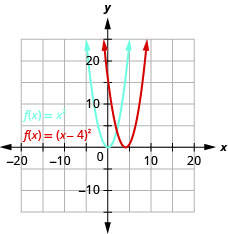
Responda: $Esta figura mostra 2 parábolas de abertura ascendente no plano de coordenadas x y. A curva esquerda é o gráfico de f de x igual a x ao quadrado que tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A curva direita foi movida 4 unidades para a direita.$
Figura 9.7.21

Exercício$\PageIndex{8}$

Faça um gráfico$f(x)=(x+6)^{2}$ usando um deslocamento horizontal.

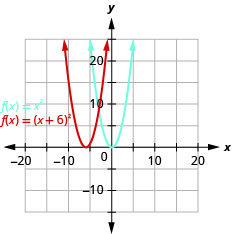
Responda: $Esta figura mostra 2 parábolas de abertura ascendente no plano de coordenadas x y. A curva direita é o gráfico de f de x igual a x ao quadrado que tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A curva esquerda foi movida para as 6 unidades esquerdas.$
Figura 9.7.22

Agora que sabemos o efeito das constantes$h$ e$k$, representaremos graficamente uma função quadrática da forma$f(x)=(x-h)^{2}+k$ desenhando primeiro a parábola básica e depois fazendo um deslocamento horizontal seguido por um deslocamento vertical. Poderíamos fazer o deslocamento vertical seguido pelo deslocamento horizontal, mas a maioria dos estudantes prefere o deslocamento horizontal seguido pelo vertical.

Exemplo$\PageIndex{5}$

Gráfico$f(x)=(x+1)^{2}-2$ usando transformações.

Solução:

Essa função envolverá duas transformações e precisamos de um plano.

Primeiro, vamos identificar as constantes$h, k$.

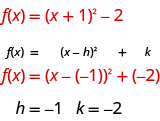
F de x é igual à quantidade x pelúcia 1 quadrado menos 2 é dado na linha superior com f de x igual à quantidade x menos h ao quadrado menos k na segunda linha. A equação dada foi alterada para f de x igual à quantidade de x menos menos 1 quadrado de pelúcia negativo 2 na terceira linha. A linha final diz que h é igual a menos 1 e k é igual a menos 2. — Figura 9.7.23

A$h$ constante nos dá uma mudança horizontal e a nos$k$ dá uma mudança vertical.

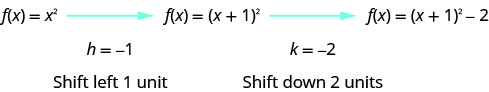
F de x igual a x ao quadrado é dado com uma seta saindo dele apontando para f de x igual à quantidade x mais 1 ao quadrado com uma seta saindo dele apontando para f de x é igual à quantidade x mais 1 quadrado menos 2. As próximas linhas dizem que h é igual a menos 1, o que significa deslocamento para a esquerda 1 unidade e k é igual a menos 2, o que significa deslocamento para baixo 2 unidades. — Figura 9.7.24

Primeiro, desenhamos o gráfico de$f(x)=x^{2}$ na grade.

A figura diz na primeira linha que o gráfico de f de x é igual à quantidade x mais 1 ao quadrado é o mesmo que o gráfico de f de x é igual a x ao quadrado, mas deslocado para a esquerda em 1 unidade. A segunda linha afirma que o gráfico de f de x é igual à quantidade x mais 1 ao quadrado menos 2 é o mesmo que o gráfico de f de x é igual à quantidade x mais 1 ao quadrado, mas deslocado para baixo 2 unidades. — Figura 9.7.25

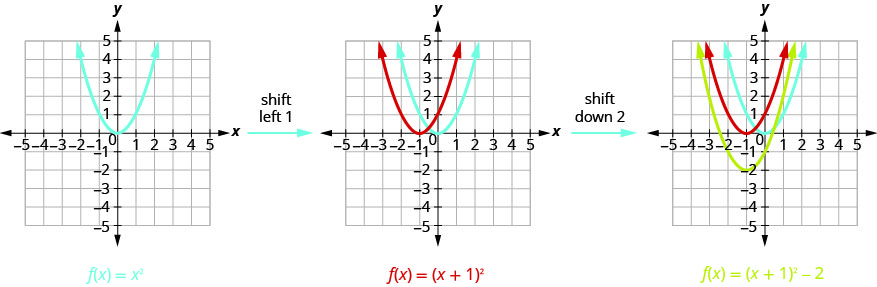
O primeiro gráfico mostra 1 parábola de abertura ascendente no plano de coordenadas x y. É o gráfico de f de x igual a x ao quadrado que tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). Ao deslocar esse gráfico de f de x igual a x quadrado à esquerda 1, passamos para o próximo gráfico, que mostra que o f original de x é igual a x ao quadrado e, em seguida, outra curva movida para a esquerda uma unidade para produzir f de x igual à quantidade de x mais 1 ao quadrado. Ao mover f de x igual à quantidade de x mais 1 ao quadrado abaixo de 1, passamos para o gráfico final, que mostra que o f original de x é igual a x ao quadrado e o f de x é igual à quantidade de x mais 1, então outra curva movida para baixo 1 para produzir f de x igual à quantidade de x mais 1 quadrado menos 2. — Figura 9.7.26

Exercício$\PageIndex{9}$

Gráfico$f(x)=(x+2)^{2}-3$ usando transformações.

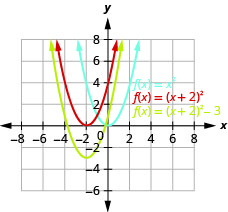
Responda: $Esta figura mostra 3 parábolas de abertura ascendente no plano de coordenadas x y. Um é o gráfico de f de x igual a x ao quadrado e tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). Em seguida, a função original é movida 2 unidades para a esquerda para produzir f de x igual à quantidade de x mais 2 ao quadrado. A curva final é produzida descendo 3 unidades para produzir f de x igual à quantidade de x mais 2 ao quadrado menos 3.$
Figura 9.7.27

Exercício$\PageIndex{10}$

Gráfico$f(x)=(x-3)^{2}+1$ usando transformações.

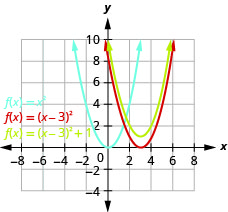
Responda: $Esta figura mostra 3 parábolas de abertura ascendente no plano de coordenadas x y. Um é o gráfico de f de x igual a x ao quadrado e tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). Em seguida, a função original é movida 3 unidades para a direita para produzir f de x igual à quantidade de x menos 3 ao quadrado. A curva final é produzida subindo 1 unidade para produzir f de x igual à quantidade de x menos 3 ao quadrado mais 1.$
Figura 9.7.28

Representar graficamente funções quadráticas do formulário$f(x)=ax^{2}$

Até agora, representamos graficamente a função quadrática$f(x)=x^{2}$ e,$k$ em seguida, vimos o efeito de incluir uma constante$h$ ou na equação no gráfico resultante da nova função. Agora vamos explorar o efeito do coeficiente$a$ no gráfico resultante da nova função$f(x)=ax^{2}$.

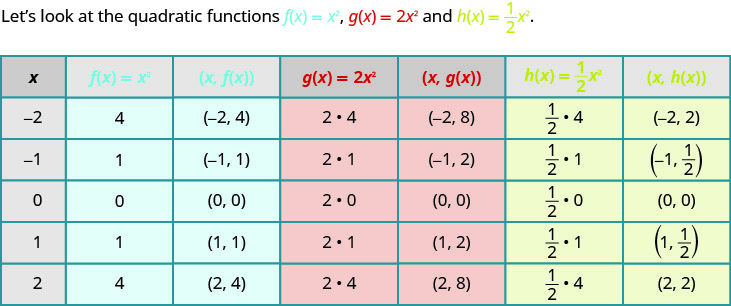
Se representarmos graficamente essas funções, podemos ver o efeito da constante$a$, supondo$a>0$.

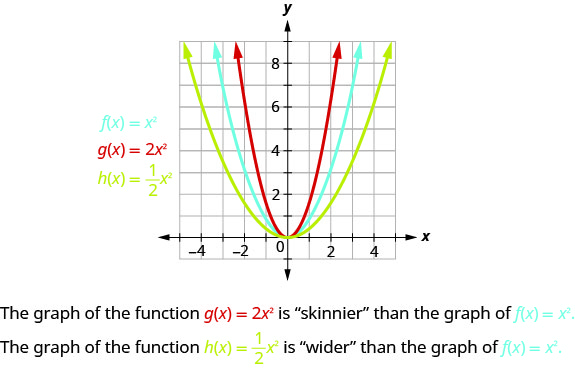
Esta figura mostra 3 parábolas de abertura ascendente no plano de coordenadas x y. Um é o gráfico de f de x igual a x ao quadrado e tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A curva mais fina de g de x igual a 2 vezes x quadrado tem um vértice em (0,0) e outros pontos de (menos 1, meio) e (1, meio). A curva mais larga, h de x igual a meio x ao quadrado, tem um vértice em (0,0) e outros pontos de (menos 2, 2) e (2,2). — Figura 9.7.30

Para representar graficamente uma função com constante,$a$ é mais fácil escolher alguns pontos$f(x)=x^{2}$ e multiplicar os$y$ valores -por$a$.

Gráfico de uma função quadrática da forma$f(x)=ax^{2}$

O coeficiente$a$ na função$f(x)=ax^{2}$ afeta o gráfico de$f(x)=x^{2}$ esticando-o ou comprimindo-o.

Se$0<|a|<1$, o gráfico de$f(x)=ax^{2}$ será “mais largo” do que o gráfico de$f(x)=x^{2}$.
Se$|a|>1$, o gráfico de$f(x)=ax^{2}$ será “mais fino” do que o gráfico de$f(x)=x^{2}$.

Exemplo$\PageIndex{6}$

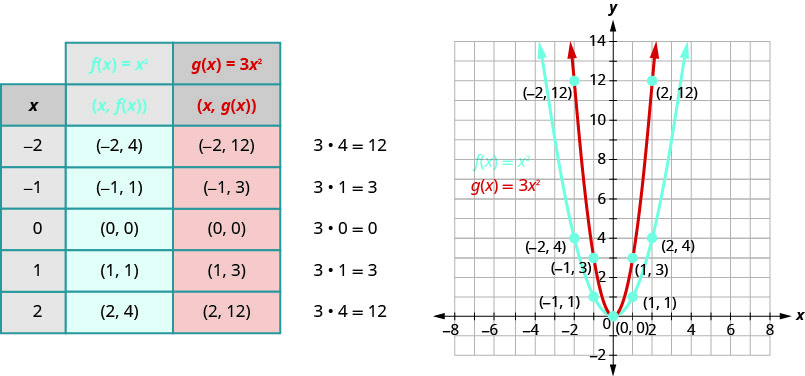
Gráfico$f(x)=3x^{2}$.

Solução:

Vamos representar graficamente as funções$f(x)=x^{2}$ e$g(x)=3x^{2}$ na mesma grade. Escolheremos alguns pontos$f(x)=x^{2}$ e, em seguida, multiplicaremos$y$ os valores -por$3$ para obter os pontos$g(x)=3x^{2}$.

A tabela mostra o efeito das constantes na função básica de x ao quadrado. A tabela tem 3 colunas rotuladas x, f de x é igual a x ao quadrado com o par ordenado (x, f de x) e g de x é igual a 3 vezes x ao quadrado com o par ordenado (x, g de x). Na coluna x, os valores fornecidos são menos 2, menos 1, 0, 1 e 2. No f de x igual a x ao quadrado com o par ordenado (x, f de x), os pares ordenados (menos 2, 4), (menos 1, 1), (0, 0), (1, 1) e (2, 4) são fornecidos. O g de x é igual a 3 vezes x ao quadrado com o par ordenado (x, g de x) a coluna tem os pares ordenados de (menos 2, 12) porque 3 vezes 4 é igual a 12, (menos 1, 3) porque 3 vezes 1 é igual a 3, (0, 0) porque 3 vezes 0 é igual a 0, (1, 3) porque 3 vezes 1 é igual a 3 e (2,12) porque 3 vezes 0 é igual a 0, (1, 3) porque 3 vezes 1 é igual a 3, e (2,12) porque 3 vezes 0 é igual a 0, (1, 3) porque 3 vezes 1 é igual a 3 e vezes 4 é igual a 12. O gráfico ao lado da tabela mostra duas parábolas de abertura ascendente no plano da coordenada x y. Um é o gráfico de f de x igual a x ao quadrado e tem um vértice de (0, 0). Outros pontos dados na curva estão localizados em (menos 2, 4) (menos 1, 1), (1, 1) e (2,4). A curva mais fina de g de x igual a 3 vezes x ao quadrado tem um vértice em (0,0) e outros pontos dados de (menos 2, 12), (menos 1, 3), (1, 3) e (2,12). — Figura 9.7.31

Exercício$\PageIndex{11}$

Gráfico$f(x)=-3x^{2}$.

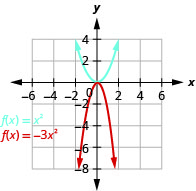
Responda: $O gráfico mostra a parábola de abertura ascendente no plano de coordenadas x y de f de x igual a x ao quadrado que tem um vértice de (0, 0). Outros pontos dados na curva estão localizados em (menos 2, 4) (menos 1, 1), (1, 1) e (2,4). Também é mostrada uma parábola de abertura descendente de f de x igual a menos 3 vezes x ao quadrado. Tem um vértice de (0,0) com outros pontos em (menos 1, menos 3) e (1, menos 3)$
Figura 9.7.32

Exercício$\PageIndex{12}$

Gráfico$f(x)=2x^{2}$.

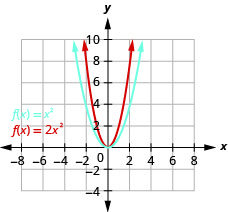
Responda: $Esta figura mostra 2 parábolas de abertura ascendente no plano de coordenadas x y. Um é o gráfico de f de x igual a x ao quadrado e tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A curva mais fina de f de x igual a 2 vezes x quadrado tem um vértice em (0,0) e outros pontos de (menos 1, meio) e (1, meio).$
Figura 9.7.33

Representar graficamente funções quadráticas usando transformações

Aprendemos como as constantes$a, h$ e$k$ nas funções$f(x)=ax^{2}$ afetam seus gráficos.$f(x)=x^{2}+k, f(x)=(x−h)^{2}$ Agora podemos juntar isso e representar graficamente funções$f(x)=ax^{2}+bx+c$ quadráticas colocando-as primeiro no formulário$f(x)=a(x−h)^{2}+k$ completando o quadrado. Essa forma às vezes é conhecida como forma de vértice ou forma padrão.

Devemos ter o cuidado de somar e subtrair o número no MESMO lado da função para completar o quadrado. Não podemos somar o número nos dois lados, como fizemos quando completamos o quadrado com equações quadráticas.

Esta figura mostra a diferença ao completar o quadrado com uma equação quadrática e uma função quadrática. Para a equação quadrática, comece com x ao quadrado mais 8 vezes x mais 6 é igual a zero. Subtraia 6 de ambos os lados para obter x ao quadrado mais 8 vezes x igual a menos 6, deixando espaço para completar o quadrado. Em seguida, complete o quadrado adicionando 16 em ambos os lados para obter x pelúcia quadrada 8 vezes x pelúcia 16 é igual a menos 6 pelúcia 16. Fator para obter a quantidade x mais 4 ao quadrado é igual a 10. Para a função quadrática, comece com f de x igual a x ao quadrado mais 8 vezes x mais 6. A segunda linha mostra como deixar espaço entre o 8 vezes x e o 6 para completar o quadrado. Complete o quadrado adicionando 16 e subtraindo 16 do mesmo lado para obter f de x igual a x ao quadrado mais 8 vezes x pelúcia 16 mais 6 menos 16. O fator para obter f de x é igual à quantidade de x pelúcia 4 ao quadrado menos 10. — Figura 9.7.34

Quando completamos o quadrado em uma função com um coeficiente de$x^{2}$ que não é um, temos que fatorar esse coeficiente apenas a partir dos$x$ termos -. Não consideramos isso a partir do termo constante. Muitas vezes, é útil mover o termo constante um pouco para a direita para facilitar o foco apenas nos$x$ termos.

Depois de obtermos a constante que queremos completar o quadrado, devemos nos lembrar de multiplicá-la por esse coeficiente antes de subtraí-la.

Exemplo$\PageIndex{7}$

Reescreva$f(x)=−3x^{2}−6x−1$ no$f(x)=a(x−h)^{2}+k$ formulário preenchendo o quadrado.

Solução:

Tabela 9.7.3
	$.$
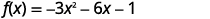Separe os$x$ termos da constante.	$.$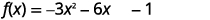
Fator o coeficiente de$x^{2}, -3$.	$.$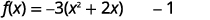
Prepare-se para completar o quadrado.	$.$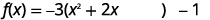
Pegue a metade$2$ e, em seguida, quadre-a para completar o quadrado$(\frac{1}{2}\cdot 2)^{2}=1$
A constante$1$ completa o quadrado entre parênteses, mas os parênteses são multiplicados por$-3$. Então, estamos realmente adicionando$-3$. Devemos então adicionar$3$ para não alterar o valor da função.	$.$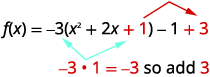
Reescreva o trinômio como um quadrado e subtraia as constantes.	$.$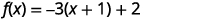
A função agora está no$f(x)=a(x-h)^{2}+k$ formulário.	$.$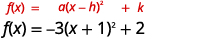

Exercício$\PageIndex{13}$

Reescreva$f(x)=−4x^{2}−8x+1$ no$f(x)=a(x−h)^{2}+k$ formulário preenchendo o quadrado.

Responda: $f(x)=-4(x+1)^{2}+5$

Exercício$\PageIndex{14}$

Reescreva$f(x)=2x^{2}−8x+3$ no$f(x)=a(x−h)^{2}+k$ formulário preenchendo o quadrado.

Responda: $f(x)=2(x-2)^{2}-5$

Depois de colocar a função no$f(x)=(x−h)^{2}+k$ formulário, podemos usar as transformações como fizemos nos últimos problemas. O próximo exemplo nos mostrará como fazer isso.

Exemplo$\PageIndex{8}$

Faça gráficos$f(x)=x^{2}+6x+5$ usando transformações.

Solução:

Etapa 1: reescreva a função na forma de$f(x)=a(x-h)^{2}+k$ vértice completando o quadrado.

Tabela 9.7.4
	$.$
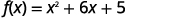Separe os$x$ termos da constante.	$.$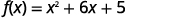
Pegue a metade$6$ e, em seguida, enquadre-a para completar o quadrado. $(\frac{1}{2}\cdot 6)^{2}=9$
Nós dois adicionamos$9$ e subtraímos$9$ para não alterar o valor da função.	$.$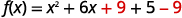
Reescreva o trinômio como um quadrado e subtraia as constantes.	$.$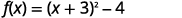
A função agora está no$f(x)=(x-h)^{2}+k$ formulário.	$.$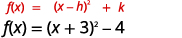

Etapa 2: Faça um gráfico da função usando transformações.

Observando os$h, k$ valores, vemos que o gráfico pegará o gráfico$f(x)=x^{2}$ e o mudará para as$3$ unidades da esquerda e para baixo$4$.

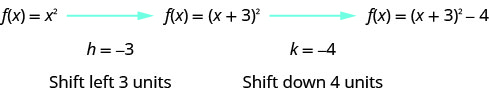
F de x igual a x ao quadrado é dado com uma seta saindo dele apontando para f de x igual à quantidade x mais 3 ao quadrado com uma seta saindo dele apontando para f de x é igual à quantidade x mais 3 ao quadrado menos 4. As próximas linhas dizem que h é igual a menos 3, o que significa deslocamento para a esquerda (3 unidades) e k é igual a menos 4, o que significa deslocamento para baixo (4 unidades). — Figura 9.7.47

Primeiro, desenhamos o gráfico de$f(x)=x^{2}$ na grade.

Para representar graficamente f de x igual à quantidade x mais 3 ao quadrado, desloque o gráfico de f de x é igual a x quadrados para a esquerda 3 unidades. Para representar graficamente f de x igual à quantidade x mais 3 ao quadrado menos 4, mude o gráfico para a quantidade x mais 3 ao quadrado para baixo 4 unidades. — Figura 9.7.48

Exercício$\PageIndex{15}$

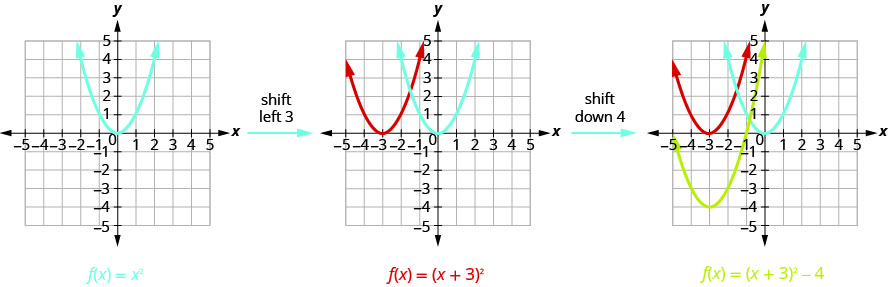
Faça gráficos$f(x)=x^{2}+2x-3$ usando transformações.

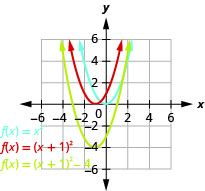
Responda: $Esta figura mostra 3 parábolas de abertura ascendente no plano de coordenadas x y. Um é o gráfico de f de x igual a x ao quadrado e tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A curva à esquerda foi movida 1 unidade para a esquerda para produzir f de x igual à quantidade de x mais 1 quadrado. O terceiro gráfico foi movido para baixo 4 unidades para produzir f de x igual à quantidade de x mais 1 quadrado menos 4.$
Figura 9.7.50

Exercício$\PageIndex{16}$

Faça gráficos$f(x)=x^{2}-8x+12$ usando transformações.

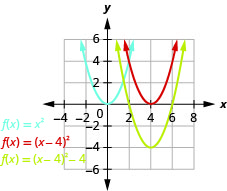
Responda: $Esta figura mostra 3 parábolas de abertura ascendente no plano de coordenadas x y. Um é o gráfico de f de x igual a x ao quadrado e tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A curva para a direita foi movida 4 unidades para a direita para produzir f de x igual à quantidade de x menos 4 ao quadrado. O terceiro gráfico foi movido para baixo 4 unidades para produzir f de x igual à quantidade de x menos 4 ao quadrado menos 4.$
Figura 9.7.51

Listamos as etapas para criar um gráfico de uma função quadrática usando transformações aqui.

Representar graficamente uma função quadrática usando transformações

Reescreva a função na$f(x)=a(x-h)^{2}+k$ forma completando o quadrado.
Faça um gráfico da função usando transformações.

Exemplo$\PageIndex{9}$

Faça gráficos$f(x)=-2x^{2}-4x+2$ usando transformações.

Solução:

Etapa 1: reescreva a função na forma de$f(x)=a(x-h)^{2}+k$ vértice completando o quadrado.

Tabela 9.7.5
	$.$
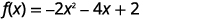Separe os$x$ termos da constante.	$.$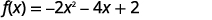
Precisamos que o coeficiente$x^{2}$ de seja um. Nós consideramos a$-2$ partir dos$x$ termos.	$.$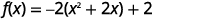
Pegue a metade$2$ e, em seguida, enquadre-a para completar o quadrado. $(\frac{1}{2}\cdot 2)^{2}=1$
Nós adicionamos$1$ para completar o quadrado entre parênteses, mas os parênteses são multiplicados por$-2$. Então, estamos realmente adicionando$-2$. Para não alterar o valor da função, adicionamos$2$.	$.$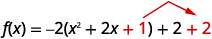
Reescreva o trinômio como um quadrado e subtraia as constantes.	$.$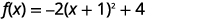
A função agora está no$f(x)=a(x-h)^{2}+k$ formulário.	$.$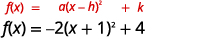

Etapa 2: Faça um gráfico da função usando transformações.

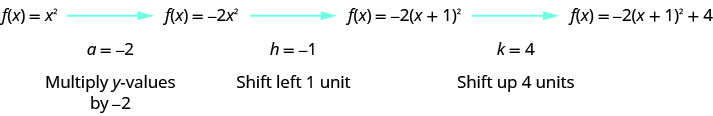
F de x igual a x ao quadrado é dado com uma seta saindo dele apontando para f de x igual a menos 2 vezes x ao quadrado com uma seta saindo dele apontando para f de x igual a menos 2 vezes a quantidade x mais 1 ao quadrado. Uma seta vem dela para apontar para f de x igual a menos 2 vezes a quantidade x mais 1 ao quadrado mais 4. A próxima linha diz que a é igual a menos 2, o que significa multiplicar os valores de y por menos 2, então h é igual a menos 1, o que significa deslocamento para a esquerda 1 unidade e k é igual a 4, o que significa deslocamento para cima 4 unidades. — Figura 9.7.58

Primeiro, desenhamos o gráfico de$f(x)=x^{2}$ na grade.

Para representar graficamente f de x igual a menos 2 vezes x ao quadrado, multiplique os valores de y na parábola de f de x igual a x ao quadrado por menos 2. Para representar graficamente f de x igual a menos 2 vezes a quantidade x mais 1 ao quadrado, desloque o gráfico de f de x igual a menos 2 vezes x ao quadrado para a esquerda 1 unidade. Para representar graficamente f de x igual a menos 2 vezes a quantidade x mais 1 ao quadrado mais 4, mude o gráfico de f de x igual a menos 2 vezes a quantidade x mais 1 ao quadrado até 4 unidades. — Figura 9.7.59

Exercício$\PageIndex{17}$

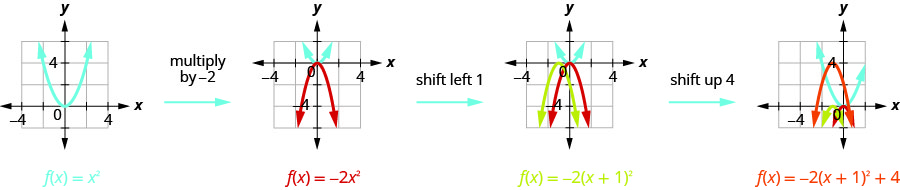
Faça gráficos$f(x)=-3x^{2}+12x-4$ usando transformações.

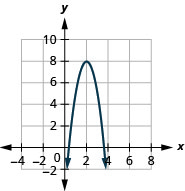
Responda: $Esta figura mostra uma parábola de abertura descendente no plano de coordenadas x y com um vértice de (2,8) e outros pontos de (1,5) e (3,5).$
Figura 9.7.61

Exercício$\PageIndex{18}$

Faça gráficos$f(x)=−2x^{2}+12x−9$ usando transformações.

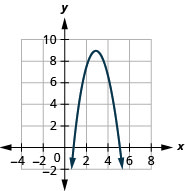
Responda: $Esta figura mostra uma parábola de abertura descendente no plano de coordenadas x y com um vértice de (3, 9) e outros pontos de (1, 1) e (5, 1).$
Figura 9.7.62

Agora que concluímos o quadrado para colocar uma função quadrática em$f(x)=a(x−h)^{2}+k$ forma, também podemos usar essa técnica para representar graficamente a função usando suas propriedades, como na seção anterior.

Se olharmos para os últimos exemplos, veremos que o vértice está relacionado às constantes$h$$k$ e.

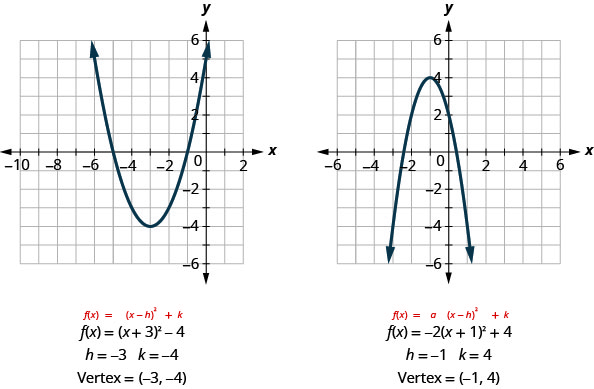
O primeiro gráfico mostra uma parábola de abertura ascendente no plano de coordenadas x y com um vértice de (menos 3, menos 4) com outros pontos de (0, menos 5) e (0, menos 1). Abaixo do gráfico, ele mostra a forma padrão de uma parábola, f de x é igual à quantidade x menos h ao quadrado mais k, com a equação da parábola f de x igual à quantidade de x mais 3 ao quadrado menos 4 onde h é igual a menos 3 e k é igual a menos 4. O segundo gráfico mostra uma parábola de abertura descendente no plano de coordenadas x y com um vértice de (menos 1, 4) e outros pontos de (0,2) e (menos 2,2). Abaixo do gráfico, ele mostra a forma padrão de uma parábola, f de x é igual a uma vez a quantidade x menos h ao quadrado mais k, com a equação da parábola f de x igual a menos 2 vezes a quantidade de x mais 1 quadrado mais 4 onde h é igual a menos 1 e k é igual a 4. — Figura 9.7.63

Em cada caso, o vértice é$(h,k)$. Além disso, o eixo de simetria é a linha$x=h$.

Reescrevemos nossas etapas para representar graficamente uma função quadrática usando propriedades para quando a função está em$f(x)=a(x−h)^{2}+k$ forma.

Representar graficamente uma função quadrática no formulário$f(x)=a(x-h)^{2}+k$ usando propriedades

Reescreva o$f(x)=a(x-h)^{2}+k$ formulário da função.
Determine se a parábola se abre para cima ou para baixo$a<0$.$a>0$
Encontre o eixo de simetria,$x=h$.
Encontre o vértice,$(h,k$.
Encontre o$y$ intercepto -. Encontre o ponto simétrico ao$y$ intercepto -no eixo de simetria.
Encontre as$x$ interceptações -.
Faça um gráfico da parábola.

Exemplo$\PageIndex{10}$

Reescrever$f(x)=2 x^{2}+4 x+5$ no$f(x)=a(x-h)^{2}+k$ formulário
Faça um gráfico da função usando propriedades

Solução:

Tabela 9.7.6
Reescreva a função na$f(x)=a(x-h)^{2}+k$ forma completando o quadrado.	$f(x)=2 x^{2}+4 x+5$
	$f(x)=2\left(x^{2}+2 x\right)+5$
	$f(x)=2\left(x^{2}+2 x+1\right)+5-2$
	$f(x)=2(x+1)^{2}+3$
Identifique as constantes$a, h, k$.	$a=2 h=-1 k=3$
Desde então$a=2$, a parábola se abre para cima.	$.$
O eixo de simetria é$x=h$.	O eixo de simetria é$x=-1$.
O vértice é$(h,k)$.	O vértice é$(-1,3)$.
Encontre o$y$ -intercept encontrando$f(0)$.	$f(0)=2 \cdot 0^{2}+4 \cdot 0+5$
	$f(0)=5$
	$y$-interceptar$(0,5)$
Encontre o ponto simétrico ao$(0,5)$ outro lado do eixo de simetria.	$(-2,5)$
Encontre as$x$ interceptações -.	O discriminante é negativo, então não há$x$ interceptações. Faça um gráfico da parábola.
	$.$

Exercício$\PageIndex{19}$

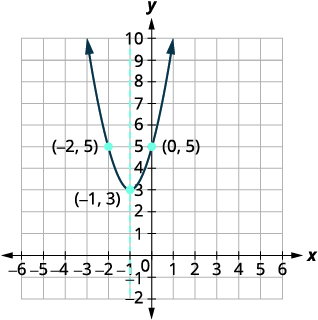Reescrever$f(x)=3 x^{2}-6 x+5$ no$f(x)=a(x-h)^{2}+k$ formulário
Faça um gráfico da função usando propriedades

Responda

$f(x)=3(x-1)^{2}+2$
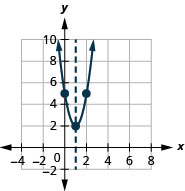
$O gráfico mostrado é uma parábola voltada para cima com vértice (1, 2) e intercepto y (0, 5). O eixo de simetria é mostrado, x é igual a 1.$
Figura 9.7.66

Exercício$\PageIndex{20}$

Reescrever$f(x)=-2 x^{2}+8 x-7$ no$f(x)=a(x-h)^{2}+k$ formulário
Faça um gráfico da função usando propriedades

Responda

$f(x)=-2(x-2)^{2}+1$
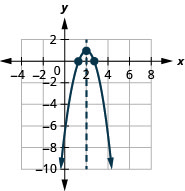
$O gráfico mostrado é uma parábola voltada para baixo com vértice (2, 1) e interceptos x (1, 0) e (3, 0). O eixo de simetria é mostrado, x é igual a 2.$
Figura 9.7.67

Encontre uma função quadrática a partir de seu gráfico

Até agora, começamos com uma função e depois encontramos seu gráfico.

Agora vamos reverter o processo. Começando com o gráfico, encontraremos a função.

Exemplo$\PageIndex{11}$

Determine a função quadrática cujo gráfico é mostrado.

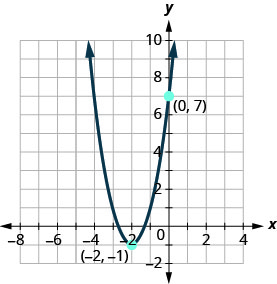
O gráfico mostrado é uma parábola voltada para cima com vértice (menos 2, menos 1) e intercepto y (0, 7). — Figura 9.7.68

Solução:

Como é quadrático, começamos com o$f(x)=a(x−h)^{2}+k$ formulário.

O vértice$(h,k)$,, é$(−2,−1)$ assim$h=−2$$k=−1$ e.

$f(x)=a(x-(-2))^{2}-1$

Para encontrar$a$, usamos o$y$ -intercept,$(0,7)$.

Então$f(0)=7$.

$7=a(0+2)^{2}-1$

Resolver para$a$.

$\begin{array}{l}{7=4 a-1} \\ {8=4 a} \\ {2=a}\end{array}$

Escreva a função.

$f(x)=a(x-h)^{2}+k$

$h=-2, k=-1$Substitua$a=2$ e.

$f(x)=2(x+2)^{2}-1$

Exercício$\PageIndex{21}$

Escreva a função quadrática na$f(x)=a(x−h)^{2}+k$ forma cujo gráfico é mostrado.

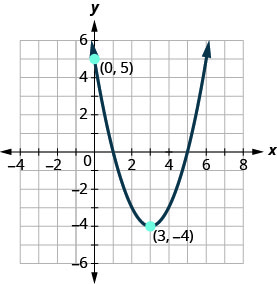
O gráfico mostrado é uma parábola voltada para cima com vértice (3, menos 4) e intercepto y (0, 5). — Figura 9.7.69

Responda: $f(x)=(x-3)^{2}-4$

Exercício$\PageIndex{22}$

Determine a função quadrática cujo gráfico é mostrado.

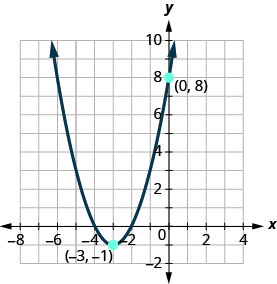
O gráfico mostrado é uma parábola voltada para cima com vértice (menos 3, menos 1) e intercepto y (0, 8). — Figura 9.7.70

Responda: $f(x)=(x+3)^{2}-1$

Acesse esses recursos on-line para obter instruções e práticas adicionais com a representação gráfica de funções quadráticas usando transformações.

Conceitos-chave

Representar graficamente uma função quadrática do formulário$f(x)=x^{2}+k$ usando um deslocamento vertical
- O gráfico de$f(x)=x^{2}+k$ desloca o gráfico das$k$ unidades$f(x)=x^{2}$ verticais.
  - Se$k>0$, desloque a parábola verticalmente para cima$k$ das unidades.
  - Se$k<0$, desloque a parábola verticalmente para baixo em$|k|$ unidades.
Representar graficamente uma função quadrática do formulário$f(x)=(x−h)^{2}$ usando um deslocamento horizontal
- O gráfico de$f(x)=(x−h)^{2}$ desloca o gráfico das$h$ unidades$f(x)=x^{2}$ horizontais.
  - Se$h>0$, desloque a parábola horizontalmente para a$h$ esquerda.
  - Se$h<0$, desloque a parábola horizontalmente para a$|h|$ direita.
Gráfico de uma função quadrática da forma$f(x)=ax^{2}$
- O coeficiente$a$ na função$f(x)=ax^{2}$ afeta o gráfico de$f(x)=x^{2}$ esticando-o ou comprimindo-o.
  Se$0<|a|<1$, então o gráfico de$f(x)=ax^{2}$ será “mais largo” do que o gráfico de$f(x)=x^{2}$.
  Se$|a|>1$, então o gráfico de$f(x)=ax^{2}$ será “mais fino” do que o gráfico de$f(x)=x^{2}$.
Como representar graficamente uma função quadrática usando transformações
1. Reescreva a função na$f(x)=a(x−h)^{2}+k$ forma completando o quadrado.
2. Faça um gráfico da função usando transformações.
Representar graficamente uma função quadrática na forma de vértice$f(x)=a(x−h)^{2}+k$ usando propriedades
1. Reescreva a função no$f(x)=a(x−h)^{2}+k$ formulário.
2. Determine se a parábola se abre para cima ou para baixo$a<0$.$a>0$
3. Encontre o eixo de simetria,$x=h$.
4. Encontre o vértice,$(h,k)$.
5. Encontre o$y$ intercepto -. Encontre o ponto simétrico ao$y$ intercepto -no eixo de simetria.
6. Encontre os$x$ -intercepts, se possível.
7. Faça um gráfico da parábola.

Reescreva a função na\(f(x)=a(x-h)^{2}+k\) forma completando o quadrado.	\(f(x)=2 x^{2}+4 x+5\)
	\(f(x)=2\left(x^{2}+2 x\right)+5\)
	\(f(x)=2\left(x^{2}+2 x+1\right)+5-2\)
	\(f(x)=2(x+1)^{2}+3\)
Identifique as constantes\(a, h, k\).	\(a=2 h=-1 k=3\)
Desde então\(a=2\), a parábola se abre para cima.	$.$
O eixo de simetria é\(x=h\).	O eixo de simetria é\(x=-1\).
O vértice é\((h,k)\).	O vértice é\((-1,3)\).
Encontre o\(y\) -intercept encontrando\(f(0)\).	\(f(0)=2 \cdot 0^{2}+4 \cdot 0+5\)
	\(f(0)=5\)
	\(y\)-interceptar\((0,5)\)
Encontre o ponto simétrico ao\((0,5)\) outro lado do eixo de simetria.	\((-2,5)\)
Encontre as\(x\) interceptações -.	O discriminante é negativo, então não há\(x\) interceptações. Faça um gráfico da parábola.
	$.$

Exemplo\(\PageIndex{1}\)

Exercício\(\PageIndex{1}\)

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{2}\)

Exercício\(\PageIndex{3}\)

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{3}\)

Exercício\(\PageIndex{5}\)

Exercício\(\PageIndex{6}\)

Exemplo\(\PageIndex{4}\)

Exercício\(\PageIndex{7}\)

Exercício\(\PageIndex{8}\)

Exemplo\(\PageIndex{5}\)

Exercício\(\PageIndex{9}\)

Exercício\(\PageIndex{10}\)

Exemplo\(\PageIndex{6}\)

Exercício\(\PageIndex{11}\)

Exercício\(\PageIndex{12}\)

Exemplo\(\PageIndex{7}\)

Exercício\(\PageIndex{13}\)

Exercício\(\PageIndex{14}\)

Exemplo\(\PageIndex{8}\)

Exercício\(\PageIndex{15}\)

Exercício\(\PageIndex{16}\)

Exemplo\(\PageIndex{9}\)

Exercício\(\PageIndex{17}\)

Exercício\(\PageIndex{18}\)

Exemplo\(\PageIndex{10}\)

Exercício\(\PageIndex{19}\)

Exercício\(\PageIndex{20}\)

Exemplo\(\PageIndex{11}\)

Exercício\(\PageIndex{21}\)

Exercício\(\PageIndex{22}\)

Primeiro, desenhamos o gráfico de\(f(x)=x^{2}\) na grade.	$Esta figura mostra uma parábola de abertura ascendente no plano de coordenadas x y com um vértice de (0, 0) com outros pontos na curva localizados em (menos 1, 1) e (1, 1). É o gráfico de f de x igual a x ao quadrado.$
Determinar\(k\).	$.$
	$.$
Desloque o gráfico\(f(x)=x^{2}\) para baixo\(3\).	$Esta figura mostra 2 parábolas de abertura ascendente no plano de coordenadas x y. A curva superior é o gráfico de f de x igual a x ao quadrado que tem um vértice de (0, 0). Outros pontos na curva estão localizados em (menos 1, 1) e (1, 1). A curva inferior foi movida para baixo em 3 unidades.$

Primeiro, desenhamos o gráfico de\(f(x)=x^{2}\) na grade.	$.$
Determinar\(h\).	$.$
	$.$
Desloque o gráfico\(f(x)=x^{2}\) para as\(6\) unidades certas.	$.$

	$.$
Separe os\(x\) termos da constante.	$.$
Fator o coeficiente de\(x^{2}, -3\).	$.$
Prepare-se para completar o quadrado.	$.$
Pegue a metade\(2\) e, em seguida, quadre-a para completar o quadrado\((\frac{1}{2}\cdot 2)^{2}=1\)
A constante\(1\) completa o quadrado entre parênteses, mas os parênteses são multiplicados por\(-3\). Então, estamos realmente adicionando\(-3\). Devemos então adicionar\(3\) para não alterar o valor da função.	$.$
Reescreva o trinômio como um quadrado e subtraia as constantes.	$.$
A função agora está no\(f(x)=a(x-h)^{2}+k\) formulário.	$.$

	$.$
Separe os\(x\) termos da constante.	$.$
Pegue a metade\(6\) e, em seguida, enquadre-a para completar o quadrado. \((\frac{1}{2}\cdot 6)^{2}=9\)
Nós dois adicionamos\(9\) e subtraímos\(9\) para não alterar o valor da função.	$.$
Reescreva o trinômio como um quadrado e subtraia as constantes.	$.$
A função agora está no\(f(x)=(x-h)^{2}+k\) formulário.	$.$

	$.$
Separe os\(x\) termos da constante.	$.$
Precisamos que o coeficiente\(x^{2}\) de seja um. Nós consideramos a\(-2\) partir dos\(x\) termos.	$.$
Pegue a metade\(2\) e, em seguida, enquadre-a para completar o quadrado. \((\frac{1}{2}\cdot 2)^{2}=1\)
Nós adicionamos\(1\) para completar o quadrado entre parênteses, mas os parênteses são multiplicados por\(-2\). Então, estamos realmente adicionando\(-2\). Para não alterar o valor da função, adicionamos\(2\).	$.$
Reescreva o trinômio como um quadrado e subtraia as constantes.	$.$
A função agora está no\(f(x)=a(x-h)^{2}+k\) formulário.	$.$

Objetivos de

Representar graficamente funções quadráticas do formulário\(f(x)=x^{2}+k\)

Exemplo\(\PageIndex{1}\)

Exercício\(\PageIndex{1}\)

Exercício\(\PageIndex{2}\)

Representar graficamente uma função quadrática do formulário\(f(x)=x^{2}+k\) usando um deslocamento vertical

Exemplo\(\PageIndex{2}\)

Exercício\(\PageIndex{3}\)

Exercício\(\PageIndex{4}\)

Representar graficamente funções quadráticas do formulário\(f(x)=(x-h)^{2}\)

Exemplo\(\PageIndex{3}\)

Exercício\(\PageIndex{5}\)

Exercício\(\PageIndex{6}\)

Representar graficamente uma função quadrática do formulário\(f(x)=(x-h)^{2}\) usando um deslocamento horizontal

Exemplo\(\PageIndex{4}\)

Exercício\(\PageIndex{7}\)

Exercício\(\PageIndex{8}\)

Exemplo\(\PageIndex{5}\)

Exercício\(\PageIndex{9}\)

Exercício\(\PageIndex{10}\)

Representar graficamente funções quadráticas do formulário\(f(x)=ax^{2}\)

Gráfico de uma função quadrática da forma\(f(x)=ax^{2}\)

Exemplo\(\PageIndex{6}\)

Exercício\(\PageIndex{11}\)

Exercício\(\PageIndex{12}\)

Representar graficamente funções quadráticas usando transformações

Exemplo\(\PageIndex{7}\)

Exercício\(\PageIndex{13}\)

Exercício\(\PageIndex{14}\)

Exemplo\(\PageIndex{8}\)

Exercício\(\PageIndex{15}\)

Exercício\(\PageIndex{16}\)

Representar graficamente uma função quadrática usando transformações

Exemplo\(\PageIndex{9}\)

Exercício\(\PageIndex{17}\)

Exercício\(\PageIndex{18}\)

Representar graficamente uma função quadrática no formulário\(f(x)=a(x-h)^{2}+k\) usando propriedades

Exemplo\(\PageIndex{10}\)

Exercício\(\PageIndex{19}\)

Exercício\(\PageIndex{20}\)

Encontre uma função quadrática a partir de seu gráfico

Exemplo\(\PageIndex{11}\)

Exercício\(\PageIndex{21}\)

Exercício\(\PageIndex{22}\)

Conceitos-chave