9.6: Resolver aplicações de equações quadráticas
- Page ID
- 183553
Ao final desta seção, você poderá:
- Resolva aplicações modeladas por equações quadráticas
Antes de começar, faça este teste de prontidão.
- A soma de dois números ímpares consecutivos é\(−100\). Encontre os números.
Se você perdeu esse problema, revise o Exemplo 2.18. - Resolver:\(\frac{2}{x+1}+\frac{1}{x-1}=\frac{1}{x^{2}-1}\).
Se você perdeu esse problema, consulte o Exemplo 7.35. - Encontre o comprimento da hipotenusa de um triângulo reto com pernas em\(5\) polegadas e\(12\) polegadas.
Se você perdeu esse problema, consulte o Exemplo 2.34.
Resolva aplicações modeladas por equações quadráticas
Resolvemos algumas aplicações que foram modeladas por equações quadráticas anteriormente, quando o único método que tínhamos para resolvê-las era a fatoração. Agora que temos mais métodos para resolver equações quadráticas, daremos outra olhada nas aplicações.
Vamos primeiro resumir os métodos que temos agora para resolver equações quadráticas.
Métodos para resolver equações quadráticas
- Fatorar
- Propriedade de raiz quadrada
- Completando a Praça
- Fórmula quadrática
Ao resolver cada equação, escolha o método mais conveniente para resolver o problema. Como lembrete, copiaremos nossa estratégia usual de solução de problemas aqui para que possamos seguir as etapas.
Use uma estratégia de solução de problemas
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que estamos procurando.
- Diga o que estamos procurando. Escolha uma variável para representar essa quantidade.
- Traduza em uma equação. Pode ser útil reafirmar o problema em uma frase com todas as informações importantes. Em seguida, traduza a frase em inglês em uma equação algébrica.
- Resolva a equação usando técnicas de álgebra.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
Resolvemos aplicações numéricas que envolviam números inteiros pares e ímpares consecutivos, modelando a situação com equações lineares. Lembre-se de que notamos que cada número inteiro par é\(2\) maior do que o número que o precede. Se chamarmos o primeiro\(n\), então o próximo é\(n+2\). O próximo seria\(n+2+2\) ou\(n+4\). Isso também é verdade quando usamos números inteiros ímpares. Um conjunto de números inteiros pares e um conjunto de números inteiros ímpares são mostrados abaixo.
\(\begin{array}{cl}{}&{\text{Consecutive even integers}}\\{}& {64,66,68}\\ {n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer }}\end{array}\)
\(\begin{array}{cl}{}&{\text{Consecutive odd integers}}\\{}& {77,79,81}\\ {n} & {1^{\text { st }} \text { odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer }}\end{array}\)
Algumas aplicações de números inteiros ímpares ou mesmo consecutivos são modeladas por equações quadráticas. A notação acima será útil ao nomear as variáveis.
O produto de dois números inteiros ímpares consecutivos é\(195\). Encontre os números inteiros.
Solução:
Etapa 1: leia o problema
Etapa 2: Identifique o que estamos procurando.
Estamos procurando por dois números inteiros ímpares consecutivos.
Etapa 3: nomeie o que estamos procurando.
Deixe\(n=\) o primeiro número inteiro ímpar.
\(n+2=\)o próximo número inteiro ímpar.
Etapa 4: traduza em uma equação. Indique o problema em uma frase.
“O produto de dois números inteiros ímpares consecutivos é\(195\).” O produto do primeiro inteiro ímpar e do segundo inteiro ímpar é\(195\).
Traduza em uma equação.
\(n(n+2)=195\)
Etapa 5: Resolva a equação. Distribuir.
\(n^{2}+2 n=195\)
Escreva a equação na forma padrão.
\(n^{2}+2 n-195=0\)
Fator.
\((n+15)(n-13)=0\)
Use a propriedade Zero Product.
\(n+15=0 \quad n-13=0\)
Resolva cada equação.
\(n=-15, \quad n=13\)
Existem dois valores\(n\) que são soluções. Isso nos dará dois pares de números inteiros ímpares consecutivos para nossa solução.
\(\begin{array}{cc}{\text { First odd integer } n=13} & {\text { First odd integer } n=-15} \\ {\text { next odd integer } n+2} & {\text { next odd integer } n+2} \\ {13+2} & {-15+2} \\ {15} & {-13}\end{array}\)
Etapa 6: verifique a resposta.
Esses pares funcionam? Eles são números inteiros ímpares consecutivos?
\(\begin{aligned} 13,15 & \text { yes } \\-13,-15 & \text { yes } \end{aligned}\)
É o produto deles\(195\)?
\(\begin{aligned} 13 \cdot 15 &=195 &\text{yes} \\-13(-15) &=195 & \text { yes } \end{aligned}\)
Etapa 7: Responda à pergunta.
Dois números inteiros ímpares consecutivos cujo produto é\(195\)\(13,15\)\(-13,-15\) e.
O produto de dois números inteiros ímpares consecutivos é\(99\). Encontre os números inteiros.
- Resposta
-
Os dois números inteiros ímpares consecutivos cujo produto é\(99\)\(9, 11\),\(−9, −11\) e.
O produto de dois números inteiros pares consecutivos é\(168\). Encontre os números inteiros.
- Resposta
-
Os dois números inteiros pares consecutivos cujo produto é\(128\) são\(12, 14\)\(−12, −14\) e.
Usaremos a fórmula da área de um triângulo para resolver o próximo exemplo.
Área de um triângulo
Para um triângulo com base,\(b\), e altura\(h\),, a área\(A\),, é dada pela fórmula\(A=\frac{1}{2} b h\).
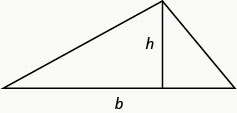
Lembre-se de que, quando resolvemos aplicações geométricas, é útil desenhar a figura.
Um arquiteto está projetando a entrada de um restaurante. Ela quer colocar uma janela triangular acima da porta. Devido às restrições de energia, a janela só pode ter uma área de pés\(120\) quadrados e o arquiteto quer que a base tenha\(4\) pés a mais do que o dobro da altura. Encontre a base e a altura da janela.
Solução:
| Etapa 1: Leia o problema. Faça um desenho. | 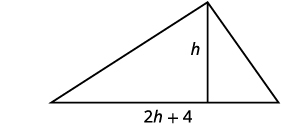 |
| Etapa 2: Identifique o que estamos procurando. | Estamos procurando a base e a altura. |
| Etapa 3: nomeie o que estamos procurando. |
Deixe\(h=\) a altura do triângulo. \(2h+4=\)a base do triângulo. |
|
Etapa 4: traduza em uma equação. Conhecemos a área. Escreva a fórmula para a área de um triângulo. |
\(A=\frac{1}{2} b h\) |
| Etapa 5: Resolva a equação. Substitua os valores. | \(120=\frac{1}{2}(2 h+4) h\) |
| Distribuir. | \(120=h^{2}+2 h\) |
| Esta é uma equação quadrática, reescreva-a na forma padrão. | \(h^{2}+2 h-120=0\) |
| Fator. | \((h-10)(h+12)=0\) |
| Use a propriedade Zero Product. | \(h-10=0 \quad h+12=0\) |
| Simplifique. | \(h=10, \quad \cancel{h=-12}\) |
| Como\(h\) é a altura de uma janela, um valor de não\(h=-12\) faz sentido. | |
| A altura do triângulo\(h=10\). | |
|
A base do triângulo\(2h+4\). \(2 \cdot 10+4\) \(24\) |
|
|
Etapa 6: verifique a resposta. Um triângulo com altura\(10\) e base\(24\) tem área\(120\)? Sim. |
|
| Etapa 7: Responda à pergunta. | A altura da janela triangular é de\(10\) pés e a base é de\(24\) pés. |
Encontre a base e a altura de um triângulo cuja base é quatro polegadas a mais do que seis vezes sua altura e tem uma área de polegadas\(456\) quadradas.
- Resposta
-
A altura do triângulo é em\(12\) polegadas e a base em\(76\) polegadas.
Se um triângulo que tem uma área de pés\(110\) quadrados tem uma base que é dois pés a menos que o dobro da altura, qual é o comprimento de sua base e altura?
- Resposta
-
A altura do triângulo é\(11\) pés e a base é\(20\) pés.
Nos dois exemplos anteriores, o número no radical na Fórmula Quadrática era um quadrado perfeito e, portanto, as soluções eram números racionais. Se obtivermos um número irracional como solução para um problema de aplicação, usaremos uma calculadora para obter um valor aproximado.
Usaremos a fórmula da área de um retângulo para resolver o próximo exemplo.
Área de um retângulo
Para um retângulo com comprimento,\(L\), e largura\(W\),, a área\(A\),, é dada pela fórmula\(A=LW\).
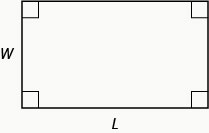
Mike quer colocar pés\(150\) quadrados de grama artificial em seu jardim. Esta é a área máxima de grama artificial permitida por sua associação de proprietários. Ele quer ter uma área retangular de relva com comprimento de um pé a menos do que o\(3\) dobro da largura. Encontre o comprimento e a largura. Arredonde para o décimo de pé mais próximo.
Solução:
| Etapa 1: Leia o problema. Faça um desenho. |  |
| Etapa 2: Identifique o que estamos procurando. | Estamos procurando o comprimento e a largura. |
| Etapa 3: nomeie o que estamos procurando. |
Deixe\(w=\) a largura do retângulo. \(3w-1=\)o comprimento do retângulo |
| Etapa 4: traduza em uma equação. Conhecemos a área. Escreva a fórmula para a área de um retângulo. |  |
| Etapa 5: Resolva a equação. Substitua os valores. | 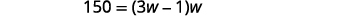 |
| Distribuir. | 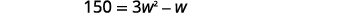 |
|
Essa é uma equação quadrática; reescreva-a na forma padrão. Resolva a equação usando a fórmula quadrática. |
 |
| Identifique os\(a,b,c\) valores. |  |
| Escreva a fórmula quadrática. | 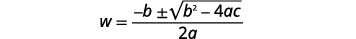 |
| Em seguida, substitua os valores de\(a,b,c\). | 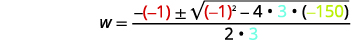 |
| Simplifique. | 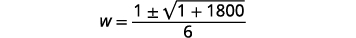
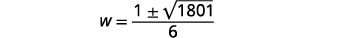
|
| Reescreva para mostrar duas soluções. | 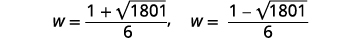 |
|
Aproxime as respostas usando uma calculadora. Eliminamos a solução negativa para a largura. |
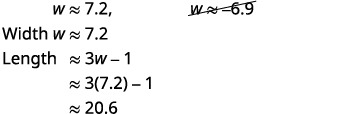 |
| Etapa 6: verifique a resposta. Certifique-se de que as respostas façam sentido. Como as respostas são aproximadas, a área não será exibida exatamente para\(150\). | |
| Etapa 7: Responda à pergunta. | A largura do retângulo é de aproximadamente\(7.2\) pés e o comprimento é de aproximadamente\(20.6\) pés. |
O comprimento de uma horta retangular de um metro\(200\) quadrado é quatro pés a menos que o dobro da largura. Encontre o comprimento e a largura do jardim, até o décimo de pé mais próximo.
- Resposta
-
O comprimento do jardim é de aproximadamente\(18\) pés e a largura de\(11\) pés.
Uma toalha de mesa retangular tem uma área de pés\(80\) quadrados. A largura é\(5\) pés mais curta que o comprimento. Quais são o comprimento e a largura da toalha de mesa até o décimo de pé mais próximo?
- Resposta
-
O comprimento da toalha de mesa é de aproximadamente\(11.8\) pés e a largura de\(6.8\) pés.
O Teorema de Pitágoras fornece a relação entre as pernas e a hipotenusa de um triângulo reto. Usaremos o Teorema de Pitágoras para resolver o próximo exemplo.
Teorema de Pitágoras
Em qualquer triângulo reto, onde\(a\) e\(b\) estão os comprimentos das pernas, e\(c\) é o comprimento da hipotenusa,\(a^{2}+b^{2}=c^{2}\).
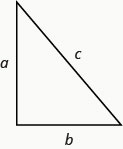
Rene está montando um display de luzes natalinas. Ele quer fazer uma 'árvore' na forma de dois triângulos retos, como mostrado abaixo, e tem cordas de luzes de dois\(10\) pés para usar nas laterais. Ele colocará as luzes no topo de um poste e em duas estacas no chão. Ele quer que a altura do poste seja a mesma que a distância da base do poste até cada estaca. Qual deve ser a altura do poste?
Solução:
| Etapa 1: Leia o problema. Faça um desenho. | 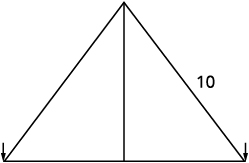 |
| Etapa 2: Identifique o que estamos procurando. | Estamos procurando a altura do poste. |
| Etapa 3: nomeie o que estamos procurando. |
A distância da base do poste até qualquer estaca é igual à altura do poste. Deixe\(x=\) a altura do poste. Cada lado é um triângulo reto. Nós desenhamos uma foto de um deles. 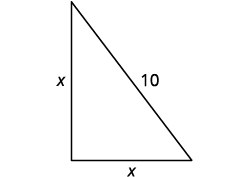
|
|
Etapa 4: traduza em uma equação. Podemos usar o Teorema de Pitágoras para resolver\(x\). |
\(a^{2}+b^{2}=c^{2}\) |
| Etapa 5: Resolva a equação. Substituto. | \(x^{2}+x^{2}=10^{2}\) |
| Simplifique. | \(2 x^{2}=100\) |
| Divida por\(2\) para isolar a variável. | \(\frac{2 x^{2}}{2}=\frac{100}{2}\) |
| Simplifique. | \(x^{2}=50\) |
| Use a propriedade Square Root. | \(x=\pm \sqrt{50}\) |
| Simplifique o radical. | \(x=\pm 5 \sqrt{2}\) |
| Reescreva para mostrar duas soluções. | \(x=5 \sqrt{2}, \quad \cancel{x=-5 \sqrt{2}}\) |
| Se aproximarmos esse número ao décimo mais próximo com uma calculadora, encontraremos\(x≈7.1\). | |
| Etapa 6: verifique a resposta. Verifique por si mesmo no Teorema de Pitágoras. | |
| Etapa 7: Responda à pergunta. | O poste deve ter cerca de um\(7.1\) metro de altura. |
O sol projeta uma sombra de um mastro de bandeira. A altura do mastro da bandeira é três vezes o comprimento de sua sombra. A distância entre a extremidade da sombra e o topo do mastro da bandeira é de\(20\) pés. Encontre o comprimento da sombra e o comprimento do mastro da bandeira. Arredonde para o décimo mais próximo.
- Resposta
-
O comprimento da sombra do mastro da bandeira é de aproximadamente\(6.3\) pés e a altura do mastro é de\(18.9\) pés.
A distância entre os cantos opostos de um campo retangular é quatro a mais do que a largura do campo. O comprimento do campo é o dobro da largura. Encontre a distância entre os cantos opostos. Arredonde para o décimo mais próximo.
- Resposta
-
A distância entre os cantos opostos é de aproximadamente\(7.2\) pés.
A altura de um projétil disparado do solo é modelada por uma equação quadrática. A velocidade inicial,\(v_{0}\), impulsiona o objeto até que a gravidade faça com que o objeto caia novamente.
A altura em pés\(h\),, de um objeto lançado para cima no ar com velocidade inicial,\(v_{0}\), após\(t\) segundos é dada pela fórmula
\(h=-16 t^{2}+v_{0} t\)
Podemos usar essa fórmula para descobrir quantos segundos serão necessários para um fogo de artifício atingir uma altura específica.
Um fogo de artifício é disparado para cima com velocidade inicial\(130\) pés por segundo. Quantos segundos serão necessários para atingir uma altura de\(260\) pés? Arredonde para o décimo de segundo mais próximo.
Solução:
| Etapa 1: Leia o problema. | |
| Etapa 2: Identifique o que estamos procurando. | Estamos procurando o número de segundos, que é o tempo. |
| Etapa 3: nomeie o que estamos procurando. | Deixe\(t=\) o número de segundos. |
| Etapa 4: traduza em uma equação. Use a fórmula. | 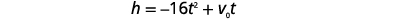 |
| Etapa 5: Resolva a equação. Sabemos que a velocidade\(v_{0}\) é\(130\) pés por segundo. A altura é de\(260\) pés. Substitua os valores. | 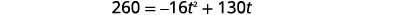 |
| Esta é uma equação quadrática, reescreva-a na forma padrão. Resolva a equação usando a fórmula quadrática. |  |
| Identifique os valores de\(a, b, c\). |  |
| Escreva a fórmula quadrática. | 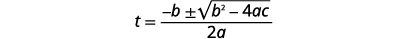 |
| Em seguida, substitua os valores de\(a,b,c\). | 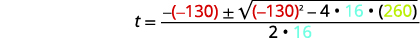 |
| Simplifique. | 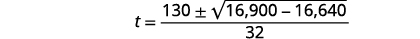
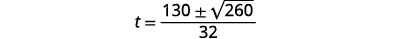
|
| Reescreva para mostrar duas soluções. | 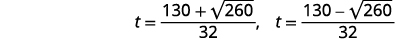 |
| Aproxime a resposta com uma calculadora. |  |
| Etapa 6: verifique a resposta. O cheque é deixado para você. | |
| Etapa 7: Responda à pergunta. | Os fogos de artifício subirão e depois cairão novamente. Conforme o fogo de artifício aumenta, ele alcançará\(260\) pés após aproximadamente\(3.6\) segundos. Ele também passará dessa altura na descida em\(4.6\) segundos. |
Uma flecha é disparada do chão para o ar a uma velocidade inicial de\(108\) pés/s. Use a fórmula\(h=-16 t^{2}+v_{0} t\) para determinar quando a flecha estará a\(180\) pés do chão. Arredonde o décimo mais próximo.
- Resposta
-
A flecha alcançará\(180\) os pés ao subir após\(3\) segundos e novamente descerá após aproximadamente\(3.8\) segundos.
Um homem joga uma bola no ar com uma velocidade de\(96\) pés/s. Use a fórmula\(h=-16 t^{2}+v_{0} t\) para determinar quando a altura da bola será de\(48\) pés. Arredonde para o décimo mais próximo.
- Resposta
-
A bola alcançará\(48\) os pés em seu caminho para cima após aproximadamente um\(.6\) segundo e novamente em sua descida após aproximadamente\(5.4\) segundos.
Resolvemos problemas de movimento uniforme usando a fórmula\(D=rt\) dos capítulos anteriores. Usamos uma tabela como a abaixo para organizar as informações e nos levar à equação.

A fórmula\(D=rt\) pressupõe que nós os conhecemos\(r\)\(t\) e os usamos para encontrar\(D\). Se soubéssemos\(D\) \(r\)e precisássemos encontrar\(t\), resolveríamos a equação\(t\) e obteríamos a fórmula\(t=\frac{D}{r}\).
Alguns problemas de movimento uniforme também são modelados por equações quadráticas.
O professor Smith acabou de voltar de uma conferência que ficava\(2,000\) a quilômetros a leste de sua casa. Seu tempo total no avião para a viagem de ida e volta foi de\(9\) horas. Se o avião estivesse voando a uma taxa de\(450\) milhas por hora, qual era a velocidade da corrente de jato?
Solução:
Esta é uma situação de movimento uniforme. Um diagrama nos ajudará a visualizar a situação.

Preenchemos o gráfico para organizar as informações.
Estamos procurando a velocidade da corrente de jato. Deixe\(r=\) a velocidade do jato fluir.
Quando o avião voa com o vento, o vento aumenta sua velocidade e, portanto, a taxa aumenta\(450 + r\).
Quando o avião voa contra o vento, o vento diminui sua velocidade e a taxa é\(450 − r\).
| Escreva nas tarifas. Escreva à distância. Desde então\(D=r⋅t\), resolvemos \(t\) e obtemos\(t=\frac{D}{r}\). Dividimos a distância pela taxa em cada linha e colocamos a expressão na coluna de tempo. |
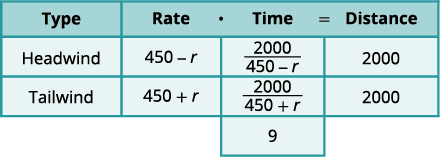 |
| Sabemos que os tempos aumentam\(9\) e, por isso, escrevemos nossa equação. |
\(\frac{2000}{450-r}+\frac{2000}{450+r}=9\) |
| Multiplicamos os dois lados pelo LCD. | \((450-r)(450+r)\left(\frac{2000}{450-r}+\frac{2000}{450+r}\right)=9(450-r)(450+r)\) |
| Simplifique. | \(2000(450+r)+2000(450-r)=9(450-r)(450+r)\) |
| Fator\(2,000\) o. | \(2000(450+r+450-r)=9\left(450^{2}-r^{2}\right)\) |
| Resolver. | \(2000(900)=9\left(450^{2}-r^{2}\right)\) |
| Divida por\(9\). | \(2000(100)=450^{2}-r^{2}\) |
| Simplifique. |
\(\begin{aligned}200000&=202500-r^{2} \\ -2500&=-r^{2}\\ 50&=r\end{aligned}\)\ A velocidade da corrente de jato é\(50\) mph. |
|
Confira: O\(50\) mph é uma velocidade razoável para a corrente de jato? Sim. Se o avião estiver viajando\(450\) mph e o vento estiver em\(50\) mph, vento de cauda \(450+50=500 \mathrm{mph} \quad \frac{2000}{500}=4\)horas Vento contrário \(450-50=400 \mathrm{mph} \quad \frac{2000}{400}=5\)horas Os horários aumentam as\(9\) horas, então ele verifica. |
A velocidade da corrente de jato foi\(50\) mph.
MaryAnne acabou de voltar de uma visita com seus netos no leste. A viagem estava a\(2400\) quilômetros de sua casa e seu tempo total no avião para a viagem de ida e volta foi de\(10\) horas. Se o avião estivesse voando a uma taxa de\(500\) milhas por hora, qual era a velocidade da corrente de jato?
- Resposta
-
A velocidade da corrente de jato foi\(100\) mph.
Gerry acabou de voltar de uma viagem de cross country. A viagem estava a\(3000\) quilômetros de sua casa e seu tempo total no avião para a viagem de ida e volta foi de\(11\) horas. Se o avião estivesse voando a uma taxa de\(550\) milhas por hora, qual era a velocidade da corrente de jato?
- Resposta
-
A velocidade da corrente de jato foi\(50\) mph.
Os aplicativos de trabalho também podem ser modelados por equações quadráticas. Vamos configurá-los usando os mesmos métodos que usamos quando os resolvemos com equações racionais. Usaremos um cenário semelhante agora.
A revista semanal de fofocas tem uma grande história sobre a eleição presidencial e o editor quer que a revista seja impressa o mais rápido possível. Ela pediu à impressora que usasse uma impressora extra para que a impressão fosse feita mais rapidamente. Pressione #1 leva mais\(12\) horas do que pressionar #2 para fazer o trabalho e, quando as duas impressoras estão funcionando, elas podem imprimir o trabalho em\(8\) horas. Quanto tempo leva para cada impressora imprimir o trabalho sozinha?
Solução:
Isso é um problema de trabalho. Um gráfico nos ajudará a organizar as informações.
Estamos procurando quantas horas cada impressora levaria separadamente para concluir o trabalho.
| Deixe\(x=\) o número de horas para pressionar #2 para concluir o trabalho. Insira as horas por trabalho em Press #1, Press #2 e quando eles trabalham juntos. |
 |
| A peça concluída pelo Press #1 mais a peça concluída pela Press #2 é igual à quantidade concluída em conjunto. Traduza para uma equação. |
 |
| Resolver. | 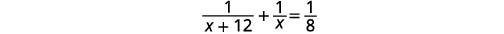 |
| Multiplique pelo LCD, 8\(x(x+12)\). | 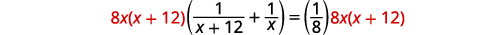 |
| Simplifique. | 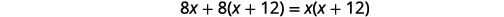
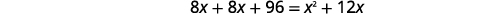

|
| Resolver. | 
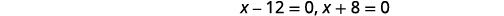

|
| Como a ideia de horas negativas não faz sentido, usamos os valores\(x=12\). | 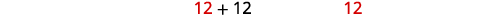
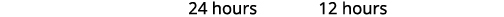
|
| Escreva nossa resposta de frase. | Pressione #1 levaria\(24\) horas e pressione #2 levaria\(12\) horas para fazer o trabalho sozinho. |
A revista semanal de notícias tem uma grande história com o nome de Pessoa do Ano e o editor quer que a revista seja impressa o mais rápido possível. Ela pediu à impressora que usasse uma impressora extra para que a impressão fosse feita mais rapidamente. Pressione #1 leva mais\(6\) horas do que pressionar #2 para fazer o trabalho e, quando as duas impressoras estão funcionando, elas podem imprimir o trabalho em\(4\) horas. Quanto tempo leva para cada impressora imprimir o trabalho sozinha?
- Resposta
-
Pressione #1 levaria\(12\) horas e pressione #2 levaria\(6\) horas para fazer o trabalho sozinho.
Erlinda está dando uma festa e quer encher sua banheira de hidromassagem. Se ela usa apenas a mangueira vermelha, leva\(3\) horas a mais do que se ela usar apenas a mangueira verde. Se ela usar as duas mangueiras juntas, a banheira de hidromassagem se enche em\(2\) horas. Quanto tempo leva para cada mangueira encher a banheira de hidromassagem?
- Resposta
-
A mangueira vermelha leva\(6\) horas e a mangueira verde leva\(3\) horas sozinha.
Acesse esses recursos on-line para obter instruções e práticas adicionais com a resolução de aplicativos modelados por equações quadráticas.
Conceitos-chave
- Métodos para resolver equações quadráticas
- Fatorar
- Propriedade de raiz quadrada
- Completando a Praça
- Fórmula quadrática
- Como usar uma estratégia de resolução de problemas.
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que estamos procurando.
- Diga o que estamos procurando. Escolha uma variável para representar essa quantidade.
- Traduza em uma equação. Pode ser útil reafirmar o problema em uma frase com todas as informações importantes. Em seguida, traduza a frase em inglês em uma equação de álgebra.
- Resolva a equação usando boas técnicas de álgebra.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
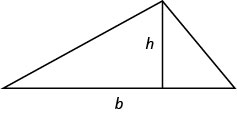
- Área de um triângulo
- Para um triângulo com base,\(b\), e altura\(h\),, a área\(A\),, é dada pela fórmula\(A=\frac{1}{2}bh\).
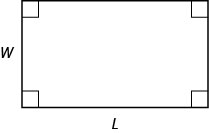
- Área de um retângulo
- Para um retângulo com comprimento,\(L\), e largura\(W\),, a área\(A\),, é dada pela fórmula\(A=LW\).
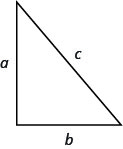
- Teorema de Pitágoras
- Em qualquer triângulo reto, onde\(a\) e\(b\) estão os comprimentos das pernas, e\(c\) é o comprimento da hipotenusa,\(a^{2}+b^{2}=c^{2}\).
- movimento de projétil
- A altura em pés\(h\),, de um objeto lançado no ar com velocidade inicial,\(v_{0}\), após\(t\) segundos é dada pela fórmula\(h=-16 t^{2}+v_{0} t\).


