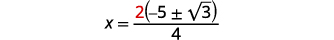9.4: Resolva equações quadráticas usando a fórmula quadrática
- Page ID
- 183554
Ao final desta seção, você poderá:
- Resolva equações quadráticas usando a fórmula quadrática
- Use o discriminante para prever o número e o tipo de soluções de uma equação quadrática
- Identifique o método mais apropriado a ser usado para resolver uma equação quadrática
Antes de começar, faça este teste de prontidão.
- Avalie\(b^{2}-4 a b\) quando\(a=3\)\(b=−2\) e.
- Simplifique\(\sqrt{108}\).
- Simplifique\(\sqrt{50}\).
Resolva equações quadráticas usando a fórmula quadrática
Quando resolvemos equações quadráticas na última seção completando o quadrado, sempre demos os mesmos passos. Ao final do conjunto de exercícios, você deve estar se perguntando “não há uma maneira mais fácil de fazer isso?” A resposta é “sim”. Os matemáticos buscam padrões quando fazem coisas repetidamente para facilitar seu trabalho. Nesta seção, derivaremos e usaremos uma fórmula para encontrar a solução de uma equação quadrática.
Já vimos como resolver uma fórmula para uma variável específica 'em geral', para que façamos as etapas algébricas apenas uma vez e, em seguida, usássemos a nova fórmula para encontrar o valor da variável específica. Agora, passaremos pelas etapas de completar o quadrado usando a forma geral de uma equação quadrática para resolver uma equação quadrática para\(x\).
Começamos com a forma padrão de uma equação quadrática e a resolvemos\(x\) completando o quadrado.
| \(ax^2 + bx + c = 0, \quad a \ne 0\) | |
| Isole os termos variáveis em um lado. | \(ax^2 + bx \quad = -c\) |
| Faça o coeficiente de\(x^{2}\) igual a\(1\), dividindo por\(a\). | \(\dfrac{ax^2}{a} + \dfrac{b}{a}x \quad = -\dfrac{c}{a}\) |
| Simplifique. | \(x^2+ \dfrac{b}{a}x \quad = -\dfrac{c}{a}\) |
| Para completar o quadrado, encontre\(\left(\dfrac{1}{2} \cdot \dfrac{b}{a}\right)^{2}\) e adicione-o aos dois lados da equação. | |
| \(\left(\dfrac{1}{2} \dfrac{b}{a}\right)^{2}=\dfrac{b^{2}}{4 a^{2}}\) | \(x^2 + \dfrac{b}{a}x +{\color{red}{\dfrac{b^2}{4a^2}}}{\color{black}{ = -\dfrac{c}{a}\,+\,}}{\color{red}{\dfrac{b^2}{4a^2}}}\) |
| O lado esquerdo é um quadrado perfeito, considere-o. | \(\left( x + \dfrac{b}{2a}\right)^2 = -\dfrac{c}{a}+\dfrac{b^2}{4a^2}\) |
| Encontre o denominador comum do lado direito e escreva frações equivalentes com o denominador comum. | \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2}{4a^2}-\dfrac{c\cdot\color{red}{4a}}{a\cdot\color{red}{4a}}\) |
| Simplifique. | \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2}{4a^2}-\dfrac{4ac}{4a^2}\) |
| Combine em uma fração. | \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2-4ac}{4a^2}\) |
| Use a propriedade raiz quadrada. | \(x + \dfrac{b}{2a}= \pm\sqrt{\dfrac{b^2-4ac}{4a^2}}\) |
| Simplifique o radical. | \(x + \dfrac{b}{2a}= \pm\dfrac{\sqrt{b^2-4ac}}{2a}\) |
| Adicione\(-\dfrac{b}{2a}\) aos dois lados da equação. | \(x = -\dfrac{b}{2a} \pm\dfrac{\sqrt{b^2-4ac}}{2a}\) |
| Combine os termos no lado direito. | \(x = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\) |
A equação final é chamada de “Fórmula quadrática”.
As soluções para uma equação quadrática da forma\(a x^{2}+b x+c=0\), onde\(a≠0\) são dadas pela fórmula:
\[x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \label{quad}\]
Para usar a Fórmula Quadrática, substituímos os valores\(c\) de\(a,b\) e da forma padrão pela expressão no lado direito da fórmula. Em seguida, simplificamos a expressão. O resultado é o par de soluções para a equação quadrática.
Observe que a fórmula quadrática (Equação\ ref {quad}) é uma equação. Certifique-se de usar os dois lados da equação.
Resolva usando a fórmula quadrática:\(2 x^{2}+9 x-5=0\).
Solução:
| Etapa 1: Escreva a equação quadrática na forma padrão. Identifique os\(a,b,c\) valores. | Essa equação está na forma padrão. | \(\begin{aligned} \color{red}{a x^{2}+b x+c =0} \\ 2 x^{2}+9 x-5 =0 \\ a=2, b =9, c=-5 \end{aligned}\) |
| Etapa 2: Escreva a fórmula quadrática. Em seguida, substitua os valores de\(a,b,c\). | Substituir em\(a=2, b=9, c=-5\) | \(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) \(x=\dfrac{-9 \pm \sqrt{9^{2}-4 \cdot 2 \cdot(-5)}}{2 \cdot 2}\) |
| Etapa 3: Simplifique a fração e resolva\(x\). | \(\begin{array}{l}{x=\dfrac{-9 \pm \sqrt{81-(-40)}}{4}} \\ {x=\dfrac{-9 \pm \sqrt{121}}{4}} \\ {x=\dfrac{-9 \pm 11}{4}} \\ {x=\dfrac{-9+11}{4}}\quad x=\dfrac{-9-11}{4} \\ {x=\dfrac{2}{4} \quad \quad\:\:\: x=\dfrac{-20}{4}}\\ {x=\dfrac{1}{2} \quad\quad\:\:\: x=-5}\end{array}\) | |
| Etapa 4: verifique as soluções. | Coloque cada resposta na equação original para verificar. \(x=\color{red}{\dfrac{1}{2}}\)Substitua\(x=\color{red}{-5}\) e. |
\(\begin{aligned}2 x^{2}+9 x-5&=0 \\ 2\color{black}{\left(\color{red}{\dfrac{1}{2}}\right)}^{2}+9 \cdot \color{red}{\dfrac{1}{2}}\color{black}{-}5 &\stackrel{?}{=} 0 \\ 2\cdot\dfrac{1}{4}+0\cdot\dfrac{1}{2}-5&\stackrel{?}{=}0 \\ 2\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{2}-5&\stackrel{?}{=}0 \\ \dfrac{1}{2}+\dfrac{9}{2}-5&\stackrel{?}{=}0 \\ \dfrac{10}{2}-5&\stackrel{?}{=}0 \\5-5&\stackrel{?}{=}0\\0&=0\end{aligned}\) \(\begin{array}{r}{2 x^{2}+9 x-5=0} \\ {2(\color{red}{-5}\color{black}{)}^{2}+9(\color{red}{-5}\color{black}{)}-5\stackrel{?}{=}0} \\ {2 \cdot 25-45-5\stackrel{?}{=}0} \\ {50-45-5\stackrel{?}{=}0} \\ {0=0}\end{array}\) |
Resolva usando a fórmula quadrática:\(3 y^{2}-5 y+2=0\).
- Responda
-
\(y=1, y=\dfrac{2}{3}\)
Resolva usando a fórmula quadrática:\(4 z^{2}+2 z-6=0\).
- Responda
-
\(z=1, z=-\dfrac{3}{2}\)
- Escreva a equação quadrática na forma padrão,\(a x^{2}+b x+c=0\). Identifique os valores de\(a,b\),\(c\) e.
- Escreva a fórmula quadrática. Em seguida, substitua os valores de\(a,b\),\(c\) e.
- Simplifique.
- Verifique as soluções.
Se você disser a fórmula à medida que a escreve em cada problema, você a memorizará em pouco tempo! E lembre-se, a Fórmula Quadrática é uma EQUAÇÃO. Certifique-se de começar com “\(x=\)”.
Resolva usando a fórmula quadrática:\(x^{2}-6 x=-5\).
Solução:
|
\(x^{2}-6 x=-5\) |
|
| Escreva a equação na forma padrão adicionando\(5\) em cada lado. |
\(x^{2}-6 x+5=0\) |
| Essa equação agora está na forma padrão. |
\({\color{red}{\small{ax^2+bx + c} = \small{0}}}\) |
| Identifique os valores de\(\color{cyan}a\),\(\color{red}b\),\(\color{limegreen}c\). | \({\color{cyan}a=1}\),\({\color{red}b=-6}\),\({\color{limegreen}c=5}\) |
| Escreva a fórmula quadrática. |
\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) |
| Em seguida, substitua os valores de\(a, b, c\). |
\(x=\dfrac{-\color{red} (-6 ) \color{black} \pm \sqrt{\color{red}(-6) \color{black}^{2}-4 \cdot \color{cyan}1 \color{black} \cdot ( \color{limegreen}5 \color{black})}}{2 \cdot \color{cyan} 1} \) |
| Simplifique. |
\(x=\dfrac{6 \pm \sqrt{36-20}}{2}\) \(x=\dfrac{6 \pm \sqrt{16}}{2}\) \(x=\dfrac{6 \pm 4}{2}\) |
| Reescreva para mostrar duas soluções. |
\(x=\frac{6+4}{2}, \quad x=\frac{6-4}{2}\) |
| Simplifique. |
\(x=\frac{10}{2}, \quad x=\frac{2}{2}\) |
| \(x=5, \quad x=1\) | |
|
Confira: 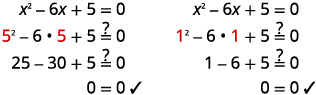 |
Resolva usando a fórmula quadrática:\(a^{2}-2 a=15\).
- Responda
-
\(a=-3, a=5\)
Resolva usando a fórmula quadrática:\(b^{2}+24=-10 b\).
- Responda
-
\(b=-6, b=-4\)
Quando resolvemos equações quadráticas usando a propriedade de raiz quadrada, às vezes obtivemos respostas que tinham radicais. Isso também pode acontecer ao usar a Fórmula Quadrática. Se obtivermos um radical como solução, a resposta final deve ter o radical em sua forma simplificada.
Resolva usando a fórmula quadrática:\(2 x^{2}+10 x+11=0\).
Solução:
 |
|
| Essa equação está na forma padrão. |  |
| Identifique os valores de\(a,b\)\(c\) e. |  |
| Escreva a fórmula quadrática. |
\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) |
| Em seguida, substitua os valores de\(a, b\),\(c\) e. | 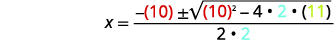 |
| Simplifique. |
\(x=\dfrac{-10 \pm \sqrt{100-88}}{4}\) |
|
\(x=\dfrac{-10 \pm \sqrt{12}}{4}\) |
|
| Simplifique o radical. |
\(x=\dfrac{-10 \pm 2 \sqrt{3}}{4}\) |
| Considere o fator comum no numerador. |
\(x=\dfrac{\color{red}{2}(-5 \pm \sqrt{3})}{4}\) |
| Remova os fatores comuns. |
\(x=\dfrac{-5 \pm \sqrt{3}}{2}\) |
| Reescreva para mostrar duas soluções. |
\(x=\dfrac{-5+\sqrt{3}}{2}, \quad x=\dfrac{-5-\sqrt{3}}{2}\) |
|
Confira: Deixamos o cheque para você! |
Resolva usando a fórmula quadrática:\(3 m^{2}+12 m+7=0\).
- Responda
-
\(m=\dfrac{-6+\sqrt{15}}{3}, m=\dfrac{-6-\sqrt{15}}{3}\)
Resolva usando a fórmula quadrática:\(5 n^{2}+4 n-4=0\).
- Responda
-
\(n=\dfrac{-2+2 \sqrt{6}}{5}, n=\dfrac{-2-2 \sqrt{6}}{5}\)
Quando\(a, b\) substituímos e\(c\) entramos na Fórmula Quadrática e o radicando é negativo, a equação quadrática terá soluções imaginárias ou complexas. Veremos isso no próximo exemplo.
Resolva usando a fórmula quadrática:\(3 p^{2}+2 p+9=0\).
Solução:
 |
|
| Essa equação está na forma padrão. |  |
| Identifique os valores de\(a,b,c\). |  |
| Escreva a fórmula quadrática. | 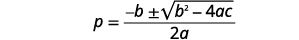 |
| Em seguida, substitua os valores de\(a,b,c\). | 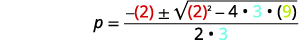 |
| Simplifique. | 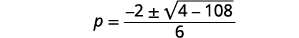 |
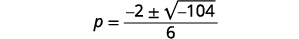 |
|
| Simplifique o radical usando números complexos. | 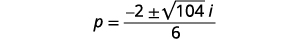 |
| Simplifique o radical. | 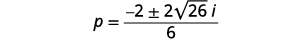 |
| Fator o fator comum no numerador. | 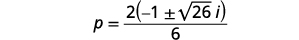 |
| Remova os fatores comuns. | 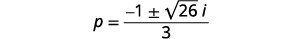 |
| Reescreva no\(a+bi\) formato padrão. | 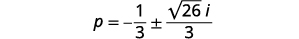 |
| Escreva como duas soluções. | 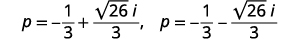 |
Resolva usando a fórmula quadrática:\(4 a^{2}-2 a+8=0\).
- Responda
-
\(a=\dfrac{1}{4}+\dfrac{\sqrt{31}}{4} i, \quad a=\dfrac{1}{4}-\dfrac{\sqrt{31}}{4} i\)
Resolva usando a fórmula quadrática:\(5 b^{2}+2 b+4=0\).
- Responda
-
\(b=-\dfrac{1}{5}+\dfrac{\sqrt{19}}{5} i, \quad b=-\dfrac{1}{5}-\dfrac{\sqrt{19}}{5} i\)
Lembre-se de que, para usar a Fórmula Quadrática, a equação deve ser escrita na forma padrão,\(a x^{2}+b x+c=0\). Às vezes, precisaremos fazer alguma álgebra para colocar a equação na forma padrão antes de podermos usar a Fórmula Quadrática.
Resolva usando a fórmula quadrática:\(x(x+6)+4=0\).
Solução:
Nosso primeiro passo é obter a equação na forma padrão.
 |
|
| Distribua para obter a equação na forma padrão. |  |
| Essa equação agora está na forma padrão. |  |
| Identifique os valores de\(a,b,c\). |  |
| Escreva a fórmula quadrática. | 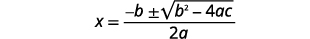 |
| Em seguida, substitua os valores de\(a,b,c\). | 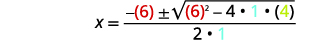 |
| Simplifique. | 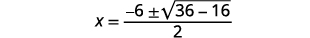 |
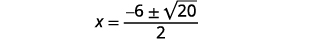 |
|
| Simplifique o radical. | 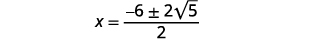 |
| Fator o fator comum no numerador. | 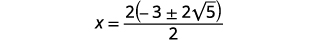 |
| Remova os fatores comuns. | 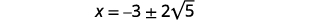 |
| Escreva como duas soluções. | 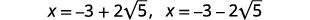 |
|
Confira: Deixamos o cheque para você! |
Resolva usando a fórmula quadrática:\(x(x+2)−5=0\).
- Responda
-
\(x=-1+\sqrt{6}, x=-1-\sqrt{6}\)
Resolva usando a fórmula quadrática:\(3y(y−2)−3=0\).
- Responda
-
\(y=1+\sqrt{2}, y=1-\sqrt{2}\)
Quando resolvemos equações lineares, se uma equação tivesse muitas frações, eliminamos as frações multiplicando os dois lados da equação pelo LCD. Isso nos deu uma equação equivalente — sem frações — para resolver. Podemos usar a mesma estratégia com equações quadráticas.
Resolva usando a fórmula quadrática:\(\dfrac{1}{2} u^{2}+\dfrac{2}{3} u=\dfrac{1}{3}\).
Solução:
Nosso primeiro passo é limpar as frações.
 |
|
| Multiplique os dois lados pelo LCD,\(6\), para limpar as frações. | 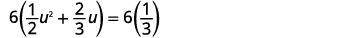 |
| Multiplique. |  |
| Subtraia\(2\) para obter a equação na forma padrão. |  |
| Identifique os valores de\(a, b\),\(c\) e. |  |
| Escreva a fórmula quadrática. | 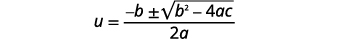 |
| Em seguida, substitua os valores de\(a, b,\)\(c\) e. | 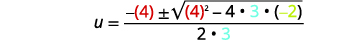 |
| Simplifique. | 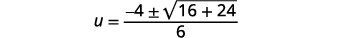 |
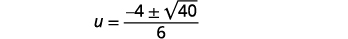 |
|
| Simplifique o radical. | 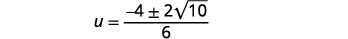 |
| Fator o fator comum no numerador. | 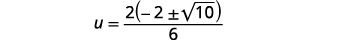 |
| Remova os fatores comuns. | 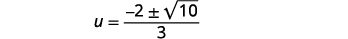 |
| Reescreva para mostrar duas soluções. | 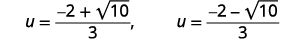 |
|
Confira: Deixamos o cheque para você! |
Resolva usando a fórmula quadrática:\(\dfrac{1}{4} c^{2}-\dfrac{1}{3} c=\dfrac{1}{12}\).
- Responda
-
\(c=\dfrac{2+\sqrt{7}}{3}, \quad c=\dfrac{2-\sqrt{7}}{3}\)
Resolva usando a fórmula quadrática:\(\dfrac{1}{9} d^{2}-\dfrac{1}{2} d=-\dfrac{1}{3}\).
- Responda
-
\(d=\dfrac{9+\sqrt{33}}{4}, d=\dfrac{9-\sqrt{33}}{4}\)
Pense na equação\((x-3)^{2}=0\). Sabemos pela Propriedade do Produto Zero que essa equação tem apenas uma solução,\(x=3\).
Veremos no próximo exemplo como usar a Fórmula Quadrática para resolver uma equação cuja forma padrão é um trinômio quadrado perfeito igual a\(0\) fornece apenas uma solução. Observe que, uma vez simplificado, o radicando se torna\(0\), o que leva a apenas uma solução.
Resolva usando a fórmula quadrática:\(4 x^{2}-20 x=-25\).
Solução:
 |
|
| Adicione\(25\) para obter a equação na forma padrão. |  |
| Identifique os valores de\(a, b\),\(c\) e. |  |
| Escreva a fórmula quadrática. | 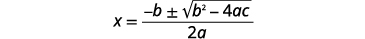 |
| Em seguida, substitua os valores de\(a, b\),\(c\) e. |  |
| Simplifique. | 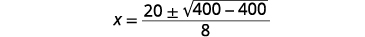 |
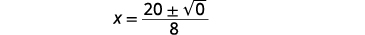 |
|
| Simplifique o radical. |  |
| Simplifique a fração. |  |
|
Confira: Deixamos o cheque para você! |
Você reconheceu que\(4 x^{2}-20 x+25\) é um trinômio quadrado perfeito. É equivalente a\((2 x-5)^{2}\)? Se você resolver\(4 x^{2}-20 x+25=0\) por fatoração e depois usar a propriedade de raiz quadrada, obterá o mesmo resultado?
Resolva usando a fórmula quadrática:\(r^{2}+10 r+25=0\).
- Responda
-
\(r=-5\)
Resolva usando a fórmula quadrática:\(25 t^{2}-40 t=-16\).
- Responda
-
\(t=\dfrac{4}{5}\)
Use o discriminante para prever o número e o tipo de soluções de uma equação quadrática
Quando resolvemos as equações quadráticas nos exemplos anteriores, às vezes obtivemos duas soluções reais, uma solução real e às vezes duas soluções complexas. Existe uma maneira de prever o número e o tipo de soluções para uma equação quadrática sem realmente resolver a equação?
Sim, a expressão sob o radical da Fórmula Quadrática facilita a determinação do número e do tipo de soluções. Essa expressão é chamada de discriminante.
Discriminante

Vamos ver o discriminante das equações em alguns dos exemplos e o número e o tipo de soluções para essas equações quadráticas.
| Equação quadrática (na forma padrão) | Discriminante\(b^{2}-4ac\) | Valor do discriminante | Número e tipo de soluções |
|---|---|---|---|
| \(2 x^{2}+9 x-5=0\) | \ (b^ {2} -4ac\) ">\(\begin{aligned} 9^{2}-& 4 \cdot 2(-5) \\ & 121 \end{aligned}\) | \(+\) | \(2\)real |
| \(4 x^{2}-20 x+25=0\) | \ (b^ {2} -4ac\) ">\((-20)^{2}-4 \cdot 4 \cdot 25\) \(0\) |
\(0\) | \(1\)real |
| \(3 p^{2}+2 p+9=0\) | \ (b^ {2} -4ac\) ">\(2^{2}-4 \cdot 3 \cdot 9\) \(-104\) |
\(-\) | \(2\)complexo |

Usando o discriminante\(b^{2}-4ac\), para determinar o número e o tipo de soluções de uma equação quadrática
Para uma equação quadrática da forma\(ax^{2}+bx+c=0\)\(a \neq 0\),
- Se\(b^{2}-4 a c>0\), a equação tem soluções\(2\) reais.
- se\(b^{2}-4 a c=0\), a equação tem uma solução\(1\) real.
- se\(b^{2}-4 a c<0\), a equação tem soluções\(2\) complexas.
Determine o número de soluções para cada equação quadrática.
- \(3 x^{2}+7 x-9=0\)
- \(5 n^{2}+n+4=0\)
- \(9 y^{2}-6 y+1=0\)
Solução:
Para determinar o número de soluções de cada equação quadrática, examinaremos seu discriminante.
uma.
\(3 x^{2}+7 x-9=0\)
A equação está na forma padrão\(a, b\), identifique\(c\) e.
\(a=3, \quad b=7, \quad c=-9\)
Escreva o discriminante.
\(b^{2}-4 a c\)
Substitua os valores de\(a, b\),\(c\) e.
\((7)^{2}-4 \cdot 3 \cdot(-9)\)
Simplifique.
\(49+108\)
\(157\)
Como o discriminante é positivo, existem soluções\(2\) reais para a equação.
b.
\(5 n^{2}+n+4=0\)
A equação está na forma padrão\(a, b\), identifique\(c\) e.
\(a=5, \quad b=1, \quad c=4\)
Escreva o discriminante.
\(b^{2}-4 a c\)
Substitua os valores de\(a, b\),\(c\) e.
\((1)^{2}-4 \cdot 5 \cdot 4\)
Simplifique.
\(1-80\)
\(-79\)
Como o discriminante é negativo, existem soluções\(2\) complexas para a equação.
c.
\(9 y^{2}-6 y+1=0\)
A equação está na forma padrão\(a, b\), identifique\(c\) e.
\(a=9, \quad b=-6, \quad c=1\)
Escreva o discriminante.
\(b^{2}-4 a c\)
Substitua os valores de\(a, b\),\(c\) e.
\((-6)^{2}-4 \cdot 9 \cdot 1\)
Simplifique.
\(36-36\)
\(0\)
Como o discriminante é\(0\), existe uma solução\(1\) real para a equação.
Determine o número e o tipo de soluções para cada equação quadrática.
- \(8 m^{2}-3 m+6=0\)
- \(5 z^{2}+6 z-2=0\)
- \(9 w^{2}+24 w+16=0\)
- Responda
-
- \(2\)soluções complexas
- \(2\)soluções reais
- \(1\)solução real
Determine o número e o tipo de soluções para cada equação quadrática.
- \(b^{2}+7 b-13=0\)
- \(5 a^{2}-6 a+10=0\)
- \(4 r^{2}-20 r+25=0\)
- Responda
-
- \(2\)soluções reais
- \(2\)soluções complexas
- \(1\)solução real
Identifique o método mais apropriado a ser usado para resolver uma equação quadrática
Resumimos os quatro métodos que usamos para resolver equações quadráticas abaixo.
Métodos para resolver equações quadráticas
- Fatorar
- Propriedade de raiz quadrada
- Completando a Praça
- Fórmula quadrática
Dado que temos quatro métodos a serem usados para resolver uma equação quadrática, como você decide qual deles usar? A fatoração costuma ser o método mais rápido e, por isso, tentamos primeiro. Se a equação for\(ax^{2}=k\) ou\(a(x−h)^{2}=k\) usarmos a propriedade de raiz quadrada. Para qualquer outra equação, provavelmente é melhor usar a Fórmula Quadrática. Lembre-se de que você pode resolver qualquer equação quadrática usando a Fórmula Quadrática, mas esse nem sempre é o método mais fácil.
E quanto ao método de completar o quadrado? A maioria das pessoas acha esse método complicado e prefere não usá-lo. Precisávamos incluí-lo na lista de métodos porque completamos o quadrado em geral para derivar a Fórmula Quadrática. Você também usará o processo de completar o quadrado em outras áreas da álgebra.
Identifique o método mais apropriado para resolver uma equação quadrática
- Experimente o Factoring primeiro. Se os fatores quadráticos forem fáceis, esse método é muito rápido.
- Experimente a propriedade Square Root em seguida. Se a equação se encaixa na forma\(ax^{2}=k\) ou\(a(x−h)^{2}=k\), ela pode ser facilmente resolvida usando a propriedade de raiz quadrada.
- Use a fórmula quadrática. Qualquer outra equação quadrática é melhor resolvida usando a Fórmula Quadrática.
O próximo exemplo usa essa estratégia para decidir como resolver cada equação quadrática.
Identifique o método mais apropriado a ser usado para resolver cada equação quadrática.
- \(5 z^{2}=17\)
- \(4 x^{2}-12 x+9=0\)
- \(8 u^{2}+6 u=11\)
Solução:
uma.
\(5z^{2}=17\)
Como a equação está no\(ax^{2}=k\), o método mais apropriado é usar a propriedade de raiz quadrada.
b.
\(4 x^{2}-12 x+9=0\)
Reconhecemos que o lado esquerdo da equação é um trinômio quadrado perfeito e, portanto, a fatoração será o método mais apropriado.
c.
\(8 u^{2}+6 u=11\)
Coloque a equação na forma padrão.
\(8 u^{2}+6 u-11=0\)
Embora nosso primeiro pensamento seja tentar fatorar, pensar em todas as possibilidades do método de tentativa e erro nos leva a escolher a Fórmula Quadrática como o método mais apropriado.
Identifique o método mais apropriado a ser usado para resolver cada equação quadrática.
- \(x^{2}+6 x+8=0\)
- \((n-3)^{2}=16\)
- \(5 p^{2}-6 p=9\)
- Responda
-
- Fatorar
- Propriedade de raiz quadrada
- Fórmula quadrática
Identifique o método mais apropriado a ser usado para resolver cada equação quadrática.
- \(8 a^{2}+3 a-9=0\)
- \(4 b^{2}+4 b+1=0\)
- \(5 c^{2}=125\)
- Responda
-
- Fórmula quadrática
- Fatoração ou propriedade de raiz quadrada
- Propriedade de raiz quadrada
Acesse esses recursos on-line para obter instruções e práticas adicionais com o uso da Fórmula Quadrática.
Conceitos chave
- Fórmula quadrática
- As soluções para uma equação quadrática da forma\(a x^{2}+b x+c=0, a \neq 0\) são dadas pela fórmula:
\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
- As soluções para uma equação quadrática da forma\(a x^{2}+b x+c=0, a \neq 0\) são dadas pela fórmula:
- Como resolver uma equação quadrática usando a fórmula quadrática.
- Escreva a equação quadrática na forma padrão,\(a x^{2}+b x+c=0\). Identifique os valores de\(a, b, c\).
- Escreva a fórmula quadrática. Em seguida, substitua os valores de\(a, b, c\).
- Simplifique.
- Verifique as soluções.
- Usando o discriminante,\(b^{2}-4 a c\), para determinar o número e o tipo de soluções de uma equação quadrática
- Para uma equação quadrática da forma\(a x^{2}+b x+c=0, a \neq 0\),
- Se\(b^{2}-4 a c>0\), a equação tem soluções\(2\) reais.
- Se\(b^{2}-4 a c=0\), a equação tem uma solução\(1\) real.
- Se\(b^{2}-4 a c<0\), a equação tem soluções\(2\) complexas.
- Para uma equação quadrática da forma\(a x^{2}+b x+c=0, a \neq 0\),
- Métodos para resolver equações quadráticas:
- Fatorar
- Propriedade de raiz quadrada
- Completando a Praça
- Fórmula quadrática
- Como identificar o método mais adequado para resolver uma equação quadrática.
- Experimente o Factoring primeiro. Se os fatores quadráticos forem fáceis, esse método é muito rápido.
- Experimente a propriedade Square Root em seguida. Se a equação se encaixa na forma\(a x^{2}=k\) ou\(a(x-h)^{2}=k\), ela pode ser facilmente resolvida usando a propriedade de raiz quadrada.
- Use a fórmula quadrática. Qualquer outra equação quadrática é melhor resolvida usando a Fórmula Quadrática.
Glossário
- discriminante
- Na Fórmula Quadrática\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\), a quantidade\(b^{2}-4 a c\) é chamada de discriminante.