9.2: Resolva equações quadráticas usando a propriedade de raiz quadrada
- Page ID
- 183509
Ao final desta seção, você poderá:
- Resolva equações quadráticas da forma\(ax^{2}=k\) usando a propriedade de raiz quadrada
- Resolva equações quadráticas da forma\(a(x–h)^{2}=k\) usando a propriedade de raiz quadrada
Antes de começar, faça este teste de prontidão.
- Simplifique:\(\sqrt{128}\).
Se você perdeu esse problema, consulte o Exemplo 8.13. - Simplifique:\(\sqrt{\frac{32}{5}}\).
Se você perdeu esse problema, consulte o Exemplo 8.50. - Fator:\(9 x^{2}-12 x+4\).
Se você perdeu esse problema, consulte o Exemplo 6.23.
Uma equação quadrática é uma equação da forma\(a x^{2}+b x+c=0\), onde\(a≠0\). As equações quadráticas diferem das equações lineares ao incluir um termo quadrático com a variável elevada à segunda potência da forma\(ax^{2}\). Usamos métodos diferentes para resolver equações quadráticas do que equações lineares, porque apenas adicionar, subtrair, multiplicar e dividir termos não isolará a variável.
Vimos que algumas equações quadráticas podem ser resolvidas por fatoração. Neste capítulo, aprenderemos três outros métodos a serem usados caso uma equação quadrática não possa ser fatorada.
Resolva equações quadráticas da forma\(ax^{2}=k\) usando a propriedade de raiz quadrada
Já resolvemos algumas equações quadráticas por fatoração. Vamos analisar como usamos a fatoração para resolver a equação quadrática\(x^{2}=9\).
\(x^{2}=9\)
Coloque a equação na forma padrão.
\(x^{2}-9=0\)
Fator a diferença dos quadrados.
\((x-3)(x+3)=0\)
Use a propriedade Zero Produce.
\(x-3=0 \quad x-3=0\)
Resolva cada equação.
\(x=3 \quad x=-3\)
Podemos facilmente usar a fatoração para encontrar as soluções de equações semelhantes, como\(x^{2}=16\) e\(x^{2}=25\), porque\(16\) e\(25\) são quadrados perfeitos. Em cada caso, obteríamos duas soluções\(x=4, x=-4\) e\(x=5, x=-5\)
Mas o que acontece quando temos uma equação como essa\(x^{2}=7\)? Como não\(7\) é um quadrado perfeito, não podemos resolver a equação fatorando.
Anteriormente, aprendemos que, uma vez que\(169\) é o quadrado de\(13\), também podemos dizer que\(13\) é uma raiz quadrada de\(169\). Além disso\((-13)^{2}=169\),, também\(−13\) é uma raiz quadrada de\(169\). Portanto, ambos\(13\) e\(−13\) são raízes quadradas de\(169\). Então, todo número positivo tem duas raízes quadradas — uma positiva e uma negativa. Anteriormente, definimos a raiz quadrada de um número desta forma:
Se\(n^{2}=m\), então\(n\) é uma raiz quadrada de\(m\).
Como essas equações são todas da forma\(x^{2}=k\), a definição da raiz quadrada nos diz que as soluções são as duas raízes quadradas de\(k\). Isso leva à propriedade Square Root.
Propriedade de raiz quadrada
Se\(x^{2}=k\), então
\(x=\sqrt{k} \quad\)ou\(\quad x=-\sqrt{k} \quad\) ou\(\quad x=\pm \sqrt{k}\)
Observe que a propriedade de raiz quadrada fornece duas soluções para uma equação da forma\(x^{2}=k\), a raiz quadrada principal de\(k\) e sua oposta. Também poderíamos escrever a solução como\(x=\pm \sqrt{k}\). Lemos isso como\(x\) positivo ou negativo na raiz quadrada de\(k\).
Agora resolveremos a equação\(x^{2}=9\) novamente, desta vez usando a propriedade de raiz quadrada.
\(\begin{aligned} &x^{2} =9 \\ \text { Use the Square Root Property. } \quad& x=\pm \sqrt{9} \\& x =\pm 3 \end{aligned}\)
Então,\(x=3\) ou\(x=-3\)
O que acontece quando a constante não é um quadrado perfeito? Vamos usar a propriedade de raiz quadrada para resolver a equação\(x^{2}=7\).
\(x^{2}=7\)
Use a propriedade Square Root. \(x=\sqrt{7}, \quad x=-\sqrt{7}\)
Não podemos simplificar\(\sqrt{7}\), então deixamos a resposta como radical.
Resolver:\(x^{2}-50=0\).
Solução:
| Etapa 1: Isole o termo quadrático e torne seu coeficiente um. | Adicione\(50\) aos dois lados para ficar\(x^{2}\) sozinho. | \(\begin{aligned} x^{2}-50 &=0 \\ x^{2} &=50 \end{aligned}\) |
| Etapa 2: Use a propriedade Square Root. | Lembre-se de escrever o\(\pm\) símbolo. | \(x=\pm \sqrt{50}\) |
| Etapa 3: Simplifique o radical. | Reescreva para mostrar duas soluções. | \(\begin{array}{l}{x=\pm \sqrt{25} \cdot \sqrt{2}} \\ {x=\pm 5 \sqrt{2}} \\ {}x=5\sqrt{2}, \:x=-5\sqrt{2}\end{array}\) |
| Etapa 4: verifique as soluções. | Substitua em\(x=5 \sqrt{2}\) e\(x=-5 \sqrt{2}\) |
\(\begin{array}{r}{x^{2}-50=0} \\ {(\color{red}{5 \sqrt{2}}\color{black}{)}^{2}-50 \stackrel{?}{=} 0} \\ {25 \cdot 2-50 \stackrel{?}{=} 0} \\ {0=0}\end{array}\) \(\begin{array}{r}{x^{2}-50=0} \\ {(\color{red}{-5 \sqrt{2}}\color{black}{)}^{2}-50 \stackrel{?}{=} 0} \\ {25 \cdot 2-50 \stackrel{?}{=} 0} \\ {0=0}\end{array}\) |
Resolver:\(x^{2}-48=0\).
- Responda
-
\(x=4 \sqrt{3}, x=-4 \sqrt{3}\)
Resolver:\(y^{2}-27=0\).
- Responda
-
\(y=3 \sqrt{3}, y=-3 \sqrt{3}\)
As etapas a serem seguidas para usar a propriedade de raiz quadrada para resolver uma equação quadrática estão listadas aqui.
Resolva uma equação quadrática usando a propriedade de raiz quadrada
- Isole o termo quadrático e torne seu coeficiente um.
- Use a propriedade de raiz quadrada.
- Simplifique o radical.
- Verifique as soluções.
Para usar a propriedade de raiz quadrada, o coeficiente do termo variável deve ser igual a um. No próximo exemplo, devemos dividir os dois lados da equação pelo coeficiente\(3\) antes de usar a propriedade de raiz quadrada.
Resolver:\(3 z^{2}=108\).
Solução:
| \(3 z^{2}=108\) | |
| O termo quadrático é isolado. Divida por\(3\) para fazer seu coeficiente\(1\). | \(\frac{3 z^{2}}{3}=\frac{108}{3}\) |
| Simplifique. | \(z^{2}=36\) |
| Use a propriedade Square Root. | \(z=\pm \sqrt{36}\) |
| Simplifique o radical. | \(z=\pm 6\) |
| Reescreva para mostrar duas soluções. | \(z=6, \quad z=-6\) |
|
Confira as soluções: 
|
Resolver:\(2x^{2}=98\).
- Responda
-
\(x=7, x=-7\)
Resolver:\(5m^{2}=80\).
- Responda
-
\(m=4, m=-4\)
A propriedade de raiz quadrada afirma “Se”\(x^{2}=k\), o que acontecerá se\(k<0\)? Esse será o caso no próximo exemplo.
Resolver:\(x^{2}+72=0\).
Solução:
| \(x^{2}+72=0\) | |
| Isole o termo quadrático. | \(x^{2}=-72\) |
| Use a propriedade Square Root. | \(x=\pm \sqrt{-72}\) |
| Simplifique o uso de números complexos. | \(x=\pm \sqrt{72} i\) |
| Simplifique o radical. | \(x=\pm 6 \sqrt{2} i\) |
| Reescreva para mostrar duas soluções | \(x=6 \sqrt{2} i, x=-6 \sqrt{2} i\) |
|
Confira as soluções: 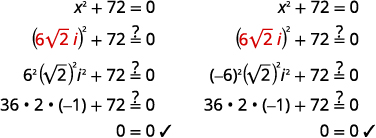
|
Resolver:\(c^{2}+12=0\).
- Responda
-
\(c=2 \sqrt{3} i, \quad c=-2 \sqrt{3} i\)
Resolver:\(q^{2}+24=0\).
- Responda
-
\(c=2 \sqrt{6} i, \quad c=-2 \sqrt{6} i\)
Nosso método também funciona quando frações ocorrem na equação, resolvemos como qualquer equação com frações. No próximo exemplo, primeiro isolamos o termo quadrático e, em seguida, tornamos o coeficiente igual a um.
Resolver:\(\frac{2}{3} u^{2}+5=17\).
Solução:
| \(\frac{2}{3} u^{2}+5=17\) | |
| Isole o termo quadrático. | 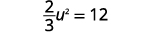 |
| Multiplique por\(\frac{3}{2}\) para fazer o coeficiente\(1\). | 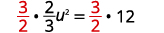 |
| Simplifique. | 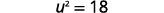 |
| Use a propriedade Square Root. | 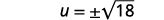 |
| Simplifique o radical. | 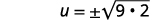 |
| Simplifique. | 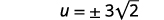 |
| Reescreva para mostrar duas soluções. |  |
|
Confira: 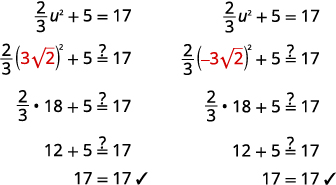
|
Resolver:\(\frac{1}{2} x^{2}+4=24\).
- Responda
-
\(x=2 \sqrt{10}, x=-2 \sqrt{10}\)
Resolver:\(\frac{3}{4} y^{2}-3=18\).
- Responda
-
\(y=2 \sqrt{7}, y=-2 \sqrt{7}\)
As soluções para algumas equações podem ter frações dentro dos radicais. Quando isso acontece, devemos racionalizar o denominador.
Resolver:\(2 x^{2}-8=41\).
Solução:
 |
|
| Isole o termo quadrático. |  |
| Divida por\(2\) para fazer o coeficiente\(1\). | 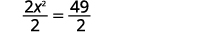 |
| Simplifique. | 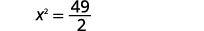 |
| Use a propriedade Square Root. | 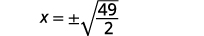 |
| Reescreva o radical como uma fração das raízes quadradas. | 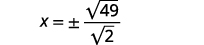 |
| Racionalize o denominador. | 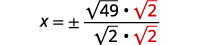 |
| Simplifique. | 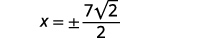 |
| Reescreva para mostrar duas soluções. | 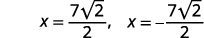 |
|
Confira: Deixamos o cheque para você. |
Resolver:\(5 r^{2}-2=34\).
- Responda
-
\(r=\frac{6 \sqrt{5}}{5}, \quad r=-\frac{6 \sqrt{5}}{5}\)
Resolver:\(3 t^{2}+6=70\).
- Responda
-
\(t=\frac{8 \sqrt{3}}{3}, \quad t=-\frac{8 \sqrt{3}}{3}\)
Resolva a equação quadrática da forma\(a(x-h)^{2}=k\) usando a propriedade de raiz quadrada
Também podemos usar a propriedade de raiz quadrada para resolver uma equação da\(a(x-h)^{2}=k\) forma. Observe que o termo quadrático\(x\),, na forma original\(ax^{2}=k\) é substituído por\((x-h)\).
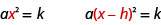
O primeiro passo, como antes, é isolar o termo que tem a variável ao quadrado. Nesse caso, um binômio está sendo quadrado. Uma vez isolado o binômio, dividindo cada lado pelo coeficiente de\(a\), a propriedade de raiz quadrada pode ser usada em\((x-h)^{2}\).
Resolver:\(4(y-7)^{2}=48\).
Solução:
| \(4(y-7)^{2}=48\) | |
| Divida os dois lados pelo coeficiente\(4\). | \((y-7)^{2}=12\) |
| Use a propriedade de raiz quadrada no binômio. | \(y-7=\pm \sqrt{12}\) |
| Simplifique o radical. | \(y-7=\pm 2 \sqrt{3}\) |
| Resolva para\(y\). | \(y=7 \pm 2 \sqrt{3}\) |
| Reescreva para mostrar duas soluções. | \(y=7+2 \sqrt{3}\) \(y=7-2 \sqrt{3}\) |
|
Confira: 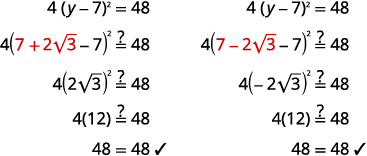
|
Resolver:\(3(a-3)^{2}=54\).
- Responda
-
\(a=3+3 \sqrt{2}, \quad a=3-3 \sqrt{2}\)
Resolver:\(2(b+2)^{2}=80\).
- Responda
-
\(b=-2+2 \sqrt{10}, \quad b=-2-2 \sqrt{10}\)
Lembre-se de que quando pegamos a raiz quadrada de uma fração, podemos pegar a raiz quadrada do numerador e do denominador separadamente.
Resolver:\(\left(x-\frac{1}{3}\right)^{2}=\frac{5}{9}\).
Solução:
\(\left(x-\frac{1}{3}\right)^{2}=\frac{5}{9}\)
Use a propriedade Square Root.
\(x-\frac{1}{3}=\pm \sqrt{\frac{5}{9}}\)
Reescreva o radical como uma fração das raízes quadradas.
\(x-\frac{1}{3}=\pm \frac{\sqrt{5}}{\sqrt{9}}\)
Simplifique o radical.
\(x-\frac{1}{3}=\pm \frac{\sqrt{5}}{3}\)
Resolva para\(x\).
\(x=\frac{1}{3} \pm \frac{\sqrt{5}}{3}\)
Reescreva para mostrar duas soluções.
\(x=\frac{1}{3}+\frac{\sqrt{5}}{3}, x=\frac{1}{3}-\frac{\sqrt{5}}{3}\)
Confira:
Deixamos o cheque para você.
Resolver:\(\left(x-\frac{1}{2}\right)^{2}=\frac{5}{4}\).
- Responda
-
\(x=\frac{1}{2}+\frac{\sqrt{5}}{2}, x=\frac{1}{2}-\frac{\sqrt{5}}{2}\)
Resolver:\(\left(y+\frac{3}{4}\right)^{2}=\frac{7}{16}\).
- Responda
-
\(y=-\frac{3}{4}+\frac{\sqrt{7}}{4}, y=-\frac{3}{4}-\frac{\sqrt{7}}{4}\)
Começaremos a solução para o próximo exemplo isolando o termo binomial.
Resolver:\(2(x-2)^{2}+3=57\).
Solução:
\(2(x-2)^{2}+3=57\)
Subtraia\(3\) de ambos os lados para isolar o termo binomial.
\(2(x-2)^{2}=54\)
Divida os dois lados por\(2\).
\((x-2)^{2}=27\)
Use a propriedade Square Root.
\(x-2=\pm \sqrt{27}\)
Simplifique o radical.
\(x-2=\pm 3 \sqrt{3}\)
Resolva para\(x\).
\(x=2 \pm 3 \sqrt{3}\)
Reescreva para mostrar duas soluções.
\(x=2+3 \sqrt{3}, x=2-3 \sqrt{3}\)
Confira:
Deixamos o cheque para você.
Resolver:\(5(a-5)^{2}+4=104\).
- Responda
-
\(a=5+2 \sqrt{5}, a=5-2 \sqrt{5}\)
Resolver:\(3(b+3)^{2}-8=88\).
- Responda
-
\(b=-3+4 \sqrt{2}, \quad b=-3-4 \sqrt{2}\)
Às vezes, as soluções são números complexos.
Resolver:\((2 x-3)^{2}=-12\).
Solução:
\((2 x-3)^{2}=-12\)
Use a propriedade Square Root.
\(2 x-3=\pm \sqrt{-12}\)
Simplifique o radical.
\(2 x-3=\pm 2 \sqrt{3} i\)
Adicione\(3\) aos dois lados.
\(2 x=3 \pm 2 \sqrt{3} i\)
Divida os dois lados por\(2\).
\(x=\frac{3 \pm 2 \sqrt{3 i}}{2}\)
Reescreva no formato padrão.
\(x=\frac{3}{2} \pm \frac{2 \sqrt{3} i}{2}\)
Simplifique.
\(x=\frac{3}{2} \pm \sqrt{3} i\)
Reescreva para mostrar duas soluções.
\(x=\frac{3}{2}+\sqrt{3} i, x=\frac{3}{2}-\sqrt{3} i\)
Confira:
Deixamos o cheque para você.
Resolver:\((3 r+4)^{2}=-8\).
- Responda
-
\(r=-\frac{4}{3}+\frac{2 \sqrt{2} i}{3}, r=-\frac{4}{3}-\frac{2 \sqrt{2} i}{3}\)
Resolver:\((2 t-8)^{2}=-10\).
- Responda
-
\(t=4+\frac{\sqrt{10} i}{2}, t=4-\frac{\sqrt{10 i}}{2}\)
Os lados esquerdos das equações nos próximos dois exemplos não parecem ter a forma\(a(x-h)^{2}\). Mas eles são trinômios quadrados perfeitos, então vamos levá-los em consideração para colocá-los na forma que precisamos.
Resolver:\(4 n^{2}+4 n+1=16\).
Solução:
Percebemos que o lado esquerdo da equação é um trinômio quadrado perfeito. Vamos considerar isso primeiro.
| \(4 n^{2}+4 n+1=16\) | |
| Considere o trinômio quadrado perfeito. | \((2 n+1)^{2}=16\) |
| Use a propriedade Square Root. | \(2 n+1=\pm \sqrt{16}\) |
| Simplifique o radical. | \(2 n+1=\pm 4\) |
| Resolva para\(n\). | \(2 n=-1 \pm 4\) |
| Divida cada lado por\(2\). | \(\begin{aligned} \frac{2 n}{2} &=\frac{-1 \pm 4}{2} \\ n &=\frac{-1 \pm 4}{2} \end{aligned}\) |
| Reescreva para mostrar duas soluções. | \(n=\frac{-1+4}{2}, n=\frac{-1-4}{2}\) |
| Simplifique cada equação. | \(n=\frac{3}{2}, \quad n=-\frac{5}{2}\) |
|
Confira: 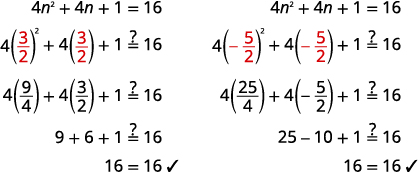
|
Resolver:\(9 m^{2}-12 m+4=25\).
- Responda
-
\(m=\frac{7}{3}, \quad m=-1\)
Resolver:\(16 n^{2}+40 n+25=4\).
- Responda
-
\(n=-\frac{3}{4}, \quad n=-\frac{7}{4}\)
Acesse este recurso on-line para obter instruções e práticas adicionais sobre o uso da propriedade de raiz quadrada para resolver equações quadráticas.
Conceitos-chave
- Propriedade de raiz quadrada
- Se\(x^{2}=k\), então\(x=\sqrt{k}\) ou\(x=-\sqrt{k}\) ou\(x=\pm \sqrt{k}\)
- Isole o termo quadrático e torne seu coeficiente um.
- Use a propriedade de raiz quadrada.
- Simplifique o radical.
- Verifique as soluções.


