Skip to main content
Global

7.6: Resolva aplicativos com equações racionais

  1. Last updated
  2. Save as PDF
  • Page ID
    183609

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de
    • Resolva proporções
    • Resolva aplicações de figuras semelhantes
    • Resolva aplicações de movimento uniforme
    • Resolva aplicativos de trabalho
    • Resolva problemas de variação direta
    • Resolva problemas de variação inversa
    Nota

    Antes de começar, faça este teste de prontidão.

    1. Exemplo 2.2.13. Exemplo 2.5.13. Exemplo 2.2.9.

    Resolva proporções

    Quando duas expressões racionais são iguais, a equação que as relaciona é chamada de proporção.

    Proporção

    Uma proporção é uma equação da forma\(\dfrac{a}{b}=\dfrac{c}{d}\), onde\(b \neq 0, d \neq 0\).

    A proporção é lida como “\(a\)é\(b\) como\(c\) está”\(d\).

    A equação\(\dfrac{1}{2}=\dfrac{4}{8}\) é uma proporção porque as duas frações são iguais. A proporção\(\dfrac{1}{2}=\dfrac{4}{8}\) é lida como “1 é para 2, assim como 4 é para 8”.

    Como uma proporção é uma equação com expressões racionais, resolveremos proporções da mesma forma que resolvemos equações racionais. Multiplicaremos os dois lados da equação pelo LCD para limpar as frações e, em seguida, resolver a equação resultante.

    Exemplo\(\PageIndex{1}\)

    Resolver:\(\dfrac{n}{n+14}=\dfrac{5}{7}\).

    Solução

    \[\dfrac{n}{n+14}=\dfrac{5}{7}, \quad n \neq-14 \nonumber \]

    Multiplique os dois lados pelo LCD.

    \[7(n+14)\left(\dfrac{n}{n+14}\right)=7(n+14)\left(\dfrac{5}{7}\right) \nonumber \]

    Remova os fatores comuns em cada lado.

    \[7 n=5(n+14) \nonumber \]

    Simplifique.

    \[7 n=5 n+70 \nonumber \]

    Resolva para\(n\).

    \[\begin{aligned} 2n&=70\\ n&=35 \end{aligned} \nonumber \]

    Confira.

    \[\dfrac{n}{n+14}=\dfrac{5}{7} \nonumber \]

    Substituto\(n=35\)

    \[\dfrac{35}{35+14} \overset{?}{=} \dfrac{5}{7} \nonumber \]

    Simplifique.

    \[\dfrac{35}{49} \overset{?}{=} \dfrac{5}{7} \nonumber \]

    Mostre fatores comuns.

    \[\dfrac{5 \cdot 7}{7 \cdot 7} \overset{?}{=} \dfrac{5}{7} \nonumber \]

    Simplifique.

    \[\dfrac{5}{7}=\dfrac{5}{7}\; \surd \nonumber \]

    Exercício\(\PageIndex{1}\)

    Resolva a proporção:\(\dfrac{y}{y+55}=\dfrac{3}{8}\).

    Resposta

    \(y=33\)

    Exercício\(\PageIndex{2}\)

    Resolva a proporção:\(\dfrac{z}{z-84}=-\dfrac{1}{5}\).

    Resposta

    \(z=14\)

    Observe no último exemplo que, quando eliminamos as frações multiplicando pelo LCD, o resultado é o mesmo que se tivéssemos multiplicado cruzadamente.

    \[\begin{aligned} \dfrac{n}{n+14}=\dfrac{5}{7} \quad \quad \quad \dfrac{n}{n+14}=\dfrac{5}{7} \\ 7(n+14)\left(\dfrac{n}{n+14}\right)=7(n+14)\left(\dfrac{5}{7}\right) \quad \quad \quad \dfrac{n}{n+14}=\dfrac{5}{7} \\ 7n=5(n+14) \quad \quad \quad 7n=5(n+14) \end{aligned} \nonumber \]

    Para qualquer proporção\(\dfrac{a}{b}=\dfrac{c}{d}\), obtemos o mesmo resultado quando eliminamos as frações multiplicando pelo LCD e quando multiplicamos cruzadamente.

    \[\begin{aligned} \dfrac{a}{b} =\dfrac{c}{d} \quad \quad \quad \dfrac{a}{b}=\dfrac{c}{d} \\ bd\left(\dfrac{a}{b}=\frac{c}{d}\right) bd \quad \quad \quad \frac{a}{b} = \frac{c}{d} \\ ad =bc \quad \quad \quad ad=bc \end{aligned} \nonumber \]

    Para resolver aplicações com proporções, seguiremos nossa estratégia usual para resolver aplicações. Mas quando configuramos a proporção, devemos ter certeza de que as unidades estão corretas: as unidades nos numeradores devem coincidir umas com as outras e as unidades nos denominadores também devem coincidir umas com as outras.

    Quando os pediatras prescrevem paracetamol para crianças, eles prescrevem 5 mililitros (ml) de acetaminofeno para cada 25 libras do peso da criança. Se Zoe pesar 80 libras, quantos mililitros de acetaminofeno seu médico prescreverá?

    Solução

    Identifique o que devemos encontrar e escolha uma variável para representá-lo.

    Quantos ml de acetaminofeno o médico prescreverá?

    Deixe\(a=ml\) de acetaminofeno.

    Escreva uma frase que forneça as informações para encontrá-la.

    Se 5 ml forem prescritos para cada 25 libras, quanto será prescrito para 80 libras?

    Traduza em uma proporção — tenha cuidado com as unidades.

    Etapa 1. Escreva a desigualdade como um quociente à esquerda e zero à direita. Nossa desigualdade está nessa forma.

    \[\dfrac{x-1}{x+3} \geq 0 \nonumber \]

    Etapa 2. Determine os pontos críticos - os pontos em que a expressão racional será zero ou indefinida.

    A expressão racional será zero quando o numerador for zero. Desde\(x-1=0\) quando\(x=1\), então 1 é um ponto crítico. A expressão racional será indefinida quando o denominador for zero. Desde\(x+3=0\) quando\(x=-3\), -3 é um ponto crítico.

    Etapa 3. Use os pontos críticos para dividir a reta numérica em intervalos.

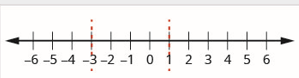
    clipboard_ee2fe708799269f0539168f8443a351d2.png

    Etapa 4. Acima da linha numérica, mostre o sinal de cada fator da expressão racional em cada intervalo. Abaixo da linha numérica, mostre o sinal do quociente.

    Use valores em cada intervalo para determinar o valor de cada fator no intervalo. No intervalo (-3,1), zero é um bom valor para testar. Por exemplo, quando\(x=0\) então\(x-1=-1\) e\(x+3=3\) O fator\(x-1\) é marcado como negativo e\(x+3\) marcado como positivo. Como um negativo dividido por um positivo é negativo, o quociente é marcado como negativo nesse intervalo.

    Etapa 5. Determine os intervalos em que a desigualdade está correta. Escreva a solução em notação de intervalo.

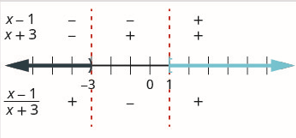
    clipboard_edae13eef9fc14a8139b8d2bcd44dd965.png

    Queremos que o quociente seja maior ou igual a zero, então os números nos intervalos\((-\infty,-3)\)\((1, \infty)\) são soluções. Como 3 deve ser excluído, pois torna a expressão racional 0, não podemos incluí-lo na solução. Podemos incluir 1 em nossa solução.

    \[(-\infty,-3) \cup[1, \infty) \nonumber \]

    Multiplique os dois lados pelo LCD, 400. Remova os fatores comuns em cada lado. Simplifique, mas não multiplique à esquerda. Observe qual será a próxima etapa.

    \[16 \cdot 5=5 a \nonumber \]

    Resolva para\(a\).

    \[\begin{aligned} \dfrac{16 \cdot 5}{5}&=\dfrac{5 a}{5}\\ 16&=a \end{aligned} \nonumber \]

    Confira. A resposta é razoável? Escreva uma frase completa.

    O pediatra prescreveria 16 ml de acetaminofeno para Zoe.

    Exercício\(\PageIndex{3}\)

    Os pediatras prescrevem 5 mililitros (ml) de acetaminofeno para cada 25 libras do peso de uma criança. Quantos mililitros de acetaminofeno o médico prescreverá para Emilia, que pesa 60 libras?

    Resposta

    O pediatra prescreverá 12 ml de acetaminofeno para Emilia.

    Exercício\(\PageIndex{4}\)

    Para cada 1 kg (kg) do peso de uma criança, os pediatras prescrevem 15 miligramas (mg) de um redutor de febre. Se Isabella pesar 12 kg, quantos miligramas do redutor de febre o pediatra prescreverá?

    Resposta

    O pediatra prescreverá 180 mg de redutor de febre para Isabella.

    Resolva aplicações de figuras semelhantes

    Quando você encolhe ou amplia uma foto em um telefone ou tablet, descobre uma distância em um mapa ou usa um padrão para construir uma estante de livros ou costurar um vestido, você está trabalhando com figuras semelhantes. Se duas figuras tiverem exatamente a mesma forma, mas tamanhos diferentes, elas são consideradas semelhantes. Um é um modelo em escala do outro. Todos os ângulos correspondentes têm as mesmas medidas e os lados correspondentes têm a mesma proporção.

    Figuras semelhantes

    Duas figuras são semelhantes se as medidas de seus ângulos correspondentes forem iguais e seus lados correspondentes tiverem a mesma proporção.

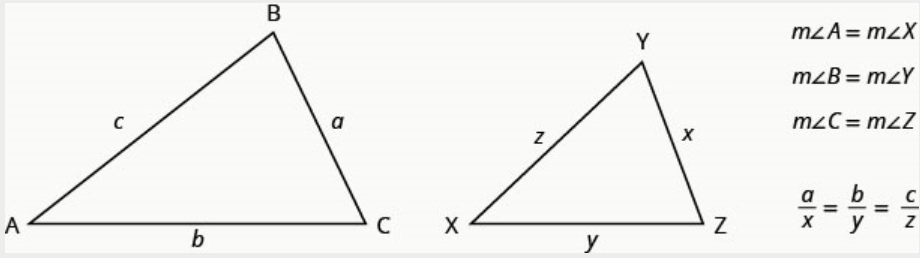
    Por exemplo, os dois triângulos na Figura abaixo são semelhantes. Cada lado de \(\Delta ABC\)tem quatro vezes o comprimento do lado correspondente de \(\Delta XYZ\).

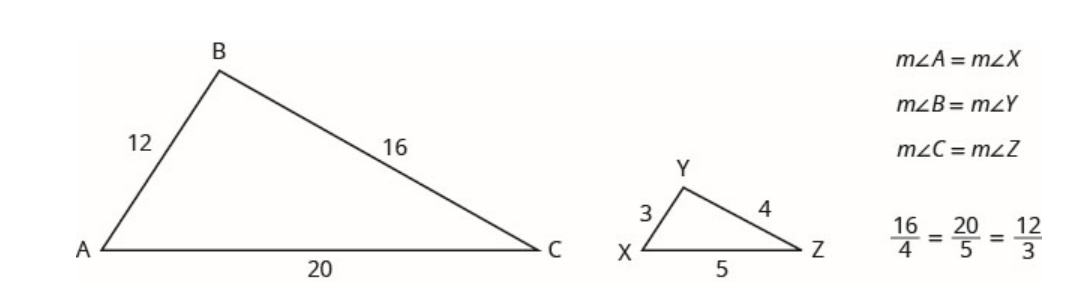
    clipboard_e856a7de8b3a79dcd08723d9871ccd270.png

    Isso é resumido na Propriedade de Triângulos Similares.

    Propriedade de triângulos similares

    Se\(\Delta ABC\) for semelhante a\(\Delta XYZ\), então sua medida angular correspondente é igual e seus lados correspondentes têm a mesma proporção.

    clipboard_e4fdc3b30588979c50d44a48aef0d74a0.png

    Para resolver aplicativos com números semelhantes, seguiremos a Estratégia de Solução de Problemas para Aplicações Geométricas que usamos anteriormente.

    Exemplo\(\PageIndex{3}\)

    Em um mapa, São Francisco, Las Vegas e Los Angeles formam um triângulo. A distância entre as cidades é medida em polegadas. A figura à esquerda abaixo representa o triângulo formado pelas cidades no mapa. Se a distância real de Los Angeles a Las Vegas for 270 milhas, encontre a distância de Los Angeles a São Francisco.

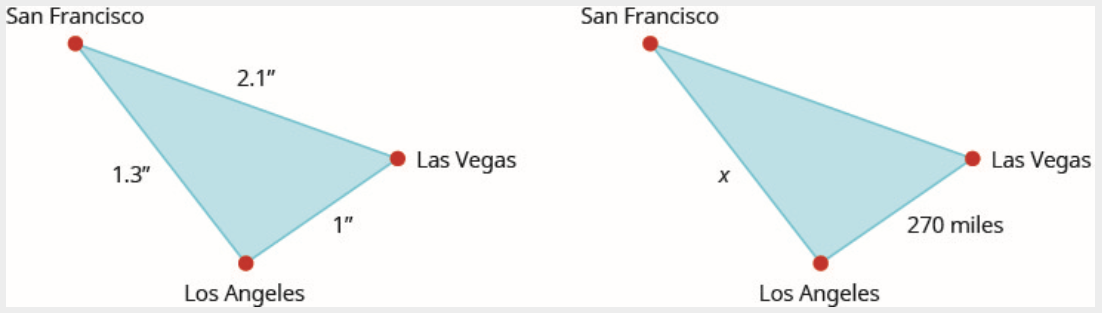
    clipboard_efb0263e1d94381d6b9257775d879ded0.png

    Solução

    Como os triângulos são semelhantes, os lados correspondentes são proporcionais.

    Leia o problema. Desenhe as figuras e identifique-as com as informações fornecidas. Os números são mostrados acima.

    Identifique o que estamos procurando: a distância real de Los Angeles a São Francisco

    Nomeie as variáveis: Let\(x\) = distância de Los Angeles a São Francisco.

    Traduza em uma equação. Como os triângulos são semelhantes, os lados correspondentes são proporcionais. Faremos os numeradores “milhas” e os denominadores “polegadas”.

    \[$\dfrac{x \text { miles }}{1.3 \text { inches }}=\dfrac{270 \text { miles }}{1 \text { inch }}$ \nonumber \]

    Resolva a equação.

    \[\begin{aligned} 1.3\left(\dfrac{x}{1.3}\right)&=1.3\left(\dfrac{270}{1}\right) \\ x&=351 \end{aligned} \nonumber \]

    Confira. No mapa, a distância de Los Angeles a São Francisco é maior do que a distância de Los Angeles a Las Vegas. Como 351 é mais de 270, a resposta faz sentido.

    Verifique\(x=351\) a proporção original. Use uma calculadora.

    \[\begin {aligned} \dfrac{x \text { miles }}{1.3 \text { inches }}&=\dfrac{270 \text { miles }}{1 \text { inch }}\\ \dfrac{351 \text { miles }}{1.3 \text { inches }} &\overset{?}{=} \dfrac{270 \text { miles }}{1 \text { inch }}\\ \dfrac{270 \text { miles }}{1 \text { inch }}&=\dfrac{270 \text { miles }}{1 \text { inch }} \surd \end{aligned} \nonumber \]

    Responda à pergunta: A distância de Los Angeles a São Francisco é de 351 milhas.

    No mapa, Seattle, Portland e Boise formam um triângulo. A distância entre as cidades é medida em polegadas. A figura à esquerda abaixo representa o triângulo formado pelas cidades no mapa. A distância real de Seattle a Boise é de 400 milhas.

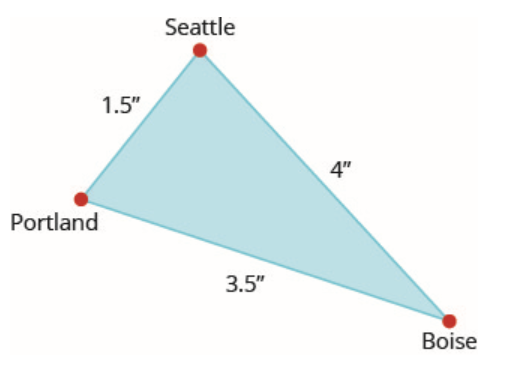
    clipboard_e545a49106f741f6a3b36f53e39ed4458.png

    Exercício\(\PageIndex{5}\)

    Encontre a distância real de Seattle a Portland.

    Resposta

    A distância é de 150 milhas.

    Exercício\(\PageIndex{6}\)

    Encontre a distância real de Portland a Boise.

    Resposta

    A distância é de 350 milhas.

    Podemos usar números semelhantes para encontrar alturas que não podemos medir diretamente.

    Exemplo\(\PageIndex{4}\)

    Tyler tem 6 pés de altura. No final de uma tarde, sua sombra tinha 8 pés de comprimento. Ao mesmo tempo, a sombra de uma árvore tinha 24 pés de comprimento. Encontre a altura da árvore.

    Solução

    Leia o problema e desenhe uma figura. Estamos procurando\(h\) a altura da árvore.

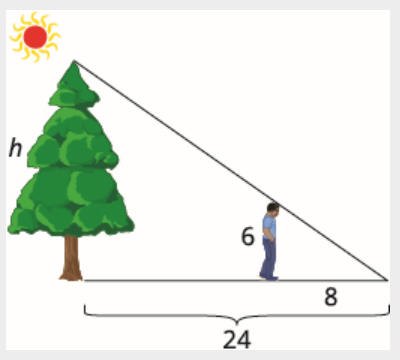
    clipboard_ee900ec650dd61d33cbc8b7d340874f27.png

    Usaremos triângulos semelhantes para escrever uma equação. O pequeno triângulo é semelhante ao triângulo grande.

    \[\dfrac{h}{24}=\dfrac{6}{8} \nonumber \]

    Resolva a proporção.

    \[\begin {aligned} 24\left(\dfrac{6}{8}\right)&=24\left(\dfrac{h}{24}\right)\\ 18&=h \end{aligned} \nonumber \]

    Simplifique. Confira.

    A altura de Tyler é menor que o comprimento de sua sombra, então faz sentido que a altura da árvore seja menor que o comprimento de sua sombra. Verifique\(h=18\) a proporção original.

    \[\begin{aligned} &\dfrac{6}{8}=\dfrac{h}{24}\\ &\dfrac{6}{8} \overset{?}{=} \dfrac{18}{24}\\ &\dfrac{3}{4}=\dfrac{3}{4} \surd \end{aligned} \nonumber \]

    Exercício\(\PageIndex{7}\)

    Um poste telefônico projeta uma sombra de 50 pés de comprimento. Perto dali, um sinal de trânsito de 8 pés de altura projeta uma sombra de 10 pés de comprimento. Qual é a altura do poste telefônico?

    Resposta

    O poste telefônico tem 40 pés de altura.

    Exercício\(\PageIndex{8}\)

    Um pinheiro projeta uma sombra de 80 pés ao lado de um prédio de 30 pés de altura que projeta uma sombra de 40 pés. Qual é a altura do pinheiro?

    Resposta

    O pinheiro tem 60 pés de altura.

    Resolva aplicações de movimento uniforme

    Resolvemos problemas de movimento uniforme usando a fórmula\(D=r t\) dos capítulos anteriores. Usamos uma tabela como a abaixo para organizar as informações e nos levar à equação.

    \(\cdot\)Tempo de taxa = Distância
      \ (\ cdot\) Tempo = Distância” class="lt-math-14671">    
      \ (\ cdot\) Tempo = Distância” class="lt-math-14671">    

    A fórmula\(D=r t\) pressupõe que nós os conhecemos\(r\)\(t\) e os usamos para encontrar\(D\). Se soubéssemos\(D\)\(r\) e precisássemos encontrar\(t\), resolveríamos a equação\(t\) e obteríamos a fórmula\(t=\dfrac{D}{r}\).

    Também explicamos como voar com ou contra o vento afeta a velocidade de um avião. Vamos revisitar essa ideia no próximo exemplo.

    Exemplo\(\PageIndex{5}\)

    Um avião pode voar 200 milhas em um vento contrário de 30 mph na mesma quantidade de tempo que leva para voar 300 milhas com um vento de cauda de 30 mph. Qual é a velocidade do avião?

    Solução

    Esta é uma situação de movimento uniforme. Um diagrama nos ajudará a visualizar a situação.

    clipboard_e675478d490b6955418a9d40f7346c6b5.png

    Preenchemos o gráfico para organizar as informações.

    Estamos procurando a velocidade do avião. Seja\(r\) = a velocidade do avião.

    Quando o avião voa com o vento, o vento aumenta sua velocidade e, portanto, a taxa aumenta\(r + 30\).

    Quando o avião voa contra o vento, o vento diminui sua velocidade e a taxa é\(r − 30\).

    Escreva nas tarifas. Escreva à distância. Desde então\(D=r \cdot t\), resolvemos\(t\) e obtemos\(t=\dfrac{D}{r}\). Dividimos a distância pela taxa em cada linha e colocamos a expressão na coluna de tempo.

    \(\cdot\)Tempo de taxa = Distância
    Vento contrário \ (\ cdot\) Tempo = Distância">\(r-30\) \(\dfrac{200}{r-30}\) 200
    vento de cauda \ (\ cdot\) Tempo = Distância">\(r+30\) \(\dfrac{300}{r+30}\) 300

    Sabemos que os tempos são iguais e, por isso, escrevemos nossa equação.

    \[\dfrac{200}{r-30}=\dfrac{300}{r+30} \nonumber \]

    Multiplicamos os dois lados pelo LCD.

    \[(r+30)(r-30)\left(\frac{200}{r-30}\right)=(r+30)(r-30)\left(\frac{300}{r+30}\right) \nonumber \]

    Simplifique e resolva.

    \[\begin{aligned} (r+30)(200)&=(r-30) 300 \\ 200 r+6000&=300 r-9000 \\ 15000&=100 r \end{aligned} \nonumber \]

    Confira.

    É\(150 \mathrm{mph}\) uma velocidade razoável para um avião? Sim. Se o avião estiver viajando\(150 \mathrm{mph}\) e o vento estiver\(30 \mathrm{mph}\),

    \[\text { Tailwind } \quad 150+30=180 \mathrm{mph} \quad \dfrac{300}{180}=\dfrac{5}{3} \text { hours } \nonumber \]

    \[\text { Headwind } 150-30=120 \mathrm{mph} \dfrac{200}{120}=\dfrac{5}{3} \text { hours } \nonumber \]

    Os tempos são iguais, então verifica. O avião estava viajando\(150 \mathrm{mph}\).

    Exercício\(\PageIndex{9}\)

    Link pode andar de bicicleta 20 milhas em um vento contrário de 3 mph na mesma quantidade de tempo que ele pode andar 30 milhas com um vento de cauda de 3 mph. Qual é a velocidade de ciclismo do Link?

    Responda

    A velocidade de bicicleta de Link é de 15 mph.

    Exercício\(\PageIndex{10}\)

    Danica pode navegar em seu barco 5 milhas em um vento contrário de 7 mph na mesma quantidade de tempo que ela pode navegar 12 milhas com um vento de cauda de 7 mph. Qual é a velocidade do barco de Danica sem vento?

    Responda

    A velocidade do barco de Danica é de 17 mph.

    No próximo exemplo, saberemos o tempo total resultante de percorrer distâncias diferentes em velocidades diferentes.

    Exemplo\(\PageIndex{6}\)

    Jazmine treinou por 3 horas no sábado. Ela correu 8 milhas e depois pedalou 24 milhas. Sua velocidade de ciclismo é 4 mph mais rápida do que sua velocidade de corrida. Qual é a velocidade de corrida dela?

    Solução

    Esta é uma situação de movimento uniforme. Um diagrama nos ajudará a visualizar a situação.

    clipboard_ea415f63ad2acc69c7ea17326f1ee0337.png

    Preenchemos o gráfico para organizar as informações. Estamos procurando a velocidade de corrida de Jazmine. Let\(r\) = velocidade de corrida de Jazmine.

    Sua velocidade de bicicleta é 4 milhas mais rápida do que sua velocidade de corrida. \(r + 4\)= sua velocidade de ciclismo

    As distâncias são dadas, insira-as no gráfico. Desde então\(D=r \cdot t\), resolvemos\(t\) e obtemos\(t=\dfrac{D}{r}\). Dividimos a distância pela taxa em cada linha e colocamos a expressão na coluna de tempo.

    \(\cdot\)Tempo de taxa = Distância
    Corra \ (\ cdot\) Tempo = Distância">\(r\) \(\dfrac{8}{r}\) 8
    Bicicleta \ (\ cdot\) Tempo = Distância">\(r+4\) \(\dfrac{24}{r+4}\) 24
      \ (\ cdot\) Tempo = Distância"> 3  

    Escreva uma frase de palavras: O tempo dela mais o tempo de bicicleta é de 3 horas.

    Traduza a frase para obter a equação.

    \[\dfrac{8}{r}+\dfrac{24}{r+4}=3 \nonumber \]

    Resolver.

    \ [\ begin {alinhado}
    r (r+4)\ esquerda (\ dfrac {8} {r} +\ dfrac {24} {r+4}\ direita) &=3\ cdot r (r+4)\\
    8 (r+4) +24 r &=3 r (r+4)\
    8 r+32+24 r &=3 r^ {2} +12 r\\
    32+32 r &=3 r^ {2} +12 r\\
    0 &=3 r^ {2} -20 r-32\\
    0 & =( 3 r+ 4) (r-8)
    \ end {alinhado}\ nonumber\]

    \[\begin{array}{lc} {(3 r+4)=0} & {(r-8)=0} \\ \cancel{r=\dfrac{4}{3}} \quad & {r=8} \end{array} \nonumber \]

    Verifique.

    Uma velocidade negativa não faz sentido nesse problema, assim como\(r=8\) a solução.

    8 mph é uma velocidade de corrida razoável? Sim.

    Se a taxa de corrida de Jazmine for 4, então sua taxa de ciclismo\(r+4\),, qual é\(8+4=12\).

    \[\text { Run } 8 \mathrm{mph} \quad \dfrac{8 \mathrm{miles}}{8 \mathrm{mph}}=1 \text { hour } \nonumber \]

    \[\text { Bike } 12 \text { mph } \quad \dfrac{24 \text { miles }}{12 \mathrm{mph}}=2 \text { hours } \nonumber \]

    \(y=\dfrac{k}{x}\)