7.3: Adicionar e subtrair expressões racionais
- Page ID
- 183640
Ao final desta seção, você poderá:
- Adicione e subtraia expressões racionais com um denominador comum
- Adicione e subtraia expressões racionais cujos denominadores são opostos
- Encontre o denominador menos comum de expressões racionais
- Adicione e subtraia expressões racionais com denominadores diferentes
- Adicione e subtraia funções racionais
Adicione e subtraia expressões racionais com um denominador comum
Qual é o primeiro passo que você dá ao adicionar frações numéricas? Você verifica se eles têm um denominador comum. Se o fizerem, você adiciona os numeradores e coloca a soma sobre o denominador comum. Se eles não tiverem um denominador comum, você encontrará um antes de adicionar.
É o mesmo com expressões racionais. Para adicionar expressões racionais, elas devem ter um denominador comum. Quando os denominadores são iguais, você adiciona os numeradores e coloca a soma sobre o denominador comum.
Se\(p\)\(q\), e\(r\) são polinômios onde\(r\neq 0\), então
\[\dfrac{p}{r}+\dfrac{q}{r}=\dfrac{p+q}{r} \quad \text{and} \quad \dfrac{p}{r}−\dfrac{q}{r}=\dfrac{p−q}{r}\nonumber\]
Para adicionar ou subtrair expressões racionais com um denominador comum, adicione ou subtraia os numeradores e coloque o resultado sobre o denominador comum.
Sempre simplificamos as expressões racionais. Certifique-se de fatorar, se possível, depois de subtrair os numeradores para poder identificar quaisquer fatores comuns.
Lembre-se também de que não permitimos valores que tornariam o denominador zero. Qual valor de\(x\) deve ser excluído no próximo exemplo?
Adicionar:\(\dfrac{11x+28}{x+4}+\dfrac{x^2}{x+4}\).
Solução
Como o denominador é\(x+4\), devemos excluir o valor\(x=−4\).
\(\begin{array} {ll} &\dfrac{11x+28}{x+4}+\dfrac{x^2}{x+4},\space x\neq −4 \\ \begin{array} {l} \text{The fractions have a common denominator,} \\ \text{so add the numerators and place the sum} \\ \text{over the common denominator.} \end{array} &\dfrac{11x+28+x^2}{x+4} \\ & \\ \text{Write the degrees in descending order.} &\dfrac{x^2+11x+28}{x+4} \\ & \\ \text{Factor the numerator.} &\dfrac{(x+4)(x+7)}{x+4} \\ & \\ \text{Simplify by removing common factors.} &\dfrac{\cancel{(x+4)}(x+7)}{\cancel{x+4}} \\ & \\ \text{Simplify.} &x+7 \end{array}\)
A expressão simplifica para\(x+7\), mas a expressão original tinha um denominador de\(x+4\) sim\(x\neq −4\).
Simplifique:\(\dfrac{9x+14}{x+7}+\dfrac{x^2}{x+7}\).
- Responda
-
\(x+2\)
Simplifique:\(\dfrac{x^2+8x}{x+5}+\dfrac{15}{x+5}\).
- Responda
-
\(x+3\)
Para subtrair expressões racionais, elas também devem ter um denominador comum. Quando os denominadores são iguais, você subtrai os numeradores e coloca a diferença sobre o denominador comum. Tenha cuidado com os sinais ao subtrair um binômio ou trinômio.
Subtraia:\(\dfrac{5x^2−7x+3}{x^2−3x+18}−\dfrac{4x^2+x−9}{x^2−3x+18}\).
Solução
\(\begin{array} {ll} &\dfrac{5x^2−7x+3}{x^2−3x+18}−\dfrac{4x^2+x−9}{x^2−3x+18} \\ & \\ \begin{array} {l} \text{Subtract the numerators and place the} \\ \text{difference over the common denominator.} \end{array} &\dfrac{5x^2−7x+3−(4x^2+x−9)}{x^2−3x+18} \\ & \\ \text{Distribute the sign in the numerator.} &\dfrac{5x^2−7x+3−4x^2−x+9}{x^2−3x−18} \\ & \\ \text{Combine like terms.} &\dfrac{x^2−8x+12}{x^2−3x−18} \\ & \\ \text{Factor the numerator and the denominator.} &\dfrac{(x−2)(x−6)}{(x+3)(x−6)} \\ & \\ \text{Simplify by removing common factors.} &\dfrac{(x−2)\cancel{(x−6)}}{(x+3)\cancel{(x−6)}} \\ & \\ &(x−2)(x+3) \end{array}\)
Subtraia:\(\dfrac{4x^2−11x+8}{x^2−3x+2}−\dfrac{3x^2+x−3}{x^2−3x+2}\).
- Responda
-
\(\dfrac{x−11}{x−2}\)
Subtraia:\(\dfrac{6x^2−x+20}{x^2−81}−\dfrac{5x^2+11x−7}{x^2−81}\).
- Responda
-
\(\dfrac{x−3}{x+9}\)
Adicione e subtraia expressões racionais cujos denominadores são opostos
Quando os denominadores de duas expressões racionais são opostos, é fácil obter um denominador comum. Só temos que multiplicar uma das frações por\(\dfrac{−1}{−1}\).
Vamos ver como isso funciona.
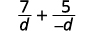 |
|
| Multiplique a segunda fração por\(\dfrac{−1}{−1}\). | 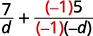 |
| Os denominadores são os mesmos. | 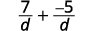 |
| Simplifique. | 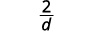 |
Tenha cuidado com os sinais ao trabalhar com os opostos quando as frações estão sendo subtraídas.
Subtraia:\(\dfrac{m^2−6m}{m^2−1}−\dfrac{3m+2}{1−m^2}\).
Solução
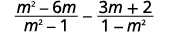 |
|
|
Os denominadores são opostos, então multiplique a |
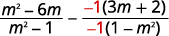 |
| Simplifique a segunda fração. | 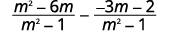 |
| Os denominadores são os mesmos. Subtraia os numeradores. | 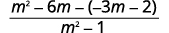 |
| Distribuir. | 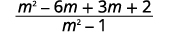 |
| Combine termos semelhantes. | 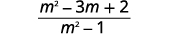 |
| Fator o numerador e o denominador. | 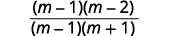 |
| Simplifique removendo fatores comuns. | 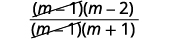 |
| Simplifique. | 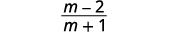 |
Subtraia:\(\dfrac{y^2−5y}{y^2−4}−\dfrac{6y−6}{4−y^2}\).
- Responda
-
\(\dfrac{y+3}{y+2}\)
Subtraia:\(\dfrac{2n^2+8n−1}{n^2−1}−\dfrac{n^2−7n−1}{1−n^2}\).
- Responda
-
\(\dfrac{3n−2}{n−1}\)
Encontre o denominador menos comum de expressões racionais
Quando adicionamos ou subtraímos expressões racionais com denominadores diferentes, precisaremos obter denominadores comuns. Se revisarmos o procedimento que usamos com frações numéricas, saberemos o que fazer com expressões racionais.
Vejamos este exemplo:\(\dfrac{7}{12}+\dfrac{5}{18}\). Como os denominadores não são os mesmos, o primeiro passo foi encontrar o denominador menos comum (LCD).
Para encontrar o LCD das frações, fatoramos 12 e 18 em números primos, alinhando quaisquer números primos comuns em colunas. Em seguida, “derrubamos” um primo de cada coluna. Finalmente, multiplicamos os fatores para encontrar o LCD.
Quando adicionamos frações numéricas, uma vez que encontramos o LCD, reescrevemos cada fração como uma fração equivalente ao LCD multiplicando o numerador e o denominador pelo mesmo número. Agora estamos prontos para adicionar.
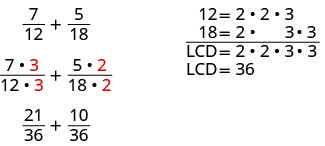
Fazemos a mesma coisa com expressões racionais. No entanto, deixamos o LCD na forma fatorada.
- Fatore cada denominador completamente.
- Liste os fatores de cada denominador. Combine os fatores verticalmente quando possível.
- Reduza as colunas incluindo todos os fatores, mas não inclua fatores comuns duas vezes.
- Escreva o LCD como o produto dos fatores.
Lembre-se de que sempre excluímos valores que tornariam o denominador zero. Quais valores de xx devemos excluir no próximo exemplo?
a. Encontre o LCD para as expressões\(\dfrac{8}{x^2−2x−3}\)\(\dfrac{3x}{x^2+4x+3}\) e b. reescreva-as como expressões racionais equivalentes com o menor denominador comum.
Solução
uma.
| Encontre o LCD para\(\dfrac{8}{x^2−2x−3}\),\(\dfrac{3x}{x^2+4x+3}\). | |
| Considere cada denominador completamente, alinhando fatores comuns. Derrube as colunas. |
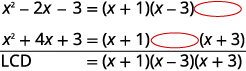 |
| Escreva o LCD como o produto dos fatores. | 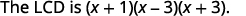 |
b.
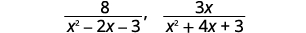 |
|
| Fatize cada denominador. | 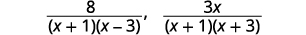 |
| Multiplique cada denominador pelo fator LCD “ausente” e multiplique cada numerador pelo mesmo fator. |
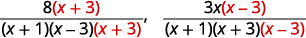 |
| Simplifique os numeradores. | 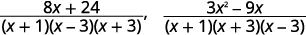 |
a. Encontre o LCD para as expressões\(\dfrac{2}{x^2−x−12}\),\(\dfrac{1}{x^2−16}\) b. reescreva-as como expressões racionais equivalentes com o menor denominador comum.
- Responda
-
a.\((x−4)(x+3)(x+4)\)
b.\(\dfrac{2x+8}{(x−4)(x+3)(x+4)}\),
\(\dfrac{x+3}{(x−4)(x+3)(x+4)}\)
a. Encontre o LCD para as expressões\(\dfrac{3x}{x^2−3x+10}\),\(\dfrac{5}{x^2+3x+2}\) b. reescreva-as como expressões racionais equivalentes com o menor denominador comum.
- Responda
-
a.\((x+2)(x−5)(x+1)\)
b.\(\dfrac{3x^2+3x}{(x+2)(x−5)(x+1)}\),
\(\dfrac{5x−25}{(x+2)(x−5)(x+1)}\)
Adicione e subtraia expressões racionais com denominadores diferentes
Agora temos todas as etapas necessárias para adicionar ou subtrair expressões racionais com denominadores diferentes.
Adicionar:\(\dfrac{3}{x−3}+\dfrac{2}{x−2}\).
Solução



Adicionar:\(\dfrac{2}{x−2}+\dfrac{5}{x+3}\).
- Responda
-
\(\dfrac{7x−4}{(x−2)(x+3)}\)
Adicionar:\(\dfrac{4}{m+3}+\dfrac{3}{m+4}\).
- Responda
-
\(\dfrac{7m+25}{(m+3)(m+4)}\)
As etapas usadas para adicionar expressões racionais estão resumidas aqui.
- Determine se as expressões têm um denominador comum.
- Sim — vá para a etapa 2.
- Não — Reescreva cada expressão racional com o LCD.
- Encontre o LCD.
- Reescreva cada expressão racional como uma expressão racional equivalente com o LCD.
- Adicione ou subtraia as expressões racionais.
- Simplifique, se possível.
Evite a tentação de simplificar muito cedo. No exemplo acima, devemos deixar a primeira expressão racional\(\dfrac{3x−6}{(x−3)(x−2)}\) para poder adicioná-la\(\dfrac{2x−6}{(x−2)(x−3)}\). Simplifique somente depois de combinar os numeradores.
Adicionar:\(\dfrac{8}{x^2−2x−3}+\dfrac{3x}{x^2+4x+3}\).
Solução
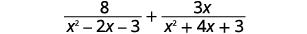 |
|
| As expressões têm um denominador comum? | Não. |
| Reescreva cada expressão com o LCD. | |
| \(\begin{array} {ll} & \\ & \\ \text{Find the LCD.} &\begin{array} {l} \hspace{5mm} x^2−2x−3=(x+1)(x−3) \\ \underline{x^2+4x+3=(x+1)\quad (x+3)} \\ & \\ \qquad LCD=(x+1)(x−3)(x+3) \end{array} \end{array} \) | |
| Reescreva cada expressão racional como uma expressão racional equivalente com o LCD. |
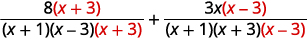 |
| Simplifique os numeradores. | 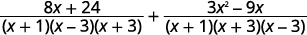 |
| Adicione as expressões racionais. | 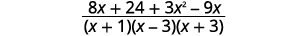 |
| Simplifique o numerador. | 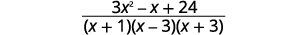 |
| O numerador é primo, então não há fatores comuns. |
Adicionar:\(\dfrac{1}{m^2−m−2}+\dfrac{5m}{m^2+3m+2}\).
- Responda
-
\(\dfrac{5m^2−9m+2}{(m+1)(m−2)(m+2)}\)
Adicionar:\(\dfrac{2n}{n^2−3n−10}+\dfrac{6}{n^2+5n+6}\).
- Responda
-
\(\dfrac{2n^2+12n−30}{(n+2)(n−5)(n+3)}\)
O processo que usamos para subtrair expressões racionais com denominadores diferentes é o mesmo da adição. Só precisamos ter muito cuidado com os sinais ao subtrair os numeradores.
Subtraia:\(\dfrac{8y}{y^2−16}−\dfrac{4}{y−4}\).
Solução
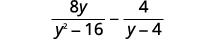 |
|
| As expressões têm um denominador comum? | Não. |
| Reescreva cada expressão com o LCD. | |
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} y^2−16=(y−4)(y+4) \\ \quad \underline{y−4=y−4} \\ LCD=(y−4)(y+4) \end{array} \end{array} \) | |
| Reescreva cada expressão racional como uma expressão racional equivalente com o LCD. |
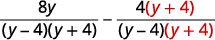 |
| Simplifique os numeradores. | 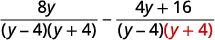 |
| Subtraia as expressões racionais. | 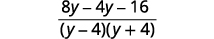 |
| Simplifique o numerador. | 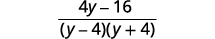 |
| Fator o numerador para procurar fatores comuns. | 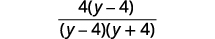 |
| Remova fatores comuns | 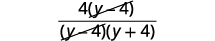 |
| Simplifique. | 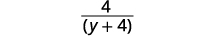 |
Subtraia:\(\dfrac{2x}{x^2−4}−\dfrac{1}{x+2}\).
- Responda
-
\(\dfrac{1}{x−2}\)
Subtraia:\(\dfrac{3}{z+3}−\dfrac{6z}{z^2−9}\).
- Responda
-
\(\dfrac{−3}{z−3}\)
Há muitos sinais negativos no próximo exemplo. Seja extremamente cuidadoso.
Subtraia:\(\dfrac{−3n−9}{n^2+n−6}−\dfrac{n+3}{2−n}\).
Solução
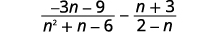 |
|
| Fator o denominador. | 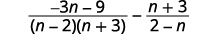 |
| Como\(n−2\) e\(2−n\) somos opostos, multiplicaremos a segunda expressão racional por\(\dfrac{−1}{−1}\). |
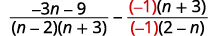 |
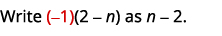 |
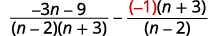 |
| Simplifique. Lembre-se,\(a−(−b)=a+b\). | 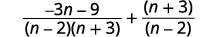 |
| As expressões racionais têm um denominador comum? Não. |
|
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} n^2+n−6=(n−2)(n+3) \\ \quad\underline{n−2=(n−2)} \\ LCD=\quad (n−2)(n+3) \end{array} \end{array} \) | |
| Reescreva cada expressão racional como uma expressão racional equivalente com o LCD. |
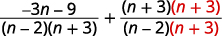 |
| Simplifique os numeradores. | 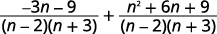 |
| Adicione as expressões racionais. | 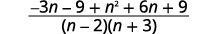 |
| Simplifique o numerador. | 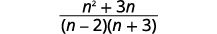 |
| Fator o numerador para procurar fatores comuns. | 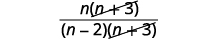 |
| Simplifique. | 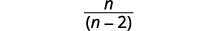 |
Subtraia:\(\dfrac{3x−1}{x^2−5x−6}−\dfrac{2}{6−x}\).
- Responda
-
\(\dfrac{5x+1}{(x−6)(x+1)}\)
Subtraia:\(\dfrac{−2y−2}{y^2+2y−8}−\dfrac{y−1}{2−y}\).
- Responda
-
\(\dfrac{y+3}{y+4}\)
As coisas podem ficar muito confusas quando as duas frações precisam ser multiplicadas por um binômio para obter o denominador comum.
Subtraia:\(\dfrac{4}{a^2+6a+5}−\dfrac{3}{a^2+7a+10}\).
Solução
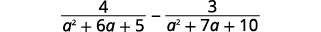 |
|
| Fatize os denominadores. | 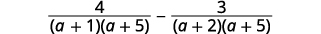 |
| As expressões racionais têm um denominador comum? Não. |
|
|
\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} a^2+6a+5=(a+1)(a+5) \\ \underline{a^2+7a+10=(a+5)(a+2)} \\ LCD=(a+1)(a+5)(a+2) \end{array} \end{array} \) |
|
| Reescreva cada expressão racional como uma expressão racional equivalente com o LCD. |
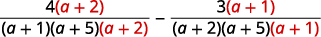 |
| Simplifique os numeradores. | 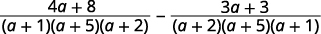 |
| Subtraia as expressões racionais. | 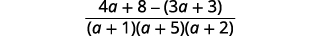 |
| Simplifique o numerador. | 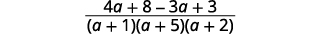 |
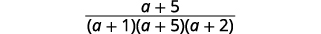 |
|
| Procure fatores comuns. | 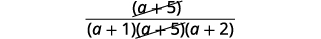 |
| Simplifique. | 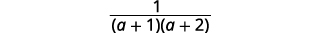 |
Subtraia:\(\dfrac{3}{b^2−4b−5}−\dfrac{2}{b^2−6b+5}\).
- Resposta
-
\(\dfrac{1}{(b+1)(b−1)}\)
Subtraia:\(\dfrac{4}{x^2−4}−\dfrac{3}{x^2−x−2}\).
- Resposta
-
\(\dfrac{1}{(x+2)(x+1)}\)
Seguimos os mesmos passos de antes para encontrar o LCD quando temos mais de duas expressões racionais. No próximo exemplo, começaremos fatorando todos os três denominadores para encontrar seu LCD.
Simplifique:\(\dfrac{2u}{u−1}+\dfrac{1}{u}−\dfrac{2u−1}{u^2−u}\).
Solução
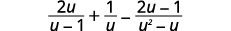 |
|
| As expressões têm um denominador comum? Não. Reescreva cada expressão com o LCD. |
|
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} u−1=(u−1) \\ u=u \\ \underline{u^2−u=u(u−1)} \\ LCD=u(u−1) \end{array} \end{array}\) | |
| Reescreva cada expressão racional como uma expressão racional equivalente com o LCD. |
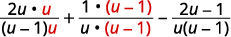 |
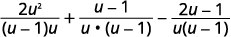 |
|
| Escreva como uma expressão racional. | 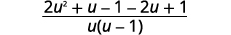 |
| Simplifique. | 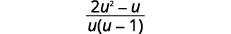 |
| Fatore o numerador e remova os fatores comuns. |
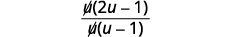 |
| Simplifique. | 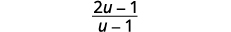 |
Simplifique:\(\dfrac{v}{v+1}+\dfrac{3}{v−1}−\dfrac{6}{v^2−1}\).
- Resposta
-
\(\dfrac{v+3}{v+1}\)
Simplifique:\(\dfrac{3w}{w+2}+\dfrac{2}{w+7}−\dfrac{17w+4}{w^2+9w+14}\).
- Resposta
-
\(\dfrac{3w}{w+7}\)
Adicione e subtraia funções racionais
Para adicionar ou subtrair funções racionais, usamos as mesmas técnicas que usamos para adicionar ou subtrair funções polinomiais.
Descubra\(R(x)=f(x)−g(x)\) onde\(f(x)=\dfrac{x+5}{x−2}\)\(g(x)=\dfrac{5x+18}{x^2−4}\) e.
- solução
-

Substitua nas funções\(f(x)\),\(g(x)\). 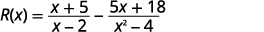
Fatize os denominadores. 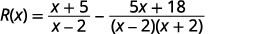
As expressões têm um denominador comum? Não.
Reescreva cada expressão com o LCD.\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} x−2=(x−2) \\ \underline{x^2−4=(x−2)(x+2)} \\ \hspace{4mm} LCD=(x−2)(x+2)\end{array} \end{array}\) Reescreva cada expressão racional como uma expressão racional
equivalente com o LCD.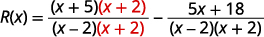
Escreva como uma expressão racional. 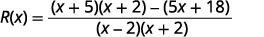
Simplifique. 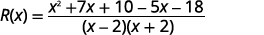
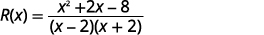
Fatore o numerador e remova os fatores
comuns.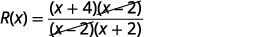
Simplifique. 
Descubra\(R(x)=f(x)−g(x)\) onde\(f(x)=\dfrac{x+1}{x+3}\)\(g(x)=\dfrac{x+17}{x^2−x−12}\) e.
- Resposta
-
\(\dfrac{x−7}{x−4}\)
Descubra\(R(x)=f(x)+g(x)\) onde\(f(x)=\dfrac{x−4}{x+3}\)\(g(x)=\dfrac{4x+6}{x^2−9}\) e.
- Resposta
-
\(\dfrac{x^2−3x+18}{(x+3)(x−3)}\)
Acesse esse recurso on-line para obter instruções e práticas adicionais sobre adição e subtração de expressões racionais.
- Adicione e subtraia expressões racionais - diferentemente dos denominadores
Conceitos-chave
- Adição e subtração de expressões racionais
Se\(p\)\(q\),, e\(r\) são polinômios onde\(r\neq 0\), então
\[\dfrac{p}{r}+\dfrac{q}{r}=\dfrac{p+q}{r} \quad \text{and} \quad \dfrac{p}{r}−\dfrac{q}{r}=\dfrac{p−q}{r}\nonumber\] - Como encontrar o denominador menos comum de expressões racionais.
- Considere cada expressão completamente.
- Liste os fatores de cada expressão. Combine os fatores verticalmente quando possível.
- Derrube as colunas.
- Escreva o LCD como o produto dos fatores.
- Como adicionar ou subtrair expressões racionais.
- Determine se as expressões têm um denominador comum.
- Sim — vá para a etapa 2.
- Não — Reescreva cada expressão racional com o LCD.
- Encontre o LCD.
- Reescreva cada expressão racional como uma expressão racional equivalente com o LCD.
- Adicione ou subtraia as expressões racionais.
- Simplifique, se possível.
- Determine se as expressões têm um denominador comum.


