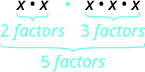5.3: Propriedades dos expoentes e notação científica
- Page ID
- 183239
Ao final desta seção, você poderá:
- Simplifique as expressões usando as propriedades dos expoentes
- Use a definição de um expoente negativo
- Use notação científica
Simplifique as expressões usando as propriedades dos expoentes
Lembre-se de que um expoente indica multiplicação repetida da mesma quantidade. Por exemplo, na expressão\(a^m\), o expoente nos\(m\) diz quantas vezes usamos a base\(a\) como fator.
\[a^{m}= \underbrace{a \cdot a \cdot a \cdot \ldots \cdot a}_{\color{cyan}{\text{m factors}}} \nonumber\]
Por exemplo
\[(-9)^{5}= \underbrace{ (-9)\cdot (-9)\cdot (-9)\cdot (-9) \cdot (-9)}_{\color{cyan}{\text{5 factors}}} \nonumber\]
Vamos revisar o vocabulário para expressões com expoentes.
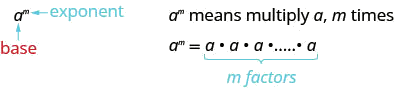
Isso é lido\(a\) ao\(m^{th}\) poder.
Na expressão\(a^m\), o expoente nos\(m\) diz quantas vezes usamos a base\(a\) como fator.
Quando combinamos termos semelhantes somando e subtraindo, precisamos ter a mesma base com o mesmo expoente. Mas quando você multiplica e divide, os expoentes podem ser diferentes e, às vezes, as bases também podem ser diferentes.
Primeiro, veremos um exemplo que leva à propriedade do produto.
|
\(x^{2} \cdot x^{3}\) |
||
| O que isso significa? |
\(\underbrace{x \cdot x}_{2 factors} \color{cyan}{\cdot} \underbrace{\color{black}{} x\cdot x \cdot x}_{3 factors}\) |
|
| \(x^{5}\) |
Observe que 5 é a soma dos expoentes, 2 e 3. Nós vemos\(x_2 \cdot x_3\) que é\(x^{2+3}\) ou\(x^5\).
A base permaneceu a mesma e adicionamos os expoentes. Isso leva à propriedade do produto para os expoentes.
Se a for um número real e\(m\) e\(n\) forem números inteiros, então
\[a^m·a^n=a^{m+n} \nonumber\]
Para multiplicar com bases semelhantes, adicione os expoentes.
Simplifique cada expressão:
- \(y^5·y^6\)
- \(2^x·2^{3x}\)
- \(2a^7·3a\).
- Resposta
-
ⓐ
Use a propriedade do produto,\(a^m·a^n=a^{m+n}\). 
Simplifique. 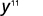
ⓑ
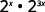
Use a propriedade do produto,\(a^m·a^n=a^{m+n}\). 
Simplifique. 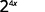
ⓒ
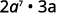
Reescrever,\(a=a^1\). 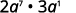
Use a propriedade comutativa e
use a propriedade do produto,\(a^m·a^n=a^{m+n}\).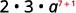
Simplifique. 
ⓓ
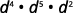
Adicione os expoentes, já que as bases são as mesmas. 
Simplifique. 
Simplifique cada expressão:
- \(b^9·b^8\)
- \(4^{2x}·4^x\)
- \(3p^5·4p\)
- \(x^6·x^4·x^8\).
- Resposta
-
ⓐ\(b^{17}\) ⓑ\(4^{3x}\) ⓒ\(12p^6\)
ⓓ\(x^{18}\)
Simplifique cada expressão:
- \(x^{12}·x4\)
- \(10·10^x\)
- \(2z·6z^7\)
- \(b^5·b^9·b^5\).
- Responda a
-
\(x^{16}\)
- Resposta b
-
\(10^{x+1}\)
- Resposta c
-
\(12z^8\)
- Resposta d
-
\(b^{19}\)
Agora, veremos uma propriedade de expoente para divisão. Como antes, tentaremos descobrir uma propriedade examinando alguns exemplos.
| Considere | \(\dfrac{x^5}{x^2}\) | e | \(\dfrac{x^2}{x^3}\) |
| O que eles querem dizer? | \(\dfrac{x·x·x·x·x}{x·x}\) | \(\dfrac{x·x}{x·x·x}\) | |
| Use a propriedade de frações equivalentes. | \(\dfrac{\cancel{x}·\cancel{x}·x·x·x}{\cancel{x}·\cancel{x}}\) | \(\dfrac{\cancel{x}·\cancel{x}·1}{\cancel{x}·\cancel{x}·x}\) | |
| Simplifique. | \(x^3\) |
\(\dfrac{1}{x}\) |
Observe que, em cada caso, as bases eram as mesmas e subtraímos os expoentes. Nós vemos\(\dfrac{x^5}{x^2}\) que é\(x^{5−2}\) ou\(x^3\). Nós vemos\(\dfrac{x^2}{x^3}\) que é ou\(\dfrac{1}{x}\). Quando o expoente maior estava no numerador, ficamos com fatores no numerador. Quando o expoente maior estava no denominador, ficamos com fatores no denominador — observe o numerador de 1. Quando todos os fatores no numerador tiverem sido removidos, lembre-se de que isso é realmente dividir os fatores em um, então precisamos de um 1 no numerador. \(\dfrac{\cancel{x}}{\cancel{x}}=1\). Isso leva à propriedade do quociente para os expoentes.
Se\(a\) for um número real\(a \neq 0\), e e\(m\) e\(n\) forem números inteiros, então
\[ \begin{array} {lllll} {\dfrac{a^m}{a^n}=a^{m−n},} &{m>n} &{\text{and}} &{\dfrac{a^m}{a^n}=\dfrac{1}{a^{n−m}},} &{n>m} \\ \nonumber \end{array} \]
Simplifique cada expressão:
- \(\dfrac{x^9}{x^7}\)
- \(\dfrac{3^{10}}{3^2}\)
- \(\dfrac{b^8}{b^{12}}\)
- \(\dfrac{7^3}{7^5}\).
- Resposta
-
Para simplificar uma expressão com um quociente, precisamos primeiro comparar os expoentes no numerador e no denominador.
ⓐ
Desde então\(9>7\), há mais fatores de\(x\) no numerador. 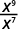
Use a propriedade do quociente,\(\dfrac{a^m}{a^n}=a^{m−n}\). 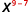
Simplifique. 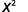
ⓑ
Desde então\(10>2\), há mais fatores de\(3\) no numerador. 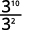
Use a propriedade do quociente,\(\dfrac{a^m}{a^n}=a^{m−n}\). 
Simplifique. 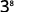
Observe que quando o expoente maior está no numerador, ficamos com fatores no numerador.
ⓒ
Desde então\(12>8\), existem mais fatores de bb no denominador. 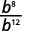
Use a propriedade do quociente,\(\dfrac{a^m}{a^n}=a^{m−n}\). 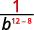
Simplifique. 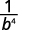
ⓓ
Desde então\(5>3\), há mais fatores de\(3\) no denominador. 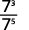
Use a propriedade do quociente,\(\dfrac{a^m}{a^n}=a^{m−n}\). 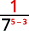
Simplifique. 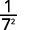
Simplifique. 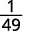
Observe que quando o expoente maior está no denominador, ficamos com fatores no denominador.
Simplifique cada expressão:
- \(\dfrac{x^{15}}{x^{10}}\)
- \(\dfrac{6^{14}}{6^5}\)
- \(\dfrac{x^{18}}{x^{22}}\)
- \(\dfrac{12^{15}}{12^{30}}\).
- Resposta
-
ⓐ\(x^5\)
ⓑ\(6^9\)
ⓒ\(\dfrac{1}{x^4}\)
ⓓ\(\dfrac{1}{12^{15}}\)
Simplifique cada expressão:
- \(\dfrac{y^{43}}{y^{37}}\)
- \(\dfrac{10^{15}}{10^{7}}\)
- \(\dfrac{m^7}{m^{15}}\)
- \(\dfrac{9^8}{9^{19}}\).
- Resposta
-
ⓐ\(y_6\)
ⓑ\(108\)
ⓒ\(1m8\)
ⓓ\(\dfrac{1}{9^{11}}\)
Um caso especial da propriedade do quociente é quando os expoentes do numerador e do denominador são iguais, como uma expressão como\(\dfrac{a^m}{a^m}\). Sabemos\(\dfrac{x}{x}=1\), para qualquer um,\(x(x\neq 0)\) já que qualquer número dividido por si só é 1.
A propriedade do quociente para expoentes nos mostra como simplificar\(\dfrac{a^m}{a^m}\). quando\(m>n\) e quando n<mn<m subtraindo expoentes. E se\(m=n\)? \(\dfrac{a^m}{a^m}\)Simplificaremos de duas maneiras para nos levar à definição da Propriedade do Expoente Zero. Em geral, para\(a \neq 0\):
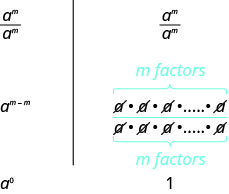
Vemos\(\dfrac{a^m}{a^m}\) simplificações para\(a^0\) e para 1. Então\(a^0=1\). Qualquer base diferente de zero elevada à potência de zero é igual\(1\).
Se\(a\) for um número diferente de zero, então\(a^0=1\).
Se\(a\) for um número diferente de zero, então\(a\) a potência de zero é igual\(1\).
Qualquer número diferente de zero elevado à potência zero é\(1\).
Neste texto, assumimos que qualquer variável que elevamos à potência zero não é zero.
Simplifique cada expressão: ⓐ\(9^0\) ⓑ\(n^0\).
- Resposta
-
A definição diz que qualquer número diferente de zero elevado à potência zero é\(1\).
ⓐ Use a definição do expoente zero. \(9^0 = 1\)
ⓑ Use a definição do expoente zero. \(n^0 = 1\)
Para simplificar a expressão\(n\) elevada à potência zero, usamos apenas a definição do expoente zero. O resultado é\(1\).
Simplifique cada expressão: ⓐ\(11^0\) ⓑ\(q^0\).
- Resposta
-
ⓐ 1
ⓑ 1
Simplifique cada expressão: ⓐ\(23^0\) ⓑ\(r^0\).
- Resposta
-
ⓐ 1
ⓑ 1
Use a definição de um expoente negativo
Vimos que a propriedade do quociente para expoentes tem duas formas, dependendo se o expoente é maior no numerador ou no denominador. E se apenas subtrairmos expoentes, independentemente de qual seja maior?
Vamos considerar\(\dfrac{x^2}{x^5}\). Subtraímos o expoente no denominador do expoente no numerador. Nós vemos\(\dfrac{x^2}{x^5}\) que é\(x^{2−5}\) ou\(x^{−3}\).
Também podemos simplificar\(\dfrac{x^2}{x^5}\) dividindo os fatores comuns:
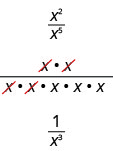
Isso implica isso\(x^{−3}=\dfrac{1}{x^3}\) e nos leva à definição de um expoente negativo. Se n for um número inteiro e\(a\neq 0\), então\(a^{−n}=\dfrac{1}{a^n}\).
Vamos agora ver o que acontece com uma fração cujo numerador é um e cujo denominador é um inteiro elevado a um expoente negativo.
\( \begin{array} {ll} {} &{\dfrac{1}{a^{-n}}} \\ {} &{} \\ {\text{Use the definition of a negative exponent, } a^{-n}= \dfrac{1}{a^n}} &{\dfrac{1}{\dfrac{1}{a^n}}} \\ {} &{} \\ {\text{Simplify the complex fraction.}} &{1·\dfrac{a^n}{1}} \\ {} &{} \\ {\text{Multiply.}} &{a^n} \\ \end{array} \)
Isso implica\(\dfrac{1}{a^{−n}}=a^n\) e é outra forma da definição de Propriedades de Expoentes Negativos.
Se\(n\) for um número inteiro e\(a\neq 0\), então\(a^{−n}=\dfrac{1}{a^n}\) ou\(\dfrac{1}{a^{−n}}=a^n\).
O expoente negativo nos diz que podemos reescrever a expressão tomando o inverso da base e depois alterando o sinal do expoente.
Qualquer expressão que tenha expoentes negativos não é considerada na forma mais simples. Usaremos a definição de um expoente negativo e outras propriedades dos expoentes para escrever a expressão somente com expoentes positivos.
Por exemplo, se depois de simplificar uma expressão terminarmos com a expressão\(x^{−3}\), daremos mais um passo e escreveremos\(\dfrac{1}{x^3}\). A resposta é considerada na forma mais simples quando tem apenas expoentes positivos.
Simplifique cada expressão: ⓐ\(x^{−5}\) ⓑ\(10^{−3}\) ⓒ\(\dfrac{1}{y^{−4}}\) ⓓ\(13^{−2}\).
- Resposta
-
ⓐ
\(\begin{array} {ll} {} &{x^{−5}} \\ {\text{Use the definition of a negative exponent, } a^{−n}=\dfrac{1}{a^n}.} &{\dfrac{1}{x^5}} \\ \end{array}\)
ⓑ
\(\begin{array} {ll} {} &{10^{-3}} \\ {\text{Use the definition of a negative exponent, }a^{−n}=\dfrac{1}{a^n}.} &{\dfrac{1}{10^3}} \\ {\text{Simplify.}} &{\dfrac{1}{1000}} \\ \end{array}\)
ⓒ
\(\begin{array} {ll} {} &{\dfrac{1}{y^{-4}}} \\ {\text{Use the property of a negative exponent, } \dfrac{1}{a^{−n}}=a^n.} &{y^4} \\ \end{array}\)
ⓓ
\(\begin{array} {ll} {} &{\dfrac{1}{3^{-2}}} \\ {\text{Use the property of a negative exponent, } \dfrac{1}{a^{−n}}=a^n.} &{3^2} \\ {\text{Simplify.}} &{9} \\ \end{array}\)
Simplifique cada expressão: ⓐ\(z^{−3}\) ⓑ\(10^{−7}\) ⓒ\(\dfrac{1}{p^{−8}}\) ⓓ\(\dfrac{1}{4^{−3}}\).
- Resposta
-
ⓐ\(\dfrac{1}{z^3}\) ⓑ\(\dfrac{1}{10^7}\) ⓒ\(p^8\) ⓓ\(64\)
Simplifique cada expressão: ⓐ\(n^{−2}\) ⓑ\(10^{−4}\) ⓒ\(\dfrac{1}{q^{−7}}\) ⓓ\(\dfrac{1}{2^{−4}}\).
- Resposta
-
ⓐ\(\dfrac{1}{n^2}\) ⓑ\(\dfrac{1}{10,000}\) ⓒ\(q^7\)
ⓓ\(16\)
Suponha que agora tenhamos uma fração elevada a um expoente negativo. Vamos usar nossa definição de expoentes negativos para nos levar a uma nova propriedade.
\(\begin{array} {ll} {} &{\left( \dfrac{3}{4} \right)^{-2}} \\ {} &{} \\ {\text{Use the definition of a negative exponent, } a^{−n}=\dfrac{1}{a^n}.} &{\dfrac{1}{\left( \dfrac{3}{4} \right)^{2}}} \\ {} &{} \\ {\text{Simplify the denominator.}} &{\dfrac{1}{\dfrac{9}{16}}} \\{} &{} \\ {\text{Simplify the complex fraction.}} &{\dfrac{16}{9}} \\ {} &{} \\ {\text{But we know that }\dfrac{16}{9}\text{ is } \left( \dfrac{4}{3} \right)^{2}.} &{} \\ {\text{This tells us that}} &{\left( \dfrac{3}{4} \right)^{-2} = \left( \dfrac{4}{3} \right)^{2}} \\ \end{array} \)
Para ir da fração original elevada a um expoente negativo até o resultado final, pegamos o inverso da base — a fração — e alteramos o sinal do expoente.
Isso nos leva ao quociente de uma propriedade de potência negativa.
Se\(a\) e\(b\) forem números reais,\(a\neq 0\),\(b\neq 0\) e\(n\) for um número inteiro, então
\[\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n \nonumber \].
Simplifique cada expressão: ⓐ\(\left( \dfrac{5}{7} \right)^{−2}\) ⓑ\(\left( −\dfrac{x}{y} \right)^{−3}\).
- Resposta
-
ⓐ
\(\begin{array} {ll} {} &{\left( \dfrac{5}{7}\right)^{-2}} \\ {\text{Use the Quotient to a Negative Exponent Property, } \left(\dfrac{a}{b} \right)^{−n}= \left( \dfrac{b}{a} \right)^n.} &{} \\ {\text{Take the reciprocal of the fraction and change the sign of the exponent.}} &{\left( \dfrac{7}{5}\right)^2} \\ {\text{Simplify.}} &{\dfrac{49}{25}} \\ \end{array} \)
ⓑ
\(\begin{array} {ll} {} &{\left( -\dfrac{x}{y}\right)^{-3}} \\ {\text{Use the Quotient to a Negative Exponent Property, } \left(\dfrac{a}{b} \right)^{−n}= \left( \dfrac{b}{a} \right)^n.} &{} \\ {\text{Take the reciprocal of the fraction and change the sign of the exponent.}} &{\left( -\dfrac{y}{x}\right)^3} \\ {\text{Simplify.}} &{-\dfrac{y^3}{x^3}} \\ \end{array} \)
Simplifique cada expressão: ⓐ\(\left(\dfrac{2}{3}\right)^{−4}\) ⓑ\(\left(−\dfrac{m}{n}\right)^{−2}\).
- Resposta
-
ⓐ\(\dfrac{81}{16}\) ⓑ\(\dfrac{n^2}{m^2}\)
Simplifique cada expressão: ⓐ\(\left(\dfrac{3}{5}\right)^{−3}\) ⓑ\(\left(−\dfrac{a}{b}\right)^{−4}\).
- Resposta
-
ⓐ\(\dfrac{125}{27}\) ⓑ\(\dfrac{b^4}{a^4}\)
Agora que temos expoentes negativos, usaremos a propriedade do produto com expressões que tenham expoentes negativos.
Simplifique cada expressão: ⓐ\(z^{−5}·z^{−3}\) ⓑ\((m^4n^{−3})(m^{−5}n^{−2})\) ⓒ\((2x^{−6}y^8)(−5x^5y^{−3})\).
- Resposta
-
ⓐ
\(\begin{array} {ll} {} &{z^{−5}·z^{−3}} \\ {\text{Add the exponents, since the bases are the same.}} &{z^{−5−3}} \\ {\text{Simplify.}} &{z^{−8}} \\ {\text{Use the definition of a negative exponent.}} &{\dfrac{1}{z^8}} \\ \end{array} \)
ⓑ
\(\begin{array} {ll} {} &{(m^4n^{−3})(m^{−5}n^{−2})} \\ {\text{Use the Commutative Property to get like}} &{} \\ {\text{bases together.}} &{m^4m^{−5}·n^{−2}n^{−3}} \\ {\text{Add the exponents for each base.}} &{m^{−1}·n^{−5}} \\ {\text{Take reciprocals and change the signs of the exponents.}} &{\dfrac{1}{m^1}·\dfrac{1}{n^5}} \\ {\text{Simplify.}} &{\dfrac{1}{mn^5}} \\ \end{array} \)
ⓒ
\(\begin{array} {ll} {} &{(2x^{−6}y^8)(−5x^5y^{−3})} \\ {\text{Rewrite with the like bases together.}} &{2(−5)·(x^{−6}x^5)·(y^8y^{−3})} \\ {\text{Multiply the coefficients and add the exponents}} &{} \\ {\text{of each variable.}} &{−10·x^{−1}·y5} \\ {\text{Use the definition of a negative exponent,} a^{−n}=\dfrac{1}{a^n}.} &{−10·\dfrac{1}{x}·y^5} \\ {\text{Simplify.}} &{−10y^5x} \\ \end{array} \)
Simplifique cada expressão:
ⓐ\(z^{−4}·z^{−5}\) ⓑ\((p^6q^{−2})(p^{−9}q^{−1})\) ⓒ\((3u^{−5}v^7)(−4u^4v^{−2})\).
- Resposta
-
ⓐ\(\dfrac{1}{z^9}\) ⓑ\(\dfrac{1}{p^3q^3}\) ⓒ\(−\dfrac{12v^5}{u}\)
Simplifique cada expressão:
ⓐ\(c^{−8}·c^{−7}\) ⓑ\((r^5s^{−3})(r^{−7}s^{−5})\) ⓒ\((−6c^{−6}d^4)(−5c^{−2}d^{−1})\).
- Resposta
-
ⓐ\(\dfrac{1}{c^15}\) ⓑ\(\dfrac{1}{r^2s^8}\) ⓒ\(\dfrac{30d^3}{c^8}\)
Agora vamos ver uma expressão exponencial que contém uma potência elevada a uma potência. Veja se você consegue descobrir uma propriedade geral.
\(\begin{array} {ll} {} &{(x^2)^3} \\ {\text{What does this mean?}} &{x^2·x^2·x^2} \\ \end{array} \)
| Quantos fatores no total? | 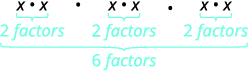 |
| Então nós temos | 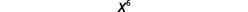 |
Observe que o 6 é o produto dos expoentes, 2 e 3. Vemos que\((x^2)^3\) é\(x^{2·3}\) ou\(x^6\).
Multiplicamos os expoentes. Isso leva à propriedade de poder dos expoentes.
Se\(a\) for um número real e\(m\) e\(n\) forem números inteiros, então
\[(a^m)^n=a^{m·n} \nonumber \]
Para elevar uma potência a uma potência, multiplique os expoentes.
Simplifique cada expressão: ⓐ\((y^5)^9\) ⓑ\((4^4)^7\) ⓒ\((y^3)^6(y^5)^4\).
- Resposta
-
ⓐ
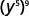
Use a propriedade Power,\((a^m)^n=a^{m·n}\). 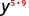
Simplifique. 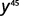
ⓑ
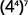
Use a propriedade Power. 
Simplifique. 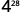
ⓒ
\(\begin{array} {ll} {} &{(y^3)^6(y^5)^4} \\ {\text{Use the Power Property.}} &{y^{18}·y^{20}} \\ {\text{Add the exponents.}} &{y^{38}} \\ \end{array} \)
Simplifique cada expressão: ⓐ\((b^7)^5\) ⓑ\((5^4)^3\) ⓒ\((a^4)^5(a^7)^4\).
- Resposta
-
ⓐ\(b^{35}\) ⓑ\(5^{12}\) ⓒ\(a^{48}\)
Simplifique cada expressão: ⓐ\((z^6)^9\) ⓑ\((3^7)^7\) ⓒ\((q^4)^5(q^3)^3\).
- Resposta
-
ⓐ\(z^{54}\) ⓑ\(3^{49}\) ⓒ\(q^{29}\)
Agora veremos uma expressão contendo um produto que é elevado a uma potência. Você consegue encontrar esse padrão?
\(\begin{array} {ll} {} &{(2x)^3} \\ {\text{What does this mean?}} &{2x·2x·2x} \\ {\text{We group the like factors together.}} &{2·2·2·x·x·x} \\ {\text{How many factors of 2 and of }}x &{2^3·x^3} \\ \end{array} \)
Observe que cada fator foi elevado à potência e\((2x)^3\) é\(2^3·x^3\).
O expoente se aplica a cada um dos fatores! Isso leva o produto a uma propriedade de poder para os expoentes.
Se\(a\) e\(b\) forem números reais e\(m\) for um número inteiro, então
\[(ab)^m=a^mb^m \nonumber \]
Para elevar um produto a uma potência, eleve cada fator a essa potência.
Simplifique cada expressão: ⓐ\((−3mn)^3\) ⓑ\((−4a^2b)^0\) ⓒ\((6k^3)^{−2}\) ⓓ\((5x^{−3})^2\).
- Resposta
-
ⓐ
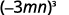
Use o poder de uma propriedade de produto,\((ab)^m=a^mb^m\). 
Simplifique. 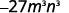
ⓑ
\(\begin{array} {ll} {} &{(−4a^2b)^0} \\ {\text{Use Power of a Product Property, }(ab)^m=a^mb^m.} &{(−4)^0(a^2)^0(b)^0} \\ {\text{Simplify.}} &{1·1·1} \\ {\text{Multiply.}} &{1} \\ \end{array} \)
ⓒ
\(\begin{array} {ll} {} &{(6k^3)^{−2}} \\ {\text{Use Power of a Product Property, }(ab)^m=a^mb^m.} &{(6)^{−2}(k^3)^{−2}} \\ {\text{Use the Power Property, }(a^m)^n=a^{m·n}.} &{6^{−2}k^{−6}} \\ {\text{Use the Definition of a negative exponent, }a^{−n}=\dfrac{1}{a^n}.} &{\dfrac{1}{6^2}·\dfrac{1}{k^6}} \\ {\text{Simplify.}} &{\dfrac{1}{36k^6}} \\ \end{array} \)
ⓓ
\(\begin{array} {ll} {} &{(5x^{−3})^2} \\ {\text{Use Power of a Product Property, }(ab)^m=a^mb^m.} &{5^2(x^{−3})^2} \\ {\text{Simplify.}} &{25·x^{−6}} \\ {\text{Rewrite }x−6 \text{using, }a^{−n}=\text{1}{a^n}.} &{25·\dfrac{1}{x^6}} \\ {\text{Simplify.}} &{\dfrac{25}{x^6}} \\ \end{array} \)
Simplifique cada expressão: ⓐ\((2wx)^5\) ⓑ\((−11pq3)^0\) ⓒ\((2b^3)^{−4}\) ⓓ\((8a^{−4})^2\).
- Resposta
-
ⓐ\(32w^5x^5\) ⓑ 1 ⓒ\(\dfrac{1}{16b^{12}}\)
ⓓ\(\dfrac{64}{a^8}\)
Simplifique cada expressão: ⓐ\((−3y)^3\) ⓑ\((−8m^2n^3)^0\) ⓒ\((−4x^4)^{−2}\) ⓓ\((2c^{−4})^3\).
- Responda
-
ⓐ\(−27y^3\) ⓑ 1 ⓒ\(\dfrac{1}{16x^8}\)
ⓓ\(8c^{12}\)
Agora veremos um exemplo que nos levará ao quociente de uma propriedade de poder.
\( \begin{array} {ll} {} &{\left( \dfrac{x}{y}\right)^3} \\ {\text{This means}} &{\dfrac{x}{y}·\dfrac{x}{y}·\dfrac{x}{y}} \\ {\text{Multiply the fractions.}} &{\dfrac{x·x·x}{y·y·y}} \\ {\text{Write with exponents.}} &{\dfrac{x^3}{y^3}} \\ \end{array} \)
Observe que o expoente se aplica tanto ao numerador quanto ao denominador.
Nós vemos que\(\left(\dfrac{x}{y}\right)^3\) é\(\dfrac{x^3}{y^3}\).
Isso leva ao quociente de uma propriedade de potência para expoentes.
Se\(a\) e\(b\) forem números reais,\(b\neq 0\), e\(m\) for um número inteiro, então
\[\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m} \nonumber \]
Para elevar uma fração a uma potência, eleve o numerador e o denominador para essa potência.
Simplifique cada expressão:
ⓐ\(\left(\dfrac{b}{3}\right)^4\) ⓑ\(\left(\dfrac{k}{j}\right)^{−3}\) ⓒ\(\left(\dfrac{2xy^2}{z}\right)^3\) ⓓ\(\left(\dfrac{4p^{−3}}{q^2}\right)^2\).
- Responda
-
ⓐ
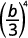
Use o quociente de uma propriedade de poder,\((ab)^m=a^mb^m\). 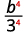
Simplifique. 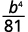
ⓑ
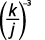
Eleve o numerador e o denominador à potência. 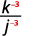
Use a definição de expoente negativo. 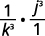
Multiplique. 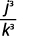
ⓒ
\(\begin{array} {ll} {} &{\left(\dfrac{2xy^2}{z}\right)^3} \\ {\text{Use Quotient to a Power Property, }\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m}.} &{\dfrac{(2xy^2)^3}{z^3}} \\ {\text{Use the Product to a Power Property, }(ab)^m=a^mb^m.} &{\dfrac{8x^3y^6}{z^3}} \\ \end{array} \)
ⓓ
\(\begin{array} {ll} {} &{\left(\dfrac{4p^{−3}}{q^2}\right)^2} \\ {\text{Use Quotient to a Power Property, }\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m}.} &{\dfrac{(4p^{−3})^2}{(q^2)^2}} \\ {\text{Use the Product to a Power Property, }(ab)^m=a^mb^m.} &{\dfrac{4^2(p^{−3})^2}{(q^2)^2}} \\ {\text{Simplify using the Power Property, }(a^m)^n=a^{m·n}.} &{\dfrac{16p^{−6}}{q^4}} \\ {\text{Use the definition of negative exponent.}} &{\dfrac{16}{q^4}·\dfrac{1}{p^6}} \\ {\text{Simplify.}} &{\dfrac{16}{p^6q^4}} \\ \end{array} \)
Simplifique cada expressão:
ⓐ\(\left(\dfrac{p}{10}\right)^4\) ⓑ\(\left(\dfrac{m}{n}\right)^{−7}\) ⓒ\(\left(\dfrac{3ab^3}{c^2}\right)^4\) ⓓ\(\left(\dfrac{3x^{−2}}{y^3}\right)^3\).
- Responda
-
ⓐ\(\dfrac{p^4}{10000}\) ⓑ\(\dfrac{n^7}{m^7}\)
ⓒ\(\dfrac{81a^4b^{12}}{c^8}\) ⓓ\(\dfrac{27}{x^6y^9}\)
Simplifique cada expressão:
ⓐ\(\left(\dfrac{−2}{q}\right)^3\) ⓑ\(\left(\dfrac{w}{x}\right)^{−4}\) ⓒ\(\left(\dfrac{xy^3}{3z^2}\right)^2\) ⓓ\(\left(\dfrac{2m^{−2}}{n^{−2}}\right)^3\).
- Responda
-
ⓐ\(\dfrac{−8}{q^3}\) ⓑ\(\dfrac{x^4}{w^4}\) ⓒ\(\dfrac{x^2y^6}{9z^4}\)
ⓓ\( \dfrac{8n^6}{m^6}\)
Agora temos várias propriedades para expoentes. Vamos resumi-los e, em seguida, faremos mais alguns exemplos que usam mais de uma das propriedades.
Se\(a\) e\(b\) forem números reais e\(m\) e\(n\) forem números inteiros, então
| Propriedade | Descrição |
|---|---|
| Propriedade do produto | \(a^m·a^n=a^{m+n}\) |
| Propriedade de poder | \((a^m)^n=a^{m·n}\) |
| Produto em potência | \((ab)^n=a^nb^n\) |
| Propriedade do quociente | \(\dfrac{a^m}{a^n}=a^{m−n},a\neq 0\) |
| Propriedade de expoente zero | \(a^0=1,a \neq 0\) |
| Quociente de uma propriedade de poder | \(\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m},b \neq 0 \) |
| Propriedades dos expoentes negativos | \(a^{−n}=\dfrac{1}{a^n}\)e\(\dfrac{1}{a^{−n}}=a^n\) |
| Quociente para um expoente negativo | \(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\) |
Simplifique cada expressão aplicando várias propriedades:
ⓐ\((3x^2y)^4(2xy^2)^3\) ⓑ\(\dfrac{(x^3)^4(x^{−2})^5}{(x^6)^5}\) ⓒ\(\left(\dfrac{2xy^2}{x^3y^{−2}}\right)^2 \left(\dfrac{12xy^3}{x^3y^{−1}}\right)^{−1}\).
- Responda
-
ⓐ
\(\begin{array} {ll} {} &{(3x^2y)^4(2xy^2)^3} \\ {} &{} \\ {\text{Use the Product to a Power Property, }(ab)^m=a^mb^m.} &{(3^4x^8y^4)(2^3x^3y^6)} \\ {} &{} \\ {\text{Simplify.}} &{(81x^8y^4)(8x^3y^6)} \\ {} &{} \\ {\text{Use the Commutative Property.}} &{81·8·x^8·x^3·y^4·y^6} \\ {} &{} \\ {\text{Multiply the constants and add the exponents.}} &{648x^{11}y^{10}} \\ \end{array} \)
ⓑ
\( \begin{array} {ll} {} &{\dfrac{(x^3)^4(x^{−2})^5}{(x^6)^5}} \\ {\text{Use the Power Property, }(a^m)^n=a^{m·n}.} &{(x^{12})(x^{−10})(x^{30})} \\ {\text{Add the exponents in the numerator.}} &{\dfrac{x^2}{x^{30}}} \\ {\text{Use the Quotient Property, }\dfrac{a^m}{a^n}=\dfrac{1}{a^{n−m}}.} &{\dfrac{1}{x^{28}}} \\ \end{array} \)
ⓒ
\( \begin{array} {ll} {} &{\left(\dfrac{2xy^2}{x^3y^{−2}}\right)^2 \left(\dfrac{12xy^3}{x^3y^{−1}}\right)^{−1}} \\ {\text{Simplify inside the parentheses first.}} &{\left(\dfrac{2y^4}{x^2}\right)^2\left(\dfrac{12y^4}{x^2}\right)^{−1}} \\ {\text{Use the Quotient to a Power Property, }\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m}.} &{\dfrac{(2y^4)^2}{(x^2)^2}\dfrac{(12y^4)^{−1}}{(x^2)^{−1}}} \\ {\text{Use the Product to a Power Property, }(ab)^m=a^mb^m.} &{\dfrac{4y^8}{x^4}·\dfrac{12^{−1}y^{−4}}{x^{−2}}} \\ {\text{Simplify.}} &{\dfrac{4y^4}{12x^2}} \\ {\text{Simplify.}} &{\dfrac{y^4}{3x^2}} \\ \end{array} \)
Simplifique cada expressão:
ⓐ\((c^4d^2)^5(3cd^5)^4\) ⓑ\(\dfrac{(a^{−2})^3(a^2)^4}{(a^4)^5}\) ⓒ\(\left(\dfrac{3xy^2}{x^2y^{−3}}\right)^2\)
- Responda
-
ⓐ\(81c^{24}d^{30}\) ⓑ\(\dfrac{1}{a^{18}}\)
ⓒ\(\dfrac{9y^{10}}{x^2}\)
Simplifique cada expressão:
ⓐ\((a^3b^2)^6(4ab^3)^4\) ⓑ\(\dfrac{(p^{−3})^4(p^5)^3}{(p^7)^6}\) ⓒ\(\left(\dfrac{4x^3y^2}{x^2y^{−1}}\right)^2\left(\dfrac{8xy^{−3}}{x^2y}\right)^{−1}\).
- Responda
-
ⓐ\(256a^{22}b^{24}\) ⓑ\(\dfrac{1}{p^{39}}\)
ⓒ\(2x^3y^{10}\)
Use notação científica
Trabalhar com números muito grandes ou muito pequenos pode ser complicado. Como nosso sistema numérico é a base dez, podemos usar potências de dez para reescrever números muito grandes ou muito pequenos para facilitar o trabalho com eles. Considere os números 4.000 e 0,004.
Usando o valor posicional, podemos reescrever os números 4.000 e 0,004. Sabemos que 4.000 significa\(4\times1,000\) e 0,004 significa\(4\times\dfrac{1}{1,000}\).
Se escrevermos 1.000 como uma potência de dez na forma exponencial, podemos reescrever esses números desta forma:
| 4.000 | \(4\times1,000\) | \(4\times103\) | |
| 0,004 | \(4\times\dfrac{1}{1,000}\) | \(4\times\dfrac{1}{103}\) | \(4\times10^{−3}\) |
Quando um número é escrito como um produto de dois números, onde o primeiro fator é um número maior ou igual a um, mas menor que dez, e o segundo fator é uma potência de 10 escrita em forma exponencial, diz-se que está em notação científica.
Um número é expresso em notação científica quando é da forma
\[\begin{array} {llllllllllll} {a} &{\times} &{10^n} &{\text{where}} &{1} &{\leq} &{a} &{<} &{10} &{\text{and}} &{n} &{\text{is an integer.}} \\ \nonumber \end{array}\]
É comum na notação científica usar como sinal de\(\times\) multiplicação, mesmo que evitemos usar esse sinal em outros lugares da álgebra.
Se observarmos o que aconteceu com o ponto decimal, podemos ver um método para converter facilmente a notação decimal em notação científica.

Em ambos os casos, o decimal foi movido 3 casas para obter o primeiro fator entre 1 e 10.
A potência de 10 é positiva quando o número é maior que\(1: 4,000=4\times10^3\)
A potência de 10 é negativa quando o número está entre 0 e 1:\(0.004=4\times10^{−3}\)
- Mova o ponto decimal para que o primeiro fator seja maior ou igual a 1, mas menor que 10.
- Conte o número de casas decimais,\(n\), em que o ponto decimal foi movido.
- Escreva o número como um produto com uma potência de 10. Se o número original for.
- maior que 1, a potência de 10 será\(10^n\).
- entre 0 e 1, a potência de 10 será\(10^{−n}\).
- Verifique.
Escreva em notação científica: ⓐ\(37,000\) ⓑ\(0.0052\).
- Responda
-
ⓐ
O número original, 37.000, é maior que 1
, então teremos uma potência positiva de 10.37.000 Mova o ponto decimal para obter 3,7, um número
entre 1 e 10.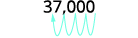
Conte o número de casas decimais em que o ponto
foi movido.
Escreva como um produto com uma potência de 10. 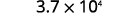
\(\begin{array} {ll} {} &{3.7\times 10^4 } \\ {\text{Check:}} &{3.7 \times 10,000 } \\ {} &{37,000} \\ \end{array} \)
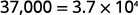
ⓑ
O número original, 0,0052, está entre 0
e 1, então teremos uma potência negativa de 10.0,0052 Mova o ponto decimal para obter 5,2, um número
entre 1 e 10.
Conte o número de casas decimais em que o ponto
foi movido.
Escreva como um produto com uma potência de 10. 
\(\begin{array} {ll} {\text{Check:}} &{5.2\times10^{−3}} \\ {} &{5.2\times\dfrac{1}{10^3}} \\ {} &{5.2\times\dfrac{1}{1000}} \\ {} &{5.2\times 0.001} \\ {} &{0.0052} \\ \end{array} \)
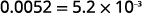
Escreva em notação científica: ⓐ 96.000 ⓑ 0.0078.
- Responda
-
ⓐ\(9.6\times 10^4\) ⓑ\(7.8\times 10^{−3}\)
Escreva em notação científica: ⓐ 48.300 ⓑ 0.0129.
- Responda
-
ⓐ\(4.83\times10^4\)
ⓑ\(1.29\times10^{−2}\)
Como podemos converter da notação científica para a forma decimal? Vamos ver dois números escritos em notação científica e ver.
\[\begin{array} {lll} {9.12\times10^4} &{} &{9.12\times10^{−4}} \\ {9.12\times10,000} &{} &{9.12\times0.0001} \\ {91,200} &{} &{0.000912} \\ \nonumber \end{array} \]
Se observarmos a localização do ponto decimal, podemos ver um método fácil de converter um número da notação científica para a forma decimal.

Em ambos os casos, o ponto decimal se moveu para 4 casas. Quando o expoente era positivo, o decimal era movido para a direita. Quando o expoente era negativo, o ponto decimal se movia para a esquerda.
- Determine o expoente\(n\),, no fator 10.
- Mova as casas\(n\) decimais, adicionando zeros, se necessário.
- Se o expoente for positivo, mova as casas\(n\) decimais para a direita.
- Se o expoente for negativo, mova as casas\(|n|\) decimais para a esquerda.
- Verifique.
Converta para a forma decimal: ⓐ\(6.2\times10^3\) ⓑ\(−8.9\times 10^{−2}\).
- Responda
-
ⓐ
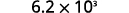
Determine o expoente\(n\),, no fator 10. O expoente é 3. Como o expoente é positivo, mova o ponto
decimal 3 casas para a direita.
Adicione zeros conforme necessário para espaços reservados. 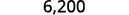
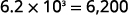
ⓑ

Determine o expoente\(n\),, no fator 10. O expoente é −2.−2. Como o expoente é negativo, mova o ponto
decimal 2 casas para a esquerda.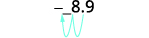
Adicione zeros conforme necessário para espaços reservados. 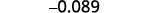
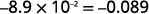
Converta para a forma decimal: ⓐ\(1.3\times 10^3\) ⓑ\(−1.2\times 10^{−4}\).
- Responda
-
ⓐ 1.300 ⓑ\(−0.00012\)
Converta para a forma decimal: ⓐ\(−9.5\times 10^4\) ⓑ\(7.5\times 10^{−2}\).
- Responda
-
ⓐ\(−950,000\) ⓑ 0,075
Quando os cientistas realizam cálculos com números muito grandes ou muito pequenos, eles usam a notação científica. A notação científica fornece uma maneira de os cálculos serem feitos sem escrever muitos zeros. Veremos como as propriedades dos expoentes são usadas para multiplicar e dividir números em notação científica.
Multiplique ou divida conforme indicado. Escreva as respostas em formato decimal: ⓐ\((−4\times10^5)(2\times10^{−7})\) ⓑ\(\dfrac{9\times10^3}{3\times10^{−2}}\).
- Responda
-
ⓐ
\(\begin{array} {ll} {} &{(−4\times10^5)(2\times10^{−7})} \\ {\text{Use the Commutative Property to rearrange the factors.}} &{−4·2·10^5·10^{−7}} \\ {\text{Multiply.}} &{−8\times10^{−2}} \\ {} &{} \\ {\text{Change to decimal form by moving the decimal two}} &{} \\ {\text{places left.}} &{−0.08} \\ \end{array}\)
ⓑ
\(\begin{array} {ll} {} &{\dfrac{9\times10^3}{9\times10^{−2}}} \\ {\text{Separate the factors, rewriting as the product of two}} &{} \\ {\text{fractions.}} &{\dfrac{9}{3}\times\dfrac{10^3}{10^{−2}}} \\ {\text{Divide.}} &{3\times10^5} \\ {\text{Change to decimal form by moving the decimal five}} &{} \\ {\text{places right.}} &{300,000} \\ \end{array}\)
Multiplique ou divida conforme indicado. Escreva as respostas em formato decimal:
ⓐ\((−3\times10^5)(2\times10^{−8})\) ⓑ\(\dfrac{8\times10^2}{4\times10^{−2}}\).
- Responda
-
ⓐ\(−0.006\) ⓑ 20.000
Multiplique ou divida conforme indicado. Escreva as respostas em formato decimal:
ⓐ\((−3\times10^{−2})(3\times10^{−1})\) ⓑ\(\dfrac{8\times10^4}{2\times10^{−1}}\).
- Responda
-
ⓐ\(−0.009\) ⓑ 400.000
Acesse esses recursos on-line para obter instruções adicionais e praticar o uso de propriedades de multiplicação de expoentes.
- Propriedades dos expoentes
- Expoentes negativos
- Notação científica
Conceitos-chave
- Notação exponencial
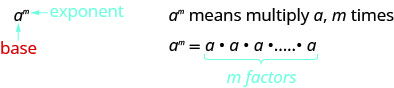
Isso é lido\(a\) à\(m^{th}\) potência.
Na expressão\(a^m\), o expoente nos\(m\) diz quantas vezes usamos a base\(a\) como fator. - Propriedade do produto para expoentes
Se\(a\) for um número real e\(m\) e\(n\) forem números inteiros, então\[a^m·a^n=a^{m+n} \nonumber \]
Para multiplicar com bases semelhantes, adicione os expoentes. - Propriedade do quociente para expoentes
Se\(a\) for um número real\(a\neq 0\), e e\(m\) e\(n\) forem números inteiros, então\[\begin{array} {lllll} {\dfrac{a^m}{a^n}=a^{m−n},} &{m>n} &{\text{and}} &{\dfrac{a^m}{a^n}=\dfrac{1}{a^{n−m}},} &{n>m}\\ \nonumber \end{array}\]
- Expoente zero
- Se\(a\) for um número diferente de zero, então\(a^0=1\).
- Se\(a\) for um número diferente de zero, então\(a\) a potência de zero é igual\(1\).
- Qualquer número diferente de zero elevado à potência zero é\(1\).
- Expoente negativo
- Se\(n\) for um número inteiro e\(a\neq 0\), então\(a^{−n}=\dfrac{1}{a^n}\) ou\(\dfrac{1}{a^{−n}}=a^n\).
- Quociente para uma propriedade de expoente negativo
Se\(a\) e\(b\) forem números reais\(a\neq 0\),,\(b\neq 0\) e\(n\) for um número inteiro, então\[(ab)^{−n}=(ba)^n\nonumber \]
- Propriedade de potência para expoentes
Se\(a\) for um número real e\(m\) e\(n\) forem números inteiros, então\[(a^m)^n=a^{m·n}\nonumber \]
Para elevar uma potência a uma potência, multiplique os expoentes. - Produto para uma propriedade de potência para expoentes
Se\(a\) e\(b\) forem números reais e\(m\) for um número inteiro, então\[(ab)^m=a^mb^m \nonumber \]
Para elevar um produto a uma potência, eleve cada fator a essa potência. - Quociente de uma propriedade de potência para expoentes
Se\(a\) e\(b\) forem números reais\(b\neq0\),, e\(m\) for um número inteiro, então\[\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m} \nonumber \]
Para elevar uma fração a uma potência, eleve o numerador e o denominador para essa potência. - Resumo das propriedades do expoente
Se\(a\) e\(b\) forem números reais e\(m\) e\(n\) forem números inteiros, entãoPropriedade Descrição Propriedade do produto \(a^m·a^n=a^{m+n}\) Propriedade de poder \((a^m)^n=a^{m·n}\) Produto em potência \((ab)^n=a^nb^n\) Propriedade do quociente \(\dfrac{a^m}{a^n}=a^{m−n}, a\neq 0\) Propriedade de expoente zero \(a^0=1,a\neq 0\) Quociente de uma propriedade de poder: \(\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m}, b\neq 0\) Propriedades dos expoentes negativos \(a^{−n}=\dfrac{1}{a^n}\)e\(\dfrac{1}{a^{−n}}=a^n\) Quociente para um expoente negativo \(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\) - Notação científica
Um número é expresso em notação científica quando é da forma\[a\space\times\space10^n \text{ where }1\leq a<10\text{ and } n \text{ is an integer.} \nonumber \]
- Como converter um decimal em notação científica.
- Mova o ponto decimal para que o primeiro fator seja maior ou igual a 1, mas menor que 10.
- Conte o número de casas decimais,\(n\), em que o ponto decimal foi movido.
- Escreva o número como um produto com uma potência de 10. Se o número original for.
- maior que 1, a potência de 10 será\(10^n\).
- entre 0 e 1, a potência de 10 será\(10^{−n}\).
- Verifique.
- Como converter a notação científica na forma decimal.
- Determine o expoente\(n\),, no fator 10.
- Mova as casas\(n\) decimais, adicionando zeros, se necessário.
- Se o expoente for positivo, mova as casas\(n\) decimais para a direita.
- Se o expoente for negativo, mova as casas\(|n|\) decimais para a esquerda.
- Verifique.
Glossário
- Propriedade do produto
- De acordo com a Propriedade do Produto,\(a\)\(a\) até o\(m\) vezes\(a\) igual\(a\) ao\(m\) mais\(n\).
- Propriedade de poder
- De acordo com a Propriedade do Poder,\(a\)\(m\)\(a\) para\(n\) os iguais aos\(m\) tempos\(n\).
- Produto em potência
- De acordo com o Produto para uma Propriedade\(b\) de Poder,\(a\) tempos entre parênteses\(m\) iguais\(a\)\(b\) aos\(m\) tempos para\(m\) o.
- Propriedade do quociente
- De acordo com a Propriedade do Quociente,\(a\) o\(m\) dividido por\(a\) para o é\(n\) igual\(a\) ao\(m\) menos\(n\), desde que não\(a\) seja zero.
- Propriedade de expoente zero
- De acordo com a Propriedade do Expoente Zero,\(a\) até o zero é\(1\) tão longo quanto não\(a\) é zero.
- Quociente de uma propriedade de poder
- De acordo com o Quociente de uma Propriedade de Poder,\(a\) dividido por\(b\) entre parênteses, a potência de\(m\) é igual\(a\) à\(m\) dividida por\(b\) com a,\(m\) desde que não\(b\) seja zero.
- Propriedades dos expoentes negativos
- De acordo com as Propriedades dos Expoentes Negativos,\(a\) para o negativo\(n\) é igual a\(1\) dividido por\(a\) para o\(n\) e\(1\) dividido por\(a\) para o negativo\(n\) é igual\(a\) a\(n\) a.
- Quociente para um expoente negativo
- A elevação de um quociente para um expoente negativo ocorre quando\(a\) dividido por\(b\) entre parênteses elevado à potência de menos\(n\) igual\(b\) dividido por\(a\) entre parênteses à potência de\(n\).