Skip to main content
Global

4.8E: Exercícios

  1. Last updated
  2. Save as PDF
  • Page ID
    183249

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    A prática leva à perfeição

    Determine se um par ordenado é uma solução de um sistema de desigualdades lineares

    Nos exercícios a seguir, determine se cada par pedido é uma solução para o sistema.

    1. \(\left\{\begin{array} {l} 3x+y>5\\2x−y\leq 10\end{array}\right.\)

    ⓐ\((3,−3)\)
    ⓑ\((7,1)\)

    2. \(\left\{\begin{array} {l} 4x−y<10\\−2x+2y>−8\end{array}\right.\)

    ⓐ\((5,−2)\)
    ⓑ\((−1,3)\)

    Responda

    ⓐ falso ⓑ verdadeiro

    3. \(\left\{\begin{array} {l} y>\frac{2}{3}x−5\\x+\frac{1}{2}y\leq 4\end{array}\right.\)

    ⓐ\((6, −4)\)
    ⓑ\((3, 0)\)

    4. \(\left\{\begin{array} {l} y<\frac{3}{2}x+3\\ \frac{3}{4}x−2y<5\end{array}\right.\)

    ⓐ\((−4,−1)\)
    ⓑ\((8, 3)\)

    Responda

    ⓐ falso ⓑ verdadeiro

    5. \(\left\{\begin{array} {l} 7x+2y>14\\5x−y\leq 8\end{array}\right.\)

    ⓐ\((2, 3)\)
    ⓑ\((7, −1)\)

    6. \(\left\{\begin{array} {l} 6x−5y<20\\−2x+7y>−8 \end{array}\right.\)

    ⓐ\((1, −3)\)
    ⓑ\((−4, 4)\)

    Responda

    ⓐ falso ⓑ verdadeiro

    Resolva um sistema de desigualdades lineares por meio de gráficos

    Nos exercícios a seguir, resolva cada sistema representando gráficos.

    7. \(\left\{\begin{array} {l} y\leq 3x+2\\y>x−1\end{array}\right.\)

    8. \(\left\{\begin{array} {l} y<−2x+2\\y\geq −x−1\end{array}\right.\)

    Responda

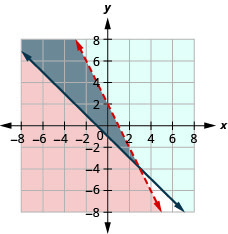
    A figura mostra o gráfico das desigualdades y menor que menos duas vezes x mais dois e y maior ou igual a menos x menos um. Duas linhas que se cruzam são mostradas, uma em vermelho e outra em azul. A área delimitada pelas duas linhas é mostrada em cinza.

    A solução é a região cinza.

    9. \(\left\{\begin{array} {l} y<2x−1\\y\leq −\frac{1}{2}x+4\end{array}\right.\)

    10. \(\left\{\begin{array} {l} y\geq −\frac{2}{3}x+2\\y>2x−3\end{array}\right.\)

    Responda

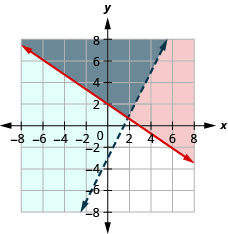
    A figura mostra o gráfico das desigualdades y maiores ou iguais a menos dois por três x mais dois e y maior que duas vezes x menos três. Duas linhas que se cruzam, uma em vermelho e outra em azul, são mostradas. A região delimitada por eles é mostrada em cinza.

    A solução é a região cinza.

    11. \(\left\{\begin{array} {l} x−y>1\\y<−\frac{1}{4}x+3\end{array}\right.\)

    12. \(\left\{\begin{array} {l} x+2y<4\\y<x−2\end{array}\right.\)

    Responda

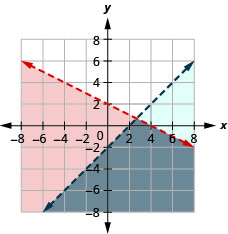
    A figura mostra o gráfico das desigualdades x menos duas vezes y menor que quatro e y menor que x menos dois. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. A área delimitada pelas linhas é mostrada em cinza.

    A solução é a região cinza.

    13. \(\left\{\begin{array} {l} 3x−y\geq 6\\y\geq −\frac{1}{2}x\end{array}\right.\)

    14. \(\left\{\begin{array} {l} x+4y\geq 8\\y\leq \frac{3}{4}x\end{array}\right.\)

    Responda

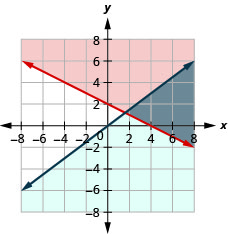
    A figura mostra o gráfico das desigualdades duas vezes x mais quatro vezes y maior ou igual a oito e y menor ou igual a menos três quartos de x. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. A área delimitada pelas linhas é mostrada em cinza. É a solução.

    A solução é a região cinza.

    15. \(\left\{\begin{array} {l} 2x−5y<10\\3x+4y\geq 12\end{array}\right.\)

    16. \(\left\{\begin{array} {l} 3x−2y\leq 6\\−4x−2y>8\end{array}\right.\)

    Responda

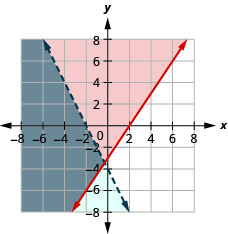
    A figura mostra o gráfico das desigualdades três vezes x menos duas vezes y menor ou igual a seis e menos quatro vezes x menos duas vezes y maior que oito. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. A área delimitada pelas linhas é mostrada em cinza. É a solução.

    A solução é a região cinza.

    17. \(\left\{\begin{array} {l} 2x+2y>−4\\−x+3y\geq 9\end{array}\right.\)

    18. \(\left\{\begin{array} {l} 2x+y>−6\\−x+2y\geq −4\end{array}\right.\)

    Responda

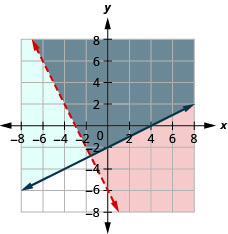
    A figura mostra o gráfico das desigualdades duas vezes x mais y maior que menos seis e menos x mais duas vezes y maior ou igual a menos quatro. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. A área delimitada pelas linhas é mostrada em cinza. É a solução.

    A solução é a região cinza.

    19. \(\left\{\begin{array} {l} x−2y<3\\y\leq 1\end{array}\right.\)

    20. \(\left\{\begin{array} {l} x−3y>4\\y\leq −1\end{array}\right.\)

    Responda

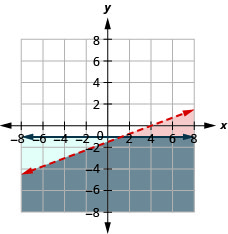
    A figura mostra o gráfico das desigualdades x menos três vezes y maior que quatro e y menor ou igual a menos um. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. A área delimitada pelas linhas é mostrada em cinza. É a solução.

    A solução é a região cinza.

    21. \(\left\{\begin{array} {l} y\geq −\frac{1}{2}x−3\\x\leq 2\end{array}\right.\)

    22. \(\left\{\begin{array} {l} y\leq −\frac{2}{3}x+5\\x\geq 3\end{array}\right.\)

    Resposta

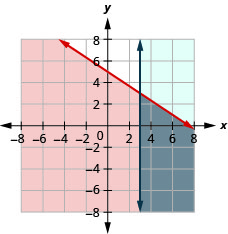
    A figura mostra o gráfico da desigualdade y menor ou igual a menos dois por três vezes x mais cinco e x maior ou igual a três. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. A área delimitada pelas linhas é mostrada em cinza. É a solução.

    A solução é a região cinza.

    23. \(\left\{\begin{array} {l} y\geq \frac{3}{4}x−2\\y<2\end{array}\right.\)

    24. \(\left\{\begin{array} {l} y\leq −\frac{1}{2}x+3\\y<1\end{array}\right.\)

    Resposta

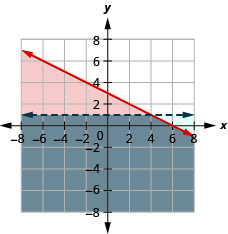
    A figura mostra o gráfico das desigualdades y menores ou iguais a menos metade x mais três e y menor que um. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. A área delimitada pelas linhas é mostrada em cinza. É a solução.

    A solução é a região cinza.

    25. \(\left\{\begin{array} {l} 3x−4y<8\\x<1\end{array}\right.\)

    26. \(\left\{\begin{array} {l} −3x+5y>10\\x>−1\end{array}\right.\)

    Resposta

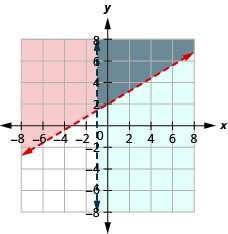
    A figura mostra o gráfico das desigualdades menos três vezes x mais cinco vezes y maior que dez e x maior que menos um. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. A área delimitada pelas linhas é mostrada em cinza. É a solução.

    A solução é a região cinza.

    27. \(\left\{\begin{array} {l} x\geq 3\\y\leq 2\end{array}\right.\)

    28. \(\left\{\begin{array} {l} x\leq −1\\y\geq 3\end{array}\right.\)

    Resposta

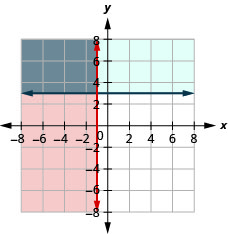
    A figura mostra o gráfico das desigualdades x menor ou igual a menos um e y maior ou igual a três. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. A área delimitada pelas linhas é mostrada em cinza. É a solução.

    A solução é a região cinza.

    29. \(\left\{\begin{array} {l} 2x+4y>4 \\ y\leq −\frac{1}{2}x−2\end{array}\right.\)

    30. \(\left\{\begin{array} {l} x−3y\geq 6\\y>\frac{1}{3}x+1\end{array}\right.\)

    Resposta

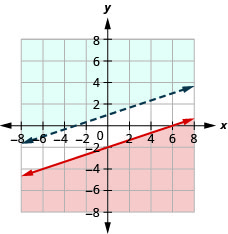
    A figura mostra o gráfico das desigualdades x menos três vezes y maior ou igual a seis e y maior que um terço de x mais um. Duas linhas que não se cruzam, uma em azul e outra em vermelho, são mostradas.

    Sem solução.

    31. \(\left\{\begin{array} {l} −2x+6y<0\\6y>2x+4\end{array}\right.\)

    32. \(\left\{\begin{array} {l} −3x+6y>12\\4y\leq 2x−4\end{array}\right.\)

    Resposta

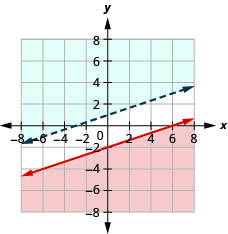
    A figura mostra o gráfico das desigualdades menos três vezes x mais seis vezes y maior que doze e quatro vezes y menor ou igual a duas vezes x menos quatro. Duas linhas que não se cruzam, uma em azul e outra em vermelho, são mostradas.

    Sem solução.

    33. \(\left\{\begin{array} {l} y\geq −3x+2\\3x+y>5\end{array}\right.\)

    34. \(\left\{\begin{array} {l} y\geq \frac{1}{2}x−1\\−2x+4y\geq 4\end{array}\right.\)

    Resposta

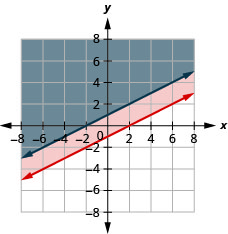
    A figura mostra o gráfico das desigualdades y maiores ou iguais a menos metade x menos um e menos duas vezes x mais quatro vezes y maior ou igual a quatro. Duas linhas que não se cruzam, uma em azul e outra em vermelho, são mostradas. A área da solução é mostrada em cinza.

    A solução é a região cinza.

    35. \(\left\{\begin{array} {l} y\leq −\frac{1}{4}x−2\\x+4y<6\end{array}\right.\)

    36. \(\left\{\begin{array} {l} y\geq 3x−1\\−3x+y>−4\end{array}\right.\)

    Resposta

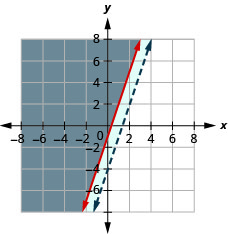
    A figura mostra o gráfico das desigualdades y maiores ou iguais a três vezes x menos um e menos três vezes x mais y maior que menos quatro. Duas linhas que não se cruzam, uma em azul e outra em vermelho, são mostradas. A área da solução é mostrada em cinza.

    A solução é a região cinza.

    37. \(\left\{\begin{array} {l} 3y>x+2\\−2x+6y>8\end{array}\right.\)

    38. \(\left\{\begin{array} {l} y<\frac{3}{4}x−2\\−3x+4y<7\end{array}\right.\)

    Resposta

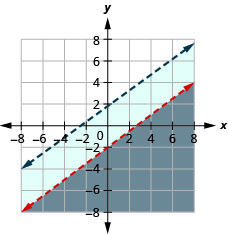
    A figura mostra o gráfico das desigualdades y menor que três por quarto x menos dois e menos três x mais quatro y menor que sete. Duas linhas que não se cruzam, uma em azul e outra em vermelho, são mostradas. A área da solução é mostrada em cinza.

    A solução é a região cinza.

    Resolva aplicações de sistemas de desigualdades

    Nos exercícios a seguir, traduza para um sistema de desigualdades e resolva.

    39. Caitlyn vende seus desenhos na feira do condado. Ela quer vender pelo menos 60 desenhos e tem retratos e paisagens. Ela vende os retratos por $15 e as paisagens por $10. Ela precisa vender pelo menos $800 em desenhos para obter lucro.

    ⓐ Escreva um sistema de desigualdades para modelar essa situação.
    ⓑ Faça um gráfico do sistema.
    ⓒ Ela terá lucro se vender 20 retratos e 35 paisagens?
    ⓓ Ela terá lucro se vender 50 retratos e 20 paisagens?

    40. Jake não quer gastar mais do que $50 em sacos de fertilizante e turfa para seu jardim. O fertilizante custa $2 por saco e o musgo de turfa custa $5 por saco. A van de Jake pode conter no máximo 20 malas.

    ⓐ Escreva um sistema de desigualdades para modelar essa situação.
    ⓑ Faça um gráfico do sistema.
    ⓒ Ele pode comprar 15 sacos de fertilizante e 4 sacos de turfa?
    ⓓ Ele pode comprar 10 sacos de fertilizante e 10 sacos de turfa?

    Resposta

    ⓐ\(\left\{\begin{array} {l} f\geq 0 \\ p\geq 0 \\ f+p\leq 202 \\ f+5p\leq 50\end{array}\right.\)
    ⓑ

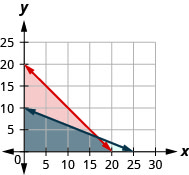
    A figura mostra o gráfico das desigualdades f mais p menor ou igual a vinte e dois f e cinco p menor ou igual a cinquenta. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. Uma área é mostrada em cinza.

    ⓒ sim
    ⓓ não

    41. Reiko precisa enviar seus cartões e pacotes de Natal e quer manter seus custos de envio em não mais do que $500. O número de cartões é pelo menos 4 a mais do que o dobro do número de pacotes. O custo do envio de um cartão (com fotos anexadas) é de $3 e, para um pacote, o custo é de $7.

    ⓐ Escreva um sistema de desigualdades para modelar essa situação.
    ⓑ Faça um gráfico do sistema.
    ⓒ Ela pode enviar 60 cartões e 26 pacotes?
    ⓓ Ela pode enviar 90 cartões e 40 pacotes?

    42. Juan está estudando para seus exames finais em química e álgebra. Ele sabe que só tem 24 horas para estudar e levará pelo menos três vezes mais tempo para estudar álgebra do que química.

    ⓐ Escreva um sistema de desigualdades para modelar essa situação.
    ⓑ Faça um gráfico do sistema.
    ⓒ Ele pode passar 4 horas em química e 20 horas em álgebra?
    ⓓ Ele pode passar 6 horas em química e 18 horas em álgebra?

    Resposta

    ⓐ\(\left\{\begin{array} {l} c\geq 0\\a\geq 0\\c+a\leq 24\\a\geq 3c\end{array}\right.\)
    ⓑ

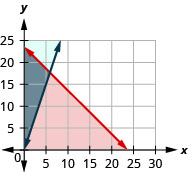
    A figura mostra o gráfico das desigualdades c mais a menor ou igual a vinte e quatro e a maior ou igual a três vezes c. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. Uma área é mostrada em cinza.

    ⓒ sim
    ⓓ não

    43. Jocelyn está grávida e, portanto, precisa ingerir pelo menos 500 calorias a mais por dia do que o normal. Ao comprar mantimentos um dia com um orçamento de $15 para a comida extra, ela compra bananas com 90 calorias cada e barras de granola de chocolate com 150 calorias cada. As bananas custam $0,35 cada e as barras de granola custam $2,50 cada.

    ⓐ Escreva um sistema de desigualdades para modelar essa situação.
    ⓑ Faça um gráfico do sistema.
    ⓒ Ela poderia comprar 5 bananas e 6 barras de granola?
    ⓓ Ela poderia comprar 3 bananas e 4 barras de granola?

    44. Mark está tentando construir massa muscular e, portanto, ele precisa comer pelo menos 80 gramas adicionais de proteína por dia. Uma garrafa de água proteica custa $3,20 e uma barra de proteína custa $1,75. A água proteica fornece 27 gramas de proteína e a barra fornece 16 gramas. Se ele tiver $10 dólares para gastar

    ⓐ Escreva um sistema de desigualdades para modelar essa situação.
    ⓑ Faça um gráfico do sistema.
    ⓒ Ele poderia comprar 3 garrafas de água proteica e 1 barra de proteína?
    ⓓ Ele não poderia comprar garrafas de água proteica e 5 barras de proteína?

    Resposta

    ⓐ\(\left\{\begin{array} {l} w\geq 0\\b\geq 0\\27w+16b>80\\3.20w+1.75b\leq 10\end{array}\right.\)
    ⓑ

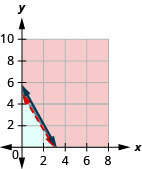
    A figura mostra o gráfico das desigualdades vinte e sete vezes w mais dezesseis vezes b maior que oitenta e três pontos dois vezes w mais um ponto sete cinco b menor ou igual a dez. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. Uma área é mostrada em cinza.

    ⓒ não
    ⓓ sim

    45. Jocelyn deseja aumentar o consumo de proteína e a ingestão calórica. Ela deseja ter pelo menos 35 gramas a mais de proteína por dia e não mais do que 200 calorias adicionais por dia. Uma onça de queijo cheddar tem 7 gramas de proteína e 110 calorias. Uma onça de queijo parmesão tem 11 gramas de proteína e 22 calorias.

    ⓐ Escreva um sistema de desigualdades para modelar essa situação.
    ⓑ Faça um gráfico do sistema.
    ⓒ Ela poderia comer 1 onça de queijo cheddar e 3 onças de queijo parmesão?
    ⓓ Ela poderia comer 2 onças de queijo cheddar e 1 onça de queijo parmesão?

    46. Mark está aumentando sua rotina de exercícios correndo e caminhando pelo menos 4 milhas por dia. Seu objetivo é queimar no mínimo 1500 calorias desse exercício. Caminhar queima 270 calorias/milha e correr queima 650 calorias.

    ⓐ Escreva um sistema de desigualdades para modelar essa situação.
    ⓑ Faça um gráfico do sistema.
    ⓒ Ele poderia atingir seu objetivo andando 3 milhas e correndo 1 milha?
    ⓓ Poderia ser seu objetivo andando 2 milhas e correndo 2 milhas?

    Resposta

    ⓐ\(\left\{\begin{array} {l} w\geq 0\\r\geq 0\\w+r\geq 4\\270w+650r\geq 1500\end{array}\right.\)
    ⓑ

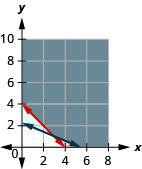
    A figura mostra o gráfico das desigualdades w mais r maior ou igual a quatro e dois setenta w mais seis cinquenta r maior ou igual a quinhentos. Duas linhas que se cruzam, uma em azul e outra em vermelho, são mostradas. Uma área é mostrada em cinza.

    ⓒ não
    ⓓ sim

    exercícios de escrita

    47. Faça um gráfico da desigualdade\(x−y\geq 3\). Como você sabe qual lado da linha\(x−y=3\) deve estar sombreado?

    48. Faça um gráfico do sistema\(\left\{\begin{array} {l} x+2y\leq 6 \\ y\geq −\frac{1}{2}x−4\end{array}\right.\). O que significa a solução?

    Resposta

    As respostas podem variar.

    Verificação automática

    ⓐ Depois de concluir os exercícios, use esta lista de verificação para avaliar seu domínio dos objetivos desta seção.

    A figura mostra uma tabela com quatro colunas e quatro linhas. A primeira linha é a linha do título. Os quatro títulos são eu posso..., com confiança, com alguma ajuda e Não — eu não entendo! Na segunda linha da primeira coluna, o texto diz “determine se um par ordenado é uma solução de um sistema de desigualdades lineares”. Na terceira linha da primeira coluna, o texto diz “resolver aplicações de sistemas de desigualdades”.

    ⓑ O que essa lista de verificação diz sobre seu domínio desta seção? Quais etapas você tomará para melhorar?