Capítulo 4 Exercícios de revisão

Last updated
Save as PDF

Page ID: 183170

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Exercícios de revisão de

Resolva sistemas de equações lineares com duas variáveis

Determine se um par ordenado é uma solução de um sistema de equações.

Nos exercícios a seguir, determine se os pontos a seguir são soluções para um determinado sistema de equações.

1. $\left\{ \begin{array} {l} x+3y=−9\\2x−4y=12 \end{array} \right.$

ⓐ$(−3,−2)$
ⓑ$(0,−3)$

2. $\left\{ \begin{array} {l} x+y=8\\y=x−4 \end{array} \right.$

ⓐ$(6,2)$
ⓑ$(9,−1)$

Resposta: ⓐ sim ⓑ não

Resolva um sistema de equações lineares por meio de gráficos

Nos exercícios a seguir, resolva os seguintes sistemas de equações representando graficamente.

3. $\left\{ \begin{array} {l} 3x+y=6\\x+3y=−6 \end{array} \right.$

4. $\left\{ \begin{array} {l} x+4y=−1\\x=3 \end{array} \right.$

Resposta

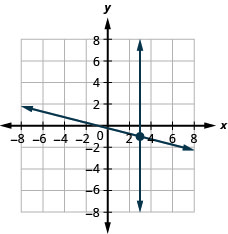
$A figura mostra o gráfico das equações x mais quatro vezes y igual a menos um e x igual a três. Duas linhas que se cruzam são mostradas.$

$(3,−1)$

5. $\left\{ \begin{array} {l} 2x−y=5\\4x−2y=10 \end{array} \right.$

6. $\left\{ \begin{array} {l} −x+2y=4\\y=\frac{1}{2}x−3 \end{array} \right.$

Resposta

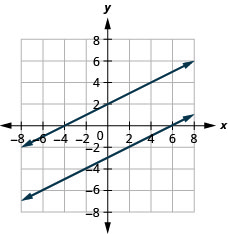
$A figura mostra o gráfico das equações menos x mais duas vezes y igual a quatro e y igual a meio x menos três. Duas linhas paralelas são mostradas.$

sem solução

Nos exercícios a seguir, sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações.

7. $\left\{ \begin{array} {l} y=\frac{2}{5}x+2\\−2x+5y=10 \end{array} \right.$

8. $\left\{ \begin{array} {l} 3x+2y=6\\y=−3x+4 \end{array} \right.$

Resposta: uma solução, sistema consistente, equações independentes

9. $\left\{ \begin{array} {l} 5x−4y=0\\y=\frac{5}{4}x−5 \end{array} \right.$

Resolva um sistema de equações por substituição

Nos exercícios a seguir, resolva os sistemas de equações por substituição.

10. $\left\{ \begin{array} {l} 3x−2y=2\\y=\frac{1}{2}x+3 \end{array} \right.$

Resposta: $(4,5)$

11. $\left\{ \begin{array} {l} x−y=0\\2x+5y=−14 \end{array} \right.$

12. $\left\{ \begin{array} {l} y=−2x+7\\y=\frac{2}{3}x−1 \end{array} \right.$

Resposta: $(3,1)$

13. $\left\{ \begin{array} {l} y=−5x\\5x+y=6 \end{array} \right.$

14. $\left\{ \begin{array} {l} y=−\frac{1}{3}x+2\\x+3y=6 \end{array} \right.$

Resposta: infinitas soluções

Resolva um sistema de equações por eliminação

Nos exercícios a seguir, resolva os sistemas de equações por eliminação

15. $\left\{ \begin{array} {l} x+y=12\\x−y=−10 \end{array} \right.$

16. $\left\{ \begin{array} {l} 3x−8y=20\\x+3y=1 \end{array} \right.$

Resposta: $(4,−1)$

17. $\left\{ \begin{array} {l} 9x+4y=2\\5x+3y=5 \end{array} \right.$

18. $\left\{ \begin{array} {l} \frac{1}{3}x−\frac{1}{2}y=1\\ \frac{3}{4}x−y=\frac{5}{2} \end{array} \right.$

Resposta: $(6,2)$

19. $\left\{ \begin{array} {l} −x+3y=8\\2x−6y=−20 \end{array} \right.$

Escolha o método mais conveniente para resolver um sistema de equações lineares

Nos exercícios a seguir, decida se seria mais conveniente resolver o sistema de equações por substituição ou eliminação.

20. $\left\{ \begin{array} {l} 6x−5y=27\\3x+10y=−24 \end{array} \right.$

Resposta: eliminação

21. $\left\{ \begin{array} {l} y=3x−9\\4x−5y=23 \end{array} \right.$

Resolva aplicações com sistemas de equações

Resolva aplicativos de tradução direta

Nos exercícios a seguir, traduza para um sistema de equações e resolva.

22. Mollie quer plantar 200 bulbos em seu jardim, todos íris e tulipas. Ela quer plantar três vezes mais tulipas do que íris. Quantas íris e quantas tulipas ela deve plantar?

Resposta: 50 íris e 150 tulipas

23. Ashanti recebeu ofertas de vagas de duas companhias telefônicas. A primeira empresa paga um salário de $22.000 mais uma comissão de $100 por cada contrato vendido. O segundo paga um salário de $28.000 mais uma comissão de $25 por cada contrato vendido. Quantos contratos precisariam ser vendidos para que o pagamento total fosse o mesmo?

24. Leroy passou 20 minutos correndo e 40 minutos pedalando e queimou 600 calorias. No dia seguinte, Leroy trocou horários, fazendo 40 minutos de corrida e 20 minutos de bicicleta e queimou a mesma quantidade de calorias. Quantas calorias foram queimadas para cada minuto de corrida e quantas para cada minuto de ciclismo?

Resposta: 10 calorias para correr e 10 calorias para andar de bicicleta

25. Troy e Lisa estavam comprando material escolar. Cada um comprou quantidades diferentes do mesmo caderno e calculadora. Troy comprou quatro notebooks e cinco calculadoras por $116. Lisa comprou dois notebooks e três calculadoras por 68 dólares. Descubra o custo de cada notebook e cada pen drive.

Resolva aplicações de geometria

Nos exercícios a seguir, traduza para um sistema de equações e resolva.

26. A diferença de dois ângulos suplementares é de 58 graus. Encontre as medidas dos ângulos.

Resposta: 119, 61

27. Dois ângulos são complementares. A medida do ângulo maior é cinco a mais do que quatro vezes a medida do ângulo menor. Encontre as medidas dos dois ângulos.

28. A medida de um dos pequenos ângulos de um triângulo reto é 15 menor que o dobro da medida do outro ângulo pequeno. Encontre a medida dos dois ângulos.

Resposta: $35°$e$55°$

29. Becca está pendurando uma guirlanda floral de 28 pés nos dois lados e no topo de uma pérgola para se preparar para um casamento. A altura é quatro pés a menos que a largura. Encontre a altura e a largura da pérgola.

30. O perímetro de um parque retangular da cidade é de 1428 pés. O comprimento é 78 pés a mais do que o dobro da largura. Encontre o comprimento e a largura do parque.

Resposta: o comprimento é 450 pés, a largura é 264 pés

Resolva aplicações de movimento uniforme

Nos exercícios a seguir, traduza para um sistema de equações e resolva.

31. Sheila e Lenore estavam dirigindo para a casa da avó. Lenore saiu uma hora depois de Sheila. Sheila dirigiu a uma taxa de 45 mph, e Lenore dirigiu a uma taxa de 60 mph. Quanto tempo vai demorar para Lenore alcançar Sheila?

32. Bob saiu de casa, andando de bicicleta a uma taxa de 10 milhas por hora para ir ao lago. Cheryl, sua esposa, saiu 45 minutos (34 (34 horas) depois, dirigindo seu carro a uma taxa de 25 milhas por hora. Quanto tempo Cheryl levará para alcançar Bob?

Resposta: $12$uma hora

33. Marcus pode dirigir seu barco 36 milhas rio abaixo em três horas, mas leva quatro horas para retornar rio acima. Encontre a taxa do barco em água parada e a taxa da corrente.

34. Um jato de passageiros pode voar 804 milhas em 2 horas com vento de cauda, mas apenas 776 milhas em 2 horas em um vento contrário. Encontre a velocidade do jato no ar parado e a velocidade do vento.

Resposta: a taxa do jato é 395 mph, a taxa do vento é 7 mph

Resolva aplicações de mistura com sistemas de equações

Resolva aplicações de mistura com sistemas de equações

Para os exercícios a seguir, traduza para um sistema de equações e resolva.

35. Lynn pagou um total de $2.780 por 261 ingressos para o teatro. Os ingressos para estudantes custam $10 e os ingressos para adultos custam $15. Quantos ingressos para estudantes e quantos ingressos para adultos Lynn comprou?

36. Priam tem moedas de dez centavos e moedas em um porta-copos em seu carro. O valor total das moedas é de $4,21. O número de moedas de dez centavos é três a menos de quatro vezes o número de centavos. Quantos centavos e quantos centavos estão na xícara?

Resposta: 41 centavos e 11 centavos

37. Yumi quer fazer 12 xícaras de mistura de festa usando doces e nozes. Seu orçamento exige que o mix de festa lhe custe $1,29 por xícara. Os doces custam $2,49 por xícara e as nozes custam $0,69 por xícara. Quantas xícaras de doces e quantas xícaras de nozes ela deve usar?

38. Um cientista precisa de 70 litros de uma solução de 40% de álcool. Ele tem uma solução de 30% e 60% disponível. Quantos litros das soluções de 30% e quantos litros das soluções de 60% ele deve misturar para fazer a solução de 40%?

Resposta: $46\frac{2}{3}$litros de solução de 30%,$23\frac{1}{3}$ litros de solução de 60%

Resolver aplicativos de interesse

Para os exercícios a seguir, traduza para um sistema de equações e resolva.

39. Jack tem $12.000 para investir e quer ganhar 7,5% de juros ao ano. Ele colocará parte do dinheiro em uma conta poupança que ganha 4% ao ano e o restante em uma conta de CD que ganha 9% ao ano. Quanto dinheiro ele deve colocar em cada conta?

40. Quando se formar na faculdade, Linda ficará devendo 43.000 dólares em empréstimos estudantis. A taxa de juros dos empréstimos federais é de 4,5% e a taxa dos empréstimos bancários privados é de 2%. O total de juros que ela deve por um ano foi de $1.585. Qual é o valor de cada empréstimo?

Resposta: $29.000 para o empréstimo federal, $14.000 para o empréstimo privado

Resolva sistemas de equações com três variáveis

Resolva sistemas de equações com três variáveis

Nos exercícios a seguir, determine se o triplo solicitado é uma solução para o sistema.

41. $\left\{ \begin{array} {l} 3x−4y−3z=2\\2x−6y+z=3\\2x+3y−2z=3 \end{array} \right.$

ⓐ$(2,3,−1)$
ⓑ$(3,1,3)$

42. $\left\{ \begin{array} {l} y=\frac{2}{3}x−2\\x+3y−z=15\\x−3y+z=−2 \end{array} \right.$

ⓐ$(−6,5,\frac{1}{2})$
ⓑ$(5,\frac{4}{3},−3)$

Resposta: ⓐ não ⓑ sim

Resolva um sistema de equações lineares com três variáveis

Nos exercícios a seguir, resolva o sistema de equações.

43. $\left\{ \begin{array} {l} 3x−5y+4z=5\\5x+2y+z=0\\2x+3y−2z=3 \end{array} \right.$

44. $\left\{ \begin{array} {l} x+\frac{5}{2}y+z=−2\\2x+2y+\frac{1}{2}z=−4\\ \frac{1}{3}x−y−z=1 \end{array} \right.$

Resposta: $(−3,2,−4)$

45. $\left\{ \begin{array} {l} 5x+3y=−6\\2y+3z=−1\\7x+z=1 \end{array} \right.$

46. $\left\{ \begin{array} {l} 2x+3y+z=12\\x+y+z=9\\3x+4y+2z=20 \end{array} \right.$

Resposta: sem solução

47. $\left\{ \begin{array} {l} −x−3y+2z=14\\−x+2y−3z=−4\\3x+y−2z=6 \end{array} \right.$

Resolva aplicações usando sistemas de equações lineares com três variáveis

48. Depois de assistir a um jogo da liga principal de beisebol, os clientes costumam comprar lembranças. Se uma família comprar 4 camisetas, um boné e 1 bicho de pelúcia, o total é de $135. Um casal compra 2 camisetas, um boné e 3 bichos de pelúcia para suas sobrinhas e gasta $115. Outro casal compra 2 camisetas, um boné e 1 bicho de pelúcia e o total é de $85. Qual é o custo de cada item?

Resposta: $25, 20, 15$

Resolva sistemas de equações usando matrizes

Escreva a matriz aumentada para um sistema de equações.

Escreva cada sistema de equações lineares como uma matriz aumentada.

49. $\left\{ \begin{array} {l} 3x−y=−1\\−2x+2y=5 \end{array} \right.$

50. $\left\{ \begin{array} {l} 4x+3y=−2\\x−2y−3z=7\\2x−y+2z=−6 \end{array} \right.$

Resposta: $\left[ \begin{matrix} 4&3&0&−2\\1&−2&−3&7\\2&−1&2&−6 \end{matrix} \right]$

Escreva o sistema de equações que corresponde à matriz aumentada.

51. $\left[ \begin{array} {cc|c} 2&−4&-2\\3&−3&-1 \end{array} \right]$

52. $\left[ \begin{array} {ccc|c} 1&0&−3&-1\\1&−2&0&-2\\0&−1&2&3 \end{array} \right]$

Resposta: $\left\{ \begin{array} {l} x−3z=−1\\x−2y=−27\\−y+2z=3 \end{array} \right.$

Nos exercícios a seguir, execute as operações indicadas nas matrizes aumentadas.

53. $\left[ \begin{array} {cc|c} 4&−6&-3\\3&2&1 \end{array} \right]$

ⓐ Troque as linhas 2 e 1.
ⓑ Multiplique a linha 1 por 4.
ⓒ Multiplique a linha 2 por 3 e adicione à linha 1.

54. $\left[ \begin{array} {ccc|c} 1&−3&−2&4\\2&2&−1&-3\\4&−2&−3&-1 \end{array} \right]$

ⓐ Troque as linhas 2 e 3.
ⓑ Multiplique a linha 1 por 2.
ⓒ Multiplique a linha 3 por −2−2 e adicione à linha 2.

Resposta: ⓐ$\left[ \begin{matrix} 1&−3&−2&4\\4&−2&−3&−1\\2&2&−1&−3 \end{matrix} \right]$

ⓑ$\left[ \begin{matrix} 2&−6&−4&8\\4&−2&−3&−1\\2&2&−1&−3 \end{matrix} \right]$

ⓒ$\left[ \begin{matrix} 2&−6&−4&8\\4&−2&−3&−1\\0&−6&−1&5 \end{matrix} \right]$

Resolva sistemas de equações usando matrizes

Nos exercícios a seguir, resolva cada sistema de equações usando uma matriz.

55. $\left\{ \begin{array} {l} 4x+y=6\\x−y=4 \end{array} \right.$

56. $\left\{ \begin{array} {l} 2x−y+3z=−3\\−x+2y−z=10\\x+y+z=5 \end{array} \right.$

Resposta: $(−2,5,−2)$

57. $\left\{ \begin{array} {l} 2y+3z=−1\\5x+3y=−6\\7x+z=1 \end{array} \right.$

58. $\left\{ \begin{array} {l} x+2y−3z=−1\\x−3y+z=1\\2x−y−2z=2 \end{array} \right.$

Resposta: sem solução

59. $\left\{ \begin{array} {l} x+y−3z=−1\\y−z=0\\−x+2y=1 \end{array} \right.$

Resolva sistemas de equações usando determinantes

Avalie o determinante de uma matriz 2 × 2

No exercício a seguir, avalie a determinação da matriz quadrada.

60. $\left[ \begin{matrix} 8&−4\\5&−3 \end{matrix} \right]$

Resposta: $−4$

Avalie o determinante de uma matriz 3 × 3

No exercício a seguir, encontre e avalie os menores indicados.

61. $\left| \begin{matrix} −1&−3&2\\4&−2&−1\\−2&0&−3 \end{matrix} \right|$; Encontre o menor ⓐ$a_1$ ⓑ$b_1$ ⓒ$c_2$

No exercício a seguir, avalie cada determinante expandindo por menores ao longo da primeira linha.

62. $\left| \begin{matrix} −2&−3&−4\\5&−6&7\\−1&2&0 \end{matrix} \right|$

Resposta: $21$No exercício a seguir, avalie cada determinante por meio da expansão por menores.

63. $\left| \begin{matrix} 3&5&4\\−1&3&0\\−2&6&1 \end{matrix} \right|$

Use a regra de Cramer para resolver sistemas de equações

Nos exercícios a seguir, resolva cada sistema de equações usando a regra de Cramer

64. $\left\{ \begin{array} {l} x−3y=−9\\2x+5y=4 \end{array} \right.$

Resposta: $(−3,2)$

65. $\left\{ \begin{array} {l} 4x−3y+z=7\\2x−5y−4z=3\\3x−2y−2z=−7 \end{array} \right.$

66. $\left\{ \begin{array} {l} 2x+5y=4\\3y−z=3\\4x+3z=−3 \end{array} \right.$

Resposta: $(−3,2,3)$

67. $\left\{ \begin{array} {l} x+y−3z=−1\\y−z=0\\−x+2y=1 \end{array} \right.$

68. $\left\{ \begin{array} {l} 3x+4y−3z=−2\\2x+3y−z=−1\\2x+y−2z=6 \end{array} \right.$

Resposta: inconsistentes

Resolva aplicativos usando determinantes

Nos exercícios a seguir, determine se os pontos fornecidos são colineares.

69. $(0,2)$,$(−1,−1)$, e$(−2,4)$

Representação gráfica de sistemas de desigualdades lineares

Determine se um par ordenado é uma solução de um sistema de desigualdades lineares

Nos exercícios a seguir, determine se cada par pedido é uma solução para o sistema.

70. $\left\{ \begin{array} {l} 4x+y>6\\3x−y\leq 12 \end{array} \right.$

ⓐ$(2,−1)$
ⓑ$(3,−2)$

Resposta: ⓐ sim ⓑ não

71. $\left\{ \begin{array} {l} y>\frac{1}{3}x+2\\x−\frac{1}{4}y\leq 10 \end{array} \right.$

ⓐ$(6,5)$
ⓑ$(15,8)$

Resolva um sistema de desigualdades lineares por meio de gráficos

Nos exercícios a seguir, resolva cada sistema representando gráficos.

72. $\left\{ \begin{array} {l} y<3x+1\\y\geq −x−2 \end{array} \right.$

Resposta

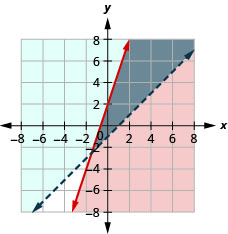
$A figura mostra o gráfico das desigualdades y menores que três vezes x mais um e y maior ou igual a menos x menos dois. Duas linhas que se cruzam, uma em vermelho e outra em azul, são mostradas. Uma área é mostrada em cinza.$

A solução é a região cinza.

73. $\left\{ \begin{array} {l} x−y>−1\\y<\frac{1}{3}x−2 \end{array} \right.$

74. $\left\{ \begin{array} {l} 2x−3y<6\\3x+4y\geq 12 \end{array} \right.$

Resposta

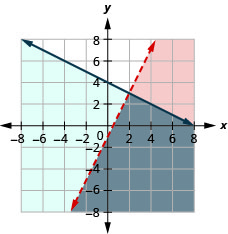
$A figura mostra o gráfico das desigualdades duas vezes x menos três vezes y menos seis e três vezes x mais quatro vezes y maior ou igual a doze. Duas linhas que se cruzam, uma em vermelho e outra em azul, são mostradas. Uma área é mostrada em cinza.$

A solução é a região cinza.

75. $\left\{ \begin{array} {l} y\leq −\frac{3}{4}x+1\\x\geq −5 \end{array} \right.$

76. $\left\{ \begin{array} {l} x+3y<5\\y\geq -\frac{1}{3}x+6 \end{array} \right.$

Resposta

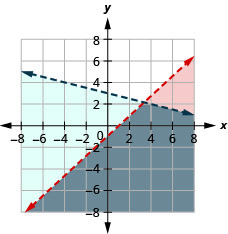
$A figura mostra o gráfico das desigualdades x mais três vezes y menor que cinco e y maior ou igual a menos um terço x mais seis. Duas linhas paralelas, uma em vermelho e outra em azul, são mostradas. Uma área é mostrada em cinza.$

Sem solução.

77. $\left\{ \begin{array} {l} y\geq 2x−5\\−6x+3y>−4 \end{array} \right.$

Resolva aplicações de sistemas de desigualdades

Nos exercícios a seguir, traduza para um sistema de desigualdades e resolva.

78. Roxana fabrica pulseiras e colares e os vende no mercado dos fazendeiros. Ela vende as pulseiras por $12 cada e os colares por $18 cada. No mercado no próximo fim de semana, ela terá espaço para exibir no máximo 40 peças e precisará vender pelo menos $500 para obter lucro.

ⓐ Escreva um sistema de desigualdades para modelar essa situação.
ⓑ Faça um gráfico do sistema.
ⓒ Ela deveria exibir 26 pulseiras e 14 colares?
ⓓ Ela deveria exibir 39 pulseiras e 1 colar?

Resposta

ⓐ$\left\{ \begin{array} {l} b\geq 0\\ n\geq 0\\ b+n\leq 40\\12b+18n\geq 500 \end{array} \right.$
ⓑ

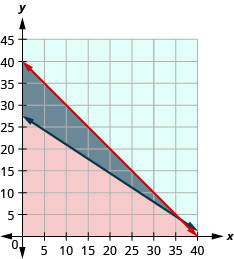
$A figura mostra o gráfico de b mais n igual a quarenta e doze b mais dezoito n igual a quinhentos. Duas linhas que se cruzam, uma em vermelho e outra em azul, são mostradas. Uma área é mostrada em cinza.$

ⓒ sim
ⓓ não

79. Annie tem um orçamento de $600 para comprar livros de capa dura e livros de capa dura para sua sala de aula. Ela quer que o número de livros de capa dura seja pelo menos 5 a mais do que três vezes o número de livros de bolso. Livros de bolso custam $4 cada e livros de capa dura custam $15 cada.

ⓐ Escreva um sistema de desigualdades para modelar essa situação.
ⓑ Faça um gráfico do sistema.
ⓒ Ela pode comprar 8 livros de bolso e 40 livros de capa dura?
ⓓ Ela pode comprar 10 livros de bolso e 37 livros de capa dura?

Teste prático do capítulo

Nos exercícios a seguir, resolva os seguintes sistemas representando graficamente.

1. $\left\{ \begin{array} {l} x−y=5\\x+2y=−4 \end{array} \right.$

Resposta

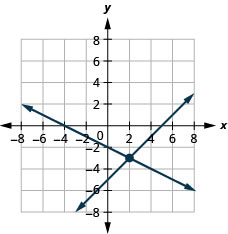
$A figura mostra o gráfico das desigualdades h igual a três p mais cinco e quatro vezes p mais quinze vezes h igual a seiscentas. Duas linhas que se cruzam, uma em vermelho e outra em azul, são mostradas. Uma área é mostrada em cinza.$

$(2,−3)$

2. $\left\{ \begin{array} {l} x−y>−2\\y\leq 3x+1 \end{array} \right.$

Nos exercícios a seguir, resolva cada sistema de equações. Use substituição ou eliminação.

3. $\left\{ \begin{array} {l} x+4y=6\\−2x+y=−3 \end{array} \right.$

Resposta: $(2,1)$

4. $\left\{ \begin{array} {l} −3x+4y=2\\5x−5y=−23 \end{array} \right.$

5. $\left\{ \begin{array} {l} x+y−z=−1\\2x−y+2z=8\\−3x+2y+z=−9 \end{array} \right.$

Resposta: $(2,−2,1)$

Resolva o sistema de equações usando uma matriz.

6. $\left\{ \begin{array} {l} 2x+y=7\\x−2y=6 \end{array} \right.$

7. $\left\{ \begin{array} {l} −3x+y+z=−4\\−x+2y−2z=1\\2x−y−z=−1 \end{array} \right.$

Resposta: $(5,7,4)$

Resolva usando a regra de Cramer.

8. $\left\{ \begin{array} {l} 3x+y=−3\\2x+3y=6 \end{array} \right.$

9. Avalie o determinante expandindo por menores:

$\left| \begin{matrix} 3&−2&−2\\2&−1&4\\−1&0&−3 \end{matrix} \right|$

Resposta: $99$

Nos exercícios a seguir, traduza para um sistema de equações e resolva.

10. Greg está remando sua canoa rio acima, contra a corrente, até um local de pesca a 10 milhas de distância. Se ele remar rio acima por 2,5 horas e sua viagem de volta durar 1,25 horas, encontre a velocidade da corrente e sua velocidade de remo em água parada.

11. Um farmacêutico precisa de 20 litros de uma solução salina de 2%. Ele tem uma solução de 1% e 5% disponível. Quantos litros das soluções de 1% e quantos litros das soluções de 5% ela deve misturar para fazer a solução de 2%?

Resposta: 15 litros de solução de 1%, 5 litros de solução de 5%

12. Arnold investiu $64.000, alguns com 5,5% de juros e o restante com 9%. Quanto ele investiu em cada taxa se recebesse $4.500 em juros em um ano?

13. O grupo de jovens da igreja está vendendo lanches para arrecadar dinheiro para participar da convenção. Amy vendeu 2 quilos de doces, 3 caixas de biscoitos e 1 lata de pipoca por um total de vendas de $65. Brian vendeu 4 libras de doces, 6 caixas de biscoitos e 3 latas de pipoca por um total de vendas de $140. Paulina vendeu 8 quilos de doces, 8 caixas de biscoitos e 5 latas de pipoca por um total de vendas de $250. Qual é o custo de cada item?

Resposta: Os doces custam $20; os biscoitos custam $5; e a pipoca custa $10.

14. O fabricante de uma barra de granola gasta $1,20 para fazer cada barra e as vende por $2. O fabricante também tem custos fixos mensais de $8.000.

ⓐ Encontre a função de custo C quando x barras de granola são fabricadas
ⓑ Encontre a função de receita R quando x barras de granola são vendidas.
ⓒ Mostre o ponto de equilíbrio representando graficamente as funções Receita e Custo na mesma grade.
ⓓ Encontre o ponto de equilíbrio. Interprete o que significa o ponto de equilíbrio.

15. Traduza para um sistema de desigualdades e resolva.

Andi não quer gastar mais do que $50 em guloseimas de Halloween. Ela quer comprar barras de chocolate que custam $1 cada e pirulitos que custam $0,50 cada, e ela quer que o número de pirulitos seja pelo menos três vezes o número de barras de chocolate.

ⓐ Escreva um sistema de desigualdades para modelar essa situação.
ⓑ Faça um gráfico do sistema.
ⓒ Ela pode comprar 20 barras de chocolate e 40 pirulitos?

Resposta

ⓐ$\left\{ \begin{array} {l} C\geq 0\\ L\geq 0\\ C+0.5L\leq 50 \\ L\geq 3C \end{array} \right.$
ⓑ

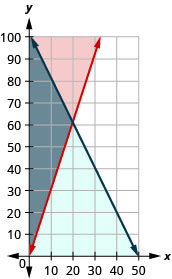
$A figura mostra o gráfico de duas equações. Duas linhas que se cruzam, uma em vermelho e outra em azul, são mostradas. A linha vermelha passa pela origem. Uma área é mostrada em cinza.$

ⓒ não
ⓓ sim