4.8: Representação gráfica de sistemas de desigualdades lineares
- Page ID
- 183233
Ao final desta seção, você poderá:
- Determine se um par ordenado é uma solução de um sistema de desigualdades lineares
- Resolva um sistema de desigualdades lineares representando graficamente
- Resolva aplicações de sistemas de desigualdades
Antes de começar, faça este teste de prontidão.
Determine se um par ordenado é uma solução de um sistema de desigualdades lineares
A definição de um sistema de desigualdades lineares é muito semelhante à definição de um sistema de equações lineares.
Duas ou mais desigualdades lineares agrupadas formam um sistema de desigualdades lineares.
Um sistema de desigualdades lineares parece um sistema de equações lineares, mas tem desigualdades em vez de equações. Um sistema de duas desigualdades lineares é mostrado aqui.
\[\left\{\begin{array} {l} x+4y\geq 10\\3x−2y<12\end{array}\right.\nonumber\]
Para resolver um sistema de desigualdades lineares, encontraremos valores das variáveis que são soluções para ambas as desigualdades. Resolvemos o sistema usando os gráficos de cada desigualdade e mostramos a solução como um gráfico. Encontraremos a região no plano que contém todos os pares ordenados\((x,y)\) que tornam ambas as desigualdades verdadeiras.
As soluções de um sistema de desigualdades lineares são os valores das variáveis que tornam todas as desigualdades verdadeiras.
A solução de um sistema de desigualdades lineares é mostrada como uma região sombreada no sistema de\(xy\) coordenadas -que inclui todos os pontos cujos pares ordenados tornam as desigualdades verdadeiras.
Para determinar se um par ordenado é uma solução para um sistema de duas desigualdades, substituímos os valores das variáveis em cada desigualdade. Se o par ordenado tornar as duas desigualdades verdadeiras, é uma solução para o sistema.
Determine se o par pedido é uma solução para o sistema\(\left\{\begin{array} {l} x+4y\geq 10\\3x−2y<12\end{array}\right.\)
a.\((−2,4)\) b.\((3,1)\)
Solução:
a. O par pedido é\((−2,4)\) uma solução?

O par ordenado\((−2,4)\) tornou as duas desigualdades verdadeiras. Portanto,\((−2,4)\) é uma solução para esse sistema.
b. O par pedido é\((3,1)\) uma solução?

O par ordenado\((3,1)\) tornou uma desigualdade verdadeira, mas a outra falsa. Portanto, não\((3,1)\) é uma solução para este sistema.
Determine se o par pedido é uma solução para o sistema:\(\left\{ \begin{array} {l} x−5y>10\\2x+3y>−2 \end{array} \right.\)
a.\((3,−1)\) b.\((6,−3)\)
- Resposta
-
a. não
b. sim
Determine se o par pedido é uma solução para o sistema:\(\left\{ \begin{array} {l} y>4x−2\\4x−y<20 \end{array} \right.\)
a.\((−2,1)\) b.\((4,−1)\)
- Resposta
-
a. sim
b. não
Resolva um sistema de desigualdades lineares por meio de gráficos
A solução para uma única desigualdade linear é a região em um lado da linha limite que contém todos os pontos que tornam a desigualdade verdadeira. A solução para um sistema de duas desigualdades lineares é uma região que contém as soluções para ambas as desigualdades. Para encontrar essa região, representaremos graficamente cada desigualdade separadamente e, em seguida, localizaremos a região onde ambas são verdadeiras. A solução é sempre mostrada como um gráfico.
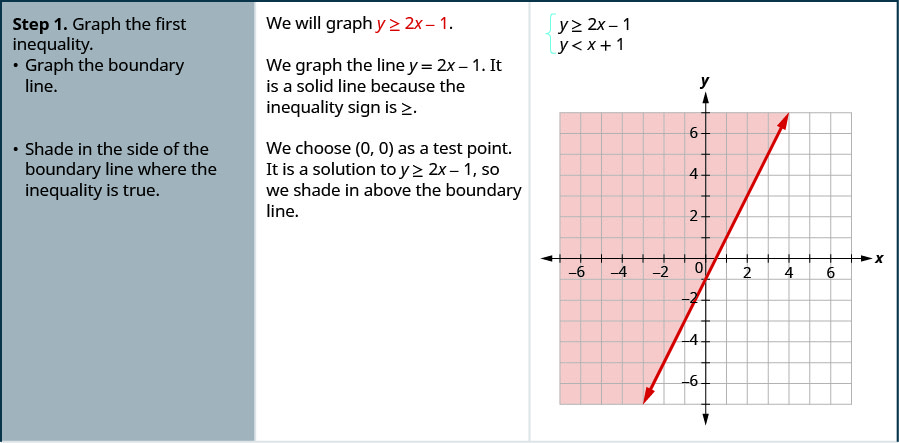
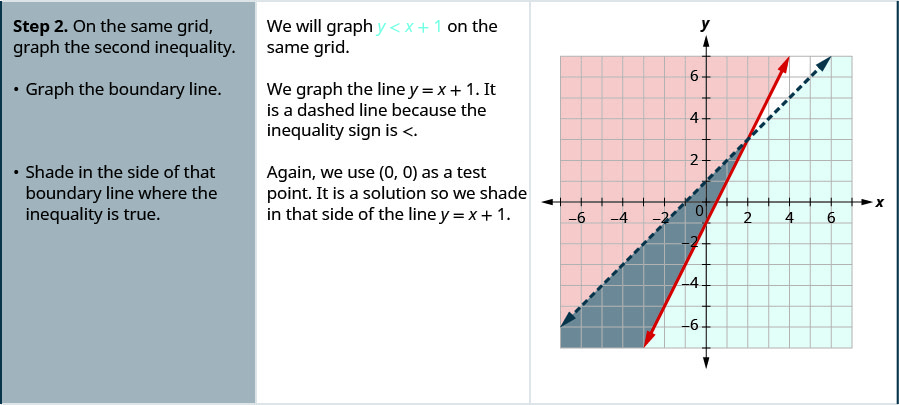
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} y\geq 2x−1 \\ y<x+1\end{array}\right.\)
Solução:


Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} y<3x+2\\y>−x−1\end{array}\right.\)
- Resposta
-
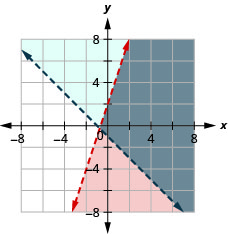
A solução é a região cinza.
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} y<−12x+3 \\ y<3x−4\end{array}\right.\)
- Resposta
-
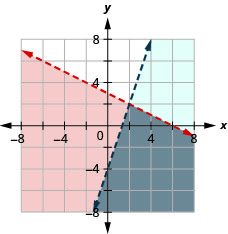
A solução é a região cinza.
- Faça um gráfico da primeira desigualdade.
- Faça um gráfico da linha limite.
- Sombreie o lado da linha limite onde a desigualdade é verdadeira.
- Na mesma grade, represente graficamente a segunda desigualdade.
- Faça um gráfico da linha limite.
- Sombreie o lado dessa linha limite onde a desigualdade é verdadeira.
- A solução é a região onde o sombreamento se sobrepõe.
- Verifique escolhendo um ponto de teste.
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} x−y>3\\y<−15x+4\end{array}\right.\)
Solução:
| \(\left\{\begin{array} {l} x−y>3\\y<−15x+4\end{array}\right.\) | |
| Faça um gráfico\(x - y > 3,\) representando graficamente\(x - y = 3\) e testando um ponto. As interceptações são\(x = 3\) e\(y = −3\) e a linha limite será tracejada. Teste o\((0, 0)\) que torna a desigualdade falsa, então sombreie (vermelho) o lado que não contém\((0, 0).\) |
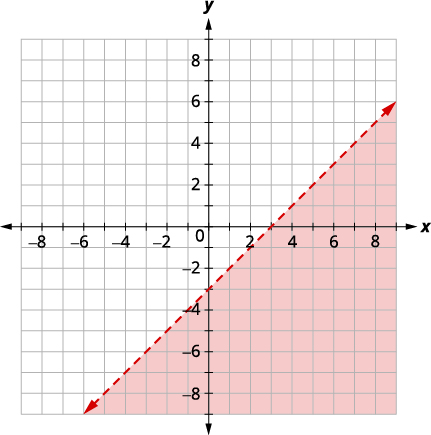 |
| Faça um gráfico\(y<−15x+4\) representando graficamente\(y=−15x+4\) usando a inclinação\(m=−15\) e\(b = 4.\) o\(y\) -intercept A linha limite será tracejada Teste\((0, 0)\) que torna a desigualdade verdadeira, então sombrear (azul) o lado que contém\((0, 0).\) Escolha um ponto de teste na solução e verifique se é uma solução para ambas as desigualdades. |
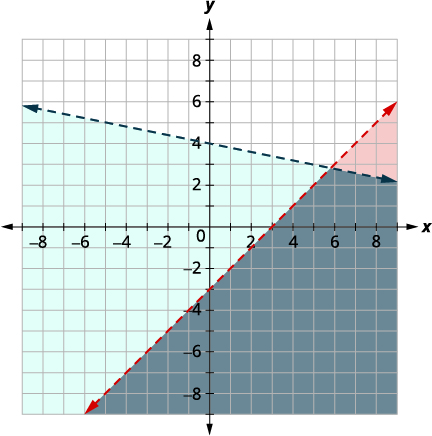 |
O ponto de interseção das duas linhas não está incluído, pois ambas as linhas limite foram tracejadas. A solução é a área sombreada duas vezes, que aparece como a região sombreada mais escura.
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} x+y\leq 2 \\ y\geq \frac{2}{3}x−1\end{array}\right.\)
- Resposta
-
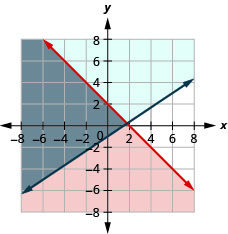
A solução é a região cinza.
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} 3x−2y\leq 6\\y>−\frac{1}{4}x+5\end{array} \right.\)
- Resposta
-
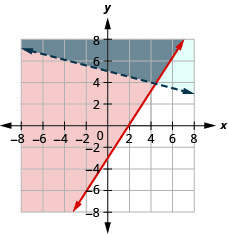
A solução é a região cinza.
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} x−2y<5\\y>−4\end{array}\right.\)
Solução:
| \(\left\{\begin{array} {l} x−2y<5\\y>−4\end{array}\right.\) | |
| Grafe\(x−2y<5\), representando graficamente\(x−2y=5\) e testando um ponto. As interceptações são\(x = 5\) e\(y = −2.5\) e a linha limite será tracejada. Teste o\((0, 0)\) que torna a desigualdade verdadeira, então sombreie (vermelho) o lado que contém\((0, 0).\) |
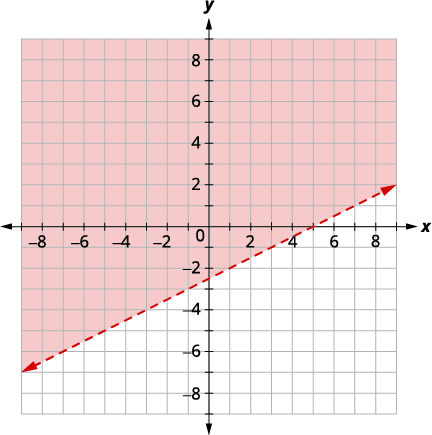 |
| Gráfico\(y>−4\), representando graficamente\(y=−4\) e reconhecendo que é uma linha horizontal\(y=−4\). A linha limite será tracejada. Teste o\((0, 0)\) que torna a desigualdade verdadeira, então sombreie (azul) o lado que contém\((0, 0).\) |
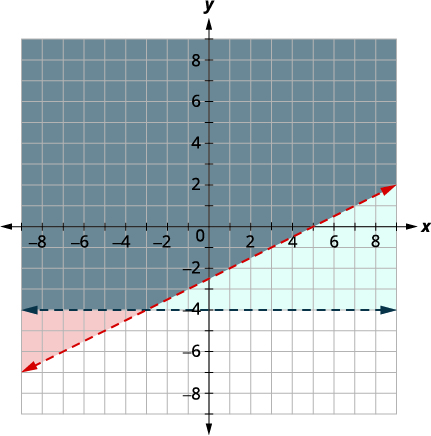 |
A questão\((0,0)\) está na solução e já descobrimos que é uma solução para cada desigualdade. O ponto de interseção das duas linhas não está incluído, pois ambas as linhas limite foram tracejadas.
A solução é a área sombreada duas vezes, que aparece como a região sombreada mais escura.
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} y\geq 3x−2 \\ y<−1\end{array}\right.\)
- Resposta
-
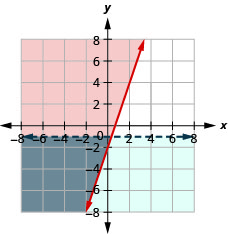
A solução é a região cinza.
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} x>−4x−2 \\ y\geq −4 \end{array}\right.\)
- Resposta
-
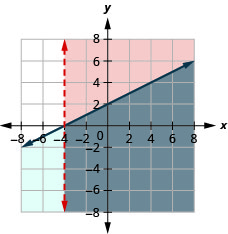
A solução é a região cinza.
Sistemas de desigualdades lineares em que as linhas limite são paralelas podem não ter solução. Veremos isso no próximo exemplo.
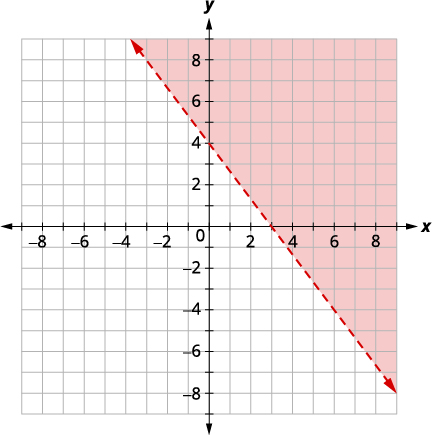
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} 4x+3y\geq 12 \\ y<−\frac{4}{3}x+1\end{array}\right.\)
Solução:
| \(\left\{\begin{array} {l} 4x+3y\geq 12 \\ y<−\frac{4}{3}x+1\end{array}\right.\) | |
| Grafe\(4x+3y\geq 12\), representando graficamente\(4x+3y=12\) e testando um ponto. As interceptações são\(x = 3\) \(y = 4\) e e a linha limite será sólida. Teste o\((0, 0)\) que torna a desigualdade falsa, então sombreie (vermelho) o lado que não contém\((0, 0).\) |
 |
| Faça um gráfico\(y<−\frac{4}{3}x+1\) representando graficamente\(y=−\frac{4}{3}x+1\) usando a inclinação\(m=−\frac{4}{3}\) e\(b = 1.\) o\(y\) -intercept A linha limite será tracejada. Teste o\((0, 0)\) que torna a desigualdade verdadeira, então sombreie (azul) o lado que contém\((0, 0).\) |
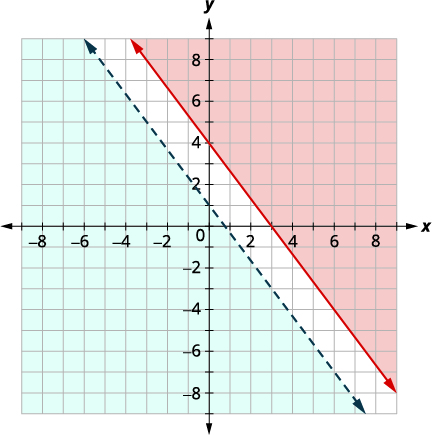 |
Não adianta nas duas regiões sombreadas, então o sistema não tem solução.
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} 3x−2y\geq 12 \\ y\geq \frac{3}{2}x+1\end{array}\right.\)
- Resposta
-
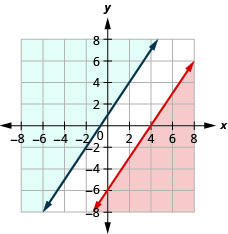
Sem solução.
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} x+3y>8\\y<−\frac{1}{3}x−2\end{array}\right.\)
- Resposta
-
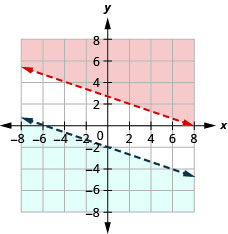
Sem solução.
Alguns sistemas de desigualdades lineares em que as linhas limite são paralelas terão uma solução. Veremos isso no próximo exemplo.
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} y>\frac{1}{2}x−4\\x−2y<−4\end{array}\right.\)
Solução:
| \(\left\{\begin{array} {l} y>\frac{1}{2}x−4\\x−2y<−4\end{array}\right.\) | |
| Faça um gráfico\(y>\frac{1}{2}x−4\) representando graficamente\(y=\frac{1}{2}x−4\) usando a inclinação\(m=\frac{1}{2}\) e\(b = −4.\) o intercepto. A linha limite será tracejada. Teste o\((0, 0)\) que torna a desigualdade verdadeira, então sombreie (vermelho) o lado que contém\((0, 0).\) |
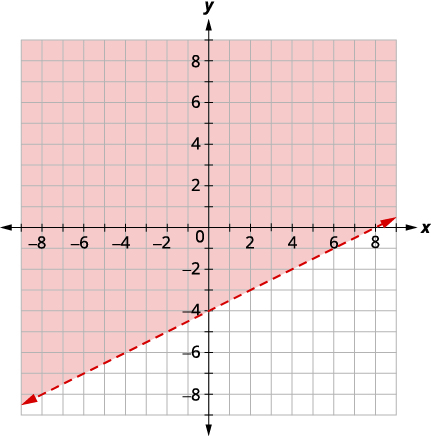 |
| Faça um gráfico\(x−2y<−4\) representando graficamente\(x−2y=−4\) e testando um ponto. As interceptações são\(x = -4\) e\(y=2\) e a linha limite será tracejada. Escolha um ponto de teste na solução e verifique se é uma solução para ambas as desigualdades. Teste o\((0, 0)\) que torna a desigualdade falsa, então sombreie (azul) o lado que não contém\((0, 0).\) |
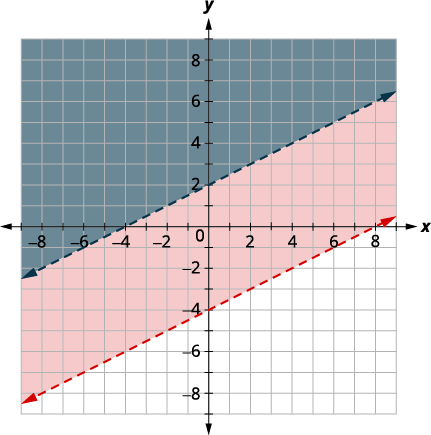 |
Nenhum ponto nas linhas de limite está incluído na solução, pois ambas as linhas são tracejadas.
A solução é a região sombreada duas vezes, que também é a solução para\(x−2y<−4\).
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} y\geq 3x+1 \\ −3x+y\geq −4\end{array}\right.\)
- Resposta
-
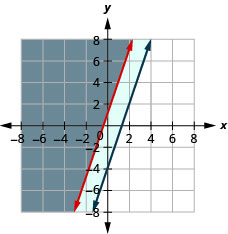
A solução é a região cinza.
Resolva o sistema representando graficamente:\(\left\{\begin{array} {l} y\leq −\frac{1}{4}x+2\\x+4y\leq 4\end{array}\right.\)
- Resposta
-
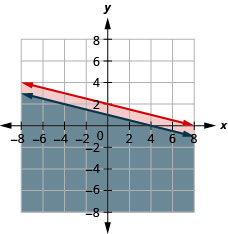
A solução é a região cinza.
Resolva aplicações de sistemas de desigualdades
A primeira coisa que precisaremos fazer para resolver aplicações de sistemas de desigualdades é traduzir cada condição em uma desigualdade. Em seguida, representamos graficamente o sistema, como fizemos acima, para ver a região que contém as soluções. Muitas situações serão realistas somente se ambas as variáveis forem positivas, então adicionamos desigualdades ao sistema como requisitos adicionais.
Christy vende suas fotos em um estande em uma feira de rua. No início do dia, ela quer ter pelo menos 25 fotos para exibir em seu estande. Cada foto pequena que ela exibe custa $4 e cada foto grande custa $10. Ela não quer gastar mais do que $200 em fotos para exibir.
a. Escreva um sistema de desigualdades para modelar essa situação.
b. Faça um gráfico do sistema.
c. Ela poderia exibir 10 fotos pequenas e 20 grandes?
d. Ela poderia exibir 20 fotos grandes e 10 pequenas?
Solução:
uma.
\(\begin{array} {ll} \text{Let} &{x=\text{the number of small photos.}} \\ {} &{y=\text{the number of large photos}}\end{array}\)
Para encontrar o sistema de equações, traduza as informações.
\( \qquad \begin{array} {l} \\ \\ \text{She wants to have at least 25 photos.} \\ \text{The number of small plus the number of large should be at least }25. \\ \hspace{45mm} x+y\geq 25 \\ \\ \\ $4 \text{ for each small and }$10\text{ for each large must be no more than }$200 \\ \hspace{40mm} 4x+10y\leq 200 \\ \\ \\ \text{The number of small photos must be greater than or equal to }0. \\ \hspace{50mm} x\geq 0 \\ \\ \\ \text{The number of large photos must be greater than or equal to }0. \\ \hspace{50mm} y\geq 0 \end{array} \)
Temos nosso sistema de equações.
\(\hspace{65mm} \left\{\begin{array} {l} x+y\geq 25 \\4x+10y\leq 200\\x\geq 0\\y\geq 0\end{array}\right.\)
b.
Como\(x\geq 0\) e\(y\geq 0\) (ambas são maiores ou iguais a), todas as soluções estarão no primeiro quadrante. Como resultado, nosso gráfico mostra apenas o quadrante um.
| Para representar graficamente\(x+y\geq 25\), faça um gráfico\(x+y=25\) como uma linha sólida. Escolha\((0, 0)\) como ponto de teste. Como isso não torna a desigualdade verdadeira, sombreie (vermelho) o lado que não inclui o ponto\((0, 0).\) Para gráfico\(4x+10y\leq 200\), grafe\(4x+10y=200\) como uma linha sólida. Escolha\((0, 0)\) como ponto de teste. Como isso torna a desigualdade verdadeira, sombreie (azul) o lado que inclui o ponto\((0, 0).\) |
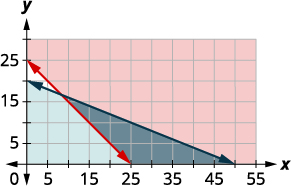 |
A solução do sistema é a região do gráfico mais sombreada. As seções da linha limite que delimitam a seção sombreada de forma escura são incluídas na solução, assim como os pontos no\(x\) eixo -de\((25, 0)\) até\((55, 0).\)
c. Para determinar se 10 fotos pequenas e 20 grandes funcionariam, examinamos o gráfico para ver se o ponto\((10, 20)\) está na região da solução. Também poderíamos testar o ponto para ver se é uma solução de ambas as equações.
Não é, Christy não mostraria 10 fotos pequenas e 20 grandes.
d. Para determinar se 20 fotos pequenas e 10 grandes funcionariam, examinamos o gráfico para ver se o ponto\((20, 10)\) está na região da solução. Também poderíamos testar o ponto para ver se é uma solução de ambas as equações.
É, então Christy poderia escolher exibir 20 fotos pequenas e 10 grandes.
Observe que também podemos testar as soluções possíveis substituindo os valores em cada desigualdade.
Um trailer pode carregar um peso máximo de 160 libras e um volume máximo de 15 pés cúbicos. Um forno de microondas pesa 30 libras e tem 2 pés cúbicos de volume, enquanto uma impressora pesa 20 libras e tem 3 pés cúbicos de espaço.
a. Escreva um sistema de desigualdades para modelar essa situação.
b. Faça um gráfico do sistema.
c. Podem ser transportadas 4 microondas e 2 impressoras neste trailer?
d. 7 microondas e 3 impressoras poderiam ser transportadas neste trailer?
- Resposta
-
a.\(\left\{\begin{array} {l} 30m+20p\leq 160\\2m+3p\leq 15\end{array}\right.\)
b.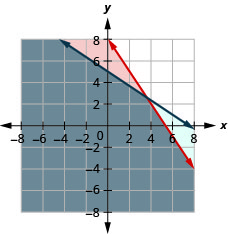
c. sim
d. não
Mary precisa comprar suprimentos de folhas de respostas e lápis para um teste padronizado a ser dado aos juniores de seu ensino médio. O número de folhas de respostas necessárias é pelo menos 5 a mais do que o número de lápis. Os lápis custam $2 e as folhas de respostas custam $1. O orçamento de Mary para esses suprimentos permite um custo máximo de $400.
a. Escreva um sistema de desigualdades para modelar essa situação.
b. Faça um gráfico do sistema.
c. Mary poderia comprar 100 lápis e 100 folhas de respostas?
d. Mary poderia comprar 150 lápis e 150 folhas de respostas?
- Resposta
-
a.\(\left\{\begin{array} {l} a\geq p+5 \\ a+2p\leq 400\end{array}\right.\)
b.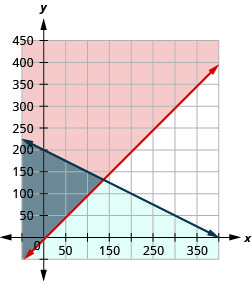
c. não
d. não
Quando usamos variáveis diferentes de\(x\) e\(y\) para definir uma quantidade desconhecida, também devemos alterar os nomes dos eixos do gráfico.
Omar precisa ingerir pelo menos 800 calorias antes de ir para o treino em equipe. Tudo o que ele quer são hambúrgueres e biscoitos, e ele não quer gastar mais do que $5. No restaurante de hambúrguer perto de sua faculdade, cada hambúrguer tem 240 calorias e custa $1,40. Cada biscoito tem 160 calorias e custa $0,50.
a. Escreva um sistema de desigualdades para modelar essa situação.
b. Faça um gráfico do sistema.
c. Ele poderia comer 3 hambúrgueres e 1 biscoito?
d. Ele poderia comer 2 hambúrgueres e 4 biscoitos?
Solução:
uma.
\(\begin{array} {ll} \text{Let} & h=\text{the number of hamburgers.} \\ & c=\text{the number of cookies}\end{array}\)
Para encontrar o sistema de equações, traduza as informações.
As calorias dos hambúrgueres com 240 calorias cada, mais as calorias dos biscoitos com 160 calorias cada, devem ser superiores a 800.
\(\qquad \begin{array} {l} \hspace{40mm} 240h+160c\geq 800 \\ \\ \\ \text{The amount spent on hamburgers at }$1.40\text{ each, plus the amount spent on cookies}\\\text{at }$0.50\text{ each must be no more than }$5.00.\\ \hspace{40mm} 1.40h+0.50c\leq 5 \\ \\ \\ \text{The number of hamburgers must be greater than or equal to 0.} \\ \hspace{50mm} h\geq 0 \\ \text{The number of cookies must be greater than or equal to 0.}\\ \hspace{50mm} c\geq 0 \end{array} \)
\(\text{We have our system of equations.} \qquad \left\{ \begin{array} {l} 240h+160c\geq 800 \\ 1.40h+0.50c\leq 5 \\ h\geq 0 \\ c\geq 0\end{array} \right.\)
b.
Como\(h\geq 0\) e\(c\geq 0\) (ambas são maiores ou iguais a), todas as soluções estarão no primeiro quadrante. Como resultado, nosso gráfico mostra apenas o quadrante um.
| Para representar graficamente\(240h+160c\geq 800\), faça um gráfico\(240h+160c=800\) como uma linha sólida. Escolha\((0, 0)\) como ponto de teste. Como isso não torna a desigualdade verdadeira, sombreie (vermelho) o lado que não inclui o ponto\((0, 0).\) |
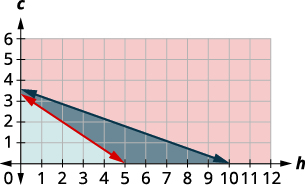 |
Gráfico\(1.40h+0.50c\leq 5\). A linha limite é\(1.40h+0.50c=5\). Nós testamos\((0, 0)\) e isso torna a desigualdade verdadeira. Sombreamos o lado da linha que inclui\((0, 0).\)
A solução do sistema é a região do gráfico mais sombreada. As seções da linha limite que delimitam a seção sombreada de forma escura são incluídas na solução, assim como os pontos no\(x\) eixo -de\((5, 0)\) até\((10, 0).\)
c. Para determinar se 3 hambúrgueres e 2 biscoitos atenderiam aos critérios de Omar, vemos se o ponto\((3, 2)\) está na região da solução. É, então Omar pode escolher comer 3 hambúrgueres e 2 biscoitos.
d. Para determinar se 2 hambúrgueres e 4 biscoitos atenderiam aos critérios de Omar, vemos se o ponto\((2, 4)\) está na região da solução. Ou seja, Omar pode optar por comer 2 hambúrgueres e 4 biscoitos.
Também poderíamos testar as soluções possíveis substituindo os valores em cada desigualdade.
A tensão precisa ingerir pelo menos 1.000 calorias extras por dia para se preparar para correr uma maratona. Ele tem apenas $25 para gastar com a comida extra de que precisa e vai gastá-la em donuts de $0,75 com 360 calorias cada e $2 em bebidas energéticas com 110 calorias.
a. Escreva um sistema de desigualdades que modele essa situação.
b. Faça um gráfico do sistema.
c. Ele pode comprar 8 donuts e 4 bebidas energéticas e satisfazer suas necessidades calóricas?
d. Ele pode comprar 1 donut e 3 bebidas energéticas e satisfazer suas necessidades calóricas?
- Resposta
-
a.\(\left\{\begin{array} {l} 0.75d+2e\leq 25\\360d+110e\geq 1000\end{array}\right.\)
b.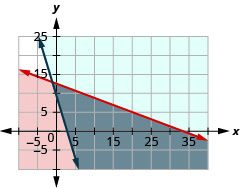
c. sim
d. não
O médico de Philip diz que ele deve adicionar pelo menos 1.000 calorias a mais por dia à sua dieta habitual. Philip quer comprar barras de proteína que custam $1,80 cada e têm 140 calorias e suco que custa $1,25 por garrafa e tem 125 calorias. Ele não quer gastar mais do que $12.
a. Escreva um sistema de desigualdades que modele essa situação.
b. Faça um gráfico do sistema.
c. Ele pode comprar 3 barras de proteína e 5 garrafas de suco?
d. Ele pode comprar 5 barras de proteína e 3 garrafas de suco?
- Resposta
-
a.\(\left\{\begin{array} {l} 140p+125j\geq 1000\\1.80p+1.25j\leq 12\end{array}\right.\)
b.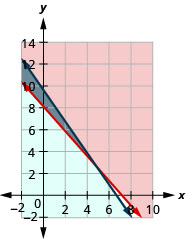
c. sim
d. não
Acesse esses recursos on-line para obter instruções e práticas adicionais na resolução de sistemas de desigualdades lineares por meio de gráficos.
- Resolvendo sistemas de desigualdades lineares por meio de gráficos
- Sistemas de desigualdades lineares
Conceitos-chave
- Soluções de um sistema de desigualdades lineares: As soluções de um sistema de desigualdades lineares são os valores das variáveis que tornam todas as desigualdades verdadeiras. A solução de um sistema de desigualdades lineares é mostrada como uma região sombreada no sistema de\(xy\) coordenadas -que inclui todos os pontos cujos pares ordenados tornam as desigualdades verdadeiras.
- Como resolver um sistema de desigualdades lineares por meio de gráficos.
- Faça um gráfico da primeira desigualdade.
Faça um gráfico da linha limite.
Sombreie o lado da linha limite onde a desigualdade é verdadeira. - Na mesma grade, represente graficamente a segunda desigualdade.
Faça um gráfico da linha limite.
Sombreie o lado dessa linha limite onde a desigualdade é verdadeira. - A solução é a região onde o sombreamento se sobrepõe.
- Verifique escolhendo um ponto de teste.
- Faça um gráfico da primeira desigualdade.
Glossário
- sistema de desigualdades lineares
- Duas ou mais desigualdades lineares agrupadas formam um sistema de desigualdades lineares.


