4.7E: Exercícios

Last updated
Save as PDF

Page ID: 183216

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A prática leva à perfeição

Avalie o determinante de uma matriz 2 × 2

Nos exercícios a seguir, avalie a determinação de cada matriz quadrada.

$\left[\begin{matrix}6&−2\\3&−1\end{matrix}\right]$

$\left[\begin{matrix}−4&8\\−3&5\end{matrix}\right]$

Resposta: $4$

$\left[\begin{matrix}−3&5\\0&−4\end{matrix}\right]$

$\left[\begin{matrix}−2&0\\7&−5\end{matrix}\right]$

Resposta: $10$

Avalie o determinante de uma matriz 3 × 3

Nos exercícios a seguir, encontre e avalie os menores indicados.

$\left|\begin{matrix}3&−1&4\\−1&0&−2\\−4&1&5\end{matrix}\right|$

Encontre o menor ⓐ$a_1$ ⓑ$b_2$ ⓒ$c_3$

$\left|\begin{matrix}−1&−3&2\\4&−2&−1\\−2&0&−3\end{matrix}\right|$

Encontre o menor ⓐ$a_1$ ⓑ$b_1$ ⓒ$c_2$

Resposta: ⓐ 6 ⓑ$−14$ ⓒ$−6$

$\left|\begin{matrix}2&−3&−4\\−1&2&−3\\0&−1&−2\end{matrix}\right|$

Encontre o menor ⓐ$a_2$ ⓑ$b_2$ ⓒ$c_2$

$\left|\begin{matrix}−2&−2&3\\1&−3&0\\−2&3&−2\end{matrix}\right|$

Encontre o menor ⓐ$a_3$ ⓑ$b_3$ ⓒ$c_3$

Resposta: ⓐ 9 ⓑ$−3$ ⓒ 8

Nos exercícios a seguir, avalie cada determinante expandindo por menores ao longo da primeira linha.

$\left|\begin{matrix}−2&3&−1\\−1&2&−2\\3&1&−3\end{matrix}\right|$

$\left|\begin{matrix}4&−1&−2\\−3&−2&1\\−2&−5&7\end{matrix}\right|$

Resposta: $−77$

$\left|\begin{matrix}−2&−3&−4\\5&−6&7\\−1&2&0\end{matrix}\right|$

$\left|\begin{matrix}1&3&−2\\5&−6&4\\0&−2&−1\end{matrix}\right|$

Responda: $49$

Nos exercícios a seguir, avalie cada determinante por meio da expansão por menores.

$\left|\begin{matrix}−5&−1&−4\\4&0&−3\\2&−2&6\end{matrix}\right|$

$\left|\begin{matrix}4&−1&3\\3&−2&2\\−1&0&4\end{matrix}\right|$

Responda: $−24$

$\left|\begin{matrix}3&5&4\\−1&3&0\\−2&6&1\end{matrix}\right|$

$\left|\begin{matrix}2&−4&−3\\5&−1&−4\\3&2&0\end{matrix}\right|$

Responda: $25$

Use a regra de Cramer para resolver sistemas de equações

Nos exercícios a seguir, resolva cada sistema de equações usando a Regra de Cramer.

$\left\{\begin{array} {l} −2x+3y=3\\x+3y=12\end{array}\right.$

$\left\{\begin{array} {l} x−2y=−5\\2x−3y=−4\end{array}\right.$

Responda: $(7,6)$

$\left\{\begin{array} {l} x−3y=−9\\2x+5y=4\end{array}\right.$

$\left\{\begin{array} {l} 2x+y=−4\\3x−2y=−6\end{array}\right.$

Responda: $(−2,0)$

$\left\{\begin{array} {l} x−2y=−5\\2x−3y=−4\end{array}\right.$

$\left\{\begin{array} {l} x−3y=−9\\2x+5y=4\end{array}\right.$

Responda: $(−3,2)$

$\left\{\begin{array} {l} 5x−3y=−1\\2x−y=2\end{array}\right.$

$\left\{\begin{array} {l} 3x+8y=−3\\2x+5y=−3\end{array}\right.$

Responda: $(−9,3)$

$\left\{\begin{array} {l} 6x−5y+2z=3\\2x+y−4z=5\\3x−3y+z=−1 \end{array}\right.$

$\left\{\begin{array} {l} 4x−3y+z=7\\2x−5y−4z=3\\3x−2y−2z=−7\end{array}\right.$

Responda: $(−3,−5,4)$

$\left\{\begin{array} {l} 2x−5y+3z=8\\3x−y+4z=7\\x+3y+2z=−3\end{array}\right.$

$\left\{\begin{array} {l} 11x+9y+2z=−9\\7x+5y+3z=−7\\4x+3y+z=−3\end{array}\right.$

Responda: $(2,−3,−2)$

$\left\{\begin{array} {l} x+2z=0\\4y+3z=−2\\2x−5y=3\end{array}\right.$

$\left\{\begin{array} {l} 2x+5y=4\\3y−z=3\\4x+3z=−3\end{array}\right.$

Responda: $(−3,2,3)$

$\left\{\begin{array} {l} 2y+3z=−1\\5x+3y=−6\\7x+z=1\end{array}\right.$

$\left\{\begin{array} {l} 3x−z=−3\\5y+2z=−6\\4x+3y=−8\end{array}\right.$

Responda: $(−2,0,−3)$

$\left\{\begin{array} {l} 2x+y=3\\6x+3y=9\end{array}\right.$

$\left\{\begin{array} {l} x−4y=−1\\−3x+12y=3\end{array}\right.$

Responda: infinitas soluções

$\left\{\begin{array} {l} −3x−y=4\\6x+2y=−16\end{array}\right.$

$\left\{\begin{array} {l} 4x+3y=2\\20x+15y=5\end{array}\right.$

Responda: inconsistentes

$\left\{\begin{array} {l} x+y−3z=−1\\y−z=0\\−x+2y=1\end{array}\right.$

$\left\{\begin{array} {l} 2x+3y+z=1\\2x+y+z=9\\3x+4y+2z=20\end{array}\right.$

Responda: inconsistentes

$\left\{\begin{array} {l} 3x+4y−3z=−2\\2x+3y−z=−1\\2x+y−2z=6\end{array}\right.$

$\left\{\begin{array} {l} x−2y+3z=1\\x+y−3z=7\\3x−4y+5z=7\end{array}\right.$

Responda: infinitas soluções

Resolva aplicativos usando determinantes

Nos exercícios a seguir, determine se os pontos fornecidos são colineares.

$(0,1)$,$(2,0)$,$(−2,2)$ e.

$(0,−5)$,$(−2,−2)$,$(2,−8)$ e.

Responda: sim

$(4,−3)$,$(6,−4)$,$(2,−2)$ e.

$(−2,1)$,$(−4,4)$,$(0,−2)$ e.

Responda: não

exercícios de escrita

Explique a diferença entre uma matriz quadrada e seu determinante. Dê um exemplo de cada um.

Explique o que significa o menor de uma entrada em uma matriz quadrada.

Responda: As respostas podem variar.

Explique como decidir qual linha ou coluna você usará para expandir um$3×3$ determinante.

Explique as etapas para resolver um sistema de equações usando a regra de Cramer.

Responda: As respostas podem variar.

Verificação automática

ⓐ Depois de concluir os exercícios, use esta lista de verificação para avaliar seu domínio dos objetivos desta seção.

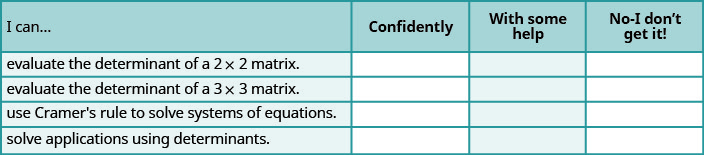
$Essa tabela tem 4 colunas, 4 linhas e uma linha de cabeçalho. A linha do cabeçalho rotula cada coluna: eu posso, com confiança, com alguma ajuda e não, eu não entendo. A primeira coluna tem as seguintes afirmações: Avalie o determinante de uma matriz 2 por 2, avalie o determinante de uma matriz 3 por 3, use a regra de Cramer para resolver sistemas de equações, resolver aplicações usando determinantes. As colunas restantes estão em branco.$

ⓑ Depois de revisar essa lista de verificação, o que você fará para se tornar confiante em todos os objetivos?