4.7: Resolver sistemas de equações usando determinantes
- Page ID
- 183202
Ao final desta seção, você poderá:
- Avalie o determinante de uma matriz 2×2
- Avalie o determinante de uma matriz 3×3
- Use a Regra de Cramer para resolver sistemas de equações
- Resolva aplicativos usando determinantes
Antes de começar, faça este teste de prontidão.
Nesta seção, aprenderemos sobre outro método para resolver sistemas de equações lineares chamado regra de Cramer. Antes de começarmos a usar a regra, precisamos aprender algumas novas definições e notações.
Avalie o determinante de uma\(2×2\) matriz
Se uma matriz tem o mesmo número de linhas e colunas, nós a chamamos de matriz quadrada. Cada matriz quadrada tem um número real associado a ela chamado de determinante. Para encontrar o determinante da matriz quadrada\(\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] \), primeiro a escrevemos como\(\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| \). Para obter o valor do número real do determinado, subtraímos os produtos das diagonais, conforme mostrado.
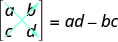
O determinante de qualquer matriz quadrada\(\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] \), onde a, b, c e d são números reais, é
\[\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| =ad−bc \nonumber \]
Avalie a determinação de ⓐ\(\left[ \begin{matrix} 4 &-2 \\ 3&-1 \end{matrix} \right] \) ⓑ\(\left[ \begin{matrix} -3 &-4 \\ -2&0 \end{matrix} \right] \).
- Responda
-
ⓐ

Escreva o determinante. 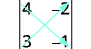
Subtraia os produtos das diagonais. 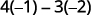
Simplifique. 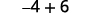
Simplifique. 
ⓑ
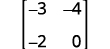
Escreva o determinante. 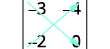
Subtraia os produtos das diagonais. 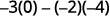
Simplifique. 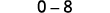
Simplifique. 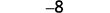
Avalie a determinação de ⓐ\(\left[ \begin{matrix} 5&−3\\2&−4 \end{matrix} \right] \) ⓑ\(\left[ \begin{matrix} −4&−6\\0&7 \end{matrix} \right] \).
- Responda
-
ⓐ\(−14\); ⓑ\(−28\)
Avalie a determinação de ⓐ\(\left[ \begin{matrix} −1&3\\−2&4 \end{matrix} \right] \) ⓑ\(\left[ \begin{matrix} −7&−3\\−5&0 \end{matrix} \right] \).
- Responda
-
ⓐ 2 ⓑ\(−15\)
Avalie o determinante de uma\(3×3\) matriz
Para avaliar o determinante de uma\(3×3\) matriz, temos que ser capazes de avaliar o menor de uma entrada no determinante. O menor de uma entrada é o\(2×2\) determinante encontrado ao eliminar a linha e a coluna no\(3×3\) determinante que contém a entrada.
O menor de uma entrada em um\(3×3\) determinante é o\(2×2\) determinante encontrado ao eliminar a linha e a coluna no\(3×3\) determinante que contém a entrada.
Para encontrar a menor entrada\(a_1\), eliminamos a linha e a coluna que a contêm. Então, eliminamos a primeira linha e a primeira coluna. Em seguida, escrevemos o\(2×2\) determinante que permanece.

Para encontrar a menor entrada\(b_2\), eliminamos a linha e a coluna que a contêm. Então, eliminamos a\(2^{nd}\) linha e a\(2^{nd}\) coluna. Em seguida, escrevemos o\(2×2\) determinante que permanece.

Para o determinante\(\left| \begin{matrix} 4&−2&3\\1&0&−3\\−2&−4&2 \end{matrix} \right|\), encontre e depois avalie o menor de ⓐ\(a_1\) ⓑ\(b_3\) ⓒ\(c_2\).
- Responda
-
ⓐ
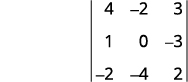
Elimine a linha e a coluna que contém\(a_1\). 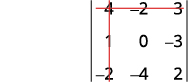
Escreva o\(2×2\) determinante que resta. 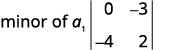
Avalie. 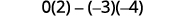
Simplifique. 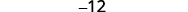
ⓑ
Elimine a linha e a coluna que contém\(b_3\). 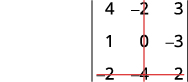
Escreva o\(2×2\) determinante que resta. 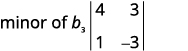
Avalie. 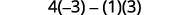
Simplifique. 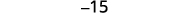
ⓒ
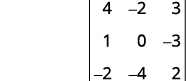
Elimine a linha e a coluna que contém\(c_2\). 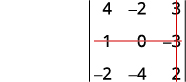
Escreva o\(2×2\) determinante que resta. 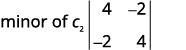
Avalie. 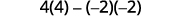
Simplifique. 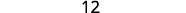
Para o determinante\(\left| \begin{matrix} 1&−1&4\\0&2&−1\\−2&−3&3 \end{matrix} \right|\), encontre e depois avalie o menor de ⓐ\(a_1\) ⓑ\(b_2\) ⓒ\(c_3\).
- Responda
-
ⓐ 3 ⓑ 11 ⓒ 2
Para o determinante\(\left| \begin{matrix} −2&−1&0\\3&0&−1\\−1&−2&3 \end{matrix} \right|\), encontre e depois avalie o menor de ⓐ\(a_2\) ⓑ\(b_3\) ⓒ\(c_2\).
- Responda
-
ⓐ\(−3\) ⓑ 2 ⓒ 3
Agora estamos prontos para avaliar um\(3×3\) determinante. Para fazer isso, expandimos o número de menores, o que nos permite avaliar o\(3×3\)\(2×2\) determinante usando determinantes — que já sabemos como avaliar!
Para avaliar um\(3×3\) determinante expandindo por menores ao longo da primeira linha, usamos o seguinte padrão:
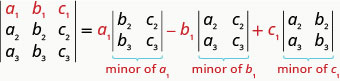
Lembre-se de que, para encontrar o menor de uma entrada, eliminamos a linha e a coluna que contém a entrada.
Para avaliar um\(3×3\) determinante expandindo por menores ao longo da primeira linha, o seguinte padrão:
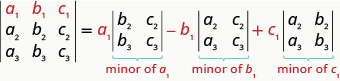
Avalie o determinante expandindo\(\left| \begin{matrix} 2&−3&−1\\3&2&0\\−1&−1&−2 \end{matrix} \right|\) por menores ao longo da primeira linha.
- Responda
-

Expandir por menores ao longo da primeira linha 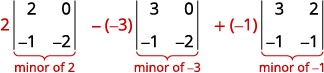
Avalie cada determinante. 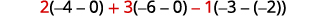
Simplifique. 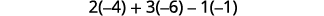
Simplifique. 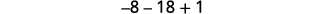
Simplifique. 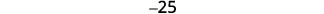
Avalie o determinante\(\left| \begin{matrix} 3&−2&4\\0&−1&−2\\2&3&−1 \end{matrix} \right|\), expandindo por menores ao longo da primeira linha.
- Responda
-
37
Avalie o determinante\(\left| \begin{matrix} 3&−2&−2\\2&−1&4\\−1&0&−3 \end{matrix} \right|\), expandindo por menores ao longo da primeira linha.
- Responda
-
7
Para avaliar um\(3×3\) determinante, podemos expandir por menores usando qualquer linha ou coluna. Escolher uma linha ou coluna diferente da primeira linha às vezes facilita o trabalho.
Quando expandimos em qualquer linha ou coluna, devemos ter cuidado com o sinal dos termos na expansão. Para determinar o sinal dos termos, usamos o seguinte gráfico de padrão de sinais.
\[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]
Ao expandir por menores usando uma linha ou coluna, o sinal dos termos na expansão segue o seguinte padrão. \[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]
Observe que o padrão do sinal na primeira linha corresponde aos sinais entre os termos na expansão pela primeira linha.
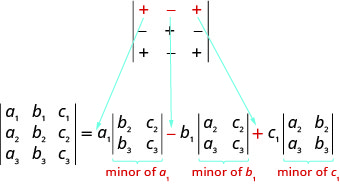
Como podemos expandir em qualquer linha ou coluna, como decidimos qual linha ou coluna usar? Normalmente, tentamos escolher uma linha ou coluna que facilitará nosso cálculo. Se o determinante contiver um 0, usar a linha ou coluna que contém o 0 facilitará os cálculos.
Avalie o determinante\(\left| \begin{matrix} 4&−1&−3\\3&0&2\\5&−4&−3 \end{matrix} \right|\) por meio da expansão por menores.
- Responda
-
Para expandir por menores, procuramos uma linha ou coluna que facilitará nossos cálculos. Como 0 está na segunda linha e na segunda coluna, expandir por qualquer uma delas é uma boa escolha. Como a segunda linha tem menos negativos do que a segunda coluna, expandiremos pela segunda linha.

Expanda usando a segunda linha. Tenha cuidado com os sinais. 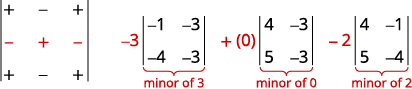
Avalie cada determinante. 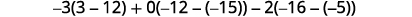
Simplifique. 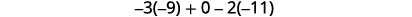
Simplifique. 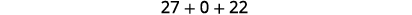
Adicionar. 
Avalie o determinante\(\left| \begin{matrix} 2&−1&−3\\0&3&−4\\3&−4&−3 \end{matrix} \right|\) por meio da expansão por menores.
- Resposta
-
\(−11\)
Avalie o determinante\(\left| \begin{matrix} −2&−1&−3\\−1&2&2\\4&−4&0 \end{matrix} \right|\) por meio da expansão por menores.
- Resposta
-
8
Use a regra de Cramer para resolver sistemas de equações
A Regra de Cramer é um método de resolver sistemas de equações usando determinantes. Ele pode ser derivado resolvendo a forma geral dos sistemas de equações por eliminação. Aqui vamos demonstrar a regra para ambos os sistemas de duas equações com duas variáveis e para sistemas de três equações com três variáveis.
Vamos começar com os sistemas de duas equações com duas variáveis.
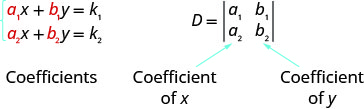
Para o sistema de equações\(\left\{\begin{array} {l} a_1x+b_1y=k_1 \\ a_2x+b_2y=k_2\end{array}\right.\), a solução\((x,y)\) pode ser determinada por

Observe que para formar o determinante D, usamos os coeficientes das variáveis.
Observe que, para formar o determinante\(D_x\)\(D_y\), substituímos as constantes pelos coeficientes da variável que estamos encontrando.
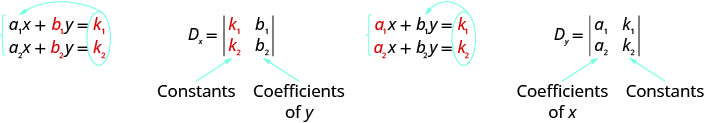
Resolva usando a regra de Cramer:\(\left\{ \begin{array} {l} 2x+y=−4\\3x−2y=−6\end{array}\right.\)
- Resposta
-






Resolva usando a regra de Cramer:\(\left\{\begin{array} {l} 3x+y=−3 \\ 2x+3y=6 \end{array} \right.\)
- Resposta
-
\((−\frac{15}{7},\frac{24}{7})\)
Resolva usando a regra de Cramer:\(\left\{\begin{array} {l} −x+y=2\\2x+y=−4 \end{array} \right.\)
- Resposta
-
\((−2,0)\)
- Avalie o determinante D, usando os coeficientes das variáveis.
- Avalie o determinante\(D_x\). Use as constantes no lugar dos coeficientes x.
- Avalie o determinante\(D_y\). Use as constantes no lugar dos coeficientes y.
- Encontre x e y. \(x=\frac{D_x}{D}\),\(y=\frac{D_y}{D}\)
- Escreva a solução como um par ordenado.
- Verifique se o par ordenado é uma solução para ambas as equações originais.
Para resolver um sistema de três equações com três variáveis com a Regra de Cramer, basicamente fazemos o que fizemos para um sistema de duas equações. No entanto, agora temos que resolver três variáveis para obter a solução. Os determinantes também serão os\(3×3\) que tornarão nosso trabalho mais interessante!
Para o sistema de equações\(\left\{\begin{array} {l} a_1x+b_1y+c_1z=k_1\\a_2x+b_2y+c_2z=k_2\\a_3x+b_3y+c_3z=k_3\end{array}\right.\), a solução\((x,y,z)\) pode ser determinada por

Resolva o sistema de equações usando a Regra de Cramer:\(\left\{\begin{array} {l} 3x−5y+4z=5\\5x+2y+z=0\\2x+3y−2z=3 \end{array} \right.\)
- Resposta
-
Avalie o determinante D. 
Expanda por menores usando a coluna 1. 
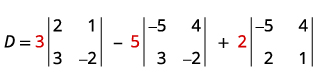
Avalie os determinantes. 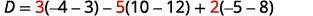
Simplifique. 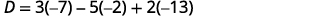
Simplifique. 
Simplifique. 
Avalie o determinante\(D_x\). Use as
constantes para substituir os coeficientes de x.
Expanda por menores usando a coluna 1. 
Avalie os determinantes. 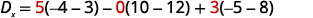
Simplifique. 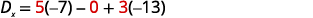
Simplifique. 
Avalie o determinante Dy.Dy. Use as
constantes para substituir os coeficientes de y.

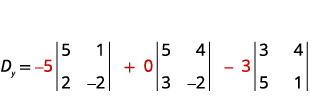
Avalie os determinantes. 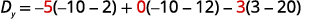
Simplifique. 
Simplifique. 
Simplifique. 
Avalie o determinante Dz.Dz. Use as
constantes para substituir os coeficientes de z.

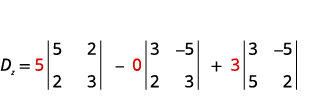
Avalie os determinantes. 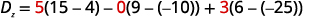
Simplifique. 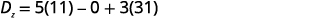
Simplifique. 
Simplifique. 
Encontre x, y e z. 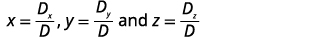
Substitua os valores. 
Simplifique. 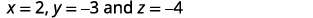
Escreva a solução como uma tripla ordenada. 
Verifique se o triplo ordenado é uma solução
para todas as três equações originais.Deixamos o cheque para você. A solução é\((2,−3,−4)\).
Resolva o sistema de equações usando a Regra de Cramer:\(\left\{\begin{array} {l} 3x+8y+2z=−5\\2x+5y−3z=0\\x+2y−2z=−1 \end{array} \right.\)
- Resposta
-
\((−9,3,−1)\)
Resolva o sistema de equações usando a Regra de Cramer:\(\left\{\begin{array} {l} 3x+y−6z=−3\\2x+6y+3z=0\\3x+2y−3z=−6 \end{array} \right.\)
- Resposta
-
\((−6,3,−2)\)
A regra de Cramer não funciona quando o valor do determinante D é 0, pois isso significaria que estaríamos dividindo por 0. Mas quando\(D=0\), o sistema é inconsistente ou dependente.
Quando os valores de\(D=0\) e\(D_x,\space D_y\) e D são todos zero, o sistema é consistente e dependente e há infinitas soluções.
Quando os valores de\(D=0\) e\(D_x,\space D_y\) e e não\(D_z\) são todos zero, o sistema é inconsistente e não há solução.
Para qualquer sistema de equações, onde o valor do determinante\(D=0\),
\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]
No próximo exemplo, usaremos os valores dos determinantes para encontrar a solução do sistema.
Resolva o sistema de equações usando a regra de Cramer:\(\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.\)
- Resposta
-
\(\begin{array} {ll} {} &{\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.} \\ {\begin{array} {l} \text{Evaluate the determinantD,using the} \\ \text{coefficients of the variables.} \end{array}} &{D=\left|\begin{matrix} 1&3\\−2&−6\end{matrix}\right|} \\ {} &{D=−6−(−6)} \\ {} &{D=0} \end{array} \)
Não podemos usar a Regra de Cramer para resolver esse sistema. Mas, analisando o valor dos determinantes\(D_x\)\(D_y\), podemos determinar se o sistema é dependente ou inconsistente.
\(\begin{array} {ll} {\text{Evaluate the determinant }D_x.} &{D_x=\left|\begin{matrix} 4&3\\3&−6\end{matrix}\right|} \\ {} &{D_x=−24−9} \\ {} &{D_x=15} \end{array} \)
Como nem todos os determinantes são zero, o sistema é inconsistente. Não há solução.
Resolva o sistema de equações usando a regra de Cramer:\(\left\{\begin{array} {l} 4x−3y=8\\8x−6y=14 \end{array} \right.\)
- Resposta
-
sem solução
Resolva o sistema de equações usando a regra de Cramer:\(\left\{\begin{array} {l} x=−3y+4\\2x+6y=8 \end{array} \right.\)
- Resposta
-
soluções infinitas
Resolva aplicativos usando determinantes
Uma aplicação interessante de determinantes nos permite testar se os pontos são colineares. Três pontos\((x_1,y_1)\)\((x_2,y_2)\) e\((x_3,y_3)\) são colineares se e somente se o determinante abaixo for zero.
\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]
Três pontos\((x_1,y_1)\),\((x_2,y_2)\) e\((x_3,y_3)\) são colineares se e somente se
\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]
Usaremos essa propriedade no próximo exemplo.
Determine se os pontos\((5,−5)\)\((4,−3)\), e\((3,−1)\) são colineares.
- Resposta
-
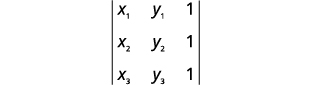
Substitua os valores pelo determinante.
\((5,−5)\),\((4,−3)\), e\((3,−1)\)
Avalie o determinante expandindo
por menores usando a coluna 3.
Avalie os determinantes. 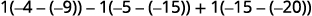
Simplifique. 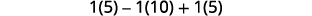
Simplifique. 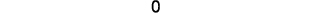
O valor do determinado é 0, então os
pontos são colineares.
Determine se os pontos\((3,−2)\)\((5,−3)\), e\((1,−1)\) são colineares.
- Resposta
-
sim
Determine se os pontos\((−4,−1)\)\((−6,2)\), e\((−2,−4)\) são colineares.
- Resposta
-
sim
Acesse esses recursos on-line para obter instruções e práticas adicionais na resolução de sistemas de desigualdades lineares por meio de gráficos.
- Resolvendo sistemas de desigualdades lineares por meio de gráficos
- Sistemas de desigualdades lineares
Conceitos-chave
- Determinante: O determinante de qualquer matriz quadrada\(\left[\begin{matrix}a&b\\c&d\end{matrix}\right]\), onde a, b, c e d são números reais, é
\[\left|\begin{matrix}a&b\\c&d\end{matrix}\right|=ad−bc\nonumber\]
- Expansão por menores ao longo da primeira linha para avaliar um determinante 3 × 3: Para avaliar um\(3×3\) determinante expandindo por menores ao longo da primeira linha, o seguinte padrão:
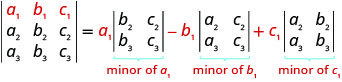
- Padrão de sinal: Ao expandir por menores usando uma linha ou coluna, o sinal dos termos na expansão segue o seguinte padrão.
\[\left|\begin{matrix}+&−&+\\−&+&−\\+&−&+\end{matrix}\right|\nonumber\]
- Regra de Cramer: Para o sistema de equações\(\left\{\begin{array} {l} a_1x+b_1y=k_1\\a_2x+b_2y=k_2\end{array}\right.\), a solução\((x,y)\) pode ser determinada pelo

Aviso de que, para formar o determinante D, usamos os coeficientes das variáveis. - Como resolver um sistema de duas equações usando a regra de Cramer.
- Avalie o determinante D, usando os coeficientes das variáveis.
- Avalie o determinante\(D_x\). Use as constantes no lugar dos coeficientes x.
- Avalie o determinante\(D_y\). Use as constantes no lugar dos coeficientes y.
- Encontre x e y. \(x=\frac{D_x}{D}\),\(y=\frac{D_y}{D}\).
- Escreva a solução como um par ordenado.
- Verifique se o par ordenado é uma solução para ambas as equações originais.
- Sistemas de equações dependentes e inconsistentes: Para qualquer sistema de equações, onde o valor do determinante\(D=0\),\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]
- Teste para pontos colineares: três pontos\((x_1,y_1)\),\((x_2,y_2)\), e\((x_3,y_3)\) são colineares se e somente se
\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]
Glossário
- determinante
- Cada matriz quadrada tem um número real associado a ela chamado de determinante.
- menor de uma entrada em um determinante 3 × 33 × 3
- O menor de uma entrada em um determinante 3 × 33 × 3 é o determinante 2 × 22 × 2 encontrado pela eliminação da linha e da coluna no determinante 3 × 33 × 3 que contém a entrada.
- matriz quadrada
- Uma matriz quadrada é uma matriz com o mesmo número de linhas e colunas.


