4.6: Resolva sistemas de equações usando matrizes

Last updated
Save as PDF

Page ID: 183143

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Ao final desta seção, você poderá:

Escreva a matriz aumentada para um sistema de equações
Use operações de linha em uma matriz
Resolva sistemas de equações usando matrizes

Antes de começar, faça este teste de prontidão.

Resolver:$3(x+2)+4=4(2x−1)+9$.
Se você perdeu esse problema, revise [link].
Resolver:$0.25p+0.25(x+4)=5.20$.
Se você perdeu esse problema, revise [link].
Avalie quando$x=−2$$y=3:2x^2−xy+3y^2$ e.
Se você perdeu esse problema, revise [link].

Escreva a matriz aumentada para um sistema de equações

Resolver um sistema de equações pode ser uma operação tediosa em que um simples erro pode causar estragos na busca da solução. Um método alternativo que usa os procedimentos básicos de eliminação, mas com uma notação mais simples, está disponível. O método envolve o uso de uma matriz. Uma matriz é uma matriz retangular de números dispostos em linhas e colunas.

MATRIZ

Uma matriz é uma matriz retangular de números dispostos em linhas e colunas.

Uma matriz com m linhas e n colunas tem ordem$m\times n$. A matriz à esquerda abaixo tem 2 linhas e 3 colunas e, portanto, tem ordem$2\times 3$. Dizemos que é uma matriz de 2 por 3.

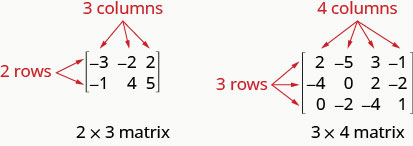
$A figura mostra duas matrizes. O da esquerda tem os números menos 3, menos 2 e 2 na primeira linha e os números menos 1, 4 e 5 na segunda linha. As linhas e colunas estão entre colchetes. Assim, ele tem 2 linhas e 3 colunas. É rotulado como matriz 2 cruzes 3 ou 2 por 3. A matriz à direita é semelhante, mas com 3 linhas e 4 colunas. É rotulado como matriz 3 por 4.$

Cada número na matriz é chamado de elemento ou entrada na matriz.

Usaremos uma matriz para representar um sistema de equações lineares. Escrevemos cada equação na forma padrão e os coeficientes das variáveis e a constante de cada equação se torna uma linha na matriz. Cada coluna então seria o coeficiente de uma das variáveis do sistema ou das constantes. Uma linha vertical substitui os sinais de igualdade. Chamamos a matriz resultante de matriz aumentada para o sistema de equações.

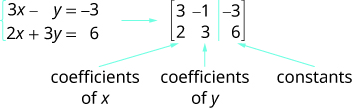
$As equações são 3x mais y é igual a menos 3 e 2x mais 3y é igual a 6. Uma matriz 2 por 3 é mostrada. A primeira linha é 3, 1, menos 3. A segunda linha é 2, 3, 6. A primeira coluna é rotulada como coeficientes de x. A segunda coluna é rotulada como coeficientes de y e a terceira é rotulada como constantes.$

Observe que a primeira coluna é composta por todos os coeficientes de x, a segunda coluna contém todos os coeficientes de y e a terceira coluna contém todas as constantes.

Exemplo$\PageIndex{1}$

ⓐ$\left\{ \begin{array} {l} 5x−3y=−1 \\ y=2x−2 \end{array} \right. $ ⓑ$ \left\{ \begin{array} {l} 6x−5y+2z=3 \\ 2x+y−4z=5 \\ 3x−3y+z=−1 \end{array} \right. $

Responda

ⓐ A segunda equação não está na forma padrão. Nós reescrevemos a segunda equação na forma padrão.

\[\begin{aligned} y=2x−2 \\ −2x+y=−2 \end{aligned} \nonumber\]

Substituímos a segunda equação por sua forma padrão. Na matriz aumentada, a primeira equação nos dá a primeira linha e a segunda equação nos dá a segunda linha. A linha vertical substitui os sinais de igualdade.

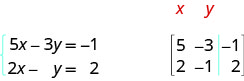
ⓑ Todas as três equações estão na forma padrão. Na matriz aumentada, a primeira equação nos dá a primeira linha, a segunda equação nos dá a segunda linha e a terceira equação nos dá a terceira linha. A linha vertical substitui os sinais de igualdade.

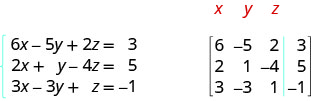
$As equações são 6x menos 5y mais 2z é igual a 3, 2x mais y menos 4z é igual a 5 e 3x menos 3y mais z é igual a menos 1. É mostrada uma matriz 4 por 3 cuja primeira linha é 6, menos 5, 2, 3. Sua segunda linha é 2, 1, menos 4, 5. Sua terceira linha é 3, menos 3, 1 e menos 1. Suas três primeiras colunas são rotuladas como x, y e z, respectivamente.$

Exemplo$\PageIndex{2}$

Escreva cada sistema de equações lineares como uma matriz aumentada:

ⓐ$\left\{ \begin{array} {l} 3x+8y=−3 \\ 2x=−5y−3 \end{array} \right. $ ⓑ$\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. $

Resposta

ⓐ$\left[ \begin{matrix} 3 &8 &-3 \\ 2 &5 &−3 \end{matrix} \right] $

ⓑ$\left[ \begin{matrix} 2 &3 &1 &−5 \\ −1 &3 &3 &4 \\ 2 &8 &7 &−3 \end{matrix} \right] $

Exemplo$\PageIndex{3}$

Escreva cada sistema de equações lineares como uma matriz aumentada:

ⓐ$\left\{ \begin{array} {l} 11x=−9y−5 \\ 7x+5y=−1 \end{array} \right. $ ⓑ$\left\{ \begin{array} {l} 5x−3y+2z=−5 \\ 2x−y−z=4 \\ 3x−2y+2z=−7 \end{array} \right. $

Resposta: ⓐ$\left[ \begin{matrix} 11 &9 &−5 \\ 7 &5 &−1 \end{matrix} \right] $
ⓑ$\left[ \begin{matrix} 5 &−3 &2 &−5 \\ 2 &−1 &−1 &4 \\ 3 &−2 &2 &−7 \end{matrix} \right] $

Ao resolvermos sistemas de equações usando matrizes, é importante poder ir e voltar entre o sistema e a matriz. O próximo exemplo nos pede que peguemos as informações na matriz e escrevamos o sistema de equações.

Exemplo$\PageIndex{4}$

Escreva o sistema de equações que corresponde à matriz aumentada:

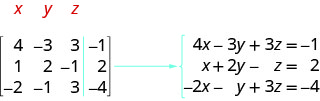
$\left[ \begin{array} {ccc|c} 4 &−3 &3 &−1 \\ 1 &2 &−1 &2 \\ −2 &−1 &3 &−4 \end{array} \right] $.

Resposta

Lembramos que cada linha corresponde a uma equação e que cada entrada é um coeficiente de uma variável ou constante. A linha vertical substitui o sinal de igual. Como essa matriz é a$4\times 3$, sabemos que ela se traduzirá em um sistema de três equações com três variáveis.

$Uma matriz de 3 por 4 é mostrada. Sua primeira linha é 4, menos 3, 3, menos 1. Sua segunda linha é 1, 2, menos 1, 2. Sua terceira linha é menos 2, menos 1, 3, menos 4. As três equações são 4x menos 3y mais 3z é igual a menos 1, x mais 2y menos z é igual a 2 e menos 2x menos y mais 3z é igual a menos 4.$

Exemplo$\PageIndex{5}$

Escreva o sistema de equações que corresponde à matriz aumentada:$\left[ \begin{matrix} 1 &−1 &2 &3 \\ 2 &1 &−2 &1 \\ 4 &−1 &2 &0 \end{matrix} \right] $.

Resposta: $\left\{ \begin{array} {l} x−y+2z=3 \\ 2x+y−2z=1 \\ 4x−y+2z=0 \end{array} \right.$

Exemplo$\PageIndex{6}$

Escreva o sistema de equações que corresponde à matriz aumentada:$\left[ \begin{matrix} 1 &1 &1 &4 \\ 2 &3 &−1 &8 \\ 1 &1 &−1 &3 \end{matrix} \right] $.

Resposta: $\left\{ \begin{array} {l} x+y+z=4 \\ 2x+3y−z=8 \\ x+y−z=3 \end{array} \right.$

Use operações de linha em uma matriz

Quando um sistema de equações estiver em sua forma de matriz aumentada, realizaremos operações nas linhas que nos levarão à solução.

Para resolver por eliminação, não importa em que ordem colocamos as equações no sistema. Da mesma forma, na matriz, podemos trocar as linhas.

Quando resolvemos por eliminação, geralmente multiplicamos uma das equações por uma constante. Como cada linha representa uma equação e podemos multiplicar cada lado de uma equação por uma constante, da mesma forma, podemos multiplicar cada entrada em uma linha por qualquer número real, exceto 0.

Na eliminação, geralmente adicionamos um múltiplo de uma linha a outra linha. Na matriz, podemos substituir uma linha por sua soma por um múltiplo de outra linha.

Essas ações são chamadas de operações de linha e nos ajudarão a usar a matriz para resolver um sistema de equações.

OPERAÇÕES DE LINHA

Em uma matriz, as seguintes operações podem ser executadas em qualquer linha e a matriz resultante será equivalente à matriz original.

Troque quaisquer duas linhas.
Multiplique uma linha por qualquer número real, exceto 0.
Adicione um múltiplo diferente de zero de uma linha a outra linha.

É fácil realizar essas operações, mas toda a aritmética pode resultar em um erro. Se usarmos um sistema para registrar a operação da linha em cada etapa, é muito mais fácil voltar e verificar nosso trabalho.

Usamos letras maiúsculas com assinaturas para representar cada linha. Em seguida, mostramos a operação à esquerda da nova matriz. Para mostrar a troca de uma linha:

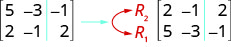
$Uma matriz 2 por 3 é mostrada. Sua primeira linha, chamada R2, é 2, menos 1, 2. Sua segunda linha, chamada R1, é 5, menos 3, menos 1.$

Para multiplicar a linha 2 por$−3$:

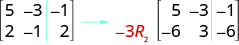
$Uma matriz 2 por 3 é mostrada. Sua primeira linha é 5, menos 3, menos 1. Sua segunda linha é 2, menos 1, 2. Uma seta aponta dessa matriz para outra à direita. A primeira linha da nova matriz é a mesma. A segunda linha é precedida por menos 3 R2. É menos 6, 3, menos 6.$

Para multiplicar a linha 2 por$−3$ e adicioná-la à linha 1:

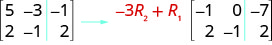
$Uma matriz 2 por 3 é mostrada. Sua primeira linha é 5, menos 3, menos 1. Sua segunda linha é 2, menos 1, 2. Uma seta aponta dessa matriz para outra à direita. A primeira linha da nova matriz é precedida por menos 3 R2 mais R1. É menos 1, 0, menos 7. A segunda linha é 2, menos 1, 2.$

Exemplo$\PageIndex{7}$

Execute as operações indicadas na matriz aumentada:

ⓐ Troque as linhas 2 e 3.

ⓑ Multiplique a linha 2 por 5.

$ \left[ \begin{array} {ccc|c} 6 &−5 &2 &3 \\ 2 &1 &−4 &5 \\ 3 &−3 &1 &−1 \end{array} \right] $

Resposta

ⓐ Nós trocamos as linhas 2 e 3.

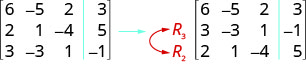
$Duas matrizes de 3 por 4 são mostradas. Na da esquerda, a primeira linha é 6, menos 5, 2, 3. A segunda linha é 2, 1, menos 4, 5. A terceira linha é 3, menos 3, 1, menos 1. A segunda matriz é semelhante, exceto que as linhas 2 e 3 são trocadas.$

ⓑ Multiplicamos a linha 2 por 5.

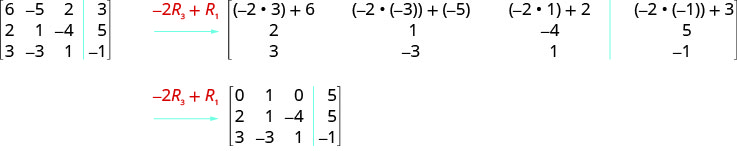
$Na matriz 3 por 4, a primeira linha é 6, menos 5, 2, 3. A segunda linha é 2, 1, menos 4, 5. A terceira linha é 3, menos 3, 1, menos 1. Executando a operação menos 2 R3 mais R1 na primeira linha, a primeira linha se torna 6 mais menos 2 vezes 3, menos 5 mais menos 2 vezes menos 3, 2 mais menos 2 vezes 1 e 3 mais menos 2 vezes menos 1. Isso se torna 0, 1, 0, 5. As 2 linhas restantes da nova matriz são as mesmas.$

Exemplo$\PageIndex{8}$

Execute as operações indicadas na matriz aumentada:

ⓐ Troque as linhas 1 e 3.

ⓑ Multiplique a linha 3 por 3.

$ \left[ \begin{array} {ccc|c} 5 &−2 &-2 &-2 \\ 4 &-1 &−4 &4 \\ -2 &3 &0 &−1 \end{array} \right] $

Resposta

ⓐ$ \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 5 &−2 &−2 &−2 \end{matrix} \right] $

ⓑ$ \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 15 &−6 &−6 &−6 \end{matrix} \right] $

ⓒ$ \left[ \begin{matrix} -2 &3 &0 &2 & \\ 3 &4 &-13 &-16 &-8 \\ 15 &-6 &-6 &-6 & \end{matrix} \right] $

Exemplo$\PageIndex{9}$

Execute as operações indicadas na matriz aumentada:

ⓐ Troque as linhas 1 e 2,

ⓑ Multiplique a linha 1 por 2,

$ \left[ \begin{array} {ccc|c} 2 &−3 &−2 &−4 \\ 4 &1 &−3 &2 \\ 5 &0 &4 &−1 \end{array} \right] $

Resposta: ⓐ$ \left[ \begin{matrix} 4 &1 &−3 &2 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] $
ⓑ$ \left[ \begin{matrix} 8 &2 &−6 &4 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] $
ⓒ$ \left[ \begin{matrix} 14 &−7 &−12 &−8 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] $

Agora que praticamos as operações de linha, examinaremos uma matriz aumentada e descobriremos qual operação usaremos para atingir uma meta. Isso é exatamente o que fizemos quando fizemos a eliminação. Decidimos por qual número multiplicar uma linha para que uma variável fosse eliminada ao somarmos as linhas.

Dado esse sistema, o que você faria para eliminar x?

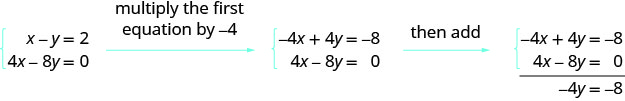
$As duas equações são x menos y é igual a 2 e 4x menos 8y é igual a 0. Multiplicando o primeiro por menos 4, obtemos menos 4x mais 4y é igual a menos 8. Somando isso à segunda equação, obtemos menos 4y igual a menos 8.$

O próximo exemplo basicamente faz a mesma coisa, mas com a matriz.

Exemplo$\PageIndex{10}$

Execute a operação de linha necessária que fará com que a primeira entrada na linha 2 seja zero na matriz aumentada:$ \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 4 &−8 &0 \end{array} \right] $

Resposta

Para tornar o 4 um 0, poderíamos multiplicar a linha 1 por$−4$ e depois adicioná-la à linha 2.

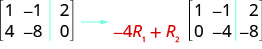
$A matriz 2 por 3 é 1, menos 1, 2 e 4, menos 8, 0. Executando a operação menos 4R1 mais R2 na linha 2, a segunda linha da nova matriz se torna 0, menos 4, menos 8. A primeira linha continua a mesma.$

Exemplo$\PageIndex{11}$

Execute a operação de linha necessária que fará com que a primeira entrada na linha 2 seja zero na matriz aumentada:$ \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 3 &−6 &2 \end{array} \right] $

Resposta: $ \left[ \begin{matrix} 1 &−1 &2 \\ 0 &−3 &−4 \end{matrix} \right] $

Exemplo$\PageIndex{12}$

Execute a operação de linha necessária que fará com que a primeira entrada na linha 2 seja zero na matriz aumentada:$ \left[ \begin{array} {cc|c} 1 &−1 &3 \\ -2 &−3 &2 \end{array} \right] $

Resposta: $ \left[ \begin{matrix} 1 &−1 &3 \\ 0 &−5 &8 \end{matrix} \right] $

Resolva sistemas de equações usando matrizes

Para resolver um sistema de equações usando matrizes, transformamos a matriz aumentada em uma matriz na forma escalonada de linha usando operações de linha. Para um sistema de equações consistente e independente, sua matriz aumentada está na forma escalonada quando, à esquerda da linha vertical, cada entrada na diagonal é 1 e todas as entradas abaixo da diagonal são zeros.

FORMULÁRIO DE ESCALÃO DE LINHA

Para um sistema de equações consistente e independente, sua matriz aumentada está na forma escalonada quando, à esquerda da linha vertical, cada entrada na diagonal é 1 e todas as entradas abaixo da diagonal são zeros.

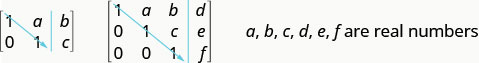
$Uma matriz 2 por 3 é mostrada à esquerda. Sua primeira linha é 1, a, b. A segunda linha é 0, 1, c. Uma seta aponta diagonalmente para baixo e para a direita, sobrepondo os 1s na matriz. Uma matriz de 3 por 4 é mostrada à direita. Sua primeira linha é 1, a, b, d. Sua segunda linha é 0, 1, c, e. Sua terceira linha é 0, 0, 1, f. Uma seta aponta diagonalmente para baixo e para a direita, sobrepondo todos os 1s na matriz. a, b, c, d, e, f são números reais.$

Depois de obtermos a matriz aumentada em forma de escalão de linha, podemos escrever o sistema equivalente de equações e ler o valor de pelo menos uma variável. Em seguida, substituímos esse valor em outra equação para continuar resolvendo as outras variáveis. Esse processo é ilustrado no próximo exemplo.

Como resolver um sistema de equações usando uma matriz

Resolva o sistema de equações usando uma matriz:$\left\{ \begin{array} {l} 3x+4y=5 \\ x+2y=1 \end{array} \right. $

Resposta: $As equações são 3x mais 4y é igual a 5 e x mais 2y é igual a 1. Etapa 1. Escreva a matriz aumentada para o sistema de equações. Obtemos uma matriz 2 por 3 com a primeira linha 3, 4, 5 e a segunda linha 1, 2, 1.$ $Etapa 2. Usando operações de linha, faça com que a entrada na linha 1, a coluna 1 seja 1. Troque as linhas R1 e R2.$ $Etapa 3. Usando operações de linha, obtenha zeros na coluna 1 abaixo do 1. Multiplique a linha 1 por menos 3 e adicione-a à linha 2. A linha 2 se torna 0, menos 2, 2.$ $Etapa 4. Usando operações de linha, faça com que a entrada na linha 2, coluna 2 seja 1. Multiplique a linha 2 por menos metade. A linha 2 se torna 0, 1, menos 1.$ $Etapa 5. Continue o processo até que a matriz esteja em forma de escalão de linha. A matriz agora está em forma de escalão de linha.$ $Etapa 6. Escreva o sistema de equações correspondente. Obtemos x mais 2y é igual a 1 e y é igual a menos 1.$ $Etapa 7. Use a substituição para encontrar as variáveis restantes. Substitua y igual a menos 1 em x mais 2y é igual a 1. X mais 2 vezes menos 1 é igual a 1. X menos 2 é igual a 1. Obtemos x igual a 3.$ $Etapa 8. Escreva a solução como um par ordenado ou triplo. O par ordenado é (3, menos 1).$ $Etapa 9. Verifique se a solução torna as equações originais verdadeiras.$

Exemplo$\PageIndex{14}$

Resolva o sistema de equações usando uma matriz:$\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. $

Resposta: A solução é$(4,−1)$.

Exemplo$\PageIndex{15}$

Resolva o sistema de equações usando uma matriz:$\left\{ \begin{array} {l} 2x+y=−4 \\ x−y=−2 \end{array} \right. $

Resposta: A solução é$(−2,0)$.

As etapas estão resumidas aqui.

RESOLVA UM SISTEMA DE EQUAÇÕES USANDO MATRIZES.

Escreva a matriz aumentada para o sistema de equações.
Usando operações de linha, faça com que a entrada na linha 1, a coluna 1 seja 1.
Usando operações de linha, obtenha zeros na coluna 1 abaixo do 1.
Usando operações de linha, faça com que a entrada na linha 2, coluna 2 seja 1.
Continue o processo até que a matriz esteja em forma de escalão de linha.
Escreva o sistema de equações correspondente.
Use a substituição para encontrar as variáveis restantes.
Escreva a solução como um par ordenado ou triplo.
Verifique se a solução torna as equações originais verdadeiras.

Aqui está um visual para mostrar a ordem para obter os 1 e 0 na posição correta para a forma escalonada de linha.

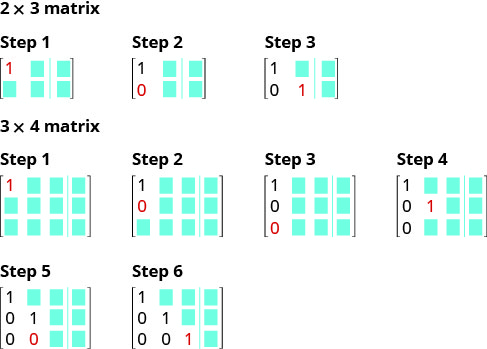
$A figura mostra 3 etapas para uma matriz 2 por 3 e 6 etapas para uma matriz 3 por 4. Para a primeira, a etapa 1 é obter um 1 na linha 1 coluna 1. O passo a passo é obter um 0 é a linha 2 coluna 1. A etapa 3 é obter um 1 na linha 2 coluna 2. Para uma matriz 3 por 4, a etapa 1 é obter um 1 na linha 1 coluna 1. A etapa 2 é obter um 0 na linha 2, coluna 1. A etapa 3 é obter um 0 na linha 3 coluna 1. A etapa 4 é obter um 1 na linha 2 coluna 2. A etapa 5 é obter um 0 na linha 3 coluna 2. A etapa 6 é obter um 1 na linha 3 coluna 3.$

Usamos o mesmo procedimento quando o sistema de equações tem três equações.

Exemplo$\PageIndex{16}$

Resolva o sistema de equações usando uma matriz:$\left\{ \begin{array} {l} 3x+8y+2z=−5 \\ 2x+5y−3z=0 \\ x+2y−2z=−1 \end{array} \right. $

Resposta

	$.$
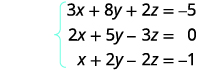
Escreva a matriz aumentada para as equações.	$.$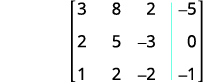
Troque as linhas 1 e 3 para obter a entrada na linha 1, a coluna 1 para ser 1.	$.$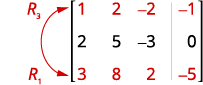
Usando operações de linha, obtenha zeros na coluna 1 abaixo do 1.	$.$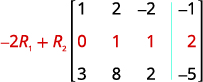
	$.$
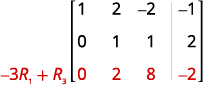
A entrada na linha 2, coluna 2, agora é 1.
Continue o processo até que a matriz esteja em forma de escalão de linha.	$.$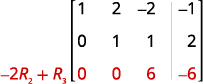
	$.$
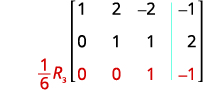
A matriz agora está em forma de escalão de linha.	$.$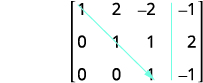
Escreva o sistema de equações correspondente.	$.$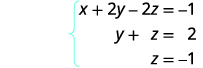
Use a substituição para encontrar as variáveis restantes.	$.$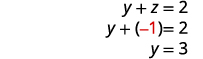
	$.$ $.$
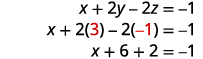
Escreva a solução como um par ordenado ou triplo.	$.$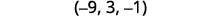
Verifique se a solução torna as equações originais verdadeiras.	Deixamos o cheque para você.

Exemplo$\PageIndex{17}$

Resolva o sistema de equações usando uma matriz:$\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. $

Resposta: $(6,−1,−3)$

Exemplo$\PageIndex{18}$

Resolva o sistema de equações usando uma matriz:$\left\{ \begin{array} {l} −3x+y+z=−4 \\ −x+2y−2z=1 \\ 2x−y−z=−1 \end{array} \right. $

Resposta: $(5,7,4)$

Até agora, nosso trabalho com matrizes tem sido apenas com sistemas consistentes e independentes, o que significa que eles têm exatamente uma solução. Vamos agora ver o que acontece quando usamos uma matriz para um sistema dependente ou inconsistente.

Exemplo$\PageIndex{19}$

Resolva o sistema de equações usando uma matriz:$\left\{ \begin{array} {l} x+y+3z=0 \\ x+3y+5z=0 \\ 2x+4z=1 \end{array} \right. $

Resposta

	$.$
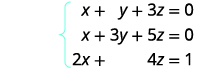
Escreva a matriz aumentada para as equações.	$.$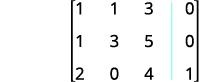
A entrada na linha 1, coluna 1 é 1.
Usando operações de linha, obtenha zeros na coluna 1 abaixo do 1.	$.$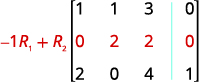
	$.$
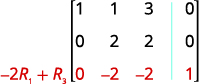
Continue o processo até que a matriz esteja em forma de escalão de linha.	$.$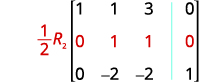
Multiplique a linha 2 por 2 e adicione-a à linha 3.	$.$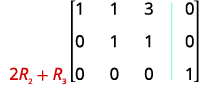
Neste ponto, temos todos os zeros à esquerda da linha 3.
Escreva o sistema de equações correspondente.	$.$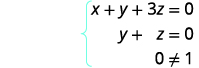
Já que$0 \neq 1 $ temos uma declaração falsa. Assim como quando resolvemos um sistema usando outros métodos, isso nos diz que temos um sistema inconsistente. Não há solução.

Exemplo$\PageIndex{20}$

Resolva o sistema de equações usando uma matriz:$\left\{ \begin{array} {l} x−2y+2z=1 \\ −2x+y−z=2 \\ x−y+z=5 \end{array} \right. $

Resposta: sem solução

Exemplo$\PageIndex{21}$

Resolva o sistema de equações usando uma matriz:$\left\{ \begin{array} {l} 3x+4y−3z=−2 \\ −2x+3y−z=−1 \\ 2x+y−2z=6 \end{array} \right. $

Resposta: sem solução

O último sistema era inconsistente e, portanto, não tinha soluções. O próximo exemplo é dependente e tem infinitas soluções.

Exemplo$\PageIndex{22}$

Resolva o sistema de equações usando uma matriz:$\left\{ \begin{array} {l} x−2y+3z=1 \\ x+y−3z=7 \\ 3x−4y+5z=7 \end{array} \right. $

Resposta

	$.$
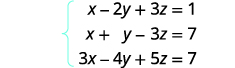
Escreva a matriz aumentada para as equações.	$.$
A entrada na linha 1, coluna 1 é 1.
Usando operações de linha, obtenha zeros na coluna 1 abaixo do 1.	$.$
	$.$
Continue o processo até que a matriz esteja em forma de escalão de linha.	$.$
Multiplique a linha 2 por$−2$ e adicione-a à linha 3.	$.$
Neste ponto, temos todos os zeros na linha inferior.
Escreva o sistema de equações correspondente.	$.$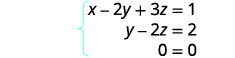
Já$0=0$ que temos uma declaração verdadeira. Assim como quando resolvemos por substituição, isso nos diz que temos um sistema dependente. Existem infinitas soluções.
Resolva y em termos de z na segunda equação.	$.$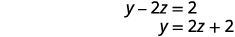
Resolva a primeira equação para x em termos de z.	$.$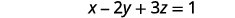
Substituto$y=2z+2$.	$.$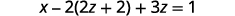
Simplifique.	$.$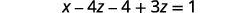
Simplifique.	$.$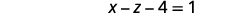
Simplifique.	$.$
O sistema tem infinitas soluções$(x,y,z)$, onde$x=z+5;\space y=2z+2;\space z$ está qualquer número real.

Exemplo$\PageIndex{23}$

Resolva o sistema de equações usando uma matriz:$\left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. $

Resposta: infinitas soluções$(x,y,z)$, onde$x=z−3;\space y=3;\space z$ está qualquer número real.

Exemplo$\PageIndex{24}$

Resolva o sistema de equações usando uma matriz:$\left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. $

Resposta: infinitas soluções$(x,y,z)$, onde$x=5z−2;\space y=4z−3;\space z$ está qualquer número real.

Acesse este recurso on-line para obter instruções e práticas adicionais com a eliminação gaussiana.

Eliminação gaussiana

Conceitos-chave

Matriz: Uma matriz é uma matriz retangular de números dispostos em linhas e colunas. Uma matriz com m linhas e n colunas tem ordem$m\times n$. A matriz à esquerda abaixo tem 2 linhas e 3 colunas e, portanto, tem ordem$2\times 3$. Dizemos que é uma matriz de 2 por 3.
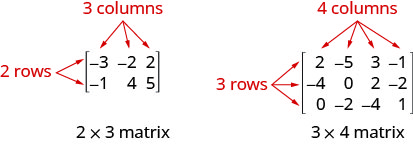
$A figura mostra duas matrizes. O da esquerda tem os números menos 3, menos 2 e 2 na primeira linha e os números menos 1, 4 e 5 na segunda linha. As linhas e colunas estão entre colchetes. Assim, ele tem 2 linhas e 3 colunas. É rotulado como matriz 2 cruzes 3 ou 2 por 3. A matriz à direita é semelhante, mas com 3 linhas e 4 colunas. É rotulado como matriz 3 por 4.$
Cada número na matriz é chamado de elemento ou entrada na matriz.
Operações de linha: Em uma matriz, as seguintes operações podem ser realizadas em qualquer linha e a matriz resultante será equivalente à matriz original.
- Troque quaisquer duas linhas
- Multiplique uma linha por qualquer número real, exceto 0
- Adicionar um múltiplo diferente de zero de uma linha a outra linha
Forma escalonada de linha: Para um sistema de equações consistente e independente, sua matriz aumentada está na forma escalonada de linha quando, à esquerda da linha vertical, cada entrada na diagonal é 1 e todas as entradas abaixo da diagonal são zeros.
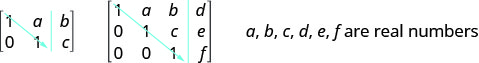
$A figura mostra duas matrizes. O da esquerda tem os números menos 3, menos 2 e 2 na primeira linha e os números menos 1, 4 e 5 na segunda linha. As linhas e colunas estão entre colchetes. Assim, ele tem 2 linhas e 3 colunas. É rotulado como matriz 2 cruzes 3 ou 2 por 3. A matriz à direita é semelhante, mas com 3 linhas e 4 colunas. É rotulado como matriz 3 por 4.$
Como resolver um sistema de equações usando matrizes.
1. Escreva a matriz aumentada para o sistema de equações.
2. Usando operações de linha, faça com que a entrada na linha 1, a coluna 1 seja 1.
3. Usando operações de linha, obtenha zeros na coluna 1 abaixo do 1.
4. Usando operações de linha, faça com que a entrada na linha 2, coluna 2 seja 1.
5. Continue o processo até que a matriz esteja em forma de escalão de linha.
6. Escreva o sistema de equações correspondente.
7. Use a substituição para encontrar as variáveis restantes.
8. Escreva a solução como um par ordenado ou triplo.
9. Verifique se a solução torna as equações originais verdadeiras.

Glossário

matriz: Uma matriz é uma matriz retangular de números dispostos em linhas e colunas.

forma de escalão de linha: Uma matriz está na forma escalonada de linha quando, à esquerda da linha vertical, cada entrada na diagonal é 1 e todas as entradas abaixo da diagonal são zeros.

MATRIZ

Exemplo\(\PageIndex{1}\)

Exemplo\(\PageIndex{2}\)

Exemplo\(\PageIndex{3}\)

Exemplo\(\PageIndex{4}\)

Exemplo\(\PageIndex{5}\)

Exemplo\(\PageIndex{6}\)

OPERAÇÕES DE LINHA

Exemplo\(\PageIndex{7}\)

Exemplo\(\PageIndex{8}\)

Exemplo\(\PageIndex{9}\)

Exemplo\(\PageIndex{10}\)

Exemplo\(\PageIndex{11}\)

Exemplo\(\PageIndex{12}\)

FORMULÁRIO DE ESCALÃO DE LINHA

Como resolver um sistema de equações usando uma matriz

Exemplo\(\PageIndex{14}\)

Exemplo\(\PageIndex{15}\)

RESOLVA UM SISTEMA DE EQUAÇÕES USANDO MATRIZES.

Exemplo\(\PageIndex{16}\)

Exemplo\(\PageIndex{17}\)

Exemplo\(\PageIndex{18}\)

Exemplo\(\PageIndex{19}\)

Exemplo\(\PageIndex{20}\)

Exemplo\(\PageIndex{21}\)

Exemplo\(\PageIndex{22}\)

Exemplo\(\PageIndex{23}\)

Exemplo\(\PageIndex{24}\)